6.1 第4课时 组内离差平方和 课件(共27张PPT) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 6.1 第4课时 组内离差平方和 课件(共27张PPT) 2025-2026学年数学北师大版(2024)八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 23:36:39 | ||
图片预览






文档简介
(共27张PPT)
第4课时 组内离差平方和
第六章 数据的分析
1.平均数与方差
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
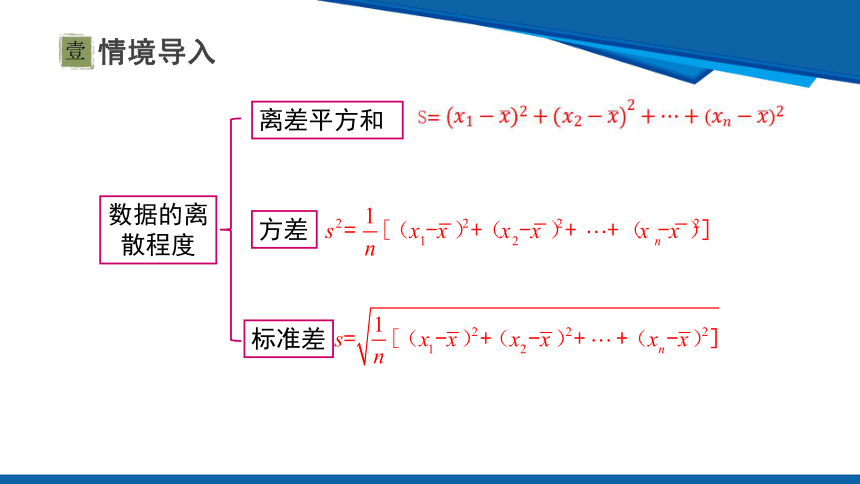
数据的离散程度
离差平方和
方差
标准差
叁
肆
叁
壹
新知初探
贰
新知初探
探究一:方差的应用
贰
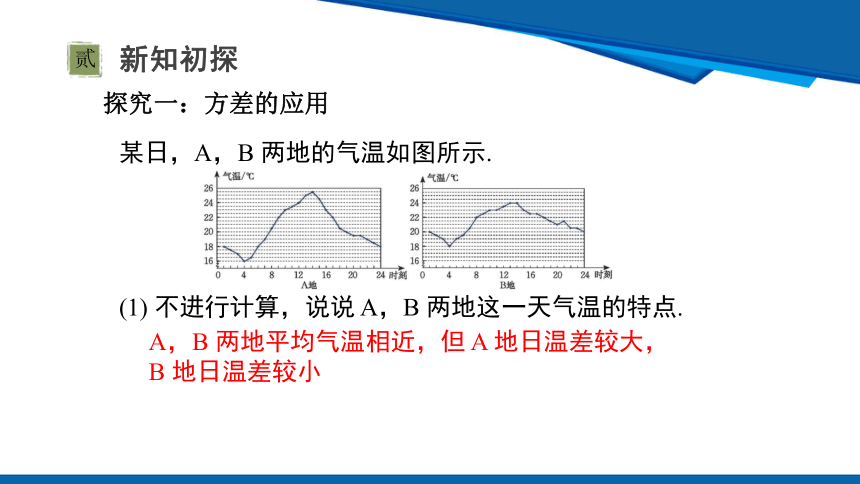
某日,A,B 两地的气温如图所示.
(1) 不进行计算,说说 A,B 两地这一天气温的特点.
A,B 两地平均气温相近,但 A 地日温差较大,B 地日温差较小
新知初探
贰
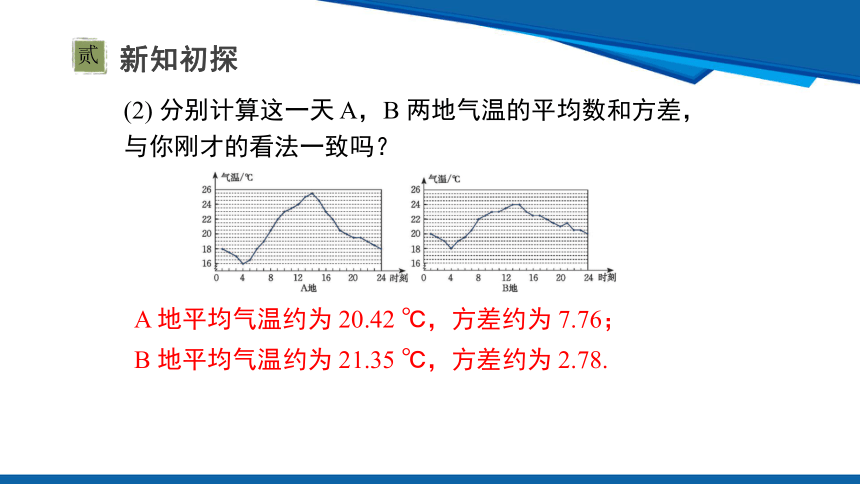
(2) 分别计算这一天 A,B 两地气温的平均数和方差,与你刚才的看法一致吗?
A 地平均气温约为 20.42 ℃,方差约为 7.76;
B 地平均气温约为 21.35 ℃,方差约为 2.78.
新知初探
贰
某校要从甲、乙两个跳远运动员中挑选一人参加一项比赛. 在最近的 10 次选拔赛中,他们的成绩 (单位:cm) 如下:
甲:585, 596, 610, 598, 612, 597, 604, 600, 613, 601;
乙:613, 618, 580, 574, 618, 593, 585, 590, 598, 624.
(1) 甲、乙的平均成绩分别是多少?
尝试思考
甲:(585+596+610+598+612+597+604+600+613+601)÷10
= 601.6 cm
乙:(613+618+580+574+618+593+585+590+598+624)÷10
= 599.3 cm
新知初探
贰
(2) 甲、乙这 10 次比赛成绩的方差分别是多少?
(3) 这两名运动员的运动成绩各有什么特点?
S甲2 = 65.84
S乙2 = 284.21
甲运动员成绩较稳定,因为其方差比较小;
还可以说乙较有潜质,因为乙的最远成绩比甲的最远成绩好等. (答案不唯一,合理即可)
新知初探
贰
(4) 历届比赛成绩表明,成绩达到 5.96 m 就很可能夺冠,你认为为了夺冠应选谁参加这项比赛?如果历届比赛成绩表明,成绩达到 6.10 m 就能打破纪录,那么你认为为了打破纪录应选谁参加这项比赛呢?
在 10 次比赛中,甲运动员有 9 次超过 596 cm,而乙仅有 5 次,因此一般应选甲运动员参加这项比赛;
但若要打破 610 cm 的跳远纪录,则一般应选乙运动员.
新知初探
探究二:组内离差平方和
贰
尝试思考
10个苹果的直径如图6-6所示。
新知初探
贰
(2)一般情况下,如果想把一组数据分成若干组,使每组组内的数据差距不大,且组与组之间的数据差别明显,那么你认为应遵循怎样的分组原则 与同伴进行交流。
(1)若想把这10个苹果分成两组,使每组苹果的“个头”差不多,你想怎么分 说说你分组的理由。
问题:
新知初探
贰
在统计学里,分组的方法有很多,其中较常用的方法是使“组内离差平方和达到最小”。多组数据的组内离差平方和是指每组数据的离差平方和的和。
归纳总结
新知初探
贰
例3 按照“组内离差平方和达到最小”的方法,把图6-6中的10个苹果按直径大小分成两组。
典型例题
解:将10个数据由小到大排序:
65, 69, 70, 75, 76, 76, 78, 80, 80, 81。
把10个数据分成两组,共有9种情况:第一组1个数据{65},第二组9个数据{69, …, 81}; 第一组2个数据{65, 69}, 第二组8个数据{70, …,81}; ……; 第一组9个数据{65, …, 80}, 第二组1个数据{81}。
新知初探
贰
新知初探
贰
同理计算其他8种分组情况的组内离差平方和,结果如下:
分组情况 组内离差平方和
第一组1个,第二组9个 146.889
第一组2个,第二组8个 98
第一组3个,第二组7个 48
第一组4个,第二组6个 74.25
第一组5个,第二组5个 98
第一组6个,第二组4个 107.583
第一组7个,第二组3个 136.095
第一组8个,第二组2个 182.375
第一组9个第二组1个 218
计算结果表明,第3种情况的组内离差平方和最小。因此把10个苹果按直径大小分成的两组是{65, 69, 70}, {75, 76, 76, 78, 80, 80, 81}。
新知初探
贰
1.已知一组数据的方差为4,现将每个数据都加上3,则新数据的方差为( )
A. 1 B. 4 C. 7 D. 16
2.下列哪种情况适合使用组内离差平方和最小的原理?( )
A. 比较两种药物的疗效 B. 将学生按成绩分组
C. 分析股票价格波动 D. 预测天气变化
B
C
随堂练习
当堂达标
叁
当堂达标
叁
1. 若一组数据 x1 + 1,x2 + 1,…,xn + 1 的方差为 1,则另一组数据 x1 + 2,x2 + 2,…,xn + 2 的方差是
;数据 3x1 + 2,3x2 + 2,…,3xn + 2 的方差是 .
1
9
叁
肆
叁
叁
当堂达标
叁
2. 甲、乙两台编织机纺织一种毛衣,在 5 天中两台编织机每天出的合格品数如下(单位:件):
甲:7 10 8 8 7; 乙:8 9 7 9 7.
计算在这 5 天中,哪台编织机出合格品的波动较小?
解:
所以乙编织机出合格品的波动较小.
= (7 + 10 + 8 + 8 + 7)÷5 = 8,
= (8 + 9 + 7 + 9 + 7)÷5 = 8.
叁
肆
叁
叁
当堂达标
叁
3. 为了从甲、乙两名学生中选择一人去参加电脑知
识竞赛,在相同条件下对他们的电脑知识进行 10 次测验,成绩(单位:分)如下:
甲的成绩 76 84 90 84 81 87 88 81 85 84
乙的成绩 82 86 87 90 79 81 93 90 74 78
(1)填写下表:
同学 平均成绩 众数 方差 85 分以上的频率
甲 84 84 0.4
乙 84 34
90
0.5
14.4
叁
肆
叁
叁
当堂达标
叁
(2)利用以上信息,请从不同的角度对甲、乙两名同学的成绩进行评价.
解:从众数看,甲成绩的众数为 84 分,乙成绩的众数是 90 分,乙的成绩比甲好;
从甲、乙的平均数看,平均数都是 84 分,两人成绩一样好;
从方差看,s2甲 = 14.4,s2乙 = 34,甲的成绩比乙相对稳定;
从频率看,甲 85 分以上的次数比乙少,乙的成绩比甲好.
叁
肆
叁
叁
当堂达标
叁
4.为考查某品种小麦的长势,测量了8株麦苗的高(单位:cm),结果如下:21,21,22,23,23,24,25,25。
按照“组内离差平方和达到最小”的方法,把这8个数据分成两组。
叁
肆
叁
叁
当堂达标
叁
解:计算不同分组的组内离差平方和如下:
其中组内离差平方和最小的分组是{21,21,22},{23,23,24,25,25}和{21,21,22,23,23},{24,25,25}.
叁
肆
叁
叁
课堂小结
肆
课堂小结
肆
根据本节课的学习,说说你学会了什么?
我学会了利用组内离差平方和对数据进行分组.
我学会了计算平均数和方差,并合理利用数据分析作出决策.
叁
叁
肆
叁
肆
课后作业
基础题:1.课后习题 第 15,16,17题。
提高题:2.请学有余力的同学完成课后习题第18题
谢
谢
第4课时 组内离差平方和
第六章 数据的分析
1.平均数与方差
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
数据的离散程度
离差平方和
方差
标准差
叁
肆
叁
壹
新知初探
贰
新知初探
探究一:方差的应用
贰
某日,A,B 两地的气温如图所示.
(1) 不进行计算,说说 A,B 两地这一天气温的特点.
A,B 两地平均气温相近,但 A 地日温差较大,B 地日温差较小
新知初探
贰
(2) 分别计算这一天 A,B 两地气温的平均数和方差,与你刚才的看法一致吗?
A 地平均气温约为 20.42 ℃,方差约为 7.76;
B 地平均气温约为 21.35 ℃,方差约为 2.78.
新知初探
贰
某校要从甲、乙两个跳远运动员中挑选一人参加一项比赛. 在最近的 10 次选拔赛中,他们的成绩 (单位:cm) 如下:
甲:585, 596, 610, 598, 612, 597, 604, 600, 613, 601;
乙:613, 618, 580, 574, 618, 593, 585, 590, 598, 624.
(1) 甲、乙的平均成绩分别是多少?
尝试思考
甲:(585+596+610+598+612+597+604+600+613+601)÷10
= 601.6 cm
乙:(613+618+580+574+618+593+585+590+598+624)÷10
= 599.3 cm
新知初探
贰
(2) 甲、乙这 10 次比赛成绩的方差分别是多少?
(3) 这两名运动员的运动成绩各有什么特点?
S甲2 = 65.84
S乙2 = 284.21
甲运动员成绩较稳定,因为其方差比较小;
还可以说乙较有潜质,因为乙的最远成绩比甲的最远成绩好等. (答案不唯一,合理即可)
新知初探
贰
(4) 历届比赛成绩表明,成绩达到 5.96 m 就很可能夺冠,你认为为了夺冠应选谁参加这项比赛?如果历届比赛成绩表明,成绩达到 6.10 m 就能打破纪录,那么你认为为了打破纪录应选谁参加这项比赛呢?
在 10 次比赛中,甲运动员有 9 次超过 596 cm,而乙仅有 5 次,因此一般应选甲运动员参加这项比赛;
但若要打破 610 cm 的跳远纪录,则一般应选乙运动员.
新知初探
探究二:组内离差平方和
贰
尝试思考
10个苹果的直径如图6-6所示。
新知初探
贰
(2)一般情况下,如果想把一组数据分成若干组,使每组组内的数据差距不大,且组与组之间的数据差别明显,那么你认为应遵循怎样的分组原则 与同伴进行交流。
(1)若想把这10个苹果分成两组,使每组苹果的“个头”差不多,你想怎么分 说说你分组的理由。
问题:
新知初探
贰
在统计学里,分组的方法有很多,其中较常用的方法是使“组内离差平方和达到最小”。多组数据的组内离差平方和是指每组数据的离差平方和的和。
归纳总结
新知初探
贰
例3 按照“组内离差平方和达到最小”的方法,把图6-6中的10个苹果按直径大小分成两组。
典型例题
解:将10个数据由小到大排序:
65, 69, 70, 75, 76, 76, 78, 80, 80, 81。
把10个数据分成两组,共有9种情况:第一组1个数据{65},第二组9个数据{69, …, 81}; 第一组2个数据{65, 69}, 第二组8个数据{70, …,81}; ……; 第一组9个数据{65, …, 80}, 第二组1个数据{81}。
新知初探
贰
新知初探
贰
同理计算其他8种分组情况的组内离差平方和,结果如下:
分组情况 组内离差平方和
第一组1个,第二组9个 146.889
第一组2个,第二组8个 98
第一组3个,第二组7个 48
第一组4个,第二组6个 74.25
第一组5个,第二组5个 98
第一组6个,第二组4个 107.583
第一组7个,第二组3个 136.095
第一组8个,第二组2个 182.375
第一组9个第二组1个 218
计算结果表明,第3种情况的组内离差平方和最小。因此把10个苹果按直径大小分成的两组是{65, 69, 70}, {75, 76, 76, 78, 80, 80, 81}。
新知初探
贰
1.已知一组数据的方差为4,现将每个数据都加上3,则新数据的方差为( )
A. 1 B. 4 C. 7 D. 16
2.下列哪种情况适合使用组内离差平方和最小的原理?( )
A. 比较两种药物的疗效 B. 将学生按成绩分组
C. 分析股票价格波动 D. 预测天气变化
B
C
随堂练习
当堂达标
叁
当堂达标
叁
1. 若一组数据 x1 + 1,x2 + 1,…,xn + 1 的方差为 1,则另一组数据 x1 + 2,x2 + 2,…,xn + 2 的方差是
;数据 3x1 + 2,3x2 + 2,…,3xn + 2 的方差是 .
1
9
叁
肆
叁
叁
当堂达标
叁
2. 甲、乙两台编织机纺织一种毛衣,在 5 天中两台编织机每天出的合格品数如下(单位:件):
甲:7 10 8 8 7; 乙:8 9 7 9 7.
计算在这 5 天中,哪台编织机出合格品的波动较小?
解:
所以乙编织机出合格品的波动较小.
= (7 + 10 + 8 + 8 + 7)÷5 = 8,
= (8 + 9 + 7 + 9 + 7)÷5 = 8.
叁
肆
叁
叁
当堂达标
叁
3. 为了从甲、乙两名学生中选择一人去参加电脑知
识竞赛,在相同条件下对他们的电脑知识进行 10 次测验,成绩(单位:分)如下:
甲的成绩 76 84 90 84 81 87 88 81 85 84
乙的成绩 82 86 87 90 79 81 93 90 74 78
(1)填写下表:
同学 平均成绩 众数 方差 85 分以上的频率
甲 84 84 0.4
乙 84 34
90
0.5
14.4
叁
肆
叁
叁
当堂达标
叁
(2)利用以上信息,请从不同的角度对甲、乙两名同学的成绩进行评价.
解:从众数看,甲成绩的众数为 84 分,乙成绩的众数是 90 分,乙的成绩比甲好;
从甲、乙的平均数看,平均数都是 84 分,两人成绩一样好;
从方差看,s2甲 = 14.4,s2乙 = 34,甲的成绩比乙相对稳定;
从频率看,甲 85 分以上的次数比乙少,乙的成绩比甲好.
叁
肆
叁
叁
当堂达标
叁
4.为考查某品种小麦的长势,测量了8株麦苗的高(单位:cm),结果如下:21,21,22,23,23,24,25,25。
按照“组内离差平方和达到最小”的方法,把这8个数据分成两组。
叁
肆
叁
叁
当堂达标
叁
解:计算不同分组的组内离差平方和如下:
其中组内离差平方和最小的分组是{21,21,22},{23,23,24,25,25}和{21,21,22,23,23},{24,25,25}.
叁
肆
叁
叁
课堂小结
肆
课堂小结
肆
根据本节课的学习,说说你学会了什么?
我学会了利用组内离差平方和对数据进行分组.
我学会了计算平均数和方差,并合理利用数据分析作出决策.
叁
叁
肆
叁
肆
课后作业
基础题:1.课后习题 第 15,16,17题。
提高题:2.请学有余力的同学完成课后习题第18题
谢
谢
同课章节目录
