7.2 第1课时 平行线的判定 课件(共24张PPT) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 7.2 第1课时 平行线的判定 课件(共24张PPT) 2025-2026学年数学北师大版(2024)八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 23:39:32 | ||
图片预览




文档简介
(共24张PPT)
第1课时 平行线的判定
第七章 命题与证明
2.平行线的证明
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
据说,人类知识的 75% 是在操作中学到的.
小明用下面的方法作出平行线,你认为他的作法对吗?为什么?
同旁内角互补,两直线平行.
同位角相等,两直线平行.
内错角相等,两直线平行.
叁
叁
肆
叁
壹
情境导入
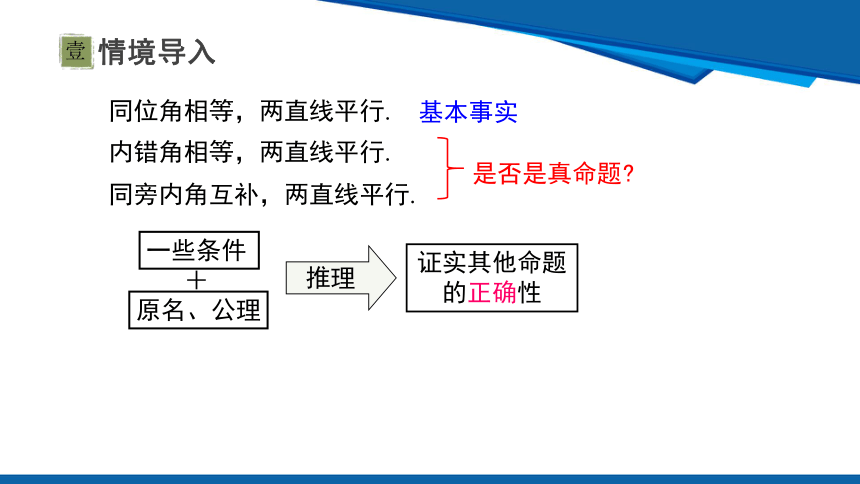
同旁内角互补,两直线平行.
同位角相等,两直线平行.
内错角相等,两直线平行.
基本事实
证实其他命题的正确性
推理
原名、公理
一些条件
+
是否是真命题
叁
叁
肆
叁
壹
新知初探
贰
新知初探
探究一:平行线的判定
贰
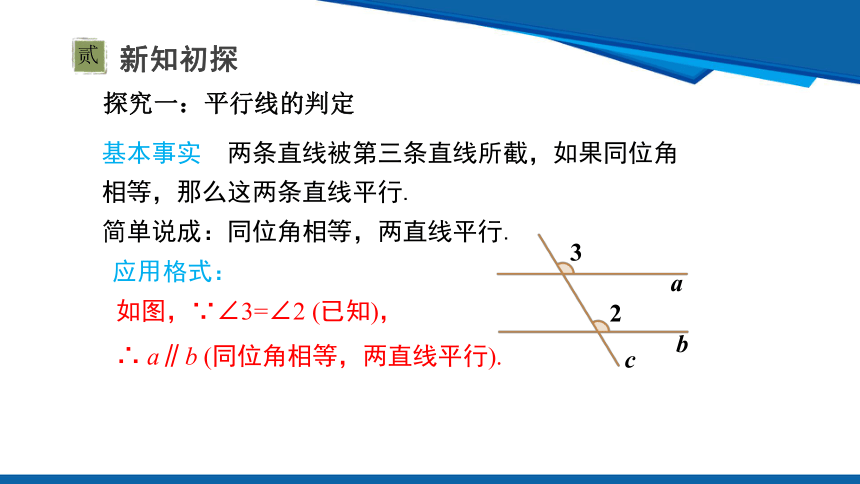
基本事实 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
如图,∵∠3=∠2 (已知),
∴ a∥b (同位角相等,两直线平行).
应用格式:
a
b
c
3
2
新知初探
贰
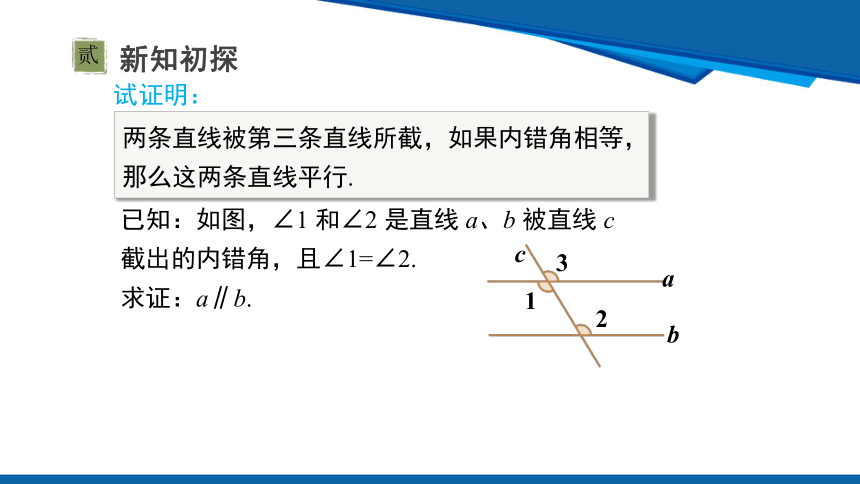
试证明:
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
已知:如图,∠1 和∠2 是直线 a、b 被直线 c 截出的内错角,且∠1=∠2.
求证:a∥b.
a
b
3
2
1
c
新知初探
贰
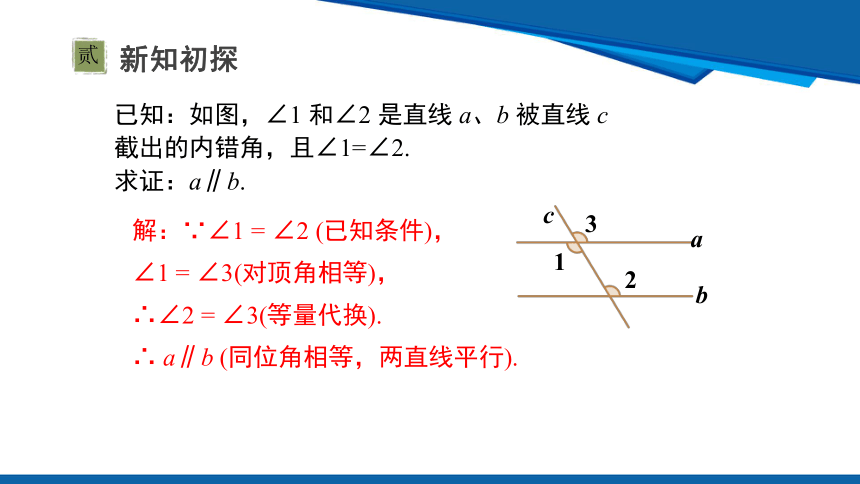
解:∵∠1 = ∠2 (已知条件),
∠1 = ∠3(对顶角相等),
∴∠2 = ∠3(等量代换).
∴ a∥b (同位角相等,两直线平行).
已知:如图,∠1 和∠2 是直线 a、b 被直线 c 截出的内错角,且∠1=∠2.
求证:a∥b.
a
b
3
2
1
c
新知初探
贰
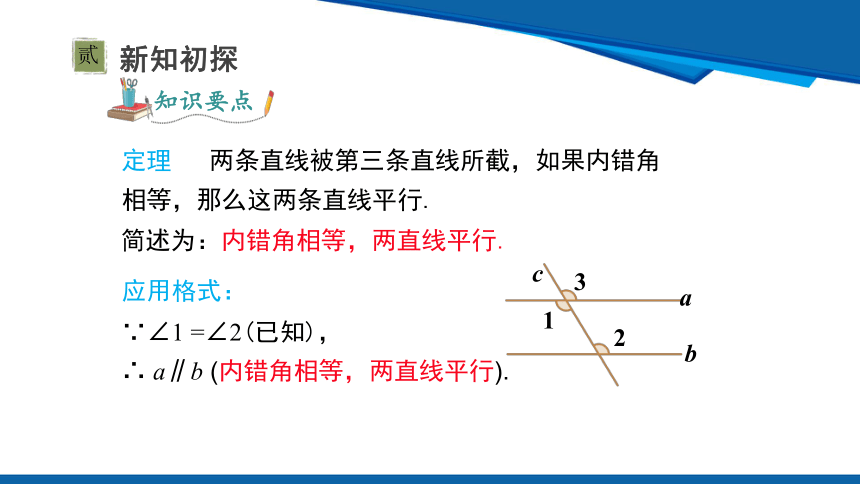
定理 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简述为:内错角相等,两直线平行.
∵∠1 =∠2(已知),
∴ a∥b (内错角相等,两直线平行).
应用格式:
知识要点
a
b
3
2
1
c
新知初探
贰
自主探究
试证明:
已知:如图,∠1 和∠2 是直线 a、b 被直线 c 截出的同旁内角,且∠1 与∠2 互补.
求证:a∥b.
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
a
b
3
2
1
c
新知初探
贰
证明:∵∠1 与∠2 互补 (已知),
∵∠3 +∠2 = 180° (补角的定义),
∴ ∠1=∠3 (等量代换).
∴ a∥b (同位角相等,两直线平行).
已知:如图,∠1 和∠2 是直线 a、b 被直线 c 截出的同旁内角,且∠1 与∠2 互补.
求证:a∥b.
a
b
3
2
1
c
∴ ∠1 +∠2 = 180° (互补的定义),
∴ ∠1 = 180°-∠2 (等式的性质).
∴∠3 = 180°-∠2 (等式的性质).
方法一
新知初探
贰
∵∠2+∠3=180°(补角的定义),
∴ ∠1=∠3(同角的补角相等).
∴ a∥b(内错角相等,两直线平行).
a
b
3
2
1
c
证明:∵∠1 与∠2 互补 (已知),
∴ ∠1 +∠2 = 180° (互补的定义),
已知:如图,∠1 和∠2 是直线 a、b 被直线 c 截出的同旁内角,且∠1 与∠2 互补.
求证:a∥b.
方法二
新知初探
贰
定理 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简述为:同旁内角互补,两直线平行.
∵∠1 +∠2 = 180°(已知),
∴ a∥b (同旁内角互补,两直线平行).
应用格式:
知识要点
a
b
3
2
1
c
新知初探
贰
① ∵∠1 =_____(已知),
∴ AB∥CE ( ).
② ∵∠1 +_____= 180°(已知),
∴ CD∥BF ( ).
③ ∵∠1 +∠5 = 180°(已知),
∴ _____∥_____ ( ).
CE
AB
∠2
④ ∵∠4 +_____= 180°(已知),
∴ AB∥CE ( ).
∠3
∠3
1
3
5
4
2
C
F
E
A
D
B
内错角相等,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
根据图形完成填空:
随堂练习
新知初探
探究二:平行线判定的应用
贰
(1)我们可以用如图的方法作出平行线,你能说说其中的道理吗
一、放
二、靠
三、推
四、画
内错角相等
两直线平行
(2)在一张不规则的四边形纸片上折出平行线,并予以证明,与同伴交流各自的折纸方法与证明过程
当堂达标
叁
当堂达标
叁
1. 对于图中标记的各角,下列条件能够推理得到 a∥b 的是 ( )
A.∠1 = ∠2 B.∠2 = ∠4
C.∠3 = ∠4 D.∠1 +∠4 = 180°
【解析】∠1 的对顶角与∠4 是同旁内角,若∠1 +∠4 = 180°,可以根据同旁内角互补,两直线平行得到 a∥b.
D
叁
叁
肆
叁
叁
当堂达标
叁
2. 如图.(1)从∠1 = ∠4,可以推出 ∥ ,
理由是 .
(2) 从∠ABC +∠ = 180°,可以推出 AB∥CD,理由是 .
A
B
C
D
1
2
3
4
5
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
叁
叁
肆
叁
叁
当堂达标
叁
(3) 从∠ =∠ 2 ,可以推出 AD∥BC,
理由是 .
(4) 从∠5 =∠ ,可以推出 AB∥CD,
理由是 .
3
内错角相等,两直线平行
ABC
同位角相等,两直线平行
A
B
C
D
1
2
3
4
5
叁
叁
肆
叁
叁
当堂达标
叁
理由如下:
∵ AC 平分∠DAB (已知),
∴∠1 =∠2 (角平分线的定义).
又∵∠1 =∠3 (已知),
∴∠2 =∠3 (等量代换).
∴ AB∥CD (内错角相等,两直线平行).
3. 如图,已知∠1 =∠3,AC 平分∠DAB,你能判定
哪两条直线平行?请说明理由.
2
3
A
B
C
D
)
)
1
(
解:AB∥CD.
叁
叁
肆
叁
叁
课堂小结
肆
课堂小结
肆
两条直线平行的判定方法
文字叙述 符号语言 图形
相等, 两直线平行 ∵ (已知), ∴ a∥b.
_______相等, 两直线平行 ∵ (已知), ∴ a∥b. ________互补, 两直线平行 ∵ (已知), ∴ a∥b. a
b
c
1
2
4
3
∠1 =∠2
∠3 =∠2
∠2 +∠4 = 180°
同位角
内错角
同旁内角
叁
叁
肆
叁
肆
课后作业
基础题:1.课后习题 第 1,2,3题。
提高题:2.请学有余力的同学完成课后习题第4题
谢
谢
第1课时 平行线的判定
第七章 命题与证明
2.平行线的证明
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
据说,人类知识的 75% 是在操作中学到的.
小明用下面的方法作出平行线,你认为他的作法对吗?为什么?
同旁内角互补,两直线平行.
同位角相等,两直线平行.
内错角相等,两直线平行.
叁
叁
肆
叁
壹
情境导入
同旁内角互补,两直线平行.
同位角相等,两直线平行.
内错角相等,两直线平行.
基本事实
证实其他命题的正确性
推理
原名、公理
一些条件
+
是否是真命题
叁
叁
肆
叁
壹
新知初探
贰
新知初探
探究一:平行线的判定
贰
基本事实 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
如图,∵∠3=∠2 (已知),
∴ a∥b (同位角相等,两直线平行).
应用格式:
a
b
c
3
2
新知初探
贰
试证明:
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
已知:如图,∠1 和∠2 是直线 a、b 被直线 c 截出的内错角,且∠1=∠2.
求证:a∥b.
a
b
3
2
1
c
新知初探
贰
解:∵∠1 = ∠2 (已知条件),
∠1 = ∠3(对顶角相等),
∴∠2 = ∠3(等量代换).
∴ a∥b (同位角相等,两直线平行).
已知:如图,∠1 和∠2 是直线 a、b 被直线 c 截出的内错角,且∠1=∠2.
求证:a∥b.
a
b
3
2
1
c
新知初探
贰
定理 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简述为:内错角相等,两直线平行.
∵∠1 =∠2(已知),
∴ a∥b (内错角相等,两直线平行).
应用格式:
知识要点
a
b
3
2
1
c
新知初探
贰
自主探究
试证明:
已知:如图,∠1 和∠2 是直线 a、b 被直线 c 截出的同旁内角,且∠1 与∠2 互补.
求证:a∥b.
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
a
b
3
2
1
c
新知初探
贰
证明:∵∠1 与∠2 互补 (已知),
∵∠3 +∠2 = 180° (补角的定义),
∴ ∠1=∠3 (等量代换).
∴ a∥b (同位角相等,两直线平行).
已知:如图,∠1 和∠2 是直线 a、b 被直线 c 截出的同旁内角,且∠1 与∠2 互补.
求证:a∥b.
a
b
3
2
1
c
∴ ∠1 +∠2 = 180° (互补的定义),
∴ ∠1 = 180°-∠2 (等式的性质).
∴∠3 = 180°-∠2 (等式的性质).
方法一
新知初探
贰
∵∠2+∠3=180°(补角的定义),
∴ ∠1=∠3(同角的补角相等).
∴ a∥b(内错角相等,两直线平行).
a
b
3
2
1
c
证明:∵∠1 与∠2 互补 (已知),
∴ ∠1 +∠2 = 180° (互补的定义),
已知:如图,∠1 和∠2 是直线 a、b 被直线 c 截出的同旁内角,且∠1 与∠2 互补.
求证:a∥b.
方法二
新知初探
贰
定理 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简述为:同旁内角互补,两直线平行.
∵∠1 +∠2 = 180°(已知),
∴ a∥b (同旁内角互补,两直线平行).
应用格式:
知识要点
a
b
3
2
1
c
新知初探
贰
① ∵∠1 =_____(已知),
∴ AB∥CE ( ).
② ∵∠1 +_____= 180°(已知),
∴ CD∥BF ( ).
③ ∵∠1 +∠5 = 180°(已知),
∴ _____∥_____ ( ).
CE
AB
∠2
④ ∵∠4 +_____= 180°(已知),
∴ AB∥CE ( ).
∠3
∠3
1
3
5
4
2
C
F
E
A
D
B
内错角相等,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
同旁内角互补,两直线平行
根据图形完成填空:
随堂练习
新知初探
探究二:平行线判定的应用
贰
(1)我们可以用如图的方法作出平行线,你能说说其中的道理吗
一、放
二、靠
三、推
四、画
内错角相等
两直线平行
(2)在一张不规则的四边形纸片上折出平行线,并予以证明,与同伴交流各自的折纸方法与证明过程
当堂达标
叁
当堂达标
叁
1. 对于图中标记的各角,下列条件能够推理得到 a∥b 的是 ( )
A.∠1 = ∠2 B.∠2 = ∠4
C.∠3 = ∠4 D.∠1 +∠4 = 180°
【解析】∠1 的对顶角与∠4 是同旁内角,若∠1 +∠4 = 180°,可以根据同旁内角互补,两直线平行得到 a∥b.
D
叁
叁
肆
叁
叁
当堂达标
叁
2. 如图.(1)从∠1 = ∠4,可以推出 ∥ ,
理由是 .
(2) 从∠ABC +∠ = 180°,可以推出 AB∥CD,理由是 .
A
B
C
D
1
2
3
4
5
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
叁
叁
肆
叁
叁
当堂达标
叁
(3) 从∠ =∠ 2 ,可以推出 AD∥BC,
理由是 .
(4) 从∠5 =∠ ,可以推出 AB∥CD,
理由是 .
3
内错角相等,两直线平行
ABC
同位角相等,两直线平行
A
B
C
D
1
2
3
4
5
叁
叁
肆
叁
叁
当堂达标
叁
理由如下:
∵ AC 平分∠DAB (已知),
∴∠1 =∠2 (角平分线的定义).
又∵∠1 =∠3 (已知),
∴∠2 =∠3 (等量代换).
∴ AB∥CD (内错角相等,两直线平行).
3. 如图,已知∠1 =∠3,AC 平分∠DAB,你能判定
哪两条直线平行?请说明理由.
2
3
A
B
C
D
)
)
1
(
解:AB∥CD.
叁
叁
肆
叁
叁
课堂小结
肆
课堂小结
肆
两条直线平行的判定方法
文字叙述 符号语言 图形
相等, 两直线平行 ∵ (已知), ∴ a∥b.
_______相等, 两直线平行 ∵ (已知), ∴ a∥b. ________互补, 两直线平行 ∵ (已知), ∴ a∥b. a
b
c
1
2
4
3
∠1 =∠2
∠3 =∠2
∠2 +∠4 = 180°
同位角
内错角
同旁内角
叁
叁
肆
叁
肆
课后作业
基础题:1.课后习题 第 1,2,3题。
提高题:2.请学有余力的同学完成课后习题第4题
谢
谢
同课章节目录
