7.2 第2课时 平行线的性质 课件(共27张PPT) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 7.2 第2课时 平行线的性质 课件(共27张PPT) 2025-2026学年数学北师大版(2024)八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 23:39:50 | ||
图片预览






文档简介
(共27张PPT)
第2课时 平行线的性质
第七章 命题与证明
2.平行线的证明
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
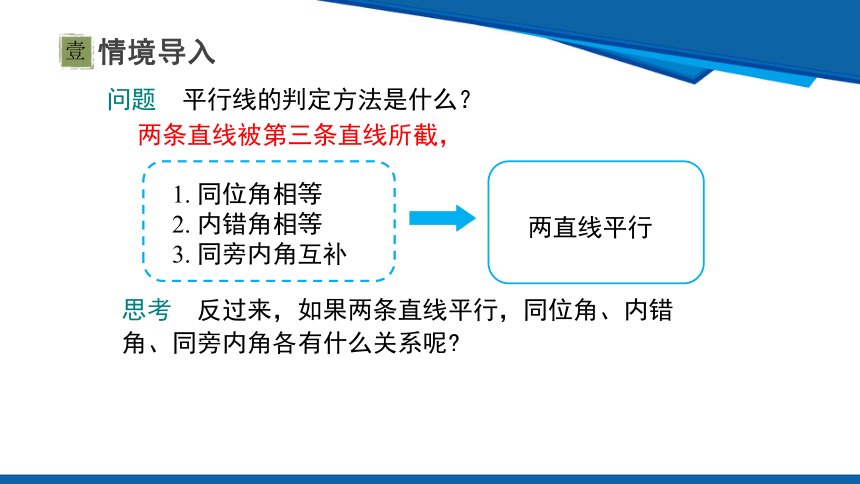
两直线平行
1. 同位角相等
2. 内错角相等
3. 同旁内角互补
问题 平行线的判定方法是什么?
思考 反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
两条直线被第三条直线所截,
叁
叁
肆
叁
壹
新知初探
贰
新知初探
探究一:平行线的性质
贰
问题1:根据“两条平行线被第三条直线所截,同位角相等”,你能作出相关的图形吗?
A
B
C
D
E
F
M
N
1
2
新知初探
贰
问题2:你能根据所作的图形写出已知、求证吗?
两条平行线被第三条直线所截,同位角相等.
文字语言
符号语言
A
B
C
D
E
F
M
N
1
2
已知:如图,直线 AB∥CD,∠1 和∠2 是直线 AB、CD 被直线 EF 所截得的同位角.
求证:∠1 =∠2.
新知初探
贰
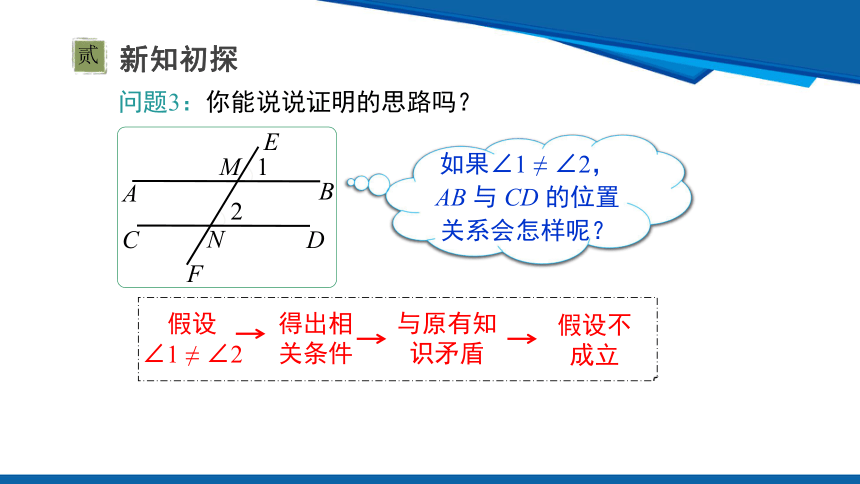
假设
∠1 ≠ ∠2
得出相关条件
与原有知识矛盾
假设不成立
问题3:你能说说证明的思路吗?
A
B
C
D
E
F
M
N
1
2
如果∠1 ≠ ∠2,AB 与 CD 的位置关系会怎样呢?
新知初探
贰
问题3:你能说说证明的思路吗?
G
H
这与基本事实“过直线外一点有且只有一条直线与这条直线平行”相矛盾.
这说明∠1 ≠ ∠2 的假设不成立,所以∠1 =∠2.
A
B
C
D
E
F
M
N
1
2
证明:假设∠1 ≠ ∠2,过点 M 作直线 GH,使∠EMH =∠2,如图.
根据“同位角相等,两直线平行”,可知 GH∥CD.
又因为 AB∥CD,这样经过点 M 存在两条直线 AB 和 GH 都与直线 CD 平行.
假设原命题不成立
进行推理,产生矛盾
假设不成立,原命题成立
新知初探
贰
归纳总结
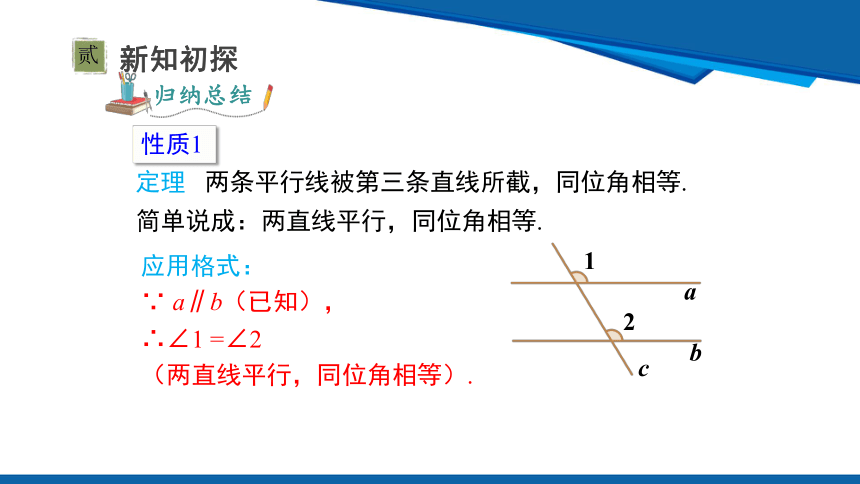
定理 两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
∴∠1 =∠2
(两直线平行,同位角相等).
∵ a∥b(已知),
应用格式:
a
b
c
1
2
性质1
新知初探
贰
议一议
利用上面的定理,我们可以证明:
两直线平行,内错角相等.
两直线平行,同旁内角互补.
尝试来证明一下!
新知初探
贰
证一证
已知:如图,直线 l1∥l2,∠1 和∠2 是直线 l1,l2 被直线 l 截得的内错角.
求证:∠1 =∠2.
证明:∵ l1∥l2 (已知),
∴∠1=∠3 (两条直线平行,同位角相等).
∵∠2=∠3 (对顶角相等),
∴∠1=∠2 (等量代换).
l1
l2
3
2
1
l
新知初探
贰
知识要点
定理 两条平行直线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
∵ l1∥l2(已知),
∴ ∠1 =∠2(两直线平行,内错角相等).
应用格式:
l1
l2
3
2
1
l
性质2
新知初探
贰
已知:如图,直线 l1∥l2,∠1 和∠2 是直线 l1,l2 被直线 l 截得的同旁内角.
求证:∠1 +∠2 = 180°.
证明:∵ l1∥l2 (已知),
∴∠2 =∠3 (两条直线平行,同位角相等).
∵∠1 +∠3 = 180° (平角的定义),
∴∠1 +∠2 = 180° (等量代换) .
证一证
l1
l2
3
2
1
l
新知初探
贰
知识要点
定理 两条平行直线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
∵ l1∥l2(已知),
∴ ∠1 +∠2 = 180°
(两直线平行,同旁内角互补).
应用格式:
l1
l2
3
2
1
l
性质3
新知初探
探究二:典例精析
贰
例 已知:如图,b∥a,c∥a,∠1,∠2,∠3 是直线 a,b,c 被直线 d 截出的同位角.
求证:b∥c.
证明:∵b∥a(已知),
∴∠2 =∠1(两直线平行,同位角相等).
∵c∥a(已知),
∴∠3 =∠1(两直线平行,同位角相等).
∴∠2 =∠3(等量代换).
∴b∥c(同位角相等,两直线平行).
b
c
3
2
1
a
d
新知初探
贰
知识要点
符号语言:
如图,b∥a,c∥a(已知),
∴ b∥c
(平行于同一条直线的两条直线平行).
定理 平行于同一条直线的两条直线平行.
b
c
3
2
1
a
新知初探
贰
证明一个命题的一般步骤:
(1) 弄清题设和结论;
(2) 根据题意画出相应的图形;
(3) 根据题设和结论写出已知,求证;
(4) 分析证明思路,写出证明过程.
归纳总结
新知初探
贰
角的数量关系
线的位置关系
判定
性质
同位角相等
内错角相等
同旁内角互补
两直线平行
条件
结论
结论
条件
判定
性质
平行线的判定定理与性质定理互为逆命题
讨论:平行线三个性质的条件是什么?结论是什么?它与判定有什么区别?(分组讨论)
当堂达标
叁
当堂达标
叁
解:∵ AB∥DE ( ),
∴∠A =_______ ( ).
∵ AC∥DF ( ) ,
∴∠D =______ ( ).
∴∠A =∠D ( ).
1. 如图 1,若 AB∥DE,AC∥DF,试说明∠A =∠D. 请补全下面的解答过程,括号内填写依据.
P
F
C
E
B
A
D
图 1
已知
∠CPE
两直线平行,同位角相等
已知
∠CPE
两直线平行,同位角相等
等量代换
叁
叁
肆
叁
叁
当堂达标
叁
解:∵ AB∥DE ( ),
∴∠A = ______ ( ).
∵AC∥DF ( ) ,
∴∠D + _______=180° ( ).
∴∠A +∠D=180° ( ).
2. 如图 2,若 AB∥DE,AC∥DF,试说明∠A +∠D = 180°. 请补全下面的解答过程,括号内填写依据.
图2
F
C
E
B
A
D
P
已知
∠CPD
两直线平行,同位角相等
已知
∠CPD
两直线平行,同旁内角互补
等量代换
叁
叁
肆
叁
叁
当堂达标
叁
3. 如图,在△ABC 中,CE⊥AB 于点 E,DF⊥AB 于点 F,AC∥ED,CE 是∠ACB 的平分线,则∠EDF =∠BDF,请说明理由.
解:∵ CE⊥AB,DF⊥AB(已知),
∴ DF∥EC(同位角相等,两直线平行).
∴ ∠DFB = ∠CEB = 90°(垂直的定义),
叁
叁
肆
叁
叁
当堂达标
叁
∴∠BDF =∠1(两直线平行,同位角相等),
∠EDF =∠3(两直线平行,内错角相等).
∵ AC∥ED(已知),
∴ ∠3 =∠2(两直线平行,内错角相等).
∴ ∠EDF =∠2(等量代换).
又∵ CE 平分∠ACB(已知),
∴ ∠1 =∠2(角平分线定义).
∴ ∠EDF =∠BDF(等量代换).
叁
叁
肆
叁
叁
课堂小结
肆
课堂小结
肆
平行线的性质
性质定理
命题证明步骤
两直线平行,同位角相等
根据题意画出图形
根据题意写出已知及求证
写出证明过程
两直线平行,内错角相等
两直线平行,同旁内角互补
平行于同一条直线的两条直线平行
叁
叁
肆
叁
肆
课后作业
基础题:1.课后习题 第 5,6题。
提高题:2.请学有余力的同学完成课后习题第7,8题
谢
谢
第2课时 平行线的性质
第七章 命题与证明
2.平行线的证明
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
两直线平行
1. 同位角相等
2. 内错角相等
3. 同旁内角互补
问题 平行线的判定方法是什么?
思考 反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
两条直线被第三条直线所截,
叁
叁
肆
叁
壹
新知初探
贰
新知初探
探究一:平行线的性质
贰
问题1:根据“两条平行线被第三条直线所截,同位角相等”,你能作出相关的图形吗?
A
B
C
D
E
F
M
N
1
2
新知初探
贰
问题2:你能根据所作的图形写出已知、求证吗?
两条平行线被第三条直线所截,同位角相等.
文字语言
符号语言
A
B
C
D
E
F
M
N
1
2
已知:如图,直线 AB∥CD,∠1 和∠2 是直线 AB、CD 被直线 EF 所截得的同位角.
求证:∠1 =∠2.
新知初探
贰
假设
∠1 ≠ ∠2
得出相关条件
与原有知识矛盾
假设不成立
问题3:你能说说证明的思路吗?
A
B
C
D
E
F
M
N
1
2
如果∠1 ≠ ∠2,AB 与 CD 的位置关系会怎样呢?
新知初探
贰
问题3:你能说说证明的思路吗?
G
H
这与基本事实“过直线外一点有且只有一条直线与这条直线平行”相矛盾.
这说明∠1 ≠ ∠2 的假设不成立,所以∠1 =∠2.
A
B
C
D
E
F
M
N
1
2
证明:假设∠1 ≠ ∠2,过点 M 作直线 GH,使∠EMH =∠2,如图.
根据“同位角相等,两直线平行”,可知 GH∥CD.
又因为 AB∥CD,这样经过点 M 存在两条直线 AB 和 GH 都与直线 CD 平行.
假设原命题不成立
进行推理,产生矛盾
假设不成立,原命题成立
新知初探
贰
归纳总结
定理 两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
∴∠1 =∠2
(两直线平行,同位角相等).
∵ a∥b(已知),
应用格式:
a
b
c
1
2
性质1
新知初探
贰
议一议
利用上面的定理,我们可以证明:
两直线平行,内错角相等.
两直线平行,同旁内角互补.
尝试来证明一下!
新知初探
贰
证一证
已知:如图,直线 l1∥l2,∠1 和∠2 是直线 l1,l2 被直线 l 截得的内错角.
求证:∠1 =∠2.
证明:∵ l1∥l2 (已知),
∴∠1=∠3 (两条直线平行,同位角相等).
∵∠2=∠3 (对顶角相等),
∴∠1=∠2 (等量代换).
l1
l2
3
2
1
l
新知初探
贰
知识要点
定理 两条平行直线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
∵ l1∥l2(已知),
∴ ∠1 =∠2(两直线平行,内错角相等).
应用格式:
l1
l2
3
2
1
l
性质2
新知初探
贰
已知:如图,直线 l1∥l2,∠1 和∠2 是直线 l1,l2 被直线 l 截得的同旁内角.
求证:∠1 +∠2 = 180°.
证明:∵ l1∥l2 (已知),
∴∠2 =∠3 (两条直线平行,同位角相等).
∵∠1 +∠3 = 180° (平角的定义),
∴∠1 +∠2 = 180° (等量代换) .
证一证
l1
l2
3
2
1
l
新知初探
贰
知识要点
定理 两条平行直线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
∵ l1∥l2(已知),
∴ ∠1 +∠2 = 180°
(两直线平行,同旁内角互补).
应用格式:
l1
l2
3
2
1
l
性质3
新知初探
探究二:典例精析
贰
例 已知:如图,b∥a,c∥a,∠1,∠2,∠3 是直线 a,b,c 被直线 d 截出的同位角.
求证:b∥c.
证明:∵b∥a(已知),
∴∠2 =∠1(两直线平行,同位角相等).
∵c∥a(已知),
∴∠3 =∠1(两直线平行,同位角相等).
∴∠2 =∠3(等量代换).
∴b∥c(同位角相等,两直线平行).
b
c
3
2
1
a
d
新知初探
贰
知识要点
符号语言:
如图,b∥a,c∥a(已知),
∴ b∥c
(平行于同一条直线的两条直线平行).
定理 平行于同一条直线的两条直线平行.
b
c
3
2
1
a
新知初探
贰
证明一个命题的一般步骤:
(1) 弄清题设和结论;
(2) 根据题意画出相应的图形;
(3) 根据题设和结论写出已知,求证;
(4) 分析证明思路,写出证明过程.
归纳总结
新知初探
贰
角的数量关系
线的位置关系
判定
性质
同位角相等
内错角相等
同旁内角互补
两直线平行
条件
结论
结论
条件
判定
性质
平行线的判定定理与性质定理互为逆命题
讨论:平行线三个性质的条件是什么?结论是什么?它与判定有什么区别?(分组讨论)
当堂达标
叁
当堂达标
叁
解:∵ AB∥DE ( ),
∴∠A =_______ ( ).
∵ AC∥DF ( ) ,
∴∠D =______ ( ).
∴∠A =∠D ( ).
1. 如图 1,若 AB∥DE,AC∥DF,试说明∠A =∠D. 请补全下面的解答过程,括号内填写依据.
P
F
C
E
B
A
D
图 1
已知
∠CPE
两直线平行,同位角相等
已知
∠CPE
两直线平行,同位角相等
等量代换
叁
叁
肆
叁
叁
当堂达标
叁
解:∵ AB∥DE ( ),
∴∠A = ______ ( ).
∵AC∥DF ( ) ,
∴∠D + _______=180° ( ).
∴∠A +∠D=180° ( ).
2. 如图 2,若 AB∥DE,AC∥DF,试说明∠A +∠D = 180°. 请补全下面的解答过程,括号内填写依据.
图2
F
C
E
B
A
D
P
已知
∠CPD
两直线平行,同位角相等
已知
∠CPD
两直线平行,同旁内角互补
等量代换
叁
叁
肆
叁
叁
当堂达标
叁
3. 如图,在△ABC 中,CE⊥AB 于点 E,DF⊥AB 于点 F,AC∥ED,CE 是∠ACB 的平分线,则∠EDF =∠BDF,请说明理由.
解:∵ CE⊥AB,DF⊥AB(已知),
∴ DF∥EC(同位角相等,两直线平行).
∴ ∠DFB = ∠CEB = 90°(垂直的定义),
叁
叁
肆
叁
叁
当堂达标
叁
∴∠BDF =∠1(两直线平行,同位角相等),
∠EDF =∠3(两直线平行,内错角相等).
∵ AC∥ED(已知),
∴ ∠3 =∠2(两直线平行,内错角相等).
∴ ∠EDF =∠2(等量代换).
又∵ CE 平分∠ACB(已知),
∴ ∠1 =∠2(角平分线定义).
∴ ∠EDF =∠BDF(等量代换).
叁
叁
肆
叁
叁
课堂小结
肆
课堂小结
肆
平行线的性质
性质定理
命题证明步骤
两直线平行,同位角相等
根据题意画出图形
根据题意写出已知及求证
写出证明过程
两直线平行,内错角相等
两直线平行,同旁内角互补
平行于同一条直线的两条直线平行
叁
叁
肆
叁
肆
课后作业
基础题:1.课后习题 第 5,6题。
提高题:2.请学有余力的同学完成课后习题第7,8题
谢
谢
同课章节目录
