5.7三角函数的应用 同步练习(含答案)
文档属性
| 名称 | 5.7三角函数的应用 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 440.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 17:41:32 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
5.7三角函数的应用
一、单选题
1.若函数的图像关于直线对称,那么a=( )
A. B.- C.1 D.-1
2.已知两座灯塔A和B与海洋观察站C的距离都等于a km,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与B的距离为( )
A.akm B. akm C. akm D.2akm
3.(2021高一下·聊城期末)泰山于1987年12月12日被列为世界文化与自然双重遗产,泰山及其周边坐落着许多古塔.某兴趣小组为了测量某古塔的高度,如图所示,在地面上一点 处测得塔顶 的仰角为 ,在塔底 处测得 处的俯角为 .已知山岭高 为256米,则塔高 为( )
A. 米 B. 米
C. 米 D. 米
4.(2022·吉林模拟)智能主动降噪耳机工作的原理是通过耳机两端的噪声采集器采集周围的噪声,然后通过主动降噪芯片生成的声波来抵消噪声(如图).已知噪声的声波曲线是,通过主动降噪芯片生成的声波曲线是(其中),则( )
A. B.π C. D.
5.(2022·通州模拟)太阳高度角是太阳光线与地面所成的角(即太阳在当地的仰角).设地球表面某地正午太阳高度角为,为此时太阳直射点纬度,为当地纬度值,那么这三个量满足.通州区某校学生科技社团尝试估测通州区当地纬度值(取正值),选择春分当日()测算正午太阳高度角.他们将长度为1米的木杆垂直立于地面,测量木杆的影长.分为甲、乙、丙、丁四个小组在同一场地进行,测量结果如下:
组别 甲组 乙组 丙组 丁组
木杆影长度(米) 0.82 0.80 0.83 0.85
则四组中对通州区当地纬度估测值最大的一组是( )
A.甲组 B.乙组 C.丙组 D.丁组
6.(2022·红河模拟)红河州个旧市是一个风景优美的宜居城市,如图是个旧宝华公园的摩天轮,半径为20米,圆心O距地面的高度为25米,摩天轮运行时按逆时针匀速旋转,转一周需要10分钟.摩天轮上的点P的起始位置在最低点处.若游客在距离地面至少35米的高度能够将个旧市区美景尽收眼底,则摩天轮转动一周内具有最佳视觉效果的时间长度(单位:分钟)为( )
A. B.3 C. D.
7.(2021高一下·阎良期末)已知函数,若存在实数、,使得,且,则的最大值为( )
A.9 B.8 C.7 D.5
二、多选题
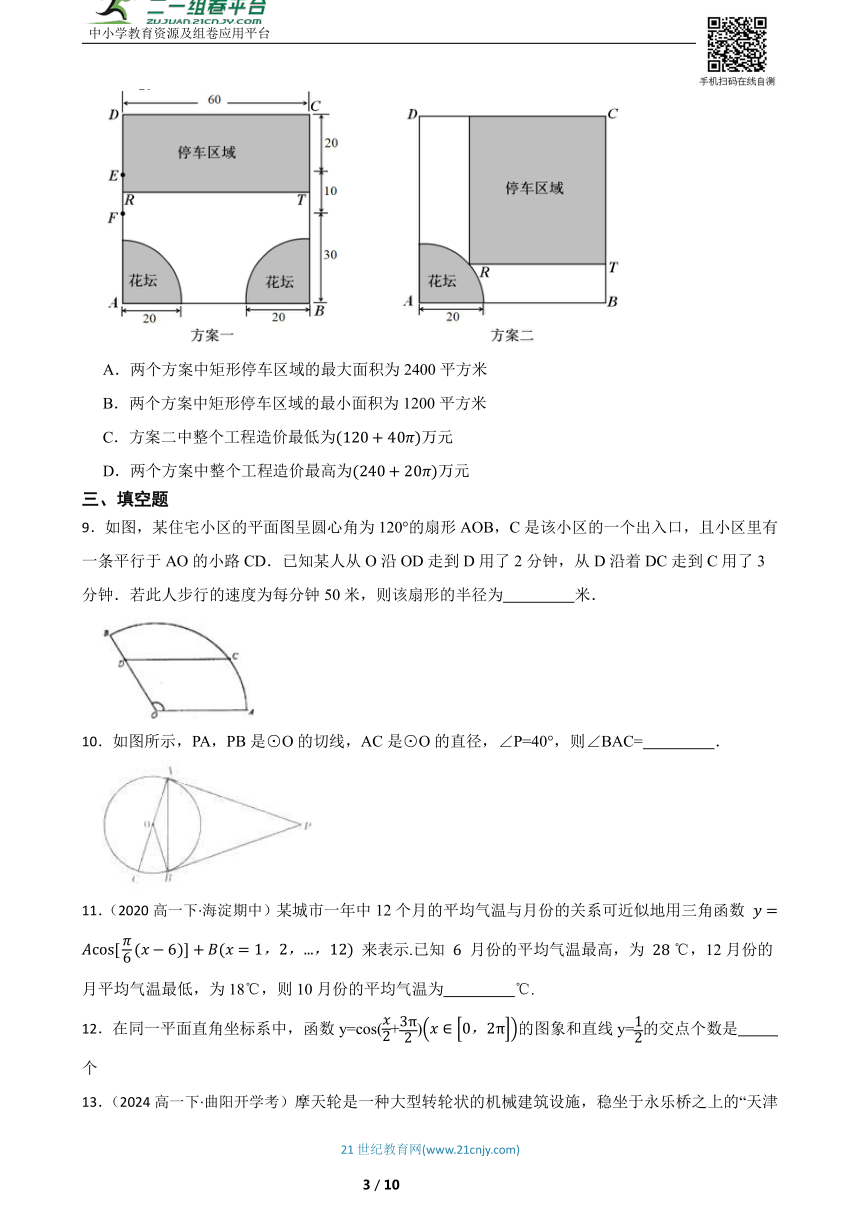
8.(2022高一下·湖北期中)某商场前有一块边长为60米的正方形地皮,为了方便消费者停车,拟划出一块矩形区域用于停放电动车等,同时为了美观,建造扇形花坛,现设计两种方案如图所示,方案一:,在线段上且,方案二:在圆弧上且.若花坛区域工程造价0.2万元/平方米,停车区域工程造价为0.1万元/平方米,则下列说法正确的是( )
A.两个方案中矩形停车区域的最大面积为2400平方米
B.两个方案中矩形停车区域的最小面积为1200平方米
C.方案二中整个工程造价最低为万元
D.两个方案中整个工程造价最高为万元
三、填空题
9.如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,C是该小区的一个出入口,且小区里有一条平行于AO的小路CD.已知某人从O沿OD走到D用了2分钟,从D沿着DC走到C用了3分钟.若此人步行的速度为每分钟50米,则该扇形的半径为 米.
10.如图所示,PA,PB是⊙O的切线,AC是⊙O的直径,∠P=40°,则∠BAC= .
11.(2020高一下·海淀期中)某城市一年中12个月的平均气温与月份的关系可近似地用三角函数 来表示.已知 月份的平均气温最高,为 ℃,12月份的月平均气温最低,为18℃,则10月份的平均气温为 ℃.
12.在同一平面直角坐标系中,函数y=cos(+)的图象和直线y=的交点个数是 个
13.(2024高一下·曲阳开学考)摩天轮是一种大型转轮状的机械建筑设施,稳坐于永乐桥之上的“天津之眼”作为世界上唯一一座建在桥上的摩天轮,其巧夺天工和奇思妙想确是当之无愧的“世界第一”.如图,永乐桥摩天轮的直径为 ,到达最高点时,距离地面的高度为 ,能看到方圆 以内的景致,是名副其实的“天津之眼”.实际上,单从高度角度来看,天津之眼超越了曾大名鼎鼎的伦敦之眼而跃居世界第一.永乐桥摩天轮设置有48个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周大约需要 .游客甲坐上摩天轮的座舱,开始转到 后距离地面的高度为 ,则转到 后距离地面的高度为 ,在转动一周的过程中, 关于 的函数解析式为 .
14.(2019高三上·吴中月考)已知直线 与函数 的图像恰有四个公共点 , , , ,其中 ,则 .
四、解答题
15.(2019高一上·江苏月考)如图为某儿童游乐场一个小型摩天轮示意图,该摩天轮近似看作半径为 的圆,圆上最低点A与地面距离为 ,摩天轮每60秒匀速转动一圈,摩天轮上某点B的起始位置在最低点A处.图中 与地面垂直,以 为始边,逆时针转动 角到 ,设B点与地面间的距离为 .
(1)求h与 间关系的函数解析式;
(2)设从 开始转动,经过t秒后到达 ,求h与t之间的函数关系式;
(3)如果离地面高度不低于 才能获得最佳观景效果,在摩天轮转动的一圈内,有多长时间B点在最佳观景效果高度?
16.(2018高一下·西华期末)如图,一个水轮的半径为 ,水轮圆心 距离水面 ,已知水轮每分钟转动 圈,如果当水轮上点 从水中浮现时(图中点 )开始计算时间。
(1)将点 距离水面的高度 表示为时间 的函数;
(2)点 第一次到达最高点大约需要多少时间?
17.(2020高一上·苏州期末)摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢的往上转,可以从高处俯瞰四周的景色(如图1).某摩天轮的最高点距离地面的高度为 90 米,最低点距离地面 10 米,摩天轮上均匀设置了 36 个座舱(如图2).开启后摩天轮按逆时针方向匀速转动,游客在座舱离地面最近时的位置进入座舱,摩天轮转完一周后在相同的位置离开座舱.摩天轮转一周需要30分钟,当游客甲坐上摩天轮的座舱开始计时.
(1)经过t 分钟后游客甲距离地面的高度为H 米,已知H 关于t 的函数关系式满足H(t)=Asin(ωt+φ)+B其中A>0,ω> 0),求摩天轮转动一周的解析式 H(t);
(2)问:游客甲坐上摩天轮后多长时间,距离地面的高度恰好为 30 米?
(3)若游客乙在游客甲之后进入座舱,且中间相隔 5 个座舱,在摩天轮转动一周的过程中,记两人距离地面的高度差为 h 米,求 h 的最大值.
18.(2018高一下·威远期中)如图,在半径为 ,圆心角为 的扇形弧 上任取一点 ,作扇形的内接矩形 ,使 点在 上,点 都在 上,求这个矩形面积的最大值及相应的 的值.
19.(2017高一下·上饶期中)已知函数f(x)=sin(ωx+φ)(ω>0,0≤φ≤π)是R上的偶函数,其图象关于点 对称,且在区间 上是单调函数,求φ和ω的值.
答案解析部分
1.【答案】D
【知识点】三角函数模型的简单应用
2.【答案】B
【知识点】三角函数模型的简单应用
3.【答案】B
【知识点】三角函数模型的简单应用
4.【答案】C
【知识点】三角函数模型的简单应用
5.【答案】D
【知识点】三角函数模型的简单应用
6.【答案】C
【知识点】三角函数模型的简单应用
7.【答案】A
【知识点】三角函数模型的简单应用
8.【答案】A,B
【知识点】三角函数模型的简单应用;函数的应用
9.【答案】50
【知识点】三角函数模型的简单应用
10.【答案】20°
【知识点】三角函数模型的简单应用
11.【答案】20.5
【知识点】三角函数模型的简单应用
12.【答案】2
【知识点】三角函数模型的简单应用
13.【答案】; ,
【知识点】函数解析式的求解及常用方法;三角函数模型的简单应用
14.【答案】-2
【知识点】三角函数模型的简单应用
15.【答案】(1)解:以圆心O为原点,建立如图所示的平面直角坐标系,
则以 为始边, 为终边的角为 ,
故点B的坐标为 ,
.
(2)解:点A在圆上转动的角速度是 ,故t秒转过的弧度数为 ,
, .
(3)解:由
得 ,
,
故转动一圈最佳观景效果持续的时间为20秒
答:一个周期内B点在最佳观赏效果高度持续的时间为20秒.
【知识点】三角函数模型的简单应用
16.【答案】(1)解:依题意可知 的最大值为 ,最小为 ,
∴ ;
∵ 每秒钟内所转过的角为 ,得 ,
当 时, ,得 ,即 ,故所求的函数关系式为
(2)解:令 ,得 ,
取 ,得 ,
故点 第一次到达最高点大约需要
【知识点】三角函数模型的简单应用
17.【答案】(1)解:由题意可设 ,摩天轮的最高点距离地面的高度为90米,最低点距离地面10米,
,得 .
又函数周期为30, ,
( ),
又 时, ,所以 ,即 , 可取 ,
所以
(2)解: , 解得 ,
所以游客甲坐上摩天轮5分钟后,距离地面的高度恰好为30米
(3)解:由题意知相邻两个座舱到达最低点的时间间隔为 ,游客甲,乙中间相隔5个座舱,
则游客乙在游客甲之后5分钟进入座舱,若甲在摩天轮上坐了 ( )分钟,则游客乙在摩天轮上坐了 分钟,所以高度差为:
当 即 时,h取得最大值 .
【知识点】三角函数模型的简单应用
18.【答案】解:连接 ,则 ,设 ,
在 中, ,
四边形 是矩形, ,
,在 中,
于是,
当 时, ,
当 时, ,
的最大值是 ,相应的
【知识点】正弦函数的性质;三角函数模型的简单应用
19.【答案】解:由f(x)是偶函数,得f(﹣x)=f(x),
即sin(﹣ωx+φ)=sin(ωx+φ),
所以﹣cosφsinωx=cosφsinωx,
对任意x都成立,且w>0,
所以得cosφ=0.
依题设0≤φ≤π,所以解得φ= ,
由f(x)的图象关于点M对称,
得 ,
取x=0,得f( )=sin( )=cos ,
∴f( )=sin( )=cos ,
∴cos =0,
又w>0,得 = +kπ,k=0,1,2,3,…
∴ω= (2k+1),k=0,1,2,…
当k=0时,ω= ,f(x)=sin( )在[0, ]上是减函数,满足题意;
当k=1时,ω=2,f(x)=sin(2x+ )=cos2x,在[0, ]上是减函数,满足题意;
当k=2时,ω= ,f(x)=sin( x+ )在[0, ]上不是单调函数;
所以,综合得ω= 或2
【知识点】三角函数模型的简单应用
21世纪教育网(www.21cnjy.com)
2 / 11
5.7三角函数的应用
一、单选题
1.若函数的图像关于直线对称,那么a=( )
A. B.- C.1 D.-1
2.已知两座灯塔A和B与海洋观察站C的距离都等于a km,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与B的距离为( )
A.akm B. akm C. akm D.2akm
3.(2021高一下·聊城期末)泰山于1987年12月12日被列为世界文化与自然双重遗产,泰山及其周边坐落着许多古塔.某兴趣小组为了测量某古塔的高度,如图所示,在地面上一点 处测得塔顶 的仰角为 ,在塔底 处测得 处的俯角为 .已知山岭高 为256米,则塔高 为( )
A. 米 B. 米
C. 米 D. 米
4.(2022·吉林模拟)智能主动降噪耳机工作的原理是通过耳机两端的噪声采集器采集周围的噪声,然后通过主动降噪芯片生成的声波来抵消噪声(如图).已知噪声的声波曲线是,通过主动降噪芯片生成的声波曲线是(其中),则( )
A. B.π C. D.
5.(2022·通州模拟)太阳高度角是太阳光线与地面所成的角(即太阳在当地的仰角).设地球表面某地正午太阳高度角为,为此时太阳直射点纬度,为当地纬度值,那么这三个量满足.通州区某校学生科技社团尝试估测通州区当地纬度值(取正值),选择春分当日()测算正午太阳高度角.他们将长度为1米的木杆垂直立于地面,测量木杆的影长.分为甲、乙、丙、丁四个小组在同一场地进行,测量结果如下:
组别 甲组 乙组 丙组 丁组
木杆影长度(米) 0.82 0.80 0.83 0.85
则四组中对通州区当地纬度估测值最大的一组是( )
A.甲组 B.乙组 C.丙组 D.丁组
6.(2022·红河模拟)红河州个旧市是一个风景优美的宜居城市,如图是个旧宝华公园的摩天轮,半径为20米,圆心O距地面的高度为25米,摩天轮运行时按逆时针匀速旋转,转一周需要10分钟.摩天轮上的点P的起始位置在最低点处.若游客在距离地面至少35米的高度能够将个旧市区美景尽收眼底,则摩天轮转动一周内具有最佳视觉效果的时间长度(单位:分钟)为( )
A. B.3 C. D.
7.(2021高一下·阎良期末)已知函数,若存在实数、,使得,且,则的最大值为( )
A.9 B.8 C.7 D.5
二、多选题
8.(2022高一下·湖北期中)某商场前有一块边长为60米的正方形地皮,为了方便消费者停车,拟划出一块矩形区域用于停放电动车等,同时为了美观,建造扇形花坛,现设计两种方案如图所示,方案一:,在线段上且,方案二:在圆弧上且.若花坛区域工程造价0.2万元/平方米,停车区域工程造价为0.1万元/平方米,则下列说法正确的是( )
A.两个方案中矩形停车区域的最大面积为2400平方米
B.两个方案中矩形停车区域的最小面积为1200平方米
C.方案二中整个工程造价最低为万元
D.两个方案中整个工程造价最高为万元
三、填空题
9.如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,C是该小区的一个出入口,且小区里有一条平行于AO的小路CD.已知某人从O沿OD走到D用了2分钟,从D沿着DC走到C用了3分钟.若此人步行的速度为每分钟50米,则该扇形的半径为 米.
10.如图所示,PA,PB是⊙O的切线,AC是⊙O的直径,∠P=40°,则∠BAC= .
11.(2020高一下·海淀期中)某城市一年中12个月的平均气温与月份的关系可近似地用三角函数 来表示.已知 月份的平均气温最高,为 ℃,12月份的月平均气温最低,为18℃,则10月份的平均气温为 ℃.
12.在同一平面直角坐标系中,函数y=cos(+)的图象和直线y=的交点个数是 个
13.(2024高一下·曲阳开学考)摩天轮是一种大型转轮状的机械建筑设施,稳坐于永乐桥之上的“天津之眼”作为世界上唯一一座建在桥上的摩天轮,其巧夺天工和奇思妙想确是当之无愧的“世界第一”.如图,永乐桥摩天轮的直径为 ,到达最高点时,距离地面的高度为 ,能看到方圆 以内的景致,是名副其实的“天津之眼”.实际上,单从高度角度来看,天津之眼超越了曾大名鼎鼎的伦敦之眼而跃居世界第一.永乐桥摩天轮设置有48个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周大约需要 .游客甲坐上摩天轮的座舱,开始转到 后距离地面的高度为 ,则转到 后距离地面的高度为 ,在转动一周的过程中, 关于 的函数解析式为 .
14.(2019高三上·吴中月考)已知直线 与函数 的图像恰有四个公共点 , , , ,其中 ,则 .
四、解答题
15.(2019高一上·江苏月考)如图为某儿童游乐场一个小型摩天轮示意图,该摩天轮近似看作半径为 的圆,圆上最低点A与地面距离为 ,摩天轮每60秒匀速转动一圈,摩天轮上某点B的起始位置在最低点A处.图中 与地面垂直,以 为始边,逆时针转动 角到 ,设B点与地面间的距离为 .
(1)求h与 间关系的函数解析式;
(2)设从 开始转动,经过t秒后到达 ,求h与t之间的函数关系式;
(3)如果离地面高度不低于 才能获得最佳观景效果,在摩天轮转动的一圈内,有多长时间B点在最佳观景效果高度?
16.(2018高一下·西华期末)如图,一个水轮的半径为 ,水轮圆心 距离水面 ,已知水轮每分钟转动 圈,如果当水轮上点 从水中浮现时(图中点 )开始计算时间。
(1)将点 距离水面的高度 表示为时间 的函数;
(2)点 第一次到达最高点大约需要多少时间?
17.(2020高一上·苏州期末)摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢的往上转,可以从高处俯瞰四周的景色(如图1).某摩天轮的最高点距离地面的高度为 90 米,最低点距离地面 10 米,摩天轮上均匀设置了 36 个座舱(如图2).开启后摩天轮按逆时针方向匀速转动,游客在座舱离地面最近时的位置进入座舱,摩天轮转完一周后在相同的位置离开座舱.摩天轮转一周需要30分钟,当游客甲坐上摩天轮的座舱开始计时.
(1)经过t 分钟后游客甲距离地面的高度为H 米,已知H 关于t 的函数关系式满足H(t)=Asin(ωt+φ)+B其中A>0,ω> 0),求摩天轮转动一周的解析式 H(t);
(2)问:游客甲坐上摩天轮后多长时间,距离地面的高度恰好为 30 米?
(3)若游客乙在游客甲之后进入座舱,且中间相隔 5 个座舱,在摩天轮转动一周的过程中,记两人距离地面的高度差为 h 米,求 h 的最大值.
18.(2018高一下·威远期中)如图,在半径为 ,圆心角为 的扇形弧 上任取一点 ,作扇形的内接矩形 ,使 点在 上,点 都在 上,求这个矩形面积的最大值及相应的 的值.
19.(2017高一下·上饶期中)已知函数f(x)=sin(ωx+φ)(ω>0,0≤φ≤π)是R上的偶函数,其图象关于点 对称,且在区间 上是单调函数,求φ和ω的值.
答案解析部分
1.【答案】D
【知识点】三角函数模型的简单应用
2.【答案】B
【知识点】三角函数模型的简单应用
3.【答案】B
【知识点】三角函数模型的简单应用
4.【答案】C
【知识点】三角函数模型的简单应用
5.【答案】D
【知识点】三角函数模型的简单应用
6.【答案】C
【知识点】三角函数模型的简单应用
7.【答案】A
【知识点】三角函数模型的简单应用
8.【答案】A,B
【知识点】三角函数模型的简单应用;函数的应用
9.【答案】50
【知识点】三角函数模型的简单应用
10.【答案】20°
【知识点】三角函数模型的简单应用
11.【答案】20.5
【知识点】三角函数模型的简单应用
12.【答案】2
【知识点】三角函数模型的简单应用
13.【答案】; ,
【知识点】函数解析式的求解及常用方法;三角函数模型的简单应用
14.【答案】-2
【知识点】三角函数模型的简单应用
15.【答案】(1)解:以圆心O为原点,建立如图所示的平面直角坐标系,
则以 为始边, 为终边的角为 ,
故点B的坐标为 ,
.
(2)解:点A在圆上转动的角速度是 ,故t秒转过的弧度数为 ,
, .
(3)解:由
得 ,
,
故转动一圈最佳观景效果持续的时间为20秒
答:一个周期内B点在最佳观赏效果高度持续的时间为20秒.
【知识点】三角函数模型的简单应用
16.【答案】(1)解:依题意可知 的最大值为 ,最小为 ,
∴ ;
∵ 每秒钟内所转过的角为 ,得 ,
当 时, ,得 ,即 ,故所求的函数关系式为
(2)解:令 ,得 ,
取 ,得 ,
故点 第一次到达最高点大约需要
【知识点】三角函数模型的简单应用
17.【答案】(1)解:由题意可设 ,摩天轮的最高点距离地面的高度为90米,最低点距离地面10米,
,得 .
又函数周期为30, ,
( ),
又 时, ,所以 ,即 , 可取 ,
所以
(2)解: , 解得 ,
所以游客甲坐上摩天轮5分钟后,距离地面的高度恰好为30米
(3)解:由题意知相邻两个座舱到达最低点的时间间隔为 ,游客甲,乙中间相隔5个座舱,
则游客乙在游客甲之后5分钟进入座舱,若甲在摩天轮上坐了 ( )分钟,则游客乙在摩天轮上坐了 分钟,所以高度差为:
当 即 时,h取得最大值 .
【知识点】三角函数模型的简单应用
18.【答案】解:连接 ,则 ,设 ,
在 中, ,
四边形 是矩形, ,
,在 中,
于是,
当 时, ,
当 时, ,
的最大值是 ,相应的
【知识点】正弦函数的性质;三角函数模型的简单应用
19.【答案】解:由f(x)是偶函数,得f(﹣x)=f(x),
即sin(﹣ωx+φ)=sin(ωx+φ),
所以﹣cosφsinωx=cosφsinωx,
对任意x都成立,且w>0,
所以得cosφ=0.
依题设0≤φ≤π,所以解得φ= ,
由f(x)的图象关于点M对称,
得 ,
取x=0,得f( )=sin( )=cos ,
∴f( )=sin( )=cos ,
∴cos =0,
又w>0,得 = +kπ,k=0,1,2,3,…
∴ω= (2k+1),k=0,1,2,…
当k=0时,ω= ,f(x)=sin( )在[0, ]上是减函数,满足题意;
当k=1时,ω=2,f(x)=sin(2x+ )=cos2x,在[0, ]上是减函数,满足题意;
当k=2时,ω= ,f(x)=sin( x+ )在[0, ]上不是单调函数;
所以,综合得ω= 或2
【知识点】三角函数模型的简单应用
21世纪教育网(www.21cnjy.com)
2 / 11
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
