3.1 第1课时 代数式 课件(共34张PPT)
文档属性
| 名称 | 3.1 第1课时 代数式 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 20:37:32 | ||
图片预览







文档简介
(共34张PPT)
北师大版数学七年级上册
第三章 整式及其加减
汇报人:孙老师
汇报班级:X级X班
3.1 代数式
3.1 第1课时 代数式
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.能用字母表示运算律以及计算公式.
2. 能用字母表示一些简单问题中的数量关系和变化规律.
3.在具体情境中体会用字母表示数的意义,形成初步的符号意识.
第贰章节
新课导入
新课导入
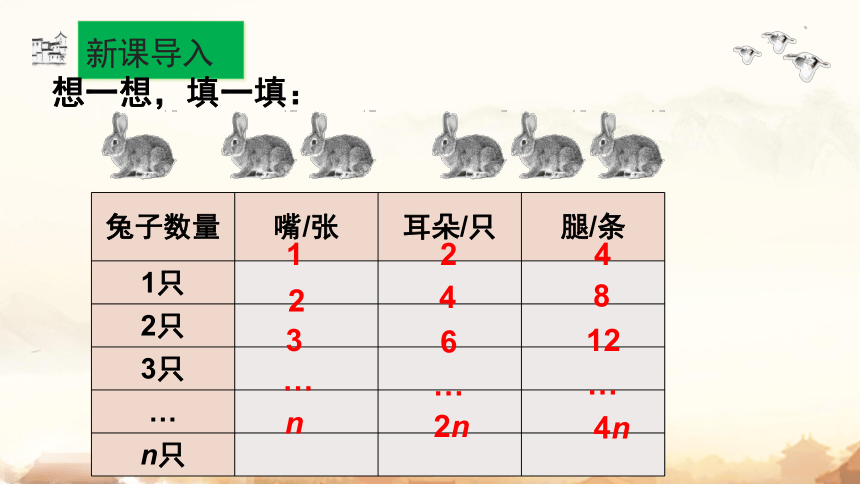
想一想,填一填:
兔子数量 嘴/张 耳朵/只 腿/条
1只
2只
3只
…
n只
1
2
4
2
4
8
3
6
12
…
…
…
n
2n
4n
第叁章节
新知探究
新知探究
用长度相同的小棒按下图所示的方式拼摆正方形。
…
(1) 按上面的方式,拼摆 2 个正方形需要____根小棒,
拼摆 3 个正方形需要____根小棒;
(2) 拼摆 5 个这样的正方形需要____根小棒。
7
10
16
用字母表示数
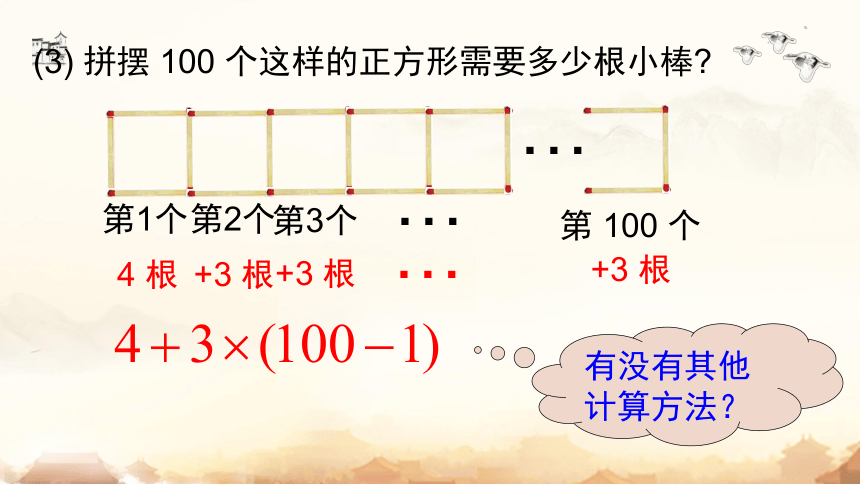
(3) 拼摆 100 个这样的正方形需要多少根小棒
第1个
4 根
第2个
第 100 个
+3 根
+3 根
…
有没有其他计算方法?
…
…
第3个
+3 根
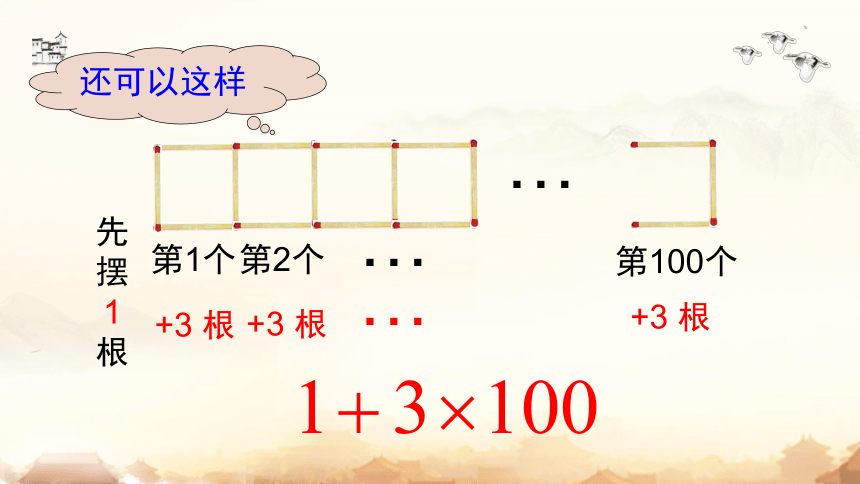
先摆 1根
第1个
+3 根
第100个
…
第2个
+3 根
+3 根
还可以这样
…
…
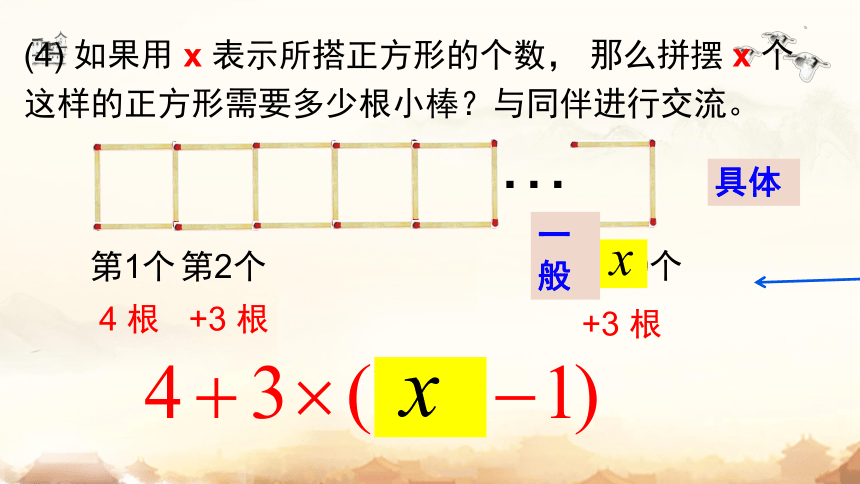
(4) 如果用 x 表示所搭正方形的个数, 那么拼摆 x 个这样的正方形需要多少根小棒?与同伴进行交流。
第1个
4 根
第2个
第100个
+3 根
+3 根
…
具体
一般
…
第1个
+3 根
第100个
第2个
+3 根
+3 根
先摆 1根
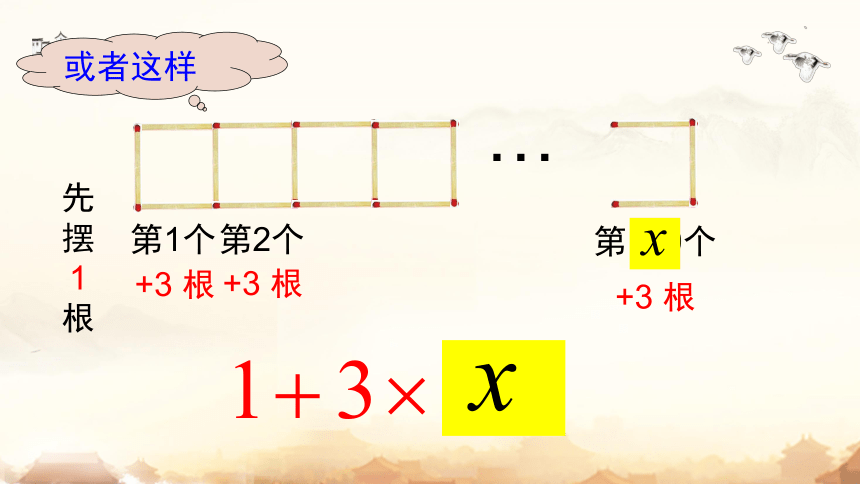
或者这样
根据你的计算方法,拼摆 200 个这样的正方形需要______根小棒; 拼摆 2024 个这样的正方形需要______根小棒。
601
6073
…
能否利用前面得到的结论?
问题:如图所示,拼摆一个正方形需要 4 根小棒。
思考·交流
(1) 在上面的活动中,我们借助字母表示正方形的个数与小棒的根数之间的关系,这样做有什么好处
用字母表示数能够更方便地表示一般规律。
表示数的字母可以作为数的“替身”参与运算,建立数与数之间的数量关系,表达数及其运算的性质,等等。
运算定律 字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a + b = b + a
(a + b) + c = a + (b + c)
ab = ba
(ab)c = a(bc)
(a + b) c = ac + bc
1. 用字母表示数的运算律
(2) 在以前的学习中还有哪些地方用到了字母 这些字母都表示什么 与同伴进行交流。
2. 用字母表示有关图形的周长和面积计算公式
名称 图形 用字母表示公式 周长(C) 面积(S )
长方形
三角形
梯形
圆
b
a
a
b
c
h
b
h
c
d
a
r
(1) 今年李华 m 岁,去年李华 岁,
5 年后李华 岁。
(2) a 个人 n 天完成一项工作,那么平均每人每天的
工作量为 。
(m - 1)
(m + 5)
书写规范
① 后面带单位的相加或相减的式子要用括号括起来。
书写规范
② 除法运算写成分数形式,即除号改为分数线。
代数式
(3) 某商店上月的收人为 a 元,本月收入比上月收入的 2 倍还多 10 元,本月收人是 元。
(4) 如果正方体的棱长是 a - 1,那么正方体的体积
是 ,表面积是 。
(2a + 10)
书写规范
③ 数字与字母相乘时,“×”通常省略不写,并把数字写在字母的前面;
(a - 1)3
6(a - 1)2
书写规范
④ 相同式子相乘时,结果需要写成幂的形式;
练一练
1. 填空
(1) a 与 b 的积的 2 倍为 ;
2ab
书写规范
⑤ 字母与字母相乘时,按字母表顺序排列。
(2) 若每斤苹果 元,则买 m 斤苹果需 元。
书写规范
⑥ 带分数与字母相乘时,把带分数化成假分数。
(3) 用式子表示数 n 的相反数。
解:数 n 的相反数是 -n。
书写规范
⑦ 当“1”与字母相乘时,“1”省略不写;
当“-1”与字母相乘时,只需在该字母前加上“-”号.
定义总结
想一想:这些式子都有什么样的特点?
4 + 3(x - 1),
x + x + (x + 1),
(m - 1),
(m + 5),
2a + 10,
(a - 1)3,
6(a - 1)2
它们都是用运算符号把数和字母连接而成的式子,
这样的式子为代数式。
单独的一个数或一个字母也是代数式。
例如,5,t 都是代数式。
例2 填空:
(1) 1 893 = 1000×___ + 100×___ + 10×____ + ;
(2) 一个四位正整数,它的千位数字是 a,百位数字是 b,十位数字是 c,个位数字是 d,则这个四位正整数可表示为 。
1
8
9
3
1000a + 100b + 10c + d
列代数式
3
例3 我国“复兴号”CR400 系列动车组列车的最高时速可达 400 km. 如果按最高时速计算,问:
(1) 60 min 可以运行多少千米
(2) t min 可以运行多少千米
解:(1) 60 min=1 h,400×1=400 (km)。
(2) t min= h,400× = (km)。
答:60 min 可以运行 400 km, t min 可以运行 km。
练一练
1. 设某数为 x,用代数式表示:
(1) 比该数的 3 倍大 1 的数;
(4) 该数的倒数与 5 的差。
(2) 该数与它的 的和;
(3) 该数与 的和的 3 倍;
列代数式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.注意:
方法总结
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式。
第肆章节
随堂练习
随堂练习
1.以下各式不是代数式的是( )
A.πa+b
B.
C.5=3+a
D.0
C
2.下列各式符合代数式书写规范的是( )
A.1x
B.2
C.0.3÷x
D.-
D
3. 某校购进单价为 a 元的排球10个,单价为 b 元的篮球5个,则一共需支付( )
A.(10a+5b) 元
B.(10a-5b) 元
C.(5a+10b) 元
D.(5a-10b) 元
A
4.三个连续的偶数,中间的数是n,则最大的数是________。
5.用代数式表示:
(1) 比k的3倍少6的数可以表示为________;
(2) x的相反数与y的和可以表示为________;
(3) m的4倍与n的差的平方可以表示为_______。
n+2
3k-6
-x+y
(4m-n)2
6.(1) 如图,铜钱是我国古代货币,外圆内方的构造彰显了数学之美。铜钱外部的圆的半径为a ,正方形孔的边长为b,用代数式表示铜钱的面积(厚度不计)。
解:铜钱的面积为πa2-b2。
6.(2) 某商场将进价为a元的 A 商品按进价提高30%确定标价,后又推出降价100元的促销活动,用代数式表示促销活动期间该商场 A 商品的售价。
解:促销活动期间该商场 A 商品的售价为(1.3a-100)元。
第伍章节
课堂小结
课堂小结
用字母表示数
用字母表示规律
用字母表示数量关系
北师大版数学七年级上册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
北师大版数学七年级上册
第三章 整式及其加减
汇报人:孙老师
汇报班级:X级X班
3.1 代数式
3.1 第1课时 代数式
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.能用字母表示运算律以及计算公式.
2. 能用字母表示一些简单问题中的数量关系和变化规律.
3.在具体情境中体会用字母表示数的意义,形成初步的符号意识.
第贰章节
新课导入
新课导入
想一想,填一填:
兔子数量 嘴/张 耳朵/只 腿/条
1只
2只
3只
…
n只
1
2
4
2
4
8
3
6
12
…
…
…
n
2n
4n
第叁章节
新知探究
新知探究
用长度相同的小棒按下图所示的方式拼摆正方形。
…
(1) 按上面的方式,拼摆 2 个正方形需要____根小棒,
拼摆 3 个正方形需要____根小棒;
(2) 拼摆 5 个这样的正方形需要____根小棒。
7
10
16
用字母表示数
(3) 拼摆 100 个这样的正方形需要多少根小棒
第1个
4 根
第2个
第 100 个
+3 根
+3 根
…
有没有其他计算方法?
…
…
第3个
+3 根
先摆 1根
第1个
+3 根
第100个
…
第2个
+3 根
+3 根
还可以这样
…
…
(4) 如果用 x 表示所搭正方形的个数, 那么拼摆 x 个这样的正方形需要多少根小棒?与同伴进行交流。
第1个
4 根
第2个
第100个
+3 根
+3 根
…
具体
一般
…
第1个
+3 根
第100个
第2个
+3 根
+3 根
先摆 1根
或者这样
根据你的计算方法,拼摆 200 个这样的正方形需要______根小棒; 拼摆 2024 个这样的正方形需要______根小棒。
601
6073
…
能否利用前面得到的结论?
问题:如图所示,拼摆一个正方形需要 4 根小棒。
思考·交流
(1) 在上面的活动中,我们借助字母表示正方形的个数与小棒的根数之间的关系,这样做有什么好处
用字母表示数能够更方便地表示一般规律。
表示数的字母可以作为数的“替身”参与运算,建立数与数之间的数量关系,表达数及其运算的性质,等等。
运算定律 字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a + b = b + a
(a + b) + c = a + (b + c)
ab = ba
(ab)c = a(bc)
(a + b) c = ac + bc
1. 用字母表示数的运算律
(2) 在以前的学习中还有哪些地方用到了字母 这些字母都表示什么 与同伴进行交流。
2. 用字母表示有关图形的周长和面积计算公式
名称 图形 用字母表示公式 周长(C) 面积(S )
长方形
三角形
梯形
圆
b
a
a
b
c
h
b
h
c
d
a
r
(1) 今年李华 m 岁,去年李华 岁,
5 年后李华 岁。
(2) a 个人 n 天完成一项工作,那么平均每人每天的
工作量为 。
(m - 1)
(m + 5)
书写规范
① 后面带单位的相加或相减的式子要用括号括起来。
书写规范
② 除法运算写成分数形式,即除号改为分数线。
代数式
(3) 某商店上月的收人为 a 元,本月收入比上月收入的 2 倍还多 10 元,本月收人是 元。
(4) 如果正方体的棱长是 a - 1,那么正方体的体积
是 ,表面积是 。
(2a + 10)
书写规范
③ 数字与字母相乘时,“×”通常省略不写,并把数字写在字母的前面;
(a - 1)3
6(a - 1)2
书写规范
④ 相同式子相乘时,结果需要写成幂的形式;
练一练
1. 填空
(1) a 与 b 的积的 2 倍为 ;
2ab
书写规范
⑤ 字母与字母相乘时,按字母表顺序排列。
(2) 若每斤苹果 元,则买 m 斤苹果需 元。
书写规范
⑥ 带分数与字母相乘时,把带分数化成假分数。
(3) 用式子表示数 n 的相反数。
解:数 n 的相反数是 -n。
书写规范
⑦ 当“1”与字母相乘时,“1”省略不写;
当“-1”与字母相乘时,只需在该字母前加上“-”号.
定义总结
想一想:这些式子都有什么样的特点?
4 + 3(x - 1),
x + x + (x + 1),
(m - 1),
(m + 5),
2a + 10,
(a - 1)3,
6(a - 1)2
它们都是用运算符号把数和字母连接而成的式子,
这样的式子为代数式。
单独的一个数或一个字母也是代数式。
例如,5,t 都是代数式。
例2 填空:
(1) 1 893 = 1000×___ + 100×___ + 10×____ + ;
(2) 一个四位正整数,它的千位数字是 a,百位数字是 b,十位数字是 c,个位数字是 d,则这个四位正整数可表示为 。
1
8
9
3
1000a + 100b + 10c + d
列代数式
3
例3 我国“复兴号”CR400 系列动车组列车的最高时速可达 400 km. 如果按最高时速计算,问:
(1) 60 min 可以运行多少千米
(2) t min 可以运行多少千米
解:(1) 60 min=1 h,400×1=400 (km)。
(2) t min= h,400× = (km)。
答:60 min 可以运行 400 km, t min 可以运行 km。
练一练
1. 设某数为 x,用代数式表示:
(1) 比该数的 3 倍大 1 的数;
(4) 该数的倒数与 5 的差。
(2) 该数与它的 的和;
(3) 该数与 的和的 3 倍;
列代数式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.注意:
方法总结
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式。
第肆章节
随堂练习
随堂练习
1.以下各式不是代数式的是( )
A.πa+b
B.
C.5=3+a
D.0
C
2.下列各式符合代数式书写规范的是( )
A.1x
B.2
C.0.3÷x
D.-
D
3. 某校购进单价为 a 元的排球10个,单价为 b 元的篮球5个,则一共需支付( )
A.(10a+5b) 元
B.(10a-5b) 元
C.(5a+10b) 元
D.(5a-10b) 元
A
4.三个连续的偶数,中间的数是n,则最大的数是________。
5.用代数式表示:
(1) 比k的3倍少6的数可以表示为________;
(2) x的相反数与y的和可以表示为________;
(3) m的4倍与n的差的平方可以表示为_______。
n+2
3k-6
-x+y
(4m-n)2
6.(1) 如图,铜钱是我国古代货币,外圆内方的构造彰显了数学之美。铜钱外部的圆的半径为a ,正方形孔的边长为b,用代数式表示铜钱的面积(厚度不计)。
解:铜钱的面积为πa2-b2。
6.(2) 某商场将进价为a元的 A 商品按进价提高30%确定标价,后又推出降价100元的促销活动,用代数式表示促销活动期间该商场 A 商品的售价。
解:促销活动期间该商场 A 商品的售价为(1.3a-100)元。
第伍章节
课堂小结
课堂小结
用字母表示数
用字母表示规律
用字母表示数量关系
北师大版数学七年级上册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
同课章节目录
