3.2 第3课时 整式的加减 课件(共31张PPT)
文档属性
| 名称 | 3.2 第3课时 整式的加减 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 11.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 20:21:44 | ||
图片预览





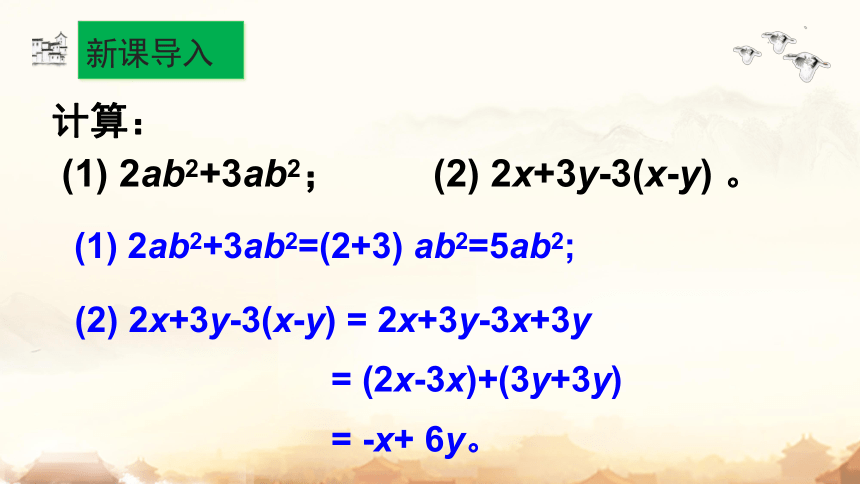






文档简介
(共31张PPT)
北师大版数学七年级上册
第三章 整式及其加减
汇报人:孙老师
汇报班级:X级X班
3.2 整式的加减
3.2 第3课时 整式的加减
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.理解整式的加减运算是建立在数的运算基础上的,数的运算律及运算法则在整式加减运算中仍然成
立,体会“数式通性”,感悟数学结论的一般性.
2.能够进行简单的整式加减运算、化简求值.
第贰章节
新课导入
新课导入
计算:
(1) 2ab2+3ab2;
(2) 2x+3y-3(x-y) 。
(1) 2ab2+3ab2=(2+3) ab2=5ab2;
(2) 2x+3y-3(x-y) = 2x+3y-3x+3y
= (2x-3x)+(3y+3y)
= -x+ 6y。
第叁章节
新知探究
新知探究
如果用 a,b 分别表示一个两位数的十位数字和个位数字,那么这个两位数可以表示为: 。交换这个两位数的十位数字和个位数字,得到的数是: 。
将这两个数相加可得:
10a + b
10b + a
整式的加减运算
1
(10a + b) + (10b + a)
= 10a + b + 10b + a
= (10a + a) + (10b + b)
= 11a + 11b
= 11(a + b)
原来不管个位和十位上的数字是几,这两个数字之和肯定是 11 的倍数,结果不变。
游戏 2:请同学在纸片上写一个两位数,交换各位上的数与十位上的数得到一个新数,将这两个数之差除以原数个位与十位的数字的差,结果是否也不变?
比如:(15 - 51)÷(1 - 5)
类比游戏
将这两个数相减可得:
(10a + b) - (10b + a)
= 10a + b - 10b - a
= (10a - a) + (b - 10b)
= 9a - 9b
= 9(a - b)
类比探究
交换前后的两个数字:
10a + b、10b + a
这两数之差是 9 的倍数。结果依然不变。
探究:在上面的探究过程中,分别涉及了整式的什么运算?说说你是如何运算的?
整式的加减运算
去括号
合并同类项
进行整式加减运算时,如果遇到括号要先 ,再 。
整式的加减运算法则:
去括号
合并同类项
知识要点
任意写一个三位数,交换它的百位数字与个位数字,又得到一个数,两个数相减。(例如:728 - 827 = -99)
两个数相减后的结果有什么规律?这个规律对任意一个三位数都成立吗?
独立探究
设原数:100a + 10b + c,
交换后的数:100c + 10b + a。
(100a + 10b + c) - (100c + 10b + a)
= 100a + 10b + c - 100c - 10b - a
= 99a - 99c
= 99(a - c)。
解:(1) (2x2-3x+1)+(-3x2+5x-7)
=2x2-3x+1-3x2+5x-7
=2x2-3x2-3x+5x+1-7
=-x2+2x-6.
典例精析
例1 计算:
(1) 2x2-3x+1 与 -3x2+5x-7 的和;
(2) 与 的差。
练一练
1. 已知多项式 3x4-5x2-3 与另一个多项式的差为 2x2-x3-5+3x4,求另一个多项式。
解:设这个多项式为 A,则由题意得
(3x4-5x2-3)-A=2x2-x3-5+3x4。
所以 A=(3x4-5x2-3)-(2x2-x3-5+3x4)
=3x4-5x2-3-2x2+x3+5-3x4
=(3-3)x4+x3+(-5-2)x2+(-3+5)
=x3-7x2+2。
2. 已知 A=-6x2+4x,B=-x2-3x,C=5x2-7x+1,小明和小白在计算时对 x 分别取了不同的数值,并进行了多次计算,但所得 A-B+C 的结果却是一样的.你认为这可能吗?说明你的理由.
理由:A-B+C
=(-6x2+4x)-(-x2-3x)+(5x2-7x+1)
=-6x2+4x+x2+3x+5x2-7x+1
=1。
解:可能。
由于结果中不含 x,所以不论 x 取何值,A-B+C的值都是 1。
例2 做大小两个长方体纸盒,尺寸如下 (单位:cm)
长 宽 高
小纸盒 a b c
大纸盒 1.5a 2b 2c
(1) 做这两个纸盒共用料多少平方厘米?
(2) 做大纸盒比做小纸盒多用料多少平方厘米?
典例精析
长方体表面积 = 2×长×宽 + 2×宽×高 + 2×长×高
解:小纸盒的表面积是 (2ab + 2bc + 2ca) cm2,
大纸盒的表面积是 (6ab + 8bc + 6ca) cm2.
(1) 做这两个纸盒共用料 (单位:cm2)
(2ab + 2bc + 2ca) + (6ab + 8bc + 6ca)
= 2ab + 2bc + 2ca + 6ab + 8bc + 6ca
= 8ab + 10bc + 8ca。
(2) 做大纸盒比做小纸盒多用料 (单位:cm2)
(6ab + 8bc + 6ac) - (2ab + 2bc + 2ca)
= 6ab + 8bc + 6ca - 2ab - 2bc - 2ca
= 4ab + 6bc + 4ac。
( )
不要忘记括号哦!
练一练
3. (渭南期末)
一个菜地共占地 (6m + 2n) 亩,其中 (3m + 6n) 亩种植白
菜,种植黄瓜的地是种植白菜的地的 ,剩下的地种植时令蔬菜,则种植时令蔬菜的地有 亩。
时令蔬菜:(6m + 2n) - (3m + 6n) - (m + 2n) = 2m - 6n
分析:黄瓜: ×(3m + 6n) = m + 2n,
(2m - 6n)
第肆章节
随堂练习
随堂练习
1.计算(3x+2)-2(2x+1)的结果是( )
A. x+3
B. -x+3
C. x
D. -x
D
2. 3a+2与5a2-3a-5 的和是 ( )
A. 5a-3
B. 5a2-6a-3
C. 5a2-3
D. 5a2+3
C
3. 若多项式(2x2+ay+6)-(3x2-y)化简后的结果不含字母 y,则a的值为_____。
-1
4.计算:
(1) (5a+3b)+(-2a+4b);
(2) 3(ab-2b2)-2(3a2-ab);
(3) -(3a2-ab-6b2)+3(a2+ab-2b2)。
解:(1)原式= 5a+3b-2a+4b
= 5a-2a+3b+4b
= 3a+7b;
(2)原式= 3ab-6b2-6a2+2ab
= -6a2+3ab+2ab-6b2
= -6a2+5ab-6b2;
4.计算:
(1) (5a+3b)+(-2a+4b);
(2) 3(ab-2b2)-2(3a2-ab);
(3) -(3a2-ab-6b2)+3(a2+ab-2b2)。
(3)原式 = -3a2+ab+6b2+3a2+3ab-6b2
= -3a2+3a2+ab+3ab+6b2-6b2
= 4ab 。
5.先化简,再求值:x-2( x- y2)+( x+ y2),
其中x=-2,y= 。
解:原式= x - x+ y2 x+ y2
当 x=-2,y= 时,
= -x+y2
原式=-(-2)+()2= 。
6.某学校开展了火箭模型制作比赛。如图为火箭模型的截面图(单位:cm),下面是梯形,中间是长方形,上面是三角形。求该截面的面积。
解:ab+a·2a+(a+2a)b
= (2a2+2ab) cm2
因此,该截面的面积为 (2a2+2ab) cm2。
第伍章节
课堂小结
课堂小结
整式加减的步骤
整式加减的应用
整式的加减
①去括号
②合并同类项
北师大版数学七年级上册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
北师大版数学七年级上册
第三章 整式及其加减
汇报人:孙老师
汇报班级:X级X班
3.2 整式的加减
3.2 第3课时 整式的加减
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.理解整式的加减运算是建立在数的运算基础上的,数的运算律及运算法则在整式加减运算中仍然成
立,体会“数式通性”,感悟数学结论的一般性.
2.能够进行简单的整式加减运算、化简求值.
第贰章节
新课导入
新课导入
计算:
(1) 2ab2+3ab2;
(2) 2x+3y-3(x-y) 。
(1) 2ab2+3ab2=(2+3) ab2=5ab2;
(2) 2x+3y-3(x-y) = 2x+3y-3x+3y
= (2x-3x)+(3y+3y)
= -x+ 6y。
第叁章节
新知探究
新知探究
如果用 a,b 分别表示一个两位数的十位数字和个位数字,那么这个两位数可以表示为: 。交换这个两位数的十位数字和个位数字,得到的数是: 。
将这两个数相加可得:
10a + b
10b + a
整式的加减运算
1
(10a + b) + (10b + a)
= 10a + b + 10b + a
= (10a + a) + (10b + b)
= 11a + 11b
= 11(a + b)
原来不管个位和十位上的数字是几,这两个数字之和肯定是 11 的倍数,结果不变。
游戏 2:请同学在纸片上写一个两位数,交换各位上的数与十位上的数得到一个新数,将这两个数之差除以原数个位与十位的数字的差,结果是否也不变?
比如:(15 - 51)÷(1 - 5)
类比游戏
将这两个数相减可得:
(10a + b) - (10b + a)
= 10a + b - 10b - a
= (10a - a) + (b - 10b)
= 9a - 9b
= 9(a - b)
类比探究
交换前后的两个数字:
10a + b、10b + a
这两数之差是 9 的倍数。结果依然不变。
探究:在上面的探究过程中,分别涉及了整式的什么运算?说说你是如何运算的?
整式的加减运算
去括号
合并同类项
进行整式加减运算时,如果遇到括号要先 ,再 。
整式的加减运算法则:
去括号
合并同类项
知识要点
任意写一个三位数,交换它的百位数字与个位数字,又得到一个数,两个数相减。(例如:728 - 827 = -99)
两个数相减后的结果有什么规律?这个规律对任意一个三位数都成立吗?
独立探究
设原数:100a + 10b + c,
交换后的数:100c + 10b + a。
(100a + 10b + c) - (100c + 10b + a)
= 100a + 10b + c - 100c - 10b - a
= 99a - 99c
= 99(a - c)。
解:(1) (2x2-3x+1)+(-3x2+5x-7)
=2x2-3x+1-3x2+5x-7
=2x2-3x2-3x+5x+1-7
=-x2+2x-6.
典例精析
例1 计算:
(1) 2x2-3x+1 与 -3x2+5x-7 的和;
(2) 与 的差。
练一练
1. 已知多项式 3x4-5x2-3 与另一个多项式的差为 2x2-x3-5+3x4,求另一个多项式。
解:设这个多项式为 A,则由题意得
(3x4-5x2-3)-A=2x2-x3-5+3x4。
所以 A=(3x4-5x2-3)-(2x2-x3-5+3x4)
=3x4-5x2-3-2x2+x3+5-3x4
=(3-3)x4+x3+(-5-2)x2+(-3+5)
=x3-7x2+2。
2. 已知 A=-6x2+4x,B=-x2-3x,C=5x2-7x+1,小明和小白在计算时对 x 分别取了不同的数值,并进行了多次计算,但所得 A-B+C 的结果却是一样的.你认为这可能吗?说明你的理由.
理由:A-B+C
=(-6x2+4x)-(-x2-3x)+(5x2-7x+1)
=-6x2+4x+x2+3x+5x2-7x+1
=1。
解:可能。
由于结果中不含 x,所以不论 x 取何值,A-B+C的值都是 1。
例2 做大小两个长方体纸盒,尺寸如下 (单位:cm)
长 宽 高
小纸盒 a b c
大纸盒 1.5a 2b 2c
(1) 做这两个纸盒共用料多少平方厘米?
(2) 做大纸盒比做小纸盒多用料多少平方厘米?
典例精析
长方体表面积 = 2×长×宽 + 2×宽×高 + 2×长×高
解:小纸盒的表面积是 (2ab + 2bc + 2ca) cm2,
大纸盒的表面积是 (6ab + 8bc + 6ca) cm2.
(1) 做这两个纸盒共用料 (单位:cm2)
(2ab + 2bc + 2ca) + (6ab + 8bc + 6ca)
= 2ab + 2bc + 2ca + 6ab + 8bc + 6ca
= 8ab + 10bc + 8ca。
(2) 做大纸盒比做小纸盒多用料 (单位:cm2)
(6ab + 8bc + 6ac) - (2ab + 2bc + 2ca)
= 6ab + 8bc + 6ca - 2ab - 2bc - 2ca
= 4ab + 6bc + 4ac。
( )
不要忘记括号哦!
练一练
3. (渭南期末)
一个菜地共占地 (6m + 2n) 亩,其中 (3m + 6n) 亩种植白
菜,种植黄瓜的地是种植白菜的地的 ,剩下的地种植时令蔬菜,则种植时令蔬菜的地有 亩。
时令蔬菜:(6m + 2n) - (3m + 6n) - (m + 2n) = 2m - 6n
分析:黄瓜: ×(3m + 6n) = m + 2n,
(2m - 6n)
第肆章节
随堂练习
随堂练习
1.计算(3x+2)-2(2x+1)的结果是( )
A. x+3
B. -x+3
C. x
D. -x
D
2. 3a+2与5a2-3a-5 的和是 ( )
A. 5a-3
B. 5a2-6a-3
C. 5a2-3
D. 5a2+3
C
3. 若多项式(2x2+ay+6)-(3x2-y)化简后的结果不含字母 y,则a的值为_____。
-1
4.计算:
(1) (5a+3b)+(-2a+4b);
(2) 3(ab-2b2)-2(3a2-ab);
(3) -(3a2-ab-6b2)+3(a2+ab-2b2)。
解:(1)原式= 5a+3b-2a+4b
= 5a-2a+3b+4b
= 3a+7b;
(2)原式= 3ab-6b2-6a2+2ab
= -6a2+3ab+2ab-6b2
= -6a2+5ab-6b2;
4.计算:
(1) (5a+3b)+(-2a+4b);
(2) 3(ab-2b2)-2(3a2-ab);
(3) -(3a2-ab-6b2)+3(a2+ab-2b2)。
(3)原式 = -3a2+ab+6b2+3a2+3ab-6b2
= -3a2+3a2+ab+3ab+6b2-6b2
= 4ab 。
5.先化简,再求值:x-2( x- y2)+( x+ y2),
其中x=-2,y= 。
解:原式= x - x+ y2 x+ y2
当 x=-2,y= 时,
= -x+y2
原式=-(-2)+()2= 。
6.某学校开展了火箭模型制作比赛。如图为火箭模型的截面图(单位:cm),下面是梯形,中间是长方形,上面是三角形。求该截面的面积。
解:ab+a·2a+(a+2a)b
= (2a2+2ab) cm2
因此,该截面的面积为 (2a2+2ab) cm2。
第伍章节
课堂小结
课堂小结
整式加减的步骤
整式加减的应用
整式的加减
①去括号
②合并同类项
北师大版数学七年级上册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
同课章节目录
