4.1 第2课时 比较线段的长短 课件 (共34张PPT)
文档属性
| 名称 | 4.1 第2课时 比较线段的长短 课件 (共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 11.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 20:51:41 | ||
图片预览








文档简介
(共34张PPT)
北师大版数学七年级上册
第四章 基本平面图形
汇报人:孙老师
汇报班级:X级X班
4.1 线段、射线、直线
4.1 第2课时 比较线段的长短
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
结合图形认识线段之间的数量关系,学会比较线段的长短.
能够用尺规作一条与已知线段相等的线段.
3. 了解“两点之间线段最短”的基本事实,知道两点间的距离,理解中点的含义.
4. 初步应用空间与图形的知识解释生活中的现象以及解决简单的实际问题,体会研究几何图形的意义.
第贰章节
新课导入
新课导入
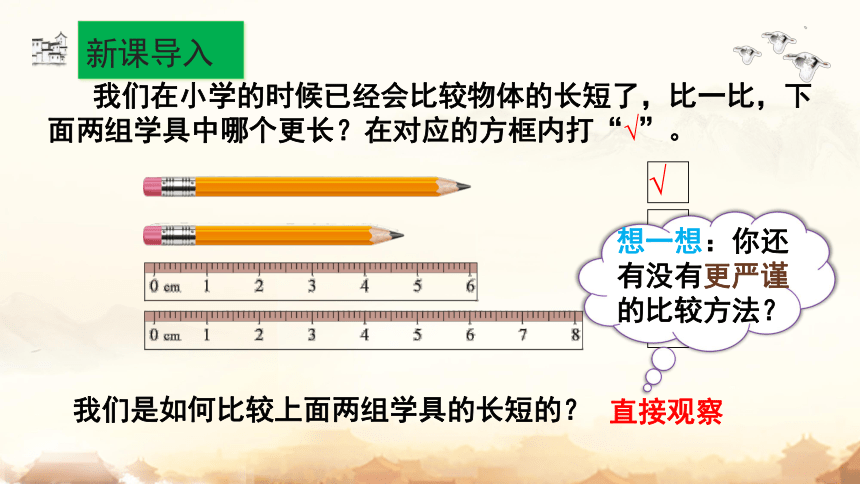
我们在小学的时候已经会比较物体的长短了,比一比,下面两组学具中哪个更长?在对应的方框内打“√”。
√
√
我们是如何比较上面两组学具的长短的?
直接观察
想一想:你还有没有更严谨的比较方法?
第叁章节
新知探究
新知探究
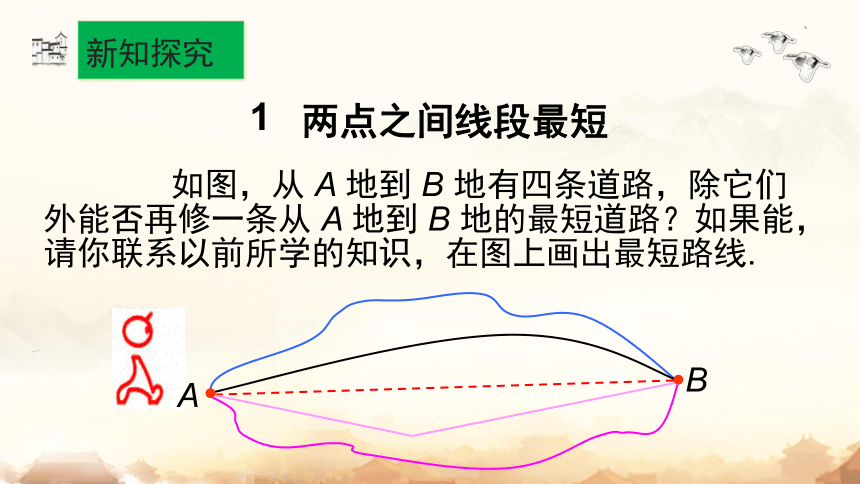
如图,从 A 地到 B 地有四条道路,除它们外能否再修一条从 A 地到 B 地的最短道路?如果能,请你联系以前所学的知识,在图上画出最短路线.
A
B
两点之间线段最短
1
归纳总结
根据生活经验,我们发现:
两点之间的所有连线中,线段最短。
我们把两点之间线段的长度,叫作
这两点之间的距离。
这一事实可以简述为:两点之间线段最短。
A
B
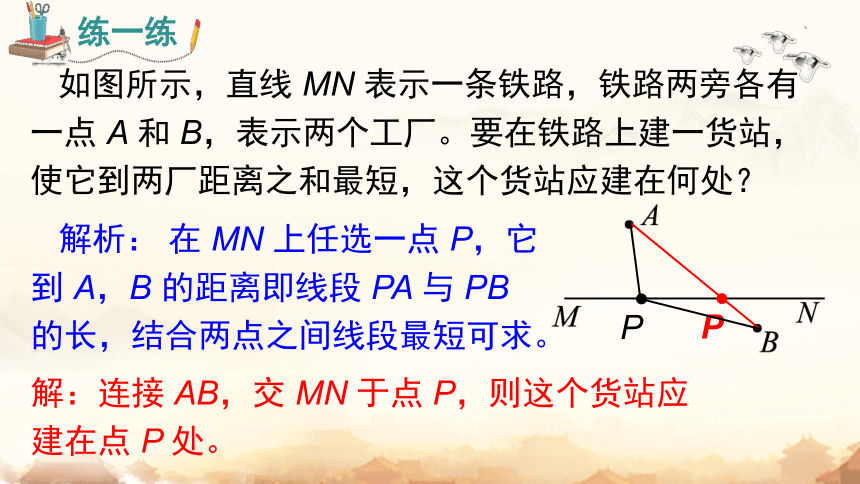
解析: 在 MN 上任选一点 P,它到 A,B 的距离即线段 PA 与 PB 的长,结合两点之间线段最短可求。
如图所示,直线 MN 表示一条铁路,铁路两旁各有一点 A 和 B,表示两个工厂。要在铁路上建一货站,使它到两厂距离之和最短,这个货站应建在何处?
解:连接 AB,交 MN 于点 P,则这个货站应建在点 P 处。
P
P
练一练
思考·交流
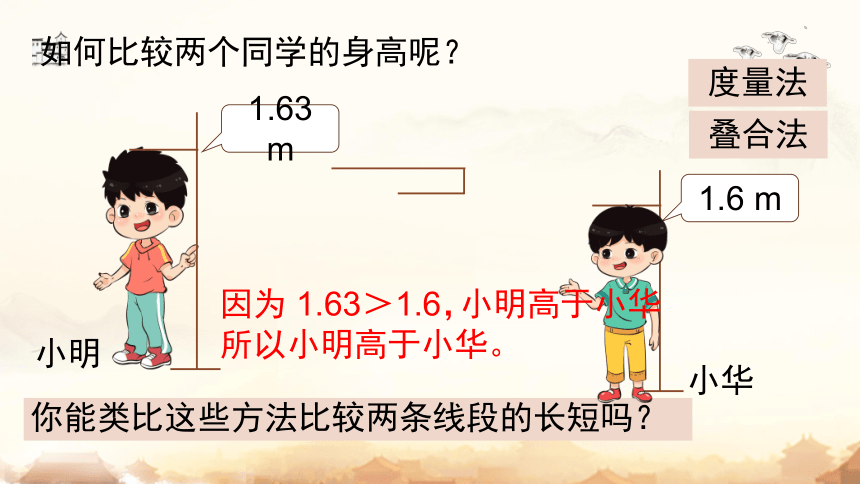
如何比较两个同学的身高呢?
线段长短的比较
2
如何比较两个同学的身高呢?
度量法
叠合法
1.63 m
1.6 m
你能类比这些方法比较两条线段的长短吗?
小明
小华
因为 1.63>1.6,
所以小明高于小华。
小明高于小华
探究1:你能比较下列线段的大小吗?
度量法
4 cm
5 cm
类比身高比较的叠合法,那么线段如何使用此方法?
A
B
C
D
1. 两条线段要放在同一条直线上。
2. 一个端点重合,另一个端点要放在公共端点的同侧。
用叠合法比较线段的长短时,有什么需要注意的吗?
合作探究
合作探究
想一想:只有圆规和无刻度的直尺的情况下,那么线段如何使用叠合法?
A
B
C
D
如何在线段 CD 上画出线段 AB,
并且一个端点重合,另一个端点要放在公共端点的同侧?
已知线段 a,如何作一条线段 AB,使 AB = a?
实际
本质
a
总结
“尺规作图”
先用直尺画射线,再用圆规在射线上截取已知线段。
a
B
作一条线段等于已知线段
a
A
C
本质
叠合法
A
B
C
D
如何在线段 CD 上画出线段 AB,并且一端端点重合,另一个端点要放在公共端点的同侧?
实际
(A)
B
归纳总结
叠合法比较线段的大小:
A(C)
D
B
AB>CD
AB = CD
AB<CD
A(C)
D
B
A(C)
B(D)
画一画
在一条直线上,画出线段 AB = 6 cm, BC = 4 cm。
A
C
B
6 cm
4 cm
A
C
B
6 cm
4 cm
在直线上画出线段 AB = a,再在 AB 的延长线上画线段 BC = b,线段 AC 就是 与 的和,记作 AC = . 如果在 AB 上画线段 BD = b,那么线段 AD 就是 与 的差,记作 AD = .
A
B
C
D
a + b
a - b
a
b
b
a
b
a + b
a
b
a - b
线段的和、差、倍、分
3
练一练
问题 如图,已知线段 a,求作线段 AB=2a。
a
M
B
a
A
P
AC = 2a
a
总结
如图,点 M 把线段 AB 分成相等的两条线段 AM 与 BM,点 M 叫作线段 AB 的中点。
A
a
a
M
B
M 是线段 AB 的中点。
几何语言:因为 M 是线段 AB 的中点,
所以 AM = BM = AB
(或 AB = 2AM = 2BM)。
反之也成立:因为 AM = BM = AB
(或 AB = 2AM = 2BM),
所以 M 是线段 AB 的中点。
思考 那么什么叫作三等分点?四等分点呢?
三等分点
如图,若点 M、N 是线段 AB 的三等分点,
则 AM = = = ,反过来也成立。
MN
NB
AB
1
3
四等分点
如图,若点 M、N、P 是线段 AB 的四等分点,
则 AM = = = = ,反过来也成立。
MN
NP
AB
1
4
PB
尝试·思考
在直线 l 上顺次取 A,B,C 三点,使得 AB = 4 cm,BC = 3 cm。如果点 O 是线段 AC 的中点,那么线段 AC 和 OB 的长度分别是多少
3 cm
4 cm
A
C
B
O
解:由题意,得
AC = AB + BC = 7 cm。
因为点 O 是线段 AC 的中点,
所以
OA = AC = 3.5 cm。
1
2
因为 OB = AB – OA,
所以 OB = 4 – 3.5
= 0.5 (cm)。
若 AB = 6 cm,点 C 是线段 AB 的中点,点 D 是线段 CB 的中点,问线段 AD 的长是多少
解:因为 C 是线段 AB 的中点,
因为 D 是线段 CB 的中点,
所以 AD = AC + CD = 3 + 1.5 = 4.5 (cm)。
A
C
B
D
所以 AC = CB = AB = ×6 = 3 (cm)。
所以 CD = CB = ×3 = 1.5 (cm)。
练一练
第肆章节
随堂练习
随堂练习
1.如图,比较线段a和线段b的长短,结果正确的是( )
A.a >b B.aC.a=b D.无法比较
B
2. 下列说法中错误的是( )
A. A,B两点之间的距离为5 cm
B. A,B两点之间的距离是线段AB的长
C. A,B两点之间的距离就是线段AB
D. A,B两点之间线段的长度叫作A,B 两点之间的距离
C
解:(1)因为AD=10 cm,AC=6 cm,
所以CD=AD-AC=4 cm 。
因为点B为CD的中点,
所以BD= CD=2 cm 。
3. 如图,C为线段AD上一点,点B为CD的中点,且AD=10 cm,AC=6 cm。
(1)求BD的长;
(2)若点E是AC的三等分点,且点E靠近点A,求BE的长。
所以AE= AC=2 cm。
3. 如图,C为线段AD上一点,点B为CD的中点,且AD=10 cm,AC=6 cm。
(1)求BD的长;
(2)若点E是AC的三等分点,且点E靠近点A,求BE的长。
(2)因为AC=6 cm,点E是AC的三等分点,且点E靠近点A,
因为BD=2 cm ,
所以BE=AD-AE-BD=6 cm。
第伍章节
课堂小结
课堂小结
比较线段的长短
两点之间线段最短
尺规作图
比较线段大小的方法
线段的中点
北师大版数学七年级上册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
北师大版数学七年级上册
第四章 基本平面图形
汇报人:孙老师
汇报班级:X级X班
4.1 线段、射线、直线
4.1 第2课时 比较线段的长短
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
结合图形认识线段之间的数量关系,学会比较线段的长短.
能够用尺规作一条与已知线段相等的线段.
3. 了解“两点之间线段最短”的基本事实,知道两点间的距离,理解中点的含义.
4. 初步应用空间与图形的知识解释生活中的现象以及解决简单的实际问题,体会研究几何图形的意义.
第贰章节
新课导入
新课导入
我们在小学的时候已经会比较物体的长短了,比一比,下面两组学具中哪个更长?在对应的方框内打“√”。
√
√
我们是如何比较上面两组学具的长短的?
直接观察
想一想:你还有没有更严谨的比较方法?
第叁章节
新知探究
新知探究
如图,从 A 地到 B 地有四条道路,除它们外能否再修一条从 A 地到 B 地的最短道路?如果能,请你联系以前所学的知识,在图上画出最短路线.
A
B
两点之间线段最短
1
归纳总结
根据生活经验,我们发现:
两点之间的所有连线中,线段最短。
我们把两点之间线段的长度,叫作
这两点之间的距离。
这一事实可以简述为:两点之间线段最短。
A
B
解析: 在 MN 上任选一点 P,它到 A,B 的距离即线段 PA 与 PB 的长,结合两点之间线段最短可求。
如图所示,直线 MN 表示一条铁路,铁路两旁各有一点 A 和 B,表示两个工厂。要在铁路上建一货站,使它到两厂距离之和最短,这个货站应建在何处?
解:连接 AB,交 MN 于点 P,则这个货站应建在点 P 处。
P
P
练一练
思考·交流
如何比较两个同学的身高呢?
线段长短的比较
2
如何比较两个同学的身高呢?
度量法
叠合法
1.63 m
1.6 m
你能类比这些方法比较两条线段的长短吗?
小明
小华
因为 1.63>1.6,
所以小明高于小华。
小明高于小华
探究1:你能比较下列线段的大小吗?
度量法
4 cm
5 cm
类比身高比较的叠合法,那么线段如何使用此方法?
A
B
C
D
1. 两条线段要放在同一条直线上。
2. 一个端点重合,另一个端点要放在公共端点的同侧。
用叠合法比较线段的长短时,有什么需要注意的吗?
合作探究
合作探究
想一想:只有圆规和无刻度的直尺的情况下,那么线段如何使用叠合法?
A
B
C
D
如何在线段 CD 上画出线段 AB,
并且一个端点重合,另一个端点要放在公共端点的同侧?
已知线段 a,如何作一条线段 AB,使 AB = a?
实际
本质
a
总结
“尺规作图”
先用直尺画射线,再用圆规在射线上截取已知线段。
a
B
作一条线段等于已知线段
a
A
C
本质
叠合法
A
B
C
D
如何在线段 CD 上画出线段 AB,并且一端端点重合,另一个端点要放在公共端点的同侧?
实际
(A)
B
归纳总结
叠合法比较线段的大小:
A(C)
D
B
AB>CD
AB = CD
AB<CD
A(C)
D
B
A(C)
B(D)
画一画
在一条直线上,画出线段 AB = 6 cm, BC = 4 cm。
A
C
B
6 cm
4 cm
A
C
B
6 cm
4 cm
在直线上画出线段 AB = a,再在 AB 的延长线上画线段 BC = b,线段 AC 就是 与 的和,记作 AC = . 如果在 AB 上画线段 BD = b,那么线段 AD 就是 与 的差,记作 AD = .
A
B
C
D
a + b
a - b
a
b
b
a
b
a + b
a
b
a - b
线段的和、差、倍、分
3
练一练
问题 如图,已知线段 a,求作线段 AB=2a。
a
M
B
a
A
P
AC = 2a
a
总结
如图,点 M 把线段 AB 分成相等的两条线段 AM 与 BM,点 M 叫作线段 AB 的中点。
A
a
a
M
B
M 是线段 AB 的中点。
几何语言:因为 M 是线段 AB 的中点,
所以 AM = BM = AB
(或 AB = 2AM = 2BM)。
反之也成立:因为 AM = BM = AB
(或 AB = 2AM = 2BM),
所以 M 是线段 AB 的中点。
思考 那么什么叫作三等分点?四等分点呢?
三等分点
如图,若点 M、N 是线段 AB 的三等分点,
则 AM = = = ,反过来也成立。
MN
NB
AB
1
3
四等分点
如图,若点 M、N、P 是线段 AB 的四等分点,
则 AM = = = = ,反过来也成立。
MN
NP
AB
1
4
PB
尝试·思考
在直线 l 上顺次取 A,B,C 三点,使得 AB = 4 cm,BC = 3 cm。如果点 O 是线段 AC 的中点,那么线段 AC 和 OB 的长度分别是多少
3 cm
4 cm
A
C
B
O
解:由题意,得
AC = AB + BC = 7 cm。
因为点 O 是线段 AC 的中点,
所以
OA = AC = 3.5 cm。
1
2
因为 OB = AB – OA,
所以 OB = 4 – 3.5
= 0.5 (cm)。
若 AB = 6 cm,点 C 是线段 AB 的中点,点 D 是线段 CB 的中点,问线段 AD 的长是多少
解:因为 C 是线段 AB 的中点,
因为 D 是线段 CB 的中点,
所以 AD = AC + CD = 3 + 1.5 = 4.5 (cm)。
A
C
B
D
所以 AC = CB = AB = ×6 = 3 (cm)。
所以 CD = CB = ×3 = 1.5 (cm)。
练一练
第肆章节
随堂练习
随堂练习
1.如图,比较线段a和线段b的长短,结果正确的是( )
A.a >b B.a
B
2. 下列说法中错误的是( )
A. A,B两点之间的距离为5 cm
B. A,B两点之间的距离是线段AB的长
C. A,B两点之间的距离就是线段AB
D. A,B两点之间线段的长度叫作A,B 两点之间的距离
C
解:(1)因为AD=10 cm,AC=6 cm,
所以CD=AD-AC=4 cm 。
因为点B为CD的中点,
所以BD= CD=2 cm 。
3. 如图,C为线段AD上一点,点B为CD的中点,且AD=10 cm,AC=6 cm。
(1)求BD的长;
(2)若点E是AC的三等分点,且点E靠近点A,求BE的长。
所以AE= AC=2 cm。
3. 如图,C为线段AD上一点,点B为CD的中点,且AD=10 cm,AC=6 cm。
(1)求BD的长;
(2)若点E是AC的三等分点,且点E靠近点A,求BE的长。
(2)因为AC=6 cm,点E是AC的三等分点,且点E靠近点A,
因为BD=2 cm ,
所以BE=AD-AE-BD=6 cm。
第伍章节
课堂小结
课堂小结
比较线段的长短
两点之间线段最短
尺规作图
比较线段大小的方法
线段的中点
北师大版数学七年级上册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
同课章节目录
