5.3 第1课时 形积问题 课件 (共31张PPT)
文档属性
| 名称 | 5.3 第1课时 形积问题 课件 (共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 20:55:38 | ||
图片预览










文档简介
(共31张PPT)
北师大版数学七年级上册
第五章 一元一次方程
汇报人:孙老师
汇报班级:X级X班
5.3 一元一次方程的应用
5.3 第1课时 形积问题
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1. 借助立体及平面图形学会分析复杂问题中的数量关系和等量关系,建立方程,解决实际问题.
2.通过具体问题的解决,体会利用方程解决问题的关键是寻找等量关系.
第贰章节
新课导入
新课导入
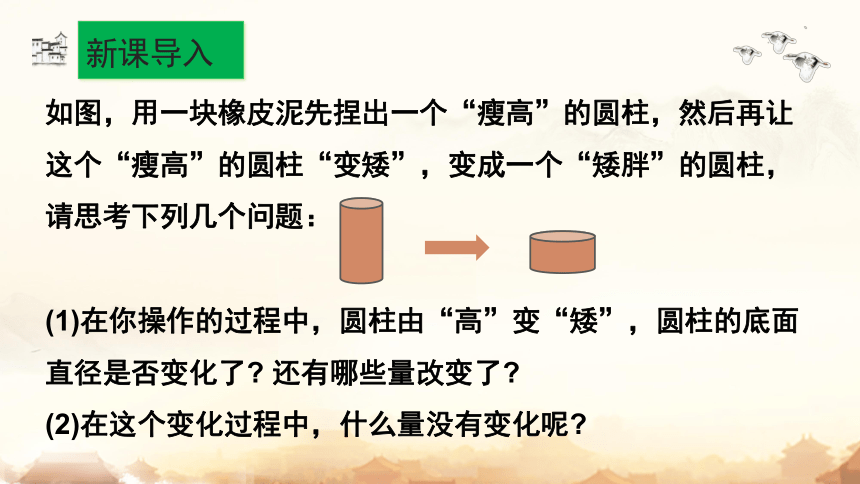
如图,用一块橡皮泥先捏出一个“瘦高”的圆柱,然后再让这个“瘦高”的圆柱“变矮”,变成一个“矮胖”的圆柱, 请思考下列几个问题:
(1)在你操作的过程中,圆柱由“高”变“矮”,圆柱的底面直径是否变化了 还有哪些量改变了
(2)在这个变化过程中,什么量没有变化呢
第叁章节
新知探究
新知探究
例1 某饮料公司有一种底面直径和高分别为 6.6 cm,
12 cm 的圆柱形易拉罐饮料。经市场调研决定对该产品外包装进行改造,计划将它的底面直径减少为 6 cm。那么在容积不变的前提下,易拉罐的高度将变为多少厘米?
(1)这个问题中包含哪些量?它们之间有怎样的等量关系?
容积=π× ×高
直径
2
2
等积变形问题
1
合作探究
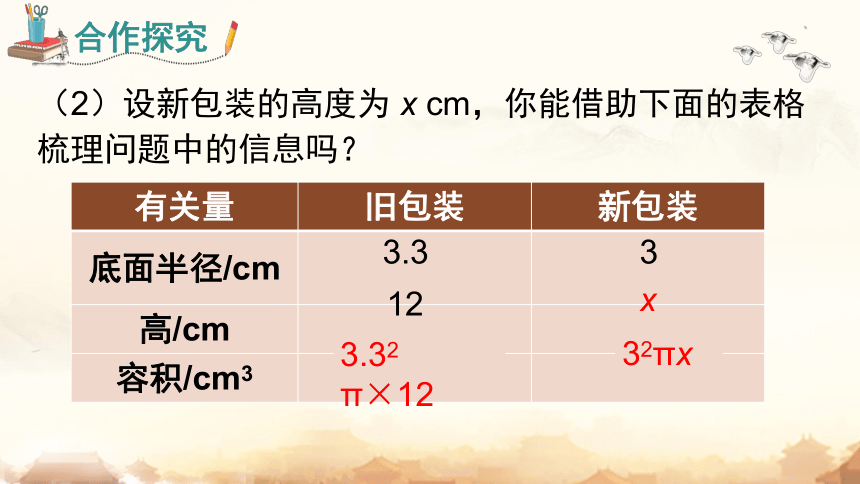
(2)设新包装的高度为 x cm,你能借助下面的表格梳理问题中的信息吗?
有关量 旧包装 新包装
底面半径/cm
高/cm
容积/cm3
12
3.3
3
x
V
V
3.32 π×12
32πx
知识总结
(3)根据等量关系,你能列出怎样的方程?
设新包装的高度为 x cm。
根据等量关系,列出方程: 。
解这个方程,得 x = 。
因此,易拉罐的高度变为 cm。
14.52
14.52
3.32π×12 = 32πx
1. 要锻造一个直径为 8 cm、高为 4 cm的圆柱形毛坯,则至少应截取直径为 4 cm 的圆钢______cm.
2. 钢锭的截面是正方形,其边长是 20 cm,要锻造成长、宽、高分别为 40 cm、30 cm、10 cm的长方体,则应截取这种钢锭多长?
答:应截取这种钢锭 30 cm.
16
练一练
方法总结
物体由一种形状变成了另一种形状,形状发生了变化,但是体积保持不变。
“变形之前物体的体积=变形之后物体的体积”就是我们所要寻找的等量关系。
(1) 如果该长方形的长比宽多 1.4 m,那么此时长方形的长、宽各为多少米?
在这个过程中什么没有发生变化?
长方形的周长(或长与宽的和)不变
用一根长为 10 m 的铁丝围成一个长方形。
等长变形问题
2
x m
(x + 1.4) m
等量关系:
(长 + 宽)× 2 = 周长
解: 设此时长方形的宽为 x m,则它的长为(x + 1.4)m. 根据题意,得
(x + 1.4 + x) ×2 = 10
解得 x = 1.8
1.8 + 1.4 = 3.2
答:此时长方形的长为 3.2 m,宽为 1.8 m.
(2) 如果该长方形的长比宽多 0.8 m,那么此时长方形的长、宽各为多少米?此时的长方形与 (1) 中的长方形相比,面积有什么变化?
x m
(x + 0.8) m
解:设此时长方形的宽为 x m,则它的长为
(x + 0.8) m. 根据题意,得
(x + 0.8 + x) ×2 = 10
解得 x = 2.1
2.1 + 0.8 = 2.9
此时长方形的长为 2.9 m,宽为 2.1 m,
面积为 2.9×2.1 = 6.09 (m2),
(1) 中长方形的面积为 3.2×1.8 = 5.76(m2).
此时长方形的面积比 (1) 中长方形的面积增大了,增大了6.09-5.76 = 0.33(m2).
(3) 如果该长方形的长与宽相等,即围成一个正方形,那么此时正方形的边长是多少米?正方形的面积与(2)中长方形的面积相比,又有什么变化?
x m
(x + x)×2 = 10
解得 x = 2.5
正方形的面积为 2.5×2.5 = 6.25(m2).
解:设正方形的边长为 x m.
根据题意,得
比(2)中面积增大 6. 25 - 6.09 = 0.16(m2).
正方形的边长为 2.5 m,
同样长的铁丝可以围更大的地方.
方法总结
思考:在上面的问题中,所列方程的两边分别表示什么量?列方程的思路是什么?与同伴进行交流。
形状、面积不同,而周长相同可根据题意列出关于周长的等量关系式。解决问题的关键是通过分析变化过程,挖掘其等量关系,从而列出方程。
练一练
1. (济南·期末) 李师傅正在准备用篱笆修建一个长方形鸡舍栅栏,栅栏一面靠墙 (墙面长度不限),三面用篱笆,篱笆总长 60 米,篱笆围成的长方形鸡舍的长比宽多 6 米,请你用所学的知识解决以下问题 (篱笆的占地面积忽略不计)。
(1) 如图,如果长方形鸡舍的长与墙为
对面,长方形鸡舍的面积是多少?
(1) 解:设鸡舍的宽为 x 米,则长为 (x + 6) 米,依题意得
x + x + 6 + x = 60,
解得 x = 18。
所以鸡舍的长为 18 + 6 = 24 (米)。
鸡舍面积 = 18×24 = 432 (平方米)。
答:鸡舍面积 432 平方米。
(2) 如果要在墙的对面留一个 3 米宽的门 (门不使用篱笆), 那么长方形鸡舍的面积又是多少?
(2) 解:设鸡舍的宽为 x 米,则鸡舍的长 (x + 6) 米。
①当鸡舍的长与墙为对面时,依题意得
x + x + (x + 6 - 3) = 60,
解得 x = 19。
鸡舍面积 = 19×(19 + 6) = 475 (平方米)。
②当鸡舍的宽与墙为对面时,依题意得
2(x + 6) + x - 3 = 60,
解得 x = 17。
鸡舍面积 = 17×(17+6) = 391 (平方米)
答:鸡舍面积为 475 平方米或 391 平方米.
第肆章节
随堂练习
随堂练习
1.两个圆柱体容器如图所示,它们的底面直径分别为4 cm和8 cm,高分别为39 cm和 10 cm. 先在右侧容器中倒满水,然后将其倒入左侧容器中. 倒完以后,左侧容器中的水面离容器口有多少厘米
小刚是这样做的:设倒完以后,左侧容器中的水面离容器口有x cm. 列方程 π×22×(39-x)= π×42×10.
解得x=-1. 请你对他的结果作出合理的解释.
【选自教材P154 习题5.3 第1题】
解:由题意可知,第一个容器的体积为
22×39×π = 156π cm2
第二个容器的体积为
42×10×π = 160π cm2
第二个容器的体积大于第一个容器的体积,因此将第二个容器装满水后再倒入第一个容器中,水会溢出,
即方程 π×22×(39-x)= π × 42×10的解小于0.
2.现有两块试验田,第一块试验田的面积比第二块试验田面
积的3倍还多100 m2,这两块试验田的面积共2900 m2,两块试验田的面积分别是多少
解:设第二块试验田的面积是 x m2,
则第一块试验田的面积是(3x + 100)m2
根据题意,得 x + 3x + 100 = 2900
解得 x = 700
所以 3x + 100 = 2200
答:第一块试验田的面积是 2200 m2,
第二块试验田的面积是 700 m2
【选自教材P154 习题5.3 第3题】
3.如图,小强将一个正方形纸片剪去一个宽为4 cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm 的长条. 如果两次剪下的长条面积正好相等,那么每一个长条的面积为多少
解:设正方形的边长为 x cm
根据题意,得 4x = 5(x - 4)
解得 x = 20
所以每一个长条的面积为 4×20 = 80(cm2)
答:每一个长条的面积为 80 cm2.
【选自教材P154 习题5.3 第4题】
4.如图,某种卷筒纸的外直径为14 cm,内直径为6 cm,每层纸的厚度为0.02 cm. 假如把这筒纸全部拉开,那么这筒纸的总长度大约是多少米(π取3.14)
【选自教材P154 习题5.3 第5题】
解:设卷筒纸的宽度为 x cm
卷筒纸的体积为 =
40πx
卷筒纸的总长度为:40πx÷0.02x≈6280(cm)=62.8(m)
答:卷筒纸的总长度为62.8m
第伍章节
课堂小结
课堂小结
几何图形中的等量关系
等积变形:
变形前体积=变形后体积
等长变形:
变形前周长=变形后周长
(长方形周长不变时,当且仅当长与宽相等时,面积最大)
列方程解决实际问题的一般步骤:
审设列解验答
注意:列方程的关键是正确找出等量关系.
北师大版数学七年级上册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
北师大版数学七年级上册
第五章 一元一次方程
汇报人:孙老师
汇报班级:X级X班
5.3 一元一次方程的应用
5.3 第1课时 形积问题
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1. 借助立体及平面图形学会分析复杂问题中的数量关系和等量关系,建立方程,解决实际问题.
2.通过具体问题的解决,体会利用方程解决问题的关键是寻找等量关系.
第贰章节
新课导入
新课导入
如图,用一块橡皮泥先捏出一个“瘦高”的圆柱,然后再让这个“瘦高”的圆柱“变矮”,变成一个“矮胖”的圆柱, 请思考下列几个问题:
(1)在你操作的过程中,圆柱由“高”变“矮”,圆柱的底面直径是否变化了 还有哪些量改变了
(2)在这个变化过程中,什么量没有变化呢
第叁章节
新知探究
新知探究
例1 某饮料公司有一种底面直径和高分别为 6.6 cm,
12 cm 的圆柱形易拉罐饮料。经市场调研决定对该产品外包装进行改造,计划将它的底面直径减少为 6 cm。那么在容积不变的前提下,易拉罐的高度将变为多少厘米?
(1)这个问题中包含哪些量?它们之间有怎样的等量关系?
容积=π× ×高
直径
2
2
等积变形问题
1
合作探究
(2)设新包装的高度为 x cm,你能借助下面的表格梳理问题中的信息吗?
有关量 旧包装 新包装
底面半径/cm
高/cm
容积/cm3
12
3.3
3
x
V
V
3.32 π×12
32πx
知识总结
(3)根据等量关系,你能列出怎样的方程?
设新包装的高度为 x cm。
根据等量关系,列出方程: 。
解这个方程,得 x = 。
因此,易拉罐的高度变为 cm。
14.52
14.52
3.32π×12 = 32πx
1. 要锻造一个直径为 8 cm、高为 4 cm的圆柱形毛坯,则至少应截取直径为 4 cm 的圆钢______cm.
2. 钢锭的截面是正方形,其边长是 20 cm,要锻造成长、宽、高分别为 40 cm、30 cm、10 cm的长方体,则应截取这种钢锭多长?
答:应截取这种钢锭 30 cm.
16
练一练
方法总结
物体由一种形状变成了另一种形状,形状发生了变化,但是体积保持不变。
“变形之前物体的体积=变形之后物体的体积”就是我们所要寻找的等量关系。
(1) 如果该长方形的长比宽多 1.4 m,那么此时长方形的长、宽各为多少米?
在这个过程中什么没有发生变化?
长方形的周长(或长与宽的和)不变
用一根长为 10 m 的铁丝围成一个长方形。
等长变形问题
2
x m
(x + 1.4) m
等量关系:
(长 + 宽)× 2 = 周长
解: 设此时长方形的宽为 x m,则它的长为(x + 1.4)m. 根据题意,得
(x + 1.4 + x) ×2 = 10
解得 x = 1.8
1.8 + 1.4 = 3.2
答:此时长方形的长为 3.2 m,宽为 1.8 m.
(2) 如果该长方形的长比宽多 0.8 m,那么此时长方形的长、宽各为多少米?此时的长方形与 (1) 中的长方形相比,面积有什么变化?
x m
(x + 0.8) m
解:设此时长方形的宽为 x m,则它的长为
(x + 0.8) m. 根据题意,得
(x + 0.8 + x) ×2 = 10
解得 x = 2.1
2.1 + 0.8 = 2.9
此时长方形的长为 2.9 m,宽为 2.1 m,
面积为 2.9×2.1 = 6.09 (m2),
(1) 中长方形的面积为 3.2×1.8 = 5.76(m2).
此时长方形的面积比 (1) 中长方形的面积增大了,增大了6.09-5.76 = 0.33(m2).
(3) 如果该长方形的长与宽相等,即围成一个正方形,那么此时正方形的边长是多少米?正方形的面积与(2)中长方形的面积相比,又有什么变化?
x m
(x + x)×2 = 10
解得 x = 2.5
正方形的面积为 2.5×2.5 = 6.25(m2).
解:设正方形的边长为 x m.
根据题意,得
比(2)中面积增大 6. 25 - 6.09 = 0.16(m2).
正方形的边长为 2.5 m,
同样长的铁丝可以围更大的地方.
方法总结
思考:在上面的问题中,所列方程的两边分别表示什么量?列方程的思路是什么?与同伴进行交流。
形状、面积不同,而周长相同可根据题意列出关于周长的等量关系式。解决问题的关键是通过分析变化过程,挖掘其等量关系,从而列出方程。
练一练
1. (济南·期末) 李师傅正在准备用篱笆修建一个长方形鸡舍栅栏,栅栏一面靠墙 (墙面长度不限),三面用篱笆,篱笆总长 60 米,篱笆围成的长方形鸡舍的长比宽多 6 米,请你用所学的知识解决以下问题 (篱笆的占地面积忽略不计)。
(1) 如图,如果长方形鸡舍的长与墙为
对面,长方形鸡舍的面积是多少?
(1) 解:设鸡舍的宽为 x 米,则长为 (x + 6) 米,依题意得
x + x + 6 + x = 60,
解得 x = 18。
所以鸡舍的长为 18 + 6 = 24 (米)。
鸡舍面积 = 18×24 = 432 (平方米)。
答:鸡舍面积 432 平方米。
(2) 如果要在墙的对面留一个 3 米宽的门 (门不使用篱笆), 那么长方形鸡舍的面积又是多少?
(2) 解:设鸡舍的宽为 x 米,则鸡舍的长 (x + 6) 米。
①当鸡舍的长与墙为对面时,依题意得
x + x + (x + 6 - 3) = 60,
解得 x = 19。
鸡舍面积 = 19×(19 + 6) = 475 (平方米)。
②当鸡舍的宽与墙为对面时,依题意得
2(x + 6) + x - 3 = 60,
解得 x = 17。
鸡舍面积 = 17×(17+6) = 391 (平方米)
答:鸡舍面积为 475 平方米或 391 平方米.
第肆章节
随堂练习
随堂练习
1.两个圆柱体容器如图所示,它们的底面直径分别为4 cm和8 cm,高分别为39 cm和 10 cm. 先在右侧容器中倒满水,然后将其倒入左侧容器中. 倒完以后,左侧容器中的水面离容器口有多少厘米
小刚是这样做的:设倒完以后,左侧容器中的水面离容器口有x cm. 列方程 π×22×(39-x)= π×42×10.
解得x=-1. 请你对他的结果作出合理的解释.
【选自教材P154 习题5.3 第1题】
解:由题意可知,第一个容器的体积为
22×39×π = 156π cm2
第二个容器的体积为
42×10×π = 160π cm2
第二个容器的体积大于第一个容器的体积,因此将第二个容器装满水后再倒入第一个容器中,水会溢出,
即方程 π×22×(39-x)= π × 42×10的解小于0.
2.现有两块试验田,第一块试验田的面积比第二块试验田面
积的3倍还多100 m2,这两块试验田的面积共2900 m2,两块试验田的面积分别是多少
解:设第二块试验田的面积是 x m2,
则第一块试验田的面积是(3x + 100)m2
根据题意,得 x + 3x + 100 = 2900
解得 x = 700
所以 3x + 100 = 2200
答:第一块试验田的面积是 2200 m2,
第二块试验田的面积是 700 m2
【选自教材P154 习题5.3 第3题】
3.如图,小强将一个正方形纸片剪去一个宽为4 cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm 的长条. 如果两次剪下的长条面积正好相等,那么每一个长条的面积为多少
解:设正方形的边长为 x cm
根据题意,得 4x = 5(x - 4)
解得 x = 20
所以每一个长条的面积为 4×20 = 80(cm2)
答:每一个长条的面积为 80 cm2.
【选自教材P154 习题5.3 第4题】
4.如图,某种卷筒纸的外直径为14 cm,内直径为6 cm,每层纸的厚度为0.02 cm. 假如把这筒纸全部拉开,那么这筒纸的总长度大约是多少米(π取3.14)
【选自教材P154 习题5.3 第5题】
解:设卷筒纸的宽度为 x cm
卷筒纸的体积为 =
40πx
卷筒纸的总长度为:40πx÷0.02x≈6280(cm)=62.8(m)
答:卷筒纸的总长度为62.8m
第伍章节
课堂小结
课堂小结
几何图形中的等量关系
等积变形:
变形前体积=变形后体积
等长变形:
变形前周长=变形后周长
(长方形周长不变时,当且仅当长与宽相等时,面积最大)
列方程解决实际问题的一般步骤:
审设列解验答
注意:列方程的关键是正确找出等量关系.
北师大版数学七年级上册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
同课章节目录
