(期末冲刺)2024-2025学年五年级数学下册常考易错提升试卷(人教版)(含解析)
文档属性
| 名称 | (期末冲刺)2024-2025学年五年级数学下册常考易错提升试卷(人教版)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 324.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 16:51:30 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
(期末冲刺)2024-2025学年五年级数学下册常考易错提升试卷(人教版)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.一个长方体游泳池,长25米,宽15米,深1.5米,这个游泳池占地( )平方米。
A.750 B.375 C.27
2.实验小学的学生们参加科技小制作比赛,其中有的人获得一等奖,有的人获得二等奖,有的人获得三等奖,其余的人获得优秀奖,该校可能有( )人参加科技小制作比赛。
A.24 B.30 C.36 D.50
3.一个数的最小倍数一定( )它本身。
A.等于 B.大于 C.小于
4.一罐可口可乐的容量是( )
A.355米3 B.355毫升 C.355分米3
5.一个长方体的长、宽、高都扩大到原来的3倍,它的体积扩大到原来的( )。
A.27倍 B.9倍 C.3倍
6.一个两位数是3的倍数,这个两位数最大可能是( )。
A.90 B.99 C.98 D.100
二、填空题
7.被除数相当于分数的( ),除数相当于分数的( ),除号相当于( ),商相当于( )。
8.在2、9、13、19、87、1、201、3、0、54中,偶数有( ),奇数有( ),质数有( ),合数有( )。
9.下面每组中的两个分数是否相等?相等的画“√”,不相等的画“×”。
和( ) 和( ) 和( )
10.用三个棱长都是2cm的正方体拼成一个长方体,这个长方体的表面积是( )cm2,体积是( )cm3。
11.一个正方体的棱长变为原来的4倍,则它的棱长和变为原来的( )倍,表面积变为原来的( )倍,体积变为原来的( )倍。
12.盒子里面有15块同样的蛋糕,青青吃了,这里把( )看作单位“1”,把它平均分成( )份,青青吃了( )份,共吃了( )块。
13.用同样的正方体积木搭几何体,要求从正面、上面和左面看到的图形都是,搭这样的几何体,最少需要( )块正方体积木,最多需要( )块。
14.有一个学生无意间将中间的两个5划去得,他惊讶地发现这两个分数居然相等。这是偶然的吗?他进行了研究,发现这样的分数还有很多,请你也写出一个类似这样的分数 。
三、判断题
15.一个自然数不是奇数就是偶数。( )
16.3的倍数都是奇数。( )
17.一个两位数,十位上是8,它一定是2的倍数。 ( )
18.从不同的位置观察物体,所看到的形状完全相同。( )
19.因为19和35是互质数,所以19和35没有公因数。 。
20.所有的质数加上1后,就变成了合数. ( )
四、计算题
21.直接写出得数。
+= -= 7.2÷0.6= 1-= 1.5×7+1.5×3= +=
7.5×0.8= += += -= ++= 103=
22.计算下面各题,能简算的要简算。
(1) (2)
(3) (4)
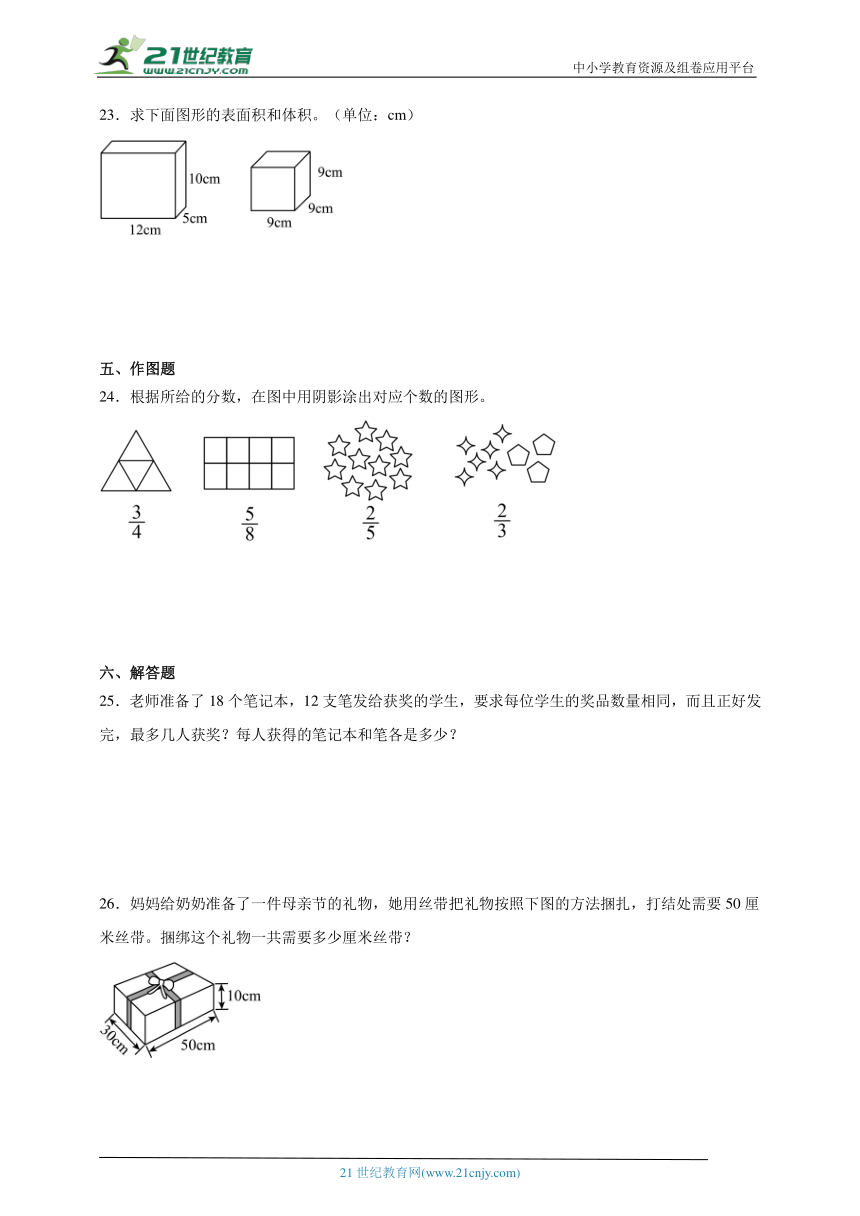
23.求下面图形的表面积和体积。(单位:cm)
五、作图题
24.根据所给的分数,在图中用阴影涂出对应个数的图形。
六、解答题
25.老师准备了18个笔记本,12支笔发给获奖的学生,要求每位学生的奖品数量相同,而且正好发完,最多几人获奖?每人获得的笔记本和笔各是多少?
26.妈妈给奶奶准备了一件母亲节的礼物,她用丝带把礼物按照下图的方法捆扎,打结处需要50厘米丝带。捆绑这个礼物一共需要多少厘米丝带?
27.把一张长36厘米,宽24厘米的长方形纸裁成同样大小,面积尽可能大的正方形,纸没有剩余,裁成的正方形的边长是多少厘米?
28.五3班学生排队做操,其中女生有26人,男生有39人,如果男生和女生分别站成每列人数相等的队列,那么每列最多站多少人?
29.一个正方体的容器,棱长12厘米,装满水后,倒入一底面长20厘米,宽15厘米,高18厘米的长方体容器中,现在水的深度是多少厘米?
30.一个从里面量长15厘米,宽10厘米的长方体容器,里面盛有9厘米高的水,把一个苹果放入水中淹没,水面上升了2厘米。这个苹果的体积是多少?
31.在学校里建一个游泳池,是不是你所向往的?希望长大的你能来为母校设计一个标准的游泳池!你知道吗?国际标准的长方体游泳池,它的长是50米,宽是25米,深是2.5米。请你先解决以下问题:
(1)这个游泳池占地多少平方米?
(2)平时注水时,水面距池口0.5米,按此计算,每换一次水需要注水多少立方米?
32.一个容器内装满了水。将大、中、小三个铁球这样操作:第一次,沉入小球;第二次,取出小球,沉入中球;第三次,取出中球,沉入大球。已知第一次溢出的水量是第二次的2倍,第三次溢出的水量是第一次的3倍。中球体积是大球体积的几分之几?
参考答案
1.B
【分析】根据题意,求这个游泳池的占地面积,与游泳池的深度和其它面都没有关系,只与游泳池的上面有关,根据长方形的面积公式:s=ab,把数据代入公式解答。
【详解】25×15=375(平方米)
答:这个游泳池的占地面积是375平方米。
故答案为:B
【点睛】此题主要考查长方形的面积公式和实际应用能力。
2.A
【分析】根据题意可知,参加科技小制作比赛的人数是8和6的公倍数,据此解答即可。
【详解】8=2×2×2;
6=2×3;
8和6的最小公倍数是2×2×2×3=24;
故答案为:A。
【点睛】因为6是3的倍数,所以只需要求8和6的公倍数即可。
3.A
【分析】一个数的最小倍数就是这个数的1倍,这个数乘1等于这个数本身。
【详解】根据分析可知,一个数的最小倍数一定等于它本身。
故答案为:A
【点睛】解答此题的关键是了解一个数的最小倍数是1倍。
4.B
【详解】解:一罐可口可乐的容量是355毫升; 故选B.
【分析】根据生活经验,对容积单位和数据的大小认识,可知计量一罐可口可乐的容量用“毫升”做单位;据此得解.
5.A
【分析】假设出原来长方体的长、宽、高,根据“长方体的体积=长×宽×高”表示出原来和现在长方体的体积,最后用除法求出长方体的体积扩大的倍数,据此解答。
【详解】假设原来长方体的长为a,宽为b,高为h,则现在长方体的长为3a,宽为3b,高为3h。
(3a×3b×3h)÷(a×b×h)
= 27abh÷abh
= 27
所以,一个长方体的长、宽高都扩大到原来的3倍,它的体积就扩大到原来的27倍。
故答案为:A
【点睛】掌握长方体的体积计算公式是解答题目的关键。
6.B
【分析】各个数位上数字之和是3的倍数,这个数就是3的倍数;由此根据3的倍数特征判断这个数即可。
【详解】一个两位数是3的倍数,要使这个两位数最大,十位上和个位上都可以是9,而99正好是3的倍数。
故选择:B
【点睛】此题主要考查学生对3的倍数特征的理解与认识。
7. 分子 分母 分数线 分数值
【分析】根据分数与除法的关系,直接填空即可。
【详解】(b≠0),所以被除数相当于分数的分子,除数相当于分数的分母,除号相当于分数线,商相当于分数值。
【点睛】考查了分数与除法的关系。
8. 2、0、54 9、13、19、87、1、201、3 2、13、19、3 9、87、201、54
【分析】本题需要明确奇数、质数、合数的概念,然后根据这些概念对给定的数字进行分类。偶数是能被2整除的数;奇数是不能被2整除的数;质数是一个大于1的自然数,除了1和它自身外,不能被其它自然数整除的数;合数是指自然数中除了能被1和本身整除外,还能被其它数(0除外)整除的数。
【详解】偶数:2、0、54;
奇数:9、13、19、87、1、201、3;
质数:2、13、19、3;
合数:9、87、201、54。
9. × × √
【分析】将每组分数的异分母转化为同分母分数,再确定两个分数是否相等。
【详解】,则,即和不相等,为×;
,则,即和不相等,为×;
,则,即和相等,为√。
10. 56 24
【分析】根据题意可知,三个正方体拼成一个长方体,长方体的长等于正方体棱长×3,长方体的宽等于正方体棱长,长方体的高等于正方体棱长;根据长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高,代入数据,即可解答。
【详解】拼成的长方体的长:2×3=6(cm),宽是2cm,高是2cm。
(6×2+6×2+2×2)×2
=(12+12+4)×2
=(24+4)×2
=28×2
=56(cm2)
6×2×2
=12×2
=24(cm3)
用三个棱长都是2cm的正方体拼成一个长方体,这个长方体的表面积是56cm2,体积是24cm3。
11.
4
16
64
【分析】正方体的棱长和、表面积、体积与棱长的关系分别为:棱长和=棱长×12,正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长。当棱长变为原来的4倍时,可以设原来正方体棱长为a,扩大4倍后,棱长为4a,再根据公式求出之前的棱长和,表面积和体积以及扩大4倍后的棱长和、表面积和体积,再用扩大后的除以扩大前的即可求解。
【详解】设原棱长为a,则新棱长为4a。
4a×12÷12a
=48a÷12a
=4
4a×4a×6÷
=÷
=16
4a×4a×4a÷
=÷
=64
一个正方体的棱长变为原来的4倍,则它的棱长和变为原来的4倍,表面积变为原来的16倍,体积变为原来的64倍。
12.
15块同样的蛋糕
5
1
3
【分析】根据题意,把整体平均分为若干份,这样的一份或几份都可以用分数来表示。盒子里面有15块同样的蛋糕,青青吃了,分数对应的整体是蛋糕总数。分母5表示平均分成的份数,分子1表示吃的份数,用15除以5,就是1份的块数。
【详解】根据分析可知:
15÷5=3(块)
盒子里面有15块同样的蛋糕,青青吃了,这里把15块同样的蛋糕看作单位“1”,把它平均分成5份,青青吃了1份,共吃了3块。
13. 6 8
【分析】根据从上面看到的图形可知,这个几何体的下层有4块正方体积木;根据从正面和左面看到的图形可知,这个几何体有2层,上层至少有2块正方体积木,最多有4块正方体积木;据此得出这个几何体最少和最多需要正方体积木的块数。
【详解】结合从正面、上面和左面看到的图形,可以得出下面的几何体:
(最少的搭法不唯一)
搭这样的几何体,最少需要6块正方体积木,最多需要8块正方体积木。
【点睛】本题考查根据三视图还原立体图形的能力,培养学生的空间想象力。
14.
【分析】这个分数的分子、分母均为11的倍数。11的倍数的特征是一个数从个位起向左,奇数位的数字之和减去偶数位的数字的差如果是0或者11的倍数,这个数就是11的倍数。这个分数的分子是154,1+4﹣5=0,分母是253,3+2﹣5=0。分子、分母中间的5划去,就相当于分子、分母都除以11,154÷11=14,253÷11=23,根据分数的基本性质,当然这两个分数相等了。这样的分数还很多,如的分子、分母划去中间的6是,也就相当于的分子、分母都除以11。据此解答。
【详解】的分子、分母都是11的倍数,把这个分数用11约分是,=;
类似这样的分数还很多,如的中间的两个6划去得,这两个分数相等;
【点睛】这个分数的分子、分母均为11的倍数,用11约分即是后面的分数,不容易看出。
15.√
【分析】能被2整除的数是偶数,不能被2整除的数是奇数,据此分析。
【详解】一个自然数不是奇数就是偶数,0也是偶数,判断正确。
故答案为:√
【点睛】此题考查自然数以及奇数偶数的判断方法。
16.×
【分析】3的倍数既有奇数,如9,又有偶数,如6。
【详解】6是3的倍数,6是偶数。
故答案为:×
【点睛】本题考查了3的倍数特征和奇数、偶数,不是2的倍数的数是奇数,是2的倍数的数是偶数。
17.×
【详解】判断一个数是不是2的倍数,要看这个数的个位上的数。个位上是0、2、4、6、8的数都是2的倍数,而不应该看十位上的数。
故答案为:×
18.×
【分析】从不同的位置观察物体,所看到的形状有可能完全相同,也有可能不同,据此判断即可。
【详解】从不同的位置观察物体,所看到的形状可能是不同的。
例如,观察下面的几何体,从正面看,看到的是由两个正方形拼成的长方形,从左面看,看到的是一个正方形。
故答案为:×
【点睛】此题主要考查从不同的位置观察物体,解题的关键是看能否举出例子,证明从不同的位置观察物体,所看到的形状可能是不同的。
19.×
【分析】根据互质数的意义,公因数只有1的两个数叫做互质数。19和35是互质数,也就是这两个数的公因数只有1。
【详解】如果两个数是互质数,那么它们的公因数就只有1。
19和35是互质数,也就是这两个数的公因数只有1,而不是没有公因数。
故答案为:×
20.×
【详解】略
21.
;;12;;15;
6;;1;;;1000
【详解】略
22.(1);(2)0
(3)1;(4)
【分析】(1)根据加法交换律a+b=b+a,加法结合律(a+b)+c=a+(b+c)把变成进行简算;
(2)先交换“”和“”的位置,再根据减法的性质a-b-c=a-(b+c)把变成进行简算;
(3)根据减法的性质a-b-c=a-(b+c)把变成进行简算;
(4)先算括号里面的减法,再算括号外面的加法。
【详解】(1)
(2)
(3)
(4)
23.(1)460平方厘米;600立方厘米
(2)486平方厘米;729立方厘米
【分析】根据,;正方体表面积=棱长×棱长×6,正方体体积=棱长×棱长×棱长,代入数据,列式计算即可。
【详解】根据分析可知:
(1)(12×5+10×5+12×10)×2
=(60+50+120)×2
=230×2
=460(平方厘米)
12×10×5
=120×5
=600(立方米)
长方体的表面积是460平方厘米,长方体的体积是600立方厘米。
(2)9×9×6
=81×6
=486(平方厘米)
9×9×9
=81×9
=729(立方厘米)
正方体的表面积是486平方厘米,正方体的体积是729立方厘米。
24.见详解
【分析】分数的意义为:将单位“1”平均分成若干份,表示这样一份或几份的数为分数。据此结合题目中的图形及分数进行涂色即可。
【详解】图一,此三角形被平均分成4份,则其中的3份为它的;
图二,此长方形被平均分成8份,则其中的5份为它的;
图三,共有10个五角星,将它们平均分成5份,则其中的是4个;
图四,共有图形9个,其中四角星6个,五边形3个,则四角形占所有图形的6÷9=。
如图:
25.6人;3个;2支
【分析】要求每位学生的奖品数量相同,而且正好发完,说明获奖的人数是18和12的公因数,求最多几人获奖,则是求18和12的最大公因数,再用18除以最大公因数的商,求出每人获得的笔记本是多少个,用12除以最大公因数的商,求出每人获得的笔是多少支,列式解答即可得到答案。
【详解】18=2×3×3
12=2×2×3
18和12的最大公因数是2×3=6。
所以最多6人获奖。
18÷6=3(个)
12÷6=2(支)
答:最多6人获奖,每人获得的笔记本是3个,笔是2支。
【点睛】此题的解题关键是运用求两个数的最大公因数的方法解决实际的问题。
26.250厘米
【分析】观察图形可知,丝带的长度=两条长的长度+两条宽的长度+四条高的长度+打结处的长度,据此进行计算即可。
【详解】50×2+30×2+10×4+50
=100+60+40+50
=160+40+50
=200+50
=250(厘米)
答:捆绑这个礼物一共需要250厘米丝带。
27.12厘米
【分析】根据题意,裁成的正方形边长最大是多少,是求36和24的最大公因数,根据求两个数的最大公因数的方法,即可得解。
【详解】36=2×2×3×3
24=2×2×2×3
36和24的最大公因数是:2×2×3=12。
所以正方形的边长最长是12厘米。
答:裁成的正方形的边长是12厘米。
【点睛】此题主要考查求两个数的最大公因数,能够根据求最大公因数的方法解决有关的实际问题。
28.13人
【分析】要使男生和女生分别站成每列人数相等的队列,那么每列的人数是26和39的公因数;求每列最多的人数,就是求26和39的最大公因数,据此解答即可。
【详解】26=2×13
39=3×13
26和39的最大公因数是13。
答:每列最多站13人。
【点睛】本题考查求两个数的最大公因数的方法解决实际问题。
29.5.76厘米
【详解】试题分析:先根据正方体的体积公式求出水的体积是:12×12×12=1728立方厘米,倒入长方体容器后,水的体积不变,用水的体积除以长方体容器的底面积,就是水的高度.
解:12×12×12÷(20×15),
=1728÷300,
=5.76(厘米);
答:现在水的深度是5.76厘米.
点评:此题考查了正方体和长方体的体积公式的综合应用.
30.300立方厘米
【分析】根据题意,把一个苹果浸没在有水的长方体容器中,水面上升了2厘米,那么水上升部分的体积等于苹果的体积,根据长方体的体积=长×宽×高,代入数据计算求解。
【详解】15×10×2
=150×2
=300(立方厘米)
答:这个苹果的体积是300立方厘米。
31.
(1)1250平方米
(2)2500立方米
【分析】(1)根据题意,已知它的长是50米,宽是25米,游泳池的占地面积即其底面积,用长乘宽计算,列式计算即可。
(2)水的深度就是游泳池的深度减去水面距池口的距离,再根据,列式计算得到水的体积。
【详解】根据分析可知:
(1)50×25=1250(平方米)
答:这个游泳池占地1250平方米。
(2)水深: 2.5-0.5=2(米)
注水体积:
50×25×2
=1250×2
=2500(立方米)
答:每换一次水需要注水2500立方米。
32.
【分析】第一次,沉入小球,溢出的水量是小球的体积;第二次,取出小球,沉入中球,溢出的水量=中球体积-小球体积;第三次,取出中球,沉入大球,溢出的水量=大球体积-中球体积。第一次溢出的水量是第二次的2倍,假设小球体积是2,则中球体积-小球体积是1,那么中球体积是3。第三次溢出的水量是第一次的3倍,即大球体积-中球体积=小球体积×3,由此确定大球体积,将大球体积看作单位“1”,中球体积÷大球体积=中球体积是大球体积的几分之几。
【详解】假设小球体积是2,则中球体积是3。
大球体积-中球体积=2×3=6
大球体积=3+6=9
3÷9=
答:中球体积是大球体积的。
【点睛】关键是根据溢出的水量,确定小球、中球和大球体积之间的关系。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
(期末冲刺)2024-2025学年五年级数学下册常考易错提升试卷(人教版)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.一个长方体游泳池,长25米,宽15米,深1.5米,这个游泳池占地( )平方米。
A.750 B.375 C.27
2.实验小学的学生们参加科技小制作比赛,其中有的人获得一等奖,有的人获得二等奖,有的人获得三等奖,其余的人获得优秀奖,该校可能有( )人参加科技小制作比赛。
A.24 B.30 C.36 D.50
3.一个数的最小倍数一定( )它本身。
A.等于 B.大于 C.小于
4.一罐可口可乐的容量是( )
A.355米3 B.355毫升 C.355分米3
5.一个长方体的长、宽、高都扩大到原来的3倍,它的体积扩大到原来的( )。
A.27倍 B.9倍 C.3倍
6.一个两位数是3的倍数,这个两位数最大可能是( )。
A.90 B.99 C.98 D.100
二、填空题
7.被除数相当于分数的( ),除数相当于分数的( ),除号相当于( ),商相当于( )。
8.在2、9、13、19、87、1、201、3、0、54中,偶数有( ),奇数有( ),质数有( ),合数有( )。
9.下面每组中的两个分数是否相等?相等的画“√”,不相等的画“×”。
和( ) 和( ) 和( )
10.用三个棱长都是2cm的正方体拼成一个长方体,这个长方体的表面积是( )cm2,体积是( )cm3。
11.一个正方体的棱长变为原来的4倍,则它的棱长和变为原来的( )倍,表面积变为原来的( )倍,体积变为原来的( )倍。
12.盒子里面有15块同样的蛋糕,青青吃了,这里把( )看作单位“1”,把它平均分成( )份,青青吃了( )份,共吃了( )块。
13.用同样的正方体积木搭几何体,要求从正面、上面和左面看到的图形都是,搭这样的几何体,最少需要( )块正方体积木,最多需要( )块。
14.有一个学生无意间将中间的两个5划去得,他惊讶地发现这两个分数居然相等。这是偶然的吗?他进行了研究,发现这样的分数还有很多,请你也写出一个类似这样的分数 。
三、判断题
15.一个自然数不是奇数就是偶数。( )
16.3的倍数都是奇数。( )
17.一个两位数,十位上是8,它一定是2的倍数。 ( )
18.从不同的位置观察物体,所看到的形状完全相同。( )
19.因为19和35是互质数,所以19和35没有公因数。 。
20.所有的质数加上1后,就变成了合数. ( )
四、计算题
21.直接写出得数。
+= -= 7.2÷0.6= 1-= 1.5×7+1.5×3= +=
7.5×0.8= += += -= ++= 103=
22.计算下面各题,能简算的要简算。
(1) (2)
(3) (4)
23.求下面图形的表面积和体积。(单位:cm)
五、作图题
24.根据所给的分数,在图中用阴影涂出对应个数的图形。
六、解答题
25.老师准备了18个笔记本,12支笔发给获奖的学生,要求每位学生的奖品数量相同,而且正好发完,最多几人获奖?每人获得的笔记本和笔各是多少?
26.妈妈给奶奶准备了一件母亲节的礼物,她用丝带把礼物按照下图的方法捆扎,打结处需要50厘米丝带。捆绑这个礼物一共需要多少厘米丝带?
27.把一张长36厘米,宽24厘米的长方形纸裁成同样大小,面积尽可能大的正方形,纸没有剩余,裁成的正方形的边长是多少厘米?
28.五3班学生排队做操,其中女生有26人,男生有39人,如果男生和女生分别站成每列人数相等的队列,那么每列最多站多少人?
29.一个正方体的容器,棱长12厘米,装满水后,倒入一底面长20厘米,宽15厘米,高18厘米的长方体容器中,现在水的深度是多少厘米?
30.一个从里面量长15厘米,宽10厘米的长方体容器,里面盛有9厘米高的水,把一个苹果放入水中淹没,水面上升了2厘米。这个苹果的体积是多少?
31.在学校里建一个游泳池,是不是你所向往的?希望长大的你能来为母校设计一个标准的游泳池!你知道吗?国际标准的长方体游泳池,它的长是50米,宽是25米,深是2.5米。请你先解决以下问题:
(1)这个游泳池占地多少平方米?
(2)平时注水时,水面距池口0.5米,按此计算,每换一次水需要注水多少立方米?
32.一个容器内装满了水。将大、中、小三个铁球这样操作:第一次,沉入小球;第二次,取出小球,沉入中球;第三次,取出中球,沉入大球。已知第一次溢出的水量是第二次的2倍,第三次溢出的水量是第一次的3倍。中球体积是大球体积的几分之几?
参考答案
1.B
【分析】根据题意,求这个游泳池的占地面积,与游泳池的深度和其它面都没有关系,只与游泳池的上面有关,根据长方形的面积公式:s=ab,把数据代入公式解答。
【详解】25×15=375(平方米)
答:这个游泳池的占地面积是375平方米。
故答案为:B
【点睛】此题主要考查长方形的面积公式和实际应用能力。
2.A
【分析】根据题意可知,参加科技小制作比赛的人数是8和6的公倍数,据此解答即可。
【详解】8=2×2×2;
6=2×3;
8和6的最小公倍数是2×2×2×3=24;
故答案为:A。
【点睛】因为6是3的倍数,所以只需要求8和6的公倍数即可。
3.A
【分析】一个数的最小倍数就是这个数的1倍,这个数乘1等于这个数本身。
【详解】根据分析可知,一个数的最小倍数一定等于它本身。
故答案为:A
【点睛】解答此题的关键是了解一个数的最小倍数是1倍。
4.B
【详解】解:一罐可口可乐的容量是355毫升; 故选B.
【分析】根据生活经验,对容积单位和数据的大小认识,可知计量一罐可口可乐的容量用“毫升”做单位;据此得解.
5.A
【分析】假设出原来长方体的长、宽、高,根据“长方体的体积=长×宽×高”表示出原来和现在长方体的体积,最后用除法求出长方体的体积扩大的倍数,据此解答。
【详解】假设原来长方体的长为a,宽为b,高为h,则现在长方体的长为3a,宽为3b,高为3h。
(3a×3b×3h)÷(a×b×h)
= 27abh÷abh
= 27
所以,一个长方体的长、宽高都扩大到原来的3倍,它的体积就扩大到原来的27倍。
故答案为:A
【点睛】掌握长方体的体积计算公式是解答题目的关键。
6.B
【分析】各个数位上数字之和是3的倍数,这个数就是3的倍数;由此根据3的倍数特征判断这个数即可。
【详解】一个两位数是3的倍数,要使这个两位数最大,十位上和个位上都可以是9,而99正好是3的倍数。
故选择:B
【点睛】此题主要考查学生对3的倍数特征的理解与认识。
7. 分子 分母 分数线 分数值
【分析】根据分数与除法的关系,直接填空即可。
【详解】(b≠0),所以被除数相当于分数的分子,除数相当于分数的分母,除号相当于分数线,商相当于分数值。
【点睛】考查了分数与除法的关系。
8. 2、0、54 9、13、19、87、1、201、3 2、13、19、3 9、87、201、54
【分析】本题需要明确奇数、质数、合数的概念,然后根据这些概念对给定的数字进行分类。偶数是能被2整除的数;奇数是不能被2整除的数;质数是一个大于1的自然数,除了1和它自身外,不能被其它自然数整除的数;合数是指自然数中除了能被1和本身整除外,还能被其它数(0除外)整除的数。
【详解】偶数:2、0、54;
奇数:9、13、19、87、1、201、3;
质数:2、13、19、3;
合数:9、87、201、54。
9. × × √
【分析】将每组分数的异分母转化为同分母分数,再确定两个分数是否相等。
【详解】,则,即和不相等,为×;
,则,即和不相等,为×;
,则,即和相等,为√。
10. 56 24
【分析】根据题意可知,三个正方体拼成一个长方体,长方体的长等于正方体棱长×3,长方体的宽等于正方体棱长,长方体的高等于正方体棱长;根据长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高,代入数据,即可解答。
【详解】拼成的长方体的长:2×3=6(cm),宽是2cm,高是2cm。
(6×2+6×2+2×2)×2
=(12+12+4)×2
=(24+4)×2
=28×2
=56(cm2)
6×2×2
=12×2
=24(cm3)
用三个棱长都是2cm的正方体拼成一个长方体,这个长方体的表面积是56cm2,体积是24cm3。
11.
4
16
64
【分析】正方体的棱长和、表面积、体积与棱长的关系分别为:棱长和=棱长×12,正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长。当棱长变为原来的4倍时,可以设原来正方体棱长为a,扩大4倍后,棱长为4a,再根据公式求出之前的棱长和,表面积和体积以及扩大4倍后的棱长和、表面积和体积,再用扩大后的除以扩大前的即可求解。
【详解】设原棱长为a,则新棱长为4a。
4a×12÷12a
=48a÷12a
=4
4a×4a×6÷
=÷
=16
4a×4a×4a÷
=÷
=64
一个正方体的棱长变为原来的4倍,则它的棱长和变为原来的4倍,表面积变为原来的16倍,体积变为原来的64倍。
12.
15块同样的蛋糕
5
1
3
【分析】根据题意,把整体平均分为若干份,这样的一份或几份都可以用分数来表示。盒子里面有15块同样的蛋糕,青青吃了,分数对应的整体是蛋糕总数。分母5表示平均分成的份数,分子1表示吃的份数,用15除以5,就是1份的块数。
【详解】根据分析可知:
15÷5=3(块)
盒子里面有15块同样的蛋糕,青青吃了,这里把15块同样的蛋糕看作单位“1”,把它平均分成5份,青青吃了1份,共吃了3块。
13. 6 8
【分析】根据从上面看到的图形可知,这个几何体的下层有4块正方体积木;根据从正面和左面看到的图形可知,这个几何体有2层,上层至少有2块正方体积木,最多有4块正方体积木;据此得出这个几何体最少和最多需要正方体积木的块数。
【详解】结合从正面、上面和左面看到的图形,可以得出下面的几何体:
(最少的搭法不唯一)
搭这样的几何体,最少需要6块正方体积木,最多需要8块正方体积木。
【点睛】本题考查根据三视图还原立体图形的能力,培养学生的空间想象力。
14.
【分析】这个分数的分子、分母均为11的倍数。11的倍数的特征是一个数从个位起向左,奇数位的数字之和减去偶数位的数字的差如果是0或者11的倍数,这个数就是11的倍数。这个分数的分子是154,1+4﹣5=0,分母是253,3+2﹣5=0。分子、分母中间的5划去,就相当于分子、分母都除以11,154÷11=14,253÷11=23,根据分数的基本性质,当然这两个分数相等了。这样的分数还很多,如的分子、分母划去中间的6是,也就相当于的分子、分母都除以11。据此解答。
【详解】的分子、分母都是11的倍数,把这个分数用11约分是,=;
类似这样的分数还很多,如的中间的两个6划去得,这两个分数相等;
【点睛】这个分数的分子、分母均为11的倍数,用11约分即是后面的分数,不容易看出。
15.√
【分析】能被2整除的数是偶数,不能被2整除的数是奇数,据此分析。
【详解】一个自然数不是奇数就是偶数,0也是偶数,判断正确。
故答案为:√
【点睛】此题考查自然数以及奇数偶数的判断方法。
16.×
【分析】3的倍数既有奇数,如9,又有偶数,如6。
【详解】6是3的倍数,6是偶数。
故答案为:×
【点睛】本题考查了3的倍数特征和奇数、偶数,不是2的倍数的数是奇数,是2的倍数的数是偶数。
17.×
【详解】判断一个数是不是2的倍数,要看这个数的个位上的数。个位上是0、2、4、6、8的数都是2的倍数,而不应该看十位上的数。
故答案为:×
18.×
【分析】从不同的位置观察物体,所看到的形状有可能完全相同,也有可能不同,据此判断即可。
【详解】从不同的位置观察物体,所看到的形状可能是不同的。
例如,观察下面的几何体,从正面看,看到的是由两个正方形拼成的长方形,从左面看,看到的是一个正方形。
故答案为:×
【点睛】此题主要考查从不同的位置观察物体,解题的关键是看能否举出例子,证明从不同的位置观察物体,所看到的形状可能是不同的。
19.×
【分析】根据互质数的意义,公因数只有1的两个数叫做互质数。19和35是互质数,也就是这两个数的公因数只有1。
【详解】如果两个数是互质数,那么它们的公因数就只有1。
19和35是互质数,也就是这两个数的公因数只有1,而不是没有公因数。
故答案为:×
20.×
【详解】略
21.
;;12;;15;
6;;1;;;1000
【详解】略
22.(1);(2)0
(3)1;(4)
【分析】(1)根据加法交换律a+b=b+a,加法结合律(a+b)+c=a+(b+c)把变成进行简算;
(2)先交换“”和“”的位置,再根据减法的性质a-b-c=a-(b+c)把变成进行简算;
(3)根据减法的性质a-b-c=a-(b+c)把变成进行简算;
(4)先算括号里面的减法,再算括号外面的加法。
【详解】(1)
(2)
(3)
(4)
23.(1)460平方厘米;600立方厘米
(2)486平方厘米;729立方厘米
【分析】根据,;正方体表面积=棱长×棱长×6,正方体体积=棱长×棱长×棱长,代入数据,列式计算即可。
【详解】根据分析可知:
(1)(12×5+10×5+12×10)×2
=(60+50+120)×2
=230×2
=460(平方厘米)
12×10×5
=120×5
=600(立方米)
长方体的表面积是460平方厘米,长方体的体积是600立方厘米。
(2)9×9×6
=81×6
=486(平方厘米)
9×9×9
=81×9
=729(立方厘米)
正方体的表面积是486平方厘米,正方体的体积是729立方厘米。
24.见详解
【分析】分数的意义为:将单位“1”平均分成若干份,表示这样一份或几份的数为分数。据此结合题目中的图形及分数进行涂色即可。
【详解】图一,此三角形被平均分成4份,则其中的3份为它的;
图二,此长方形被平均分成8份,则其中的5份为它的;
图三,共有10个五角星,将它们平均分成5份,则其中的是4个;
图四,共有图形9个,其中四角星6个,五边形3个,则四角形占所有图形的6÷9=。
如图:
25.6人;3个;2支
【分析】要求每位学生的奖品数量相同,而且正好发完,说明获奖的人数是18和12的公因数,求最多几人获奖,则是求18和12的最大公因数,再用18除以最大公因数的商,求出每人获得的笔记本是多少个,用12除以最大公因数的商,求出每人获得的笔是多少支,列式解答即可得到答案。
【详解】18=2×3×3
12=2×2×3
18和12的最大公因数是2×3=6。
所以最多6人获奖。
18÷6=3(个)
12÷6=2(支)
答:最多6人获奖,每人获得的笔记本是3个,笔是2支。
【点睛】此题的解题关键是运用求两个数的最大公因数的方法解决实际的问题。
26.250厘米
【分析】观察图形可知,丝带的长度=两条长的长度+两条宽的长度+四条高的长度+打结处的长度,据此进行计算即可。
【详解】50×2+30×2+10×4+50
=100+60+40+50
=160+40+50
=200+50
=250(厘米)
答:捆绑这个礼物一共需要250厘米丝带。
27.12厘米
【分析】根据题意,裁成的正方形边长最大是多少,是求36和24的最大公因数,根据求两个数的最大公因数的方法,即可得解。
【详解】36=2×2×3×3
24=2×2×2×3
36和24的最大公因数是:2×2×3=12。
所以正方形的边长最长是12厘米。
答:裁成的正方形的边长是12厘米。
【点睛】此题主要考查求两个数的最大公因数,能够根据求最大公因数的方法解决有关的实际问题。
28.13人
【分析】要使男生和女生分别站成每列人数相等的队列,那么每列的人数是26和39的公因数;求每列最多的人数,就是求26和39的最大公因数,据此解答即可。
【详解】26=2×13
39=3×13
26和39的最大公因数是13。
答:每列最多站13人。
【点睛】本题考查求两个数的最大公因数的方法解决实际问题。
29.5.76厘米
【详解】试题分析:先根据正方体的体积公式求出水的体积是:12×12×12=1728立方厘米,倒入长方体容器后,水的体积不变,用水的体积除以长方体容器的底面积,就是水的高度.
解:12×12×12÷(20×15),
=1728÷300,
=5.76(厘米);
答:现在水的深度是5.76厘米.
点评:此题考查了正方体和长方体的体积公式的综合应用.
30.300立方厘米
【分析】根据题意,把一个苹果浸没在有水的长方体容器中,水面上升了2厘米,那么水上升部分的体积等于苹果的体积,根据长方体的体积=长×宽×高,代入数据计算求解。
【详解】15×10×2
=150×2
=300(立方厘米)
答:这个苹果的体积是300立方厘米。
31.
(1)1250平方米
(2)2500立方米
【分析】(1)根据题意,已知它的长是50米,宽是25米,游泳池的占地面积即其底面积,用长乘宽计算,列式计算即可。
(2)水的深度就是游泳池的深度减去水面距池口的距离,再根据,列式计算得到水的体积。
【详解】根据分析可知:
(1)50×25=1250(平方米)
答:这个游泳池占地1250平方米。
(2)水深: 2.5-0.5=2(米)
注水体积:
50×25×2
=1250×2
=2500(立方米)
答:每换一次水需要注水2500立方米。
32.
【分析】第一次,沉入小球,溢出的水量是小球的体积;第二次,取出小球,沉入中球,溢出的水量=中球体积-小球体积;第三次,取出中球,沉入大球,溢出的水量=大球体积-中球体积。第一次溢出的水量是第二次的2倍,假设小球体积是2,则中球体积-小球体积是1,那么中球体积是3。第三次溢出的水量是第一次的3倍,即大球体积-中球体积=小球体积×3,由此确定大球体积,将大球体积看作单位“1”,中球体积÷大球体积=中球体积是大球体积的几分之几。
【详解】假设小球体积是2,则中球体积是3。
大球体积-中球体积=2×3=6
大球体积=3+6=9
3÷9=
答:中球体积是大球体积的。
【点睛】关键是根据溢出的水量,确定小球、中球和大球体积之间的关系。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
