2.2《立方根》小节复习题 (含详解)苏科版八年级数学上册
文档属性
| 名称 | 2.2《立方根》小节复习题 (含详解)苏科版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 817.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-04 00:00:00 | ||
图片预览



文档简介
2.2《立方根》小节复习题
题型01 立方根的概念理解
1.下列说法正确的是( )
A.任何数的立方根都只有一个 B.如果一个数有立方根,那么这个数一定有平方根
C.一个数的立方根比这个数的平方根小 D.一个数的立方根有两个,它们互为相反数
2.下列没有意义的是( )
A. B. C. D.
3.一个自然数a的算术平方根为x,那么的立方根是( )
A. B. C. D.
4.下列说法正确的是( )
A.一个数的立方根有两个,它们互为相反数 B.负数没有立方根
C.一个数有立方根,那么它的立方根一定为正数 D.一个数的立方根与这个数同号
题型02 求一个数的立方根
1.-的立方根是 ,的立方根是 .
2.下列说法正确的是( )
A.的立方根是 B.的立方根是
C.立方根等于本身的数是和 D.
3.立方根和平方根都等于本身的数是 .
4.的立方根的平方根是 .
题型03 利用开立方解方程
1.求下列各式中x的值:
(1);(2).(3).
2.求下列各式中x的值:
(1);(2);(3)
3.解方程:(1); (2);(3)
4.解下列方程
(1) ( 2) (3).
题型04 立方根的性质
1.先阅读材料,再解答问题.
,,.
,,.
,,.,
, , .
(1)完成上面的填空,并猜测互为相反数的两个数的立方根的关系为 .
(2)计算的值.
2.下列计算,错误的是( )
A. B. C. D.
3.已知,则的值为
4.【发现】①;②;③;④;……
根据上述等式反映的规律,请再写出一个等式:___________.
【归纳】等式①,②,③,④所反映的规律,可归纳为一个真命题:
对于任意两个有理数,,若_____,则;反之也成立.
【应用】根据上述所归纳的真命题,解决下列问题:若与的值互为相反数,求的值.
题型05 立方根小数点位数移动规律
1.(1)填表:
a 0.001 1 1000 1000000
1 10
由表你发现了:被开方数的小数点向右(或左)移动 位,其立方根的小数点向右(或左)移动 位;
(2)根据你发现的规律填空:①已知,则 ;②已知,则 .
(3)用铁皮制作一个封闭的正方体,它的体积为立方米,需要多大面积的铁皮?
2.已知,,,,,则 , .
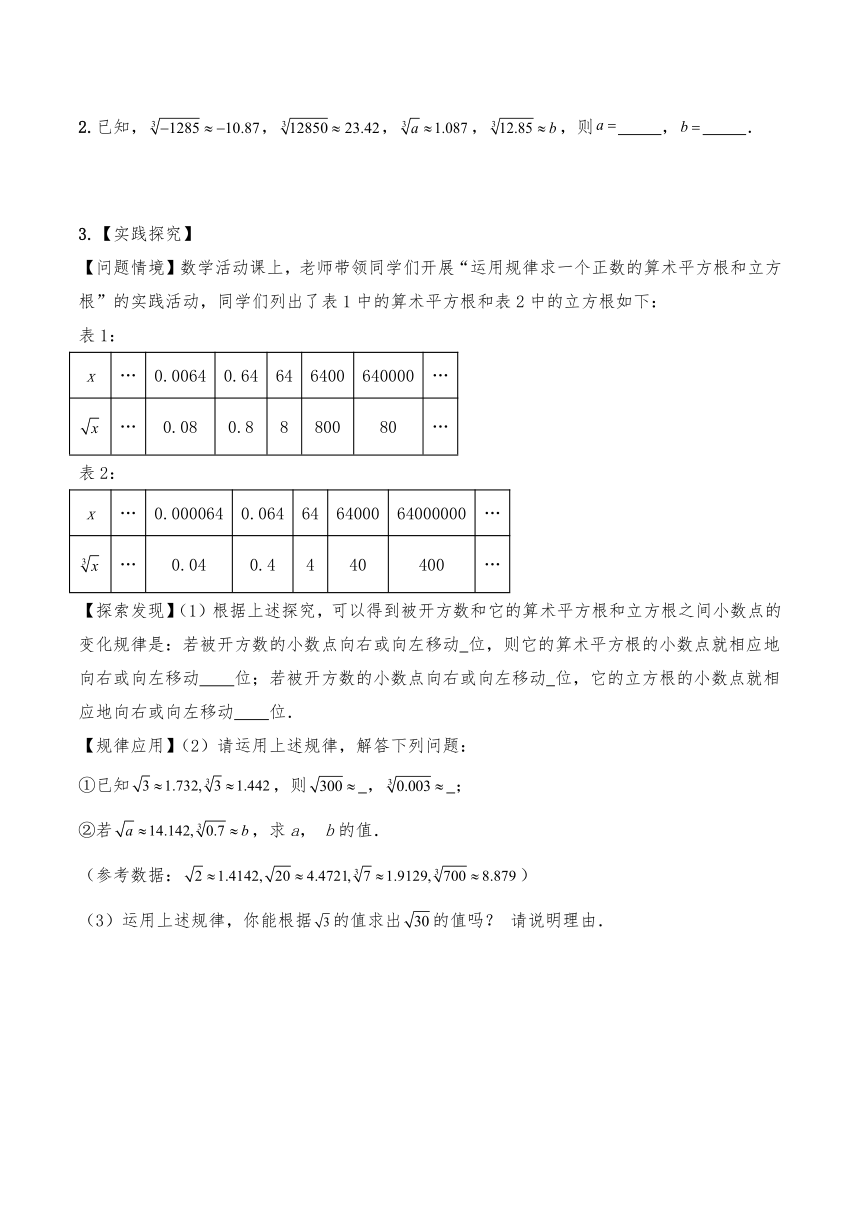
3.【实践探究】
【问题情境】数学活动课上,老师带领同学们开展“运用规律求一个正数的算术平方根和立方根”的实践活动,同学们列出了表1中的算术平方根和表2中的立方根如下:
表1:
x … 0.0064 0.64 64 6400 640000 …
… 0.08 0.8 8 800 80 …
表2:
x … 0.000064 0.064 64 64000 64000000 …
… 0.04 0.4 4 40 400 …
【探索发现】(1)根据上述探究,可以得到被开方数和它的算术平方根和立方根之间小数点的变化规律是:若被开方数的小数点向右或向左移动 位,则它的算术平方根的小数点就相应地向右或向左移动 位;若被开方数的小数点向右或向左移动 位,它的立方根的小数点就相应地向右或向左移动 位.
【规律应用】(2)请运用上述规律,解答下列问题:
①已知,则 , ;
②若,求a, b的值.
(参考数据:)
(3)运用上述规律,你能根据的值求出的值吗? 请说明理由.
题型06 立方根的实际应用
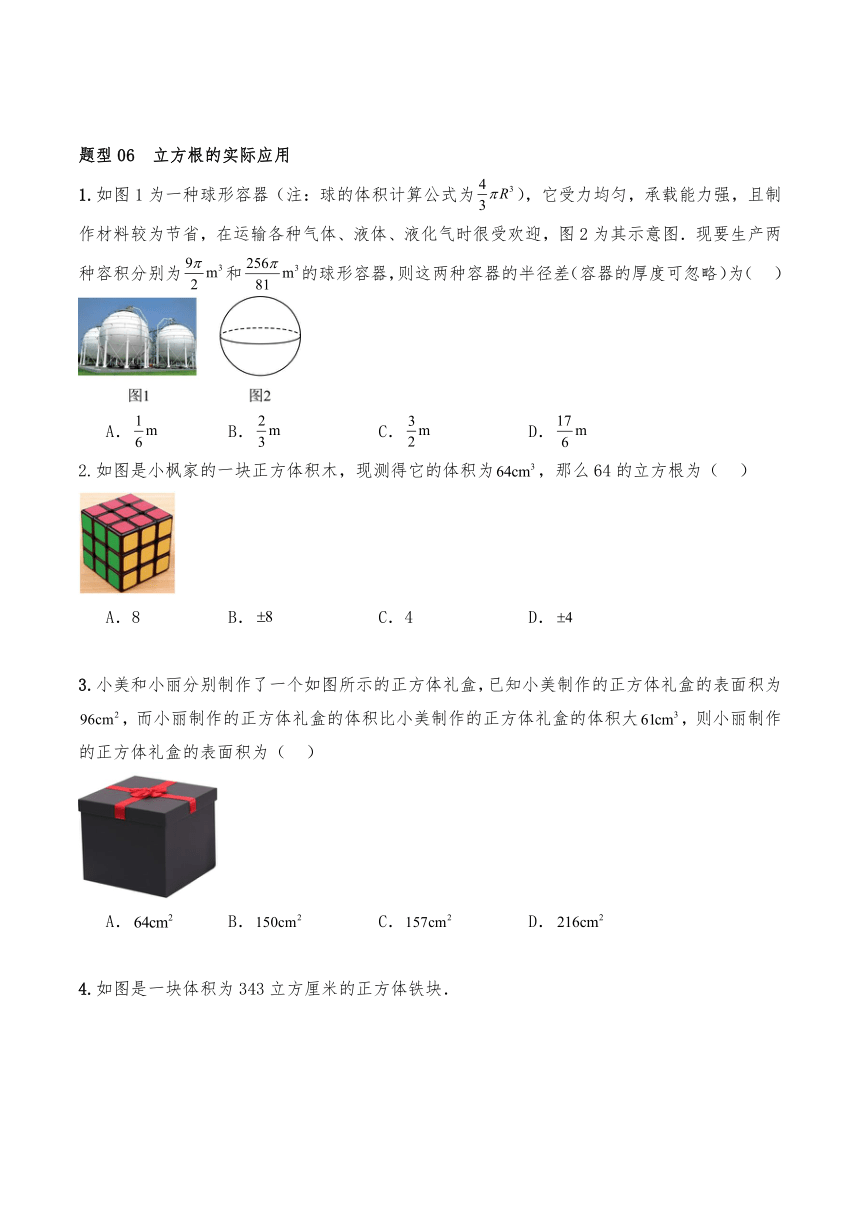
1.如图1为一种球形容器(注:球的体积计算公式为),它受力均匀,承载能力强,且制作材料较为节省,在运输各种气体、液体、液化气时很受欢迎,图2为其示意图.现要生产两种容积分别为和的球形容器,则这两种容器的半径差(容器的厚度可忽略)为( )
A. B. C. D.
2.如图是小枫家的一块正方体积木,现测得它的体积为,那么64的立方根为( )
A.8 B. C.4 D.
3.小美和小丽分别制作了一个如图所示的正方体礼盒,已知小美制作的正方体礼盒的表面积为,而小丽制作的正方体礼盒的体积比小美制作的正方体礼盒的体积大,则小丽制作的正方体礼盒的表面积为( )
A. B. C. D.
4.如图是一块体积为343立方厘米的正方体铁块.
(1)求该正方体铁块的棱长;(2)现在工厂要将这块铁块熔化,重新锻造成两个棱长为3厘米的小正方体铁块和一个底面为正方形的长方体铁块.若长方体铁块的高为1厘米,求长方体铁块的底面正方形的边长.
题型07 算术平方根与立方根的综合运用
1.已知的立方根是的算术平方根是.
(1)求、的值;(2)求的平方根.
2.已知的平方根是,的立方根为.
(1)求a与b的值;(2)求的算术平方根和立方根.
3.已知是的算术平方根,的立方根是.
(1)求,的值;(2)求的立方根.
4.已知的立方根是3,的算术平方根是4.
(1)求a,b的值;(2)求的平方根.
题型08 阅读材料与新定义问题考法
1.我们已经从定义、表示、特征三个方面研究了平方根与立方根.实际上,数的方根的概念可以推广.类比平方根与立方根的学习,博学小组合作探究了次方根,下面是他们写的“次方根的学习档案”的部分内容.请认真阅读,并帮助其补充完整.
次方根的学习档案
定义:如果一个数的次方等于(是大于1的整数),即,那么这个数就叫做的次方根. 例如2是16的 . 求一个数的次方根的运算叫做 ,叫做 . 特征:根据次方根的意义,结合平方根与立方根的特征,探究发现正数、0和负数的次方根的特征如下: 正数的次方根是正数;0的次方根是 ;负数 .
2.我国著名数学家华罗庚有一次在飞机上看到他的助手阅读的杂志上有一道智力题:一个数是,求它的立方根.华罗庚脱口而出:.华罗庚是按照下面的方法算出的:由,,从而确定是两位数,由的个位上的数是,所以能确定的个位上的数是,如果划去后面的三位得到数,而,,由此就能确定的十位上的数是,所以的立方根是.模仿华罗庚的方法,请确定的立方根是 .
3.若n为自然数,对下面判断正确的是( )
A.一定无意义 B.一定有意义
C.若n为奇数,则必有意义 D.一定成立
4.已知变换:例如则的变换结果是( )
A. B. C. D.
参考答案
题型01 立方根的概念理解
1.A
【详解】解:∵一个正数有一个正的立方根,一个负数有一个负的立方根,0的立方根是0,
∴A选项说法正确;D选项说法不正确.
∵一个负数有一个负的立方根,但负数没有平方根,∴B选项说法不正确;
一个数的立方根不一定比这个数的平方根小,例如0的平方根和立方根相等,∴C选项说法不正确;
综上,说法正确的是A选项,故选:A.
2.A
【详解】解:A、,负数没有算术平方根,没有意义,符合题意;
B、表示的算术平方根,有意义,不符合题意;
C、表示的立平方根,有意义,不符合题意;
D、表示的立平方根,有意义,不符合题意;故选:A.
3.C
【详解】解:∵一个自然数的算术平方根为,∴,∴,
∴的立方根是,故选:C.
4.D
【详解】A、一个数的立方根只有一个,错误;B、负数有立方根,错误;
C、一个数有立方根,那么它的立方根不一定为正数,错误;
D、一个数的立方根与这个数同号,正确.故选:D.
题型02 求一个数的立方根
1.
【详解】解:的平方根是=;
∵,∴的立方根为=;故答案为:;.
2.D
【详解】解:、的立方根是,原选项说法错误,不符合题意;
、,的立方根是.原选项说法错误,不符合题意;
、立方根等于本身的数是,和,原选项说法错误,不符合题意;
、,原选项说法正确,符合题意;故选:.
3.0
【详解】解:立方根等于它本身的数是0,,平方根等于它本身的数是0,
所以立方根和平方根都等于本身的数是0.故答案为:0.
4.
【详解】解:∵,8的立方根是2∴的立方根是2,
∴的立方根的平方根是故答案为:.
题型03 利用开立方解方程
1.(1)解:∵,
∴,
∴,
∴;
(2),
,
,
;
(3)解:,
整理得,
∴,
∴.
2.解:(1)
∴.
(2)解:,
∴,
∴,
解得:.
(3)解:,
,
,
.
3.(1)解:
(2)解:
或.
(3)解:∵,
∴,
∴,
4.(1)解:,
∴,
∴,
∴;
(2)解:,
∴,
∴.
(3)解:,
,
,
.
题型04 立方根的性质
1.(1)解:,,;
∴互为相反数的两个数的立方根互为相反数;
故答案为:;;; ,相反数
(2)解:
.
2.D
【详解】解:A.,故此选项不合题意; B.,故此选项不合题意;
C.,故此选项不合题意; D. ,故此选项符合题意. 故选:D.
3.或2或3
【详解】解:∵,∴,
∴或,∴或或;故答案为:或2或3.
4.解:发现:根据题意;如(答案不唯一);
故答案为:(答案不唯一)
归纳:根据等式①,②,③,④所反映的规律,可归纳为一个真命题:
对于任意两个有理数,,若,则;反之也成立;故答案为:;
应用:与的值互为相反数;
, 解得,则.
题型05 立方根小数点位数移动规律
1.(1)解:填表:
a 0.001 1 1000 1000000
1 10
规律:数的小数点每移动三位,它的立方根的小数点就向相同方向移动一位;
(2)解:①∵,∴;
②∵∴;
(3)解:设正方体的棱长为米,则,,
(平方米),答:需要大约平方米的铁皮.
2. 1.285 2.342
【详解】解:,
故答案为:1.285;2.342
3.解:(1)由表格可得,若被开方数的小数点向右或向左移动2位,则它的算术平方根的小数点就相应地向右或向左移动1位;若被开方数的小数点向右或向左移动3位,它的立方根的小数点就相应地向右或向左移动1位,故答案为:2,1;3,1;
(2)①∵,∴,,故答案为:17.32,0.1442;
②∵,,∴,,
∴,,故答案为:200,0.8879;
(3)∵,∴,,∴不能求出的值.
题型06 立方根的实际应用
1.A
【详解】解:设一种球形容器的半径为,则,解得:
另一种球形容器的半径为,则,解得:
则这两种容器的半径差为:,故选:A
2.C
【详解】∵,∴64的立方根是4.故选:C.
3.B
【详解】解:设小美正方体棱长为,,得,,
小美制作的正方体礼盒的棱长为:,其体积为:,
小丽制作的正方体礼盒的体积为:,则小丽制作的正方体礼盒的棱长为:,
小丽制作的正方体礼盒的表面积为:;故选:B.
4.(1)解:由题意得,该正方体铁块的棱长为(厘米),∴该正方体铁块的棱长为7厘米.
(2)解:由题意,长方体的体积为:(立方厘米),
∴长方体的底面面积为:(平分厘米),
∴长方体铁块的底面正方形的边长为:(厘米),
∴长方体铁块的底面正方形的边长为17厘米.
题型07 算术平方根与立方根的综合运用
1.(1)解:的立方根是,的算术平方根是,
,,;
(2)解:当时,
17的平方根是,的平方根是.
2.(1)解:的平方根是,,解得;
又的立方根为,,解得;,.
(2)由(1)可知:,
的算术平方根为,的立方根为.
3.(1)解:是的算术平方根,,解得:,
的立方根是,∴,即解得:;
(2),,,的立方根是.
4.(1)解:∵的立方根是3,的算术平方根是4,
∴,,解得:,,故a的值为5,b的值为.
(2)解:由题知,,∵,∴的平方根是.
题型08 阅读材料与新定义问题考法
1.解∶,2是16的四次方根;
如果一个数x的n(n是大于|的整数)次方等于a,即,那么这个数x就叫做a的n次方根,求一个数a的n次方根的运算叫做开n次方,a叫做被开方数,n叫做根指数;正数的n次方根是正的;0的n次方根是0;负数不存在偶次方根,奇次方根为负数,
故答案为:四次方根;开次方;被开方数;0;没有偶次方根,奇次方根为负数.
2.
【详解】解:,,是两位数,
又只有个位上是的数的立方的个位上的数是,的个位上的数是,
如果划去后面的三位得到,而,,
十位上的数是,的立方根是,故答案为:.
3.C
【详解】解:当为偶数,时,有意义,
当为偶数时,必有意义,不一定成立,故C正确,ABD错误.故选:C.
4.C
【详解】解:由题意得,,,,故选:C.
题型01 立方根的概念理解
1.下列说法正确的是( )
A.任何数的立方根都只有一个 B.如果一个数有立方根,那么这个数一定有平方根
C.一个数的立方根比这个数的平方根小 D.一个数的立方根有两个,它们互为相反数
2.下列没有意义的是( )
A. B. C. D.
3.一个自然数a的算术平方根为x,那么的立方根是( )
A. B. C. D.
4.下列说法正确的是( )
A.一个数的立方根有两个,它们互为相反数 B.负数没有立方根
C.一个数有立方根,那么它的立方根一定为正数 D.一个数的立方根与这个数同号
题型02 求一个数的立方根
1.-的立方根是 ,的立方根是 .
2.下列说法正确的是( )
A.的立方根是 B.的立方根是
C.立方根等于本身的数是和 D.
3.立方根和平方根都等于本身的数是 .
4.的立方根的平方根是 .
题型03 利用开立方解方程
1.求下列各式中x的值:
(1);(2).(3).
2.求下列各式中x的值:
(1);(2);(3)
3.解方程:(1); (2);(3)
4.解下列方程
(1) ( 2) (3).
题型04 立方根的性质
1.先阅读材料,再解答问题.
,,.
,,.
,,.,
, , .
(1)完成上面的填空,并猜测互为相反数的两个数的立方根的关系为 .
(2)计算的值.
2.下列计算,错误的是( )
A. B. C. D.
3.已知,则的值为
4.【发现】①;②;③;④;……
根据上述等式反映的规律,请再写出一个等式:___________.
【归纳】等式①,②,③,④所反映的规律,可归纳为一个真命题:
对于任意两个有理数,,若_____,则;反之也成立.
【应用】根据上述所归纳的真命题,解决下列问题:若与的值互为相反数,求的值.
题型05 立方根小数点位数移动规律
1.(1)填表:
a 0.001 1 1000 1000000
1 10
由表你发现了:被开方数的小数点向右(或左)移动 位,其立方根的小数点向右(或左)移动 位;
(2)根据你发现的规律填空:①已知,则 ;②已知,则 .
(3)用铁皮制作一个封闭的正方体,它的体积为立方米,需要多大面积的铁皮?
2.已知,,,,,则 , .
3.【实践探究】
【问题情境】数学活动课上,老师带领同学们开展“运用规律求一个正数的算术平方根和立方根”的实践活动,同学们列出了表1中的算术平方根和表2中的立方根如下:
表1:
x … 0.0064 0.64 64 6400 640000 …
… 0.08 0.8 8 800 80 …
表2:
x … 0.000064 0.064 64 64000 64000000 …
… 0.04 0.4 4 40 400 …
【探索发现】(1)根据上述探究,可以得到被开方数和它的算术平方根和立方根之间小数点的变化规律是:若被开方数的小数点向右或向左移动 位,则它的算术平方根的小数点就相应地向右或向左移动 位;若被开方数的小数点向右或向左移动 位,它的立方根的小数点就相应地向右或向左移动 位.
【规律应用】(2)请运用上述规律,解答下列问题:
①已知,则 , ;
②若,求a, b的值.
(参考数据:)
(3)运用上述规律,你能根据的值求出的值吗? 请说明理由.
题型06 立方根的实际应用
1.如图1为一种球形容器(注:球的体积计算公式为),它受力均匀,承载能力强,且制作材料较为节省,在运输各种气体、液体、液化气时很受欢迎,图2为其示意图.现要生产两种容积分别为和的球形容器,则这两种容器的半径差(容器的厚度可忽略)为( )
A. B. C. D.
2.如图是小枫家的一块正方体积木,现测得它的体积为,那么64的立方根为( )
A.8 B. C.4 D.
3.小美和小丽分别制作了一个如图所示的正方体礼盒,已知小美制作的正方体礼盒的表面积为,而小丽制作的正方体礼盒的体积比小美制作的正方体礼盒的体积大,则小丽制作的正方体礼盒的表面积为( )
A. B. C. D.
4.如图是一块体积为343立方厘米的正方体铁块.
(1)求该正方体铁块的棱长;(2)现在工厂要将这块铁块熔化,重新锻造成两个棱长为3厘米的小正方体铁块和一个底面为正方形的长方体铁块.若长方体铁块的高为1厘米,求长方体铁块的底面正方形的边长.
题型07 算术平方根与立方根的综合运用
1.已知的立方根是的算术平方根是.
(1)求、的值;(2)求的平方根.
2.已知的平方根是,的立方根为.
(1)求a与b的值;(2)求的算术平方根和立方根.
3.已知是的算术平方根,的立方根是.
(1)求,的值;(2)求的立方根.
4.已知的立方根是3,的算术平方根是4.
(1)求a,b的值;(2)求的平方根.
题型08 阅读材料与新定义问题考法
1.我们已经从定义、表示、特征三个方面研究了平方根与立方根.实际上,数的方根的概念可以推广.类比平方根与立方根的学习,博学小组合作探究了次方根,下面是他们写的“次方根的学习档案”的部分内容.请认真阅读,并帮助其补充完整.
次方根的学习档案
定义:如果一个数的次方等于(是大于1的整数),即,那么这个数就叫做的次方根. 例如2是16的 . 求一个数的次方根的运算叫做 ,叫做 . 特征:根据次方根的意义,结合平方根与立方根的特征,探究发现正数、0和负数的次方根的特征如下: 正数的次方根是正数;0的次方根是 ;负数 .
2.我国著名数学家华罗庚有一次在飞机上看到他的助手阅读的杂志上有一道智力题:一个数是,求它的立方根.华罗庚脱口而出:.华罗庚是按照下面的方法算出的:由,,从而确定是两位数,由的个位上的数是,所以能确定的个位上的数是,如果划去后面的三位得到数,而,,由此就能确定的十位上的数是,所以的立方根是.模仿华罗庚的方法,请确定的立方根是 .
3.若n为自然数,对下面判断正确的是( )
A.一定无意义 B.一定有意义
C.若n为奇数,则必有意义 D.一定成立
4.已知变换:例如则的变换结果是( )
A. B. C. D.
参考答案
题型01 立方根的概念理解
1.A
【详解】解:∵一个正数有一个正的立方根,一个负数有一个负的立方根,0的立方根是0,
∴A选项说法正确;D选项说法不正确.
∵一个负数有一个负的立方根,但负数没有平方根,∴B选项说法不正确;
一个数的立方根不一定比这个数的平方根小,例如0的平方根和立方根相等,∴C选项说法不正确;
综上,说法正确的是A选项,故选:A.
2.A
【详解】解:A、,负数没有算术平方根,没有意义,符合题意;
B、表示的算术平方根,有意义,不符合题意;
C、表示的立平方根,有意义,不符合题意;
D、表示的立平方根,有意义,不符合题意;故选:A.
3.C
【详解】解:∵一个自然数的算术平方根为,∴,∴,
∴的立方根是,故选:C.
4.D
【详解】A、一个数的立方根只有一个,错误;B、负数有立方根,错误;
C、一个数有立方根,那么它的立方根不一定为正数,错误;
D、一个数的立方根与这个数同号,正确.故选:D.
题型02 求一个数的立方根
1.
【详解】解:的平方根是=;
∵,∴的立方根为=;故答案为:;.
2.D
【详解】解:、的立方根是,原选项说法错误,不符合题意;
、,的立方根是.原选项说法错误,不符合题意;
、立方根等于本身的数是,和,原选项说法错误,不符合题意;
、,原选项说法正确,符合题意;故选:.
3.0
【详解】解:立方根等于它本身的数是0,,平方根等于它本身的数是0,
所以立方根和平方根都等于本身的数是0.故答案为:0.
4.
【详解】解:∵,8的立方根是2∴的立方根是2,
∴的立方根的平方根是故答案为:.
题型03 利用开立方解方程
1.(1)解:∵,
∴,
∴,
∴;
(2),
,
,
;
(3)解:,
整理得,
∴,
∴.
2.解:(1)
∴.
(2)解:,
∴,
∴,
解得:.
(3)解:,
,
,
.
3.(1)解:
(2)解:
或.
(3)解:∵,
∴,
∴,
4.(1)解:,
∴,
∴,
∴;
(2)解:,
∴,
∴.
(3)解:,
,
,
.
题型04 立方根的性质
1.(1)解:,,;
∴互为相反数的两个数的立方根互为相反数;
故答案为:;;; ,相反数
(2)解:
.
2.D
【详解】解:A.,故此选项不合题意; B.,故此选项不合题意;
C.,故此选项不合题意; D. ,故此选项符合题意. 故选:D.
3.或2或3
【详解】解:∵,∴,
∴或,∴或或;故答案为:或2或3.
4.解:发现:根据题意;如(答案不唯一);
故答案为:(答案不唯一)
归纳:根据等式①,②,③,④所反映的规律,可归纳为一个真命题:
对于任意两个有理数,,若,则;反之也成立;故答案为:;
应用:与的值互为相反数;
, 解得,则.
题型05 立方根小数点位数移动规律
1.(1)解:填表:
a 0.001 1 1000 1000000
1 10
规律:数的小数点每移动三位,它的立方根的小数点就向相同方向移动一位;
(2)解:①∵,∴;
②∵∴;
(3)解:设正方体的棱长为米,则,,
(平方米),答:需要大约平方米的铁皮.
2. 1.285 2.342
【详解】解:,
故答案为:1.285;2.342
3.解:(1)由表格可得,若被开方数的小数点向右或向左移动2位,则它的算术平方根的小数点就相应地向右或向左移动1位;若被开方数的小数点向右或向左移动3位,它的立方根的小数点就相应地向右或向左移动1位,故答案为:2,1;3,1;
(2)①∵,∴,,故答案为:17.32,0.1442;
②∵,,∴,,
∴,,故答案为:200,0.8879;
(3)∵,∴,,∴不能求出的值.
题型06 立方根的实际应用
1.A
【详解】解:设一种球形容器的半径为,则,解得:
另一种球形容器的半径为,则,解得:
则这两种容器的半径差为:,故选:A
2.C
【详解】∵,∴64的立方根是4.故选:C.
3.B
【详解】解:设小美正方体棱长为,,得,,
小美制作的正方体礼盒的棱长为:,其体积为:,
小丽制作的正方体礼盒的体积为:,则小丽制作的正方体礼盒的棱长为:,
小丽制作的正方体礼盒的表面积为:;故选:B.
4.(1)解:由题意得,该正方体铁块的棱长为(厘米),∴该正方体铁块的棱长为7厘米.
(2)解:由题意,长方体的体积为:(立方厘米),
∴长方体的底面面积为:(平分厘米),
∴长方体铁块的底面正方形的边长为:(厘米),
∴长方体铁块的底面正方形的边长为17厘米.
题型07 算术平方根与立方根的综合运用
1.(1)解:的立方根是,的算术平方根是,
,,;
(2)解:当时,
17的平方根是,的平方根是.
2.(1)解:的平方根是,,解得;
又的立方根为,,解得;,.
(2)由(1)可知:,
的算术平方根为,的立方根为.
3.(1)解:是的算术平方根,,解得:,
的立方根是,∴,即解得:;
(2),,,的立方根是.
4.(1)解:∵的立方根是3,的算术平方根是4,
∴,,解得:,,故a的值为5,b的值为.
(2)解:由题知,,∵,∴的平方根是.
题型08 阅读材料与新定义问题考法
1.解∶,2是16的四次方根;
如果一个数x的n(n是大于|的整数)次方等于a,即,那么这个数x就叫做a的n次方根,求一个数a的n次方根的运算叫做开n次方,a叫做被开方数,n叫做根指数;正数的n次方根是正的;0的n次方根是0;负数不存在偶次方根,奇次方根为负数,
故答案为:四次方根;开次方;被开方数;0;没有偶次方根,奇次方根为负数.
2.
【详解】解:,,是两位数,
又只有个位上是的数的立方的个位上的数是,的个位上的数是,
如果划去后面的三位得到,而,,
十位上的数是,的立方根是,故答案为:.
3.C
【详解】解:当为偶数,时,有意义,
当为偶数时,必有意义,不一定成立,故C正确,ABD错误.故选:C.
4.C
【详解】解:由题意得,,,,故选:C.
同课章节目录
