人教版(2024)初中数学八 年级上册 13.1 三角形的概念 教学课件(共13张PPT)
文档属性
| 名称 | 人教版(2024)初中数学八 年级上册 13.1 三角形的概念 教学课件(共13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 301.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 10:00:40 | ||
图片预览




文档简介
(共13张PPT)
第十三章 三角形
13.1 三角形的概念
在小学,我们已经初步认识了三角形,本节我们将进一步学习三角形的有关概念及其符号表示,以及三角形的分类。
新课导入
学习目标
1.结合具体实例,进一步认识三角形的定义及其基本元素。
2.掌握三角形三个角和三条边之间的关系,会按角和边将三角形分类。
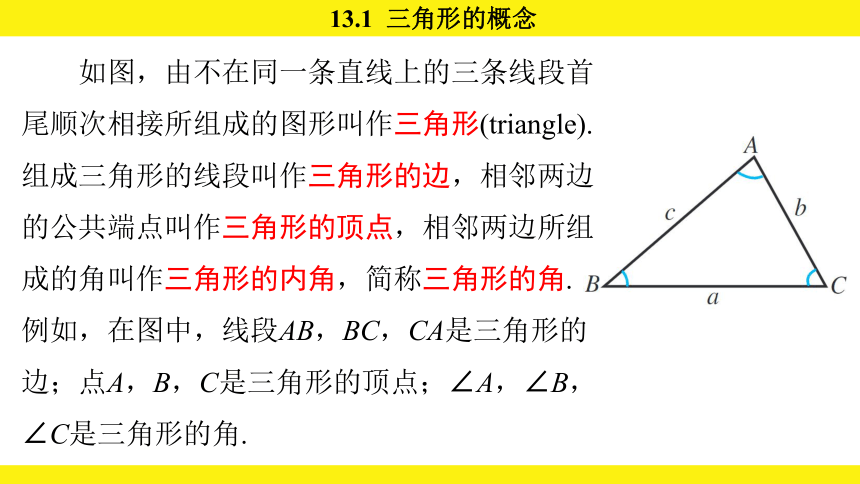
如图,由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫作三角形(triangle). 组成三角形的线段叫作三角形的边,相邻两边的公共端点叫作三角形的顶点,相邻两边所组成的角叫作三角形的内角,简称三角形的角. 例如,在图中,线段AB,BC,CA是三角形的边;点A,B,C是三角形的顶点;∠A,∠B,∠C是三角形的角.
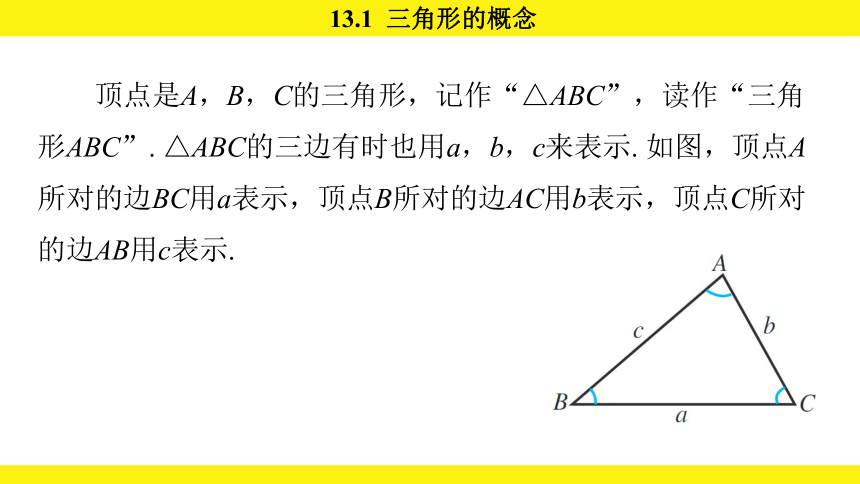
顶点是A,B,C的三角形,记作“△ABC”,读作“三角形ABC”. △ABC的三边有时也用a,b,c来表示. 如图,顶点A所对的边BC用a表示,顶点B所对的边AC用b表示,顶点C所对的边AB用c表示.
探究
我们知道,按照三个内角的大小,可以将三角形分为锐角三角形、直角三角形和钝角三角形. 如何按照边的关系对三角形进行分类呢 说说你的想法,并与同学交流.
在三角形中,有的三角形三边都不相等(图(1)),有的三角形有两边相等(2),有的三角形三边都相等(3).
(1)
(2)
(3)
有两边相等的三角形叫作等腰三角形(isosceles triangle),其中相等的两边叫作腰,另一边叫作底边,两腰的夹角叫作顶角,腰和底边的夹角叫作底角. 三边都相等的三角形叫作等边三角形(equilateral triangle),等边三角形是特殊的等腰三角形,即底边和腰相等的等腰三角形.
因此,可以先按“是否有边相等”,将三角形分成两类:三边都不相等的三角形和等腰三角形;再将等腰三角形分为底边和腰不相等的等腰三角形和等边三角形,得到三角形按边的相等关系分类如下:
典例精析
例 如图,在△ABC中,点D在边BC上,BD=AD=DC=AC
(1)写出以点C为顶点的三角形;
(2)写出以AB为边的三角形;
(3)找出图中的等腰三角形和等边三角形.
解:(1)以点C为顶点的三角形是△ABC,△ADC;
(2)以AB为边的三角形是△ABC,△ABD;
(3)等腰三角形是△ABD,△ADC;等边三角形是△ADC.
当堂练习
1.如图,在△ABC中,AB=BC=CA,点O在△ABC内,OA=OB=OC,找出图中的等腰三角形和等边三角形.
解:等腰三角形:△AOB,△AOC,
△BOC,△ ABC.
等边三角形:△ABC.
当堂练习
2.如图,在△ABC中,∠BAC是直角,AD⊥BC,垂足为D,点E在线段BD上,找出图中的锐角三角形、直角三角形和钝角三角形.
解:锐角三角形:△EAC.
直角三角形:△BAD,△EAD, △CAD,△BAC.
钝角三角形:△BAE.
谢谢观看
第十三章 三角形
13.1 三角形的概念
在小学,我们已经初步认识了三角形,本节我们将进一步学习三角形的有关概念及其符号表示,以及三角形的分类。
新课导入
学习目标
1.结合具体实例,进一步认识三角形的定义及其基本元素。
2.掌握三角形三个角和三条边之间的关系,会按角和边将三角形分类。
如图,由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫作三角形(triangle). 组成三角形的线段叫作三角形的边,相邻两边的公共端点叫作三角形的顶点,相邻两边所组成的角叫作三角形的内角,简称三角形的角. 例如,在图中,线段AB,BC,CA是三角形的边;点A,B,C是三角形的顶点;∠A,∠B,∠C是三角形的角.
顶点是A,B,C的三角形,记作“△ABC”,读作“三角形ABC”. △ABC的三边有时也用a,b,c来表示. 如图,顶点A所对的边BC用a表示,顶点B所对的边AC用b表示,顶点C所对的边AB用c表示.
探究
我们知道,按照三个内角的大小,可以将三角形分为锐角三角形、直角三角形和钝角三角形. 如何按照边的关系对三角形进行分类呢 说说你的想法,并与同学交流.
在三角形中,有的三角形三边都不相等(图(1)),有的三角形有两边相等(2),有的三角形三边都相等(3).
(1)
(2)
(3)
有两边相等的三角形叫作等腰三角形(isosceles triangle),其中相等的两边叫作腰,另一边叫作底边,两腰的夹角叫作顶角,腰和底边的夹角叫作底角. 三边都相等的三角形叫作等边三角形(equilateral triangle),等边三角形是特殊的等腰三角形,即底边和腰相等的等腰三角形.
因此,可以先按“是否有边相等”,将三角形分成两类:三边都不相等的三角形和等腰三角形;再将等腰三角形分为底边和腰不相等的等腰三角形和等边三角形,得到三角形按边的相等关系分类如下:
典例精析
例 如图,在△ABC中,点D在边BC上,BD=AD=DC=AC
(1)写出以点C为顶点的三角形;
(2)写出以AB为边的三角形;
(3)找出图中的等腰三角形和等边三角形.
解:(1)以点C为顶点的三角形是△ABC,△ADC;
(2)以AB为边的三角形是△ABC,△ABD;
(3)等腰三角形是△ABD,△ADC;等边三角形是△ADC.
当堂练习
1.如图,在△ABC中,AB=BC=CA,点O在△ABC内,OA=OB=OC,找出图中的等腰三角形和等边三角形.
解:等腰三角形:△AOB,△AOC,
△BOC,△ ABC.
等边三角形:△ABC.
当堂练习
2.如图,在△ABC中,∠BAC是直角,AD⊥BC,垂足为D,点E在线段BD上,找出图中的锐角三角形、直角三角形和钝角三角形.
解:锐角三角形:△EAC.
直角三角形:△BAD,△EAD, △CAD,△BAC.
钝角三角形:△BAE.
谢谢观看
同课章节目录
