人教版(2024)初中数学八年级上册 14.1 全等三角形及其性质 教学课件(共12张PPT)
文档属性
| 名称 | 人教版(2024)初中数学八年级上册 14.1 全等三角形及其性质 教学课件(共12张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 800.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 11:45:59 | ||
图片预览




文档简介
(共12张PPT)
第十四章 全等三角形
14.1 全等三角形及其性质
铺设地面的方砖、钢架桥中的三角形结构、足球比赛的场地……,都能在其中找到形状、大小相同的图形的形象. 形状、大小相同的图形是全等形.
新课导入
学习目标
1.理解全等形的定义,并能识别全等形.
2.理解全等三角形的定义,并能正确地找出全等三角形中的对应边、对应角.
3.掌握全等三角形的性质,并能运用这些性质进行简单的推理和计算,解决一些实际问题.
如下图,对开的大门、邮票、设计的图案中都有形状、大小想通的图形的形象,你能再举出一些类似的例子吗?
形状、大小相同的图形放在一起能够完全重合. 能够完全重合的两个图形叫做全等形.
能够完全重合的两个三角形叫做全等三角形(congruent triangles)
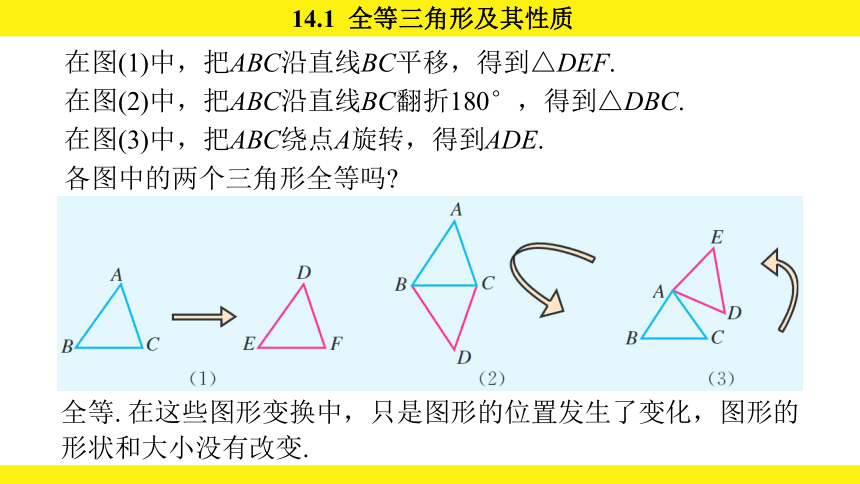
在图(1)中,把ABC沿直线BC平移,得到△DEF.
在图(2)中,把ABC沿直线BC翻折180°,得到△DBC.
在图(3)中,把ABC绕点A旋转,得到ADE.
各图中的两个三角形全等吗
全等. 在这些图形变换中,只是图形的位置发生了变化,图形的形状和大小没有改变.
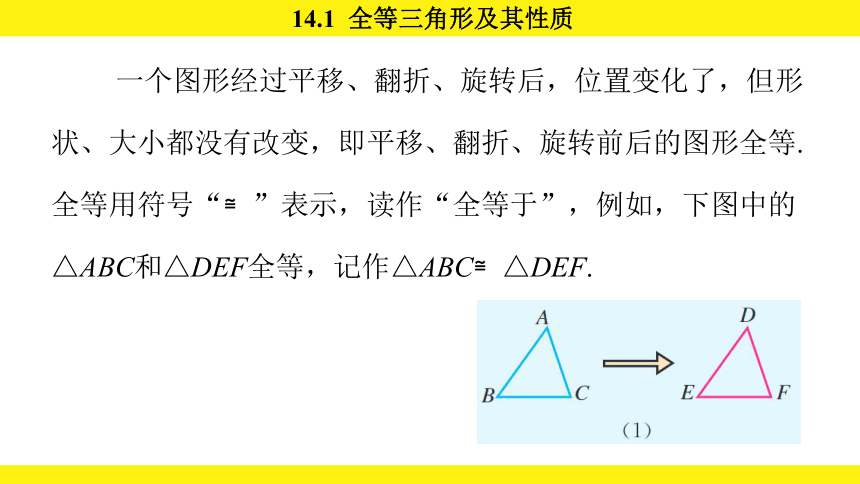
一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等. 全等用符号“≌”表示,读作“全等于”,例如,下图中的△ABC和△DEF全等,记作△ABC≌△DEF.
把两个全等的三角形重合到一起,重合的顶点叫作对应顶点,重合的边叫作对应边,重合的角叫作对应角. 例如,下图中△ABC≌△DEF,其中点A和点D,点B和点E,点C和点F是对应顶点;AB和DE,BC和EF,AC和DF是对应边;∠A和∠D,∠B和∠E,∠C和∠F是对应角.
记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
思考
下图中, △ABC≌△DEF,对应边有什么关系?对应角呢?其他两图中的全等三角形呢?
(1)(2)(3)中对应边相等,对应角相等。
全等三角形有这样的性质:
全等三角形的对应边相等,全等三角形的对应角相等.
典例精析
A
B
C
D
E
例 如图, △ABC≌△BAD,点A和点B,点C和点B是对应顶点,∠BAC=65°,
∠ABC=26°,AC,BD的延长线相交于点E. 求∠CBD,∠AEB的度数.
解:因为△ABC≌△BAD,
∴∠ABD=∠BAC=65°.
∴∠CBD=∠ABD-∠ABC = 65°-26°=39°.
在△AEB中,∠AEB+∠BAE+∠ABE=180°,
∴∠AEB=180°-∠ABE-∠ABE=180°-65°-65°=50°.
当堂练习
1.如图, △ABC≌△BDE,∠A和∠EBD,∠C和∠E是对应角. 说出这两个三角形的对应边和另一组对应角.
解:对应边:AC和BE,CB和ED,AB和BD.
另一组对应角:∠CBA和∠D.
A
B
C
D
E
当堂练习
2. 如图, △OCA≌△OBD ,点C和点B,点A和点D是对应顶点. 说出这两个三角形中相等的边和角.
解:相等的边:AC=DB,AO=DO,CO=BO.
相等的角:∠C=∠B,∠A=∠D,∠AOC=∠DOB.
谢谢观看
第十四章 全等三角形
14.1 全等三角形及其性质
铺设地面的方砖、钢架桥中的三角形结构、足球比赛的场地……,都能在其中找到形状、大小相同的图形的形象. 形状、大小相同的图形是全等形.
新课导入
学习目标
1.理解全等形的定义,并能识别全等形.
2.理解全等三角形的定义,并能正确地找出全等三角形中的对应边、对应角.
3.掌握全等三角形的性质,并能运用这些性质进行简单的推理和计算,解决一些实际问题.
如下图,对开的大门、邮票、设计的图案中都有形状、大小想通的图形的形象,你能再举出一些类似的例子吗?
形状、大小相同的图形放在一起能够完全重合. 能够完全重合的两个图形叫做全等形.
能够完全重合的两个三角形叫做全等三角形(congruent triangles)
在图(1)中,把ABC沿直线BC平移,得到△DEF.
在图(2)中,把ABC沿直线BC翻折180°,得到△DBC.
在图(3)中,把ABC绕点A旋转,得到ADE.
各图中的两个三角形全等吗
全等. 在这些图形变换中,只是图形的位置发生了变化,图形的形状和大小没有改变.
一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等. 全等用符号“≌”表示,读作“全等于”,例如,下图中的△ABC和△DEF全等,记作△ABC≌△DEF.
把两个全等的三角形重合到一起,重合的顶点叫作对应顶点,重合的边叫作对应边,重合的角叫作对应角. 例如,下图中△ABC≌△DEF,其中点A和点D,点B和点E,点C和点F是对应顶点;AB和DE,BC和EF,AC和DF是对应边;∠A和∠D,∠B和∠E,∠C和∠F是对应角.
记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
思考
下图中, △ABC≌△DEF,对应边有什么关系?对应角呢?其他两图中的全等三角形呢?
(1)(2)(3)中对应边相等,对应角相等。
全等三角形有这样的性质:
全等三角形的对应边相等,全等三角形的对应角相等.
典例精析
A
B
C
D
E
例 如图, △ABC≌△BAD,点A和点B,点C和点B是对应顶点,∠BAC=65°,
∠ABC=26°,AC,BD的延长线相交于点E. 求∠CBD,∠AEB的度数.
解:因为△ABC≌△BAD,
∴∠ABD=∠BAC=65°.
∴∠CBD=∠ABD-∠ABC = 65°-26°=39°.
在△AEB中,∠AEB+∠BAE+∠ABE=180°,
∴∠AEB=180°-∠ABE-∠ABE=180°-65°-65°=50°.
当堂练习
1.如图, △ABC≌△BDE,∠A和∠EBD,∠C和∠E是对应角. 说出这两个三角形的对应边和另一组对应角.
解:对应边:AC和BE,CB和ED,AB和BD.
另一组对应角:∠CBA和∠D.
A
B
C
D
E
当堂练习
2. 如图, △OCA≌△OBD ,点C和点B,点A和点D是对应顶点. 说出这两个三角形中相等的边和角.
解:相等的边:AC=DB,AO=DO,CO=BO.
相等的角:∠C=∠B,∠A=∠D,∠AOC=∠DOB.
谢谢观看
同课章节目录
