人教版(2024)初中数学八年级上册 15.2 画轴对称的图形 教学课件(共17张PPT)
文档属性
| 名称 | 人教版(2024)初中数学八年级上册 15.2 画轴对称的图形 教学课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 370.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 11:47:00 | ||
图片预览





文档简介
(共17张PPT)
第十五章 轴对称
15.2 画轴对称的图形
利用轴对称的定义,并结合轴对称的性质,可以画出与已知图形关于某条直线对称的图形,并进一步解决有关的问题.
新课导入
学习目标
1.掌握画一个轴对称图形的方法,能熟练地画出所求作的轴对称图形.
2.能利用轴对称进行图案设计,进一步体会图形中的对称美.
3.掌握平面直角坐标系中关于坐标轴对称的点特征,会表示一个点关于x轴和y轴对称的点的坐标.
4.能根据点的坐标画出一个图形关于x轴和y轴对称的轴对称图形.
思考
已知一个图形和一条直线,如何画出与这个图形关于这条直线对称的图形呢
可以通过折叠画出与一个图形成轴对称的图形. 如图,在一张半透明的纸的左边,画一只左脚印,把这张纸对折后描图,打开对折的纸,就可以得到与左脚印对称的右脚印,折痕所在直线就是它们的对称轴,并且连接任意一对对称点的线段被对称轴垂直平分.
几何图形都可以看作由点组成,对于一些规则的几何图形,与画平移后的图形类似,只要画出图形中的一些特殊点(如线段端点) 的对称点,连接这些对称点,就可以得到与原图形成轴对称的图形.
典例精析
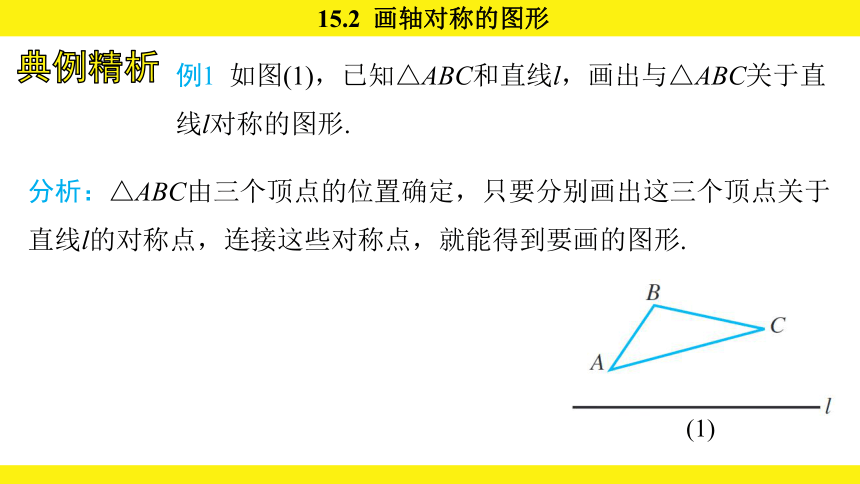
例1 如图(1),已知△ABC和直线l,画出与△ABC关于直线l对称的图形.
分析:△ABC由三个顶点的位置确定,只要分别画出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要画的图形.
(1)
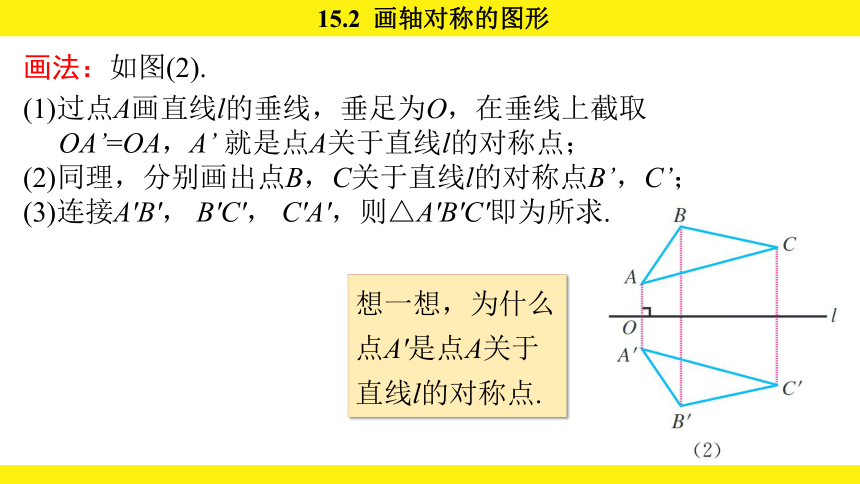
画法:如图(2).
(1)过点A画直线l的垂线,垂足为O,在垂线上截取
OA’=OA,A’ 就是点A关于直线l的对称点;
(2)同理,分别画出点B,C关于直线l的对称点B’,C’;
(3)连接A'B', B'C', C'A',则△A'B'C'即为所求.
想一想,为什么点A'是点A关于直线l的对称点.
1.如图,把各图形补成关于直线l对称的图形.
当堂练习
解:如图所示.
2.用纸片剪一个三角形,分别沿它一边的中线、高及其对角的平分线
对折,看看哪些部分能够重合,哪些部分不能重合.
当堂练习
解:沿它一边上的中线对折,这边所对的顶点重合,其他部分不一定重合;沿它一边上的高对折,这边所在直线重合,这边所对的顶点重合,其他部分不一定重合,沿这边对角的平分线对折,这个角的顶点及两边所在直线重合,其他部分不一定重合.
类似于平移,下面我们在平面直角坐标系中研究轴对称,研究关于坐标轴对称的图形的对称点坐标之间的关系.
探究
在如图13.2-4的平面直角坐标系中,画出下列已知点及其关于坐标轴的对称点,并把它们的坐标填入表格中,看一看每对对称点的坐标有怎样的规律,再和同学讨论一下.
2 3
-1 -2
-6 5
-1
4 0
-2 -3
1 2
6 -5
- 1
-4 0
再找几个点,分别画出它们关于x轴和y轴的对称点,检验一下你发现的规律.
归纳
点(x,y)关于x轴对称的点的坐标为(x, - y);
点(x,y)关于y轴对称的点的坐标为(-x, y).
在平面直角坐标系中,我们可以利用上述规律画出与一个图形关于x轴或y轴对称的图形. 对于一些规则的几何图形,只要先求出已知图形中的一些关键点 (如三角形的顶点) 关于坐标轴对称的点的坐标,描出并连接这些点,就可以得到与这个图形关于坐标轴对称的图形.
典例精析
例2 如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),C(-2,5),D(-5,4),画出与四边形ABCD关于y轴对称的图形.
解:点(x,y)关于y轴对称的点的坐标为(-x,y),因此四边形ABCD的顶点A,B,C,D关于y轴对称的点分别为A’(5,1),B’(2,1),C’(2,5),D’(5,4),依次连接A’B’,B’C’ ,C’D’,D’A’,就可得到与四边形ABCD关于y轴对称的四边形A’B’ C’D’.
类似地,请你在图中画出与四边形ABCD关于x轴对称的图形.
当堂练习
1.分别写出下列各点关于x轴和y轴对称的点的坐标:
(-2, 6), (1,-2), (1, 3), (-4,-2), (1, 0).
解:(-2, 6)关于x轴和y轴对称的点的坐标分别为(-2, -6), (2, 6);(1, -2)关于x轴和y轴对称的点的坐标分别为(1, 2), (-1, -2); (1, 3)关于x轴和y轴对称的点的坐标分别为(1,-3)(-1, 3); (-4, -2)关于x轴和y轴对称的点的坐标分别为(-4, 2), (4, -2); (1, 0)关于x轴和y轴对称的点的坐标分别为(1,0),(-1,0).
当堂练习
2.如图,△ABO关于x轴对称,点A的坐标为(1,-2),写出点B的坐标.
点B的坐标为(1, 2).
当堂练习
3.如图,利用关于坐标轴对称的点的坐标的特点,分别画出与△ABC关于x轴和y轴对称的图形.
解:如图所示.
△A'B'C'与△ABC 关于x轴对称,
△A"B"C"与△ABC关于y轴对称.
谢谢观看
第十五章 轴对称
15.2 画轴对称的图形
利用轴对称的定义,并结合轴对称的性质,可以画出与已知图形关于某条直线对称的图形,并进一步解决有关的问题.
新课导入
学习目标
1.掌握画一个轴对称图形的方法,能熟练地画出所求作的轴对称图形.
2.能利用轴对称进行图案设计,进一步体会图形中的对称美.
3.掌握平面直角坐标系中关于坐标轴对称的点特征,会表示一个点关于x轴和y轴对称的点的坐标.
4.能根据点的坐标画出一个图形关于x轴和y轴对称的轴对称图形.
思考
已知一个图形和一条直线,如何画出与这个图形关于这条直线对称的图形呢
可以通过折叠画出与一个图形成轴对称的图形. 如图,在一张半透明的纸的左边,画一只左脚印,把这张纸对折后描图,打开对折的纸,就可以得到与左脚印对称的右脚印,折痕所在直线就是它们的对称轴,并且连接任意一对对称点的线段被对称轴垂直平分.
几何图形都可以看作由点组成,对于一些规则的几何图形,与画平移后的图形类似,只要画出图形中的一些特殊点(如线段端点) 的对称点,连接这些对称点,就可以得到与原图形成轴对称的图形.
典例精析
例1 如图(1),已知△ABC和直线l,画出与△ABC关于直线l对称的图形.
分析:△ABC由三个顶点的位置确定,只要分别画出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要画的图形.
(1)
画法:如图(2).
(1)过点A画直线l的垂线,垂足为O,在垂线上截取
OA’=OA,A’ 就是点A关于直线l的对称点;
(2)同理,分别画出点B,C关于直线l的对称点B’,C’;
(3)连接A'B', B'C', C'A',则△A'B'C'即为所求.
想一想,为什么点A'是点A关于直线l的对称点.
1.如图,把各图形补成关于直线l对称的图形.
当堂练习
解:如图所示.
2.用纸片剪一个三角形,分别沿它一边的中线、高及其对角的平分线
对折,看看哪些部分能够重合,哪些部分不能重合.
当堂练习
解:沿它一边上的中线对折,这边所对的顶点重合,其他部分不一定重合;沿它一边上的高对折,这边所在直线重合,这边所对的顶点重合,其他部分不一定重合,沿这边对角的平分线对折,这个角的顶点及两边所在直线重合,其他部分不一定重合.
类似于平移,下面我们在平面直角坐标系中研究轴对称,研究关于坐标轴对称的图形的对称点坐标之间的关系.
探究
在如图13.2-4的平面直角坐标系中,画出下列已知点及其关于坐标轴的对称点,并把它们的坐标填入表格中,看一看每对对称点的坐标有怎样的规律,再和同学讨论一下.
2 3
-1 -2
-6 5
-1
4 0
-2 -3
1 2
6 -5
- 1
-4 0
再找几个点,分别画出它们关于x轴和y轴的对称点,检验一下你发现的规律.
归纳
点(x,y)关于x轴对称的点的坐标为(x, - y);
点(x,y)关于y轴对称的点的坐标为(-x, y).
在平面直角坐标系中,我们可以利用上述规律画出与一个图形关于x轴或y轴对称的图形. 对于一些规则的几何图形,只要先求出已知图形中的一些关键点 (如三角形的顶点) 关于坐标轴对称的点的坐标,描出并连接这些点,就可以得到与这个图形关于坐标轴对称的图形.
典例精析
例2 如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),C(-2,5),D(-5,4),画出与四边形ABCD关于y轴对称的图形.
解:点(x,y)关于y轴对称的点的坐标为(-x,y),因此四边形ABCD的顶点A,B,C,D关于y轴对称的点分别为A’(5,1),B’(2,1),C’(2,5),D’(5,4),依次连接A’B’,B’C’ ,C’D’,D’A’,就可得到与四边形ABCD关于y轴对称的四边形A’B’ C’D’.
类似地,请你在图中画出与四边形ABCD关于x轴对称的图形.
当堂练习
1.分别写出下列各点关于x轴和y轴对称的点的坐标:
(-2, 6), (1,-2), (1, 3), (-4,-2), (1, 0).
解:(-2, 6)关于x轴和y轴对称的点的坐标分别为(-2, -6), (2, 6);(1, -2)关于x轴和y轴对称的点的坐标分别为(1, 2), (-1, -2); (1, 3)关于x轴和y轴对称的点的坐标分别为(1,-3)(-1, 3); (-4, -2)关于x轴和y轴对称的点的坐标分别为(-4, 2), (4, -2); (1, 0)关于x轴和y轴对称的点的坐标分别为(1,0),(-1,0).
当堂练习
2.如图,△ABO关于x轴对称,点A的坐标为(1,-2),写出点B的坐标.
点B的坐标为(1, 2).
当堂练习
3.如图,利用关于坐标轴对称的点的坐标的特点,分别画出与△ABC关于x轴和y轴对称的图形.
解:如图所示.
△A'B'C'与△ABC 关于x轴对称,
△A"B"C"与△ABC关于y轴对称.
谢谢观看
同课章节目录
