人教版(2024)初中数学八年级上册 16.3 乘法公式 教学课件(共30张PPT)
文档属性
| 名称 | 人教版(2024)初中数学八年级上册 16.3 乘法公式 教学课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 11:48:30 | ||
图片预览











文档简介
(共30张PPT)
第十六章 整式的乘法
16.3 乘法公式
某些特殊形式的多项式相乘,可以写成公式的形式,当遇到相同形式的多项式相乘时,就可以直接运用公式写出结果.
新课导入
学习目标
1.掌握平方差公式,能熟练地运用平方差公式进行计算.
2.掌握完全平方公式,能熟练地运用完全平方公式进行计算.
3.能灵活地运用平方差公式和完全平方公式,并结合添括号法则进行整式的乘法运算.
探究
计算下列多项式的积,你能发现什么规律
(1)(x+1)(x-1)=________; (2)(m+2)(m-2)=________;
(3)(2x+1)(2x-1) =________.
16.3.1 平方差公式
x2-1
m2-4
4x2-1
规律:两个数的和与这两个数的差的积,等于这两个数的平方差.
上面的几个运算都是形如a+b的多项式与形如a-b的多项式相乘. 由于
所以,对于具有与此相同形式的多项式相乘,可以直接写出运算结果,即
也就是说,两个数的和与这两个数的差的积,等于这两个数的平方差.
这个公式叫作(乘法的)平方差公式.
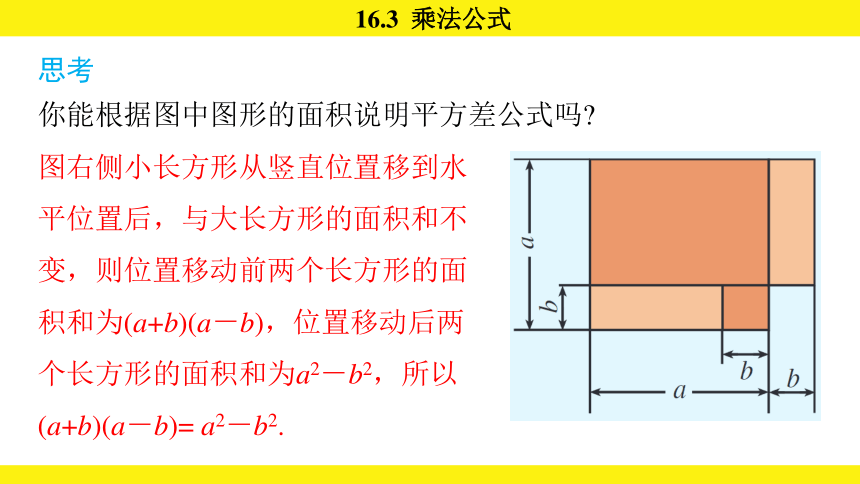
思考
你能根据图中图形的面积说明平方差公式吗
图右侧小长方形从竖直位置移到水平位置后,与大长方形的面积和不变,则位置移动前两个长方形的面积和为(a+b)(a-b),位置移动后两个长方形的面积和为a2-b2,所以(a+b)(a-b)= a2-b2.
典例精析
例1 运用平方差公式计算:
典例精析
例1 运用平方差公式计算:
典例精析
例2 计算:
(x-1) (x+1) (x2+1) (2) (y+2) (y-2)-(y-1) (y+5)
(3) 102×98
=(x2-1) (x2+1)
= x4-1
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= -4y+1
= 1002-22 = 10000-4
= 9996
当堂练习
1.下面的计算是否正确?如果不正确,应当怎样改正?
解:
当堂练习
2.计算:
当堂练习
2.计算:
当堂练习
3.运用平方差公式计算:
(1) 51×49; (2) 200×199.
= (50+1)×(50-1)
= 502-12
= 2500 -1
= 2499
= (200)×(200)
= 40000-
= 39999 .
16.3.2 完全平方公式
探究
计算下列多项式的积,你能发现什么规律
(p+1) = (p+1)(p+1)=_________;
(2)(m+2)2=(_______) (_______)=___________;
(3)(p-1)2=(_______) (_______)=___________;
(4)(m-2)2=(_______) (_______)=___________;
p2+2p+1
m+2
m+2
m2+4m+4
p-1
p2-2p+1
p-1
m-2
m2-4m+4
m-2
规律:两个数的和(或差)的平方,等于它们的平方和,加上(或减去)
它们的积的2倍.
上面的几个运算都是形如(a±b)2的多项式相乘,因为
所以,对于具有与此相同形式的多项式相乘,可以直接写出运算结果,即
也就是说,两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
这两个公式叫作(乘法的)完全平方公式.
(a+b)2=a2+2ab+b2是多项式乘法(a+b)·(p+q)中p=a,q=b的特殊情形.
你能根据图 1 和图 2 中图形的面积说明完全平方公式吗
图 1
图 2
由图 1可知,大正方形的边长是a+b,所以大正方形的面积为(a+b)2,又因为大正方形由一个边长为a的正方形、一个边长为b的正方形和两个长为a、宽为b的长方形组成,所以大正方形的面积为a2+2ab+b,因此(a+b)2 = a2+2ab+b2.
由图 2可知,深色大正方形的边长为a-b,所以深色大正方形的面积为(a-b)2 ,又因为深色大正方形的面积是大正方形的面积a2减去两个长为a、宽为b的长方形的面积之和,即a2 -2ab,此时多减了右上角深色小正方形的面积b2,再加上后可得深色大正方形的面积为 a2 -2ab+b2,因此(a-b)2 = a2-2ab+ b2.
典例精析
例3 运用完全平方公式计算:
典例精析
例4 运用完全平方公式计算:
思考
(a+b)2与(-a-b)2相等吗 (a-b)与(b-a)2 相等吗 (a-b)2 与a2-b2 相等吗 为什么
当堂练习
1.下面的计算是否正确 如果不正确,应当怎样改正
解:
2.运用完全平方公式计算:
当堂练习
解:
3.运用完全平方公式计算:
当堂练习
(1) 982;
(2) 70.52;
=(100-2)2
=1002-2×100×2+22
=10000-400+4
=9604
=(70+0.5)2
=702+70×0.5×2+0.52
=4900+70+0.25
=4970.25
运用乘法公式计算,有时要在式子中添括号. 在前面,我们学过去括号,由去括号法则可以得到
反过来,就得到
也就是说,添括号时,如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号.
典例精析
例5 运用乘法公式计算:
当堂练习
1.在等号右边的括号内填上适当的项.
b-c
b-c
-b+c
-b-c
当堂练习
2.运用乘法公式计算:
当堂练习
3.运用乘法公式计算:
谢谢观看
第十六章 整式的乘法
16.3 乘法公式
某些特殊形式的多项式相乘,可以写成公式的形式,当遇到相同形式的多项式相乘时,就可以直接运用公式写出结果.
新课导入
学习目标
1.掌握平方差公式,能熟练地运用平方差公式进行计算.
2.掌握完全平方公式,能熟练地运用完全平方公式进行计算.
3.能灵活地运用平方差公式和完全平方公式,并结合添括号法则进行整式的乘法运算.
探究
计算下列多项式的积,你能发现什么规律
(1)(x+1)(x-1)=________; (2)(m+2)(m-2)=________;
(3)(2x+1)(2x-1) =________.
16.3.1 平方差公式
x2-1
m2-4
4x2-1
规律:两个数的和与这两个数的差的积,等于这两个数的平方差.
上面的几个运算都是形如a+b的多项式与形如a-b的多项式相乘. 由于
所以,对于具有与此相同形式的多项式相乘,可以直接写出运算结果,即
也就是说,两个数的和与这两个数的差的积,等于这两个数的平方差.
这个公式叫作(乘法的)平方差公式.
思考
你能根据图中图形的面积说明平方差公式吗
图右侧小长方形从竖直位置移到水平位置后,与大长方形的面积和不变,则位置移动前两个长方形的面积和为(a+b)(a-b),位置移动后两个长方形的面积和为a2-b2,所以(a+b)(a-b)= a2-b2.
典例精析
例1 运用平方差公式计算:
典例精析
例1 运用平方差公式计算:
典例精析
例2 计算:
(x-1) (x+1) (x2+1) (2) (y+2) (y-2)-(y-1) (y+5)
(3) 102×98
=(x2-1) (x2+1)
= x4-1
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= -4y+1
= 1002-22 = 10000-4
= 9996
当堂练习
1.下面的计算是否正确?如果不正确,应当怎样改正?
解:
当堂练习
2.计算:
当堂练习
2.计算:
当堂练习
3.运用平方差公式计算:
(1) 51×49; (2) 200×199.
= (50+1)×(50-1)
= 502-12
= 2500 -1
= 2499
= (200)×(200)
= 40000-
= 39999 .
16.3.2 完全平方公式
探究
计算下列多项式的积,你能发现什么规律
(p+1) = (p+1)(p+1)=_________;
(2)(m+2)2=(_______) (_______)=___________;
(3)(p-1)2=(_______) (_______)=___________;
(4)(m-2)2=(_______) (_______)=___________;
p2+2p+1
m+2
m+2
m2+4m+4
p-1
p2-2p+1
p-1
m-2
m2-4m+4
m-2
规律:两个数的和(或差)的平方,等于它们的平方和,加上(或减去)
它们的积的2倍.
上面的几个运算都是形如(a±b)2的多项式相乘,因为
所以,对于具有与此相同形式的多项式相乘,可以直接写出运算结果,即
也就是说,两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
这两个公式叫作(乘法的)完全平方公式.
(a+b)2=a2+2ab+b2是多项式乘法(a+b)·(p+q)中p=a,q=b的特殊情形.
你能根据图 1 和图 2 中图形的面积说明完全平方公式吗
图 1
图 2
由图 1可知,大正方形的边长是a+b,所以大正方形的面积为(a+b)2,又因为大正方形由一个边长为a的正方形、一个边长为b的正方形和两个长为a、宽为b的长方形组成,所以大正方形的面积为a2+2ab+b,因此(a+b)2 = a2+2ab+b2.
由图 2可知,深色大正方形的边长为a-b,所以深色大正方形的面积为(a-b)2 ,又因为深色大正方形的面积是大正方形的面积a2减去两个长为a、宽为b的长方形的面积之和,即a2 -2ab,此时多减了右上角深色小正方形的面积b2,再加上后可得深色大正方形的面积为 a2 -2ab+b2,因此(a-b)2 = a2-2ab+ b2.
典例精析
例3 运用完全平方公式计算:
典例精析
例4 运用完全平方公式计算:
思考
(a+b)2与(-a-b)2相等吗 (a-b)与(b-a)2 相等吗 (a-b)2 与a2-b2 相等吗 为什么
当堂练习
1.下面的计算是否正确 如果不正确,应当怎样改正
解:
2.运用完全平方公式计算:
当堂练习
解:
3.运用完全平方公式计算:
当堂练习
(1) 982;
(2) 70.52;
=(100-2)2
=1002-2×100×2+22
=10000-400+4
=9604
=(70+0.5)2
=702+70×0.5×2+0.52
=4900+70+0.25
=4970.25
运用乘法公式计算,有时要在式子中添括号. 在前面,我们学过去括号,由去括号法则可以得到
反过来,就得到
也就是说,添括号时,如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号.
典例精析
例5 运用乘法公式计算:
当堂练习
1.在等号右边的括号内填上适当的项.
b-c
b-c
-b+c
-b-c
当堂练习
2.运用乘法公式计算:
当堂练习
3.运用乘法公式计算:
谢谢观看
同课章节目录
