人教版(2024)初中数学八年级上册 18.1 分式及其基本性质 教学课件(共37张PPT)
文档属性
| 名称 | 人教版(2024)初中数学八年级上册 18.1 分式及其基本性质 教学课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 11:48:57 | ||
图片预览










文档简介
(共37张PPT)
第十八章 分式
18.1 分式及其基本性质
我们知道,整式可以表示一些问题中的数量和数量关系. 在表示有些问题中的数量和数量关系时,还需要用到其他类型的代数式. 例如,一艘轮船在静水中的最大航速为30 km/h,它以最大航速沿江顺流航行90km所用的时间,在以最大航速逆流航行60 km/h 所用的时间相等,江水的流速为多少?
新课导入
设江水流速为v km/h,则轮船顺流航行90 km 所用时间为 h,逆流航行 60 km 所用的时间为 h,由方程 = 可以解出v的值.
像和这样,分母中含有字母的式子都是分式,像 = 这样,分母中含有未知数的方程是分式方程.
分式与分数具有类似的形式,我们类比分数学习分式的概念和基本性质.
学习目标
1.掌握分式的概念,明确分式与整式的区别与联系,能确定分式有(无)意义的条件,能确定使分式的值为0的条件.
2.理解分式的基本性质.
3.理解最简分式、最简公分母的概念,并能利用分式的基本性质对分式进行约分或通分.
18.1.1 从分数到分式
我们知道,两个数相除可以表示成分数的形式,例如,3÷4,(-7)÷2可,以分别表示成,,整式的除法也可以类似表示,例如,在章引言中,江水流速为v km/h,轮船顺流航行90km所用时间[90÷(30+v)]h 可以用 h来表示. 再来看几个问题.
思考
(1) 长方形的面积为 10,长为 7,则宽为__________;长方形的面积为S,长为a,则宽为__________.
(2) 在越野滑雪比赛中,若一名滑雪运动员在平地滑行a km 用时b h,则他的平均速度为__________ km/h;若他在上坡滑行a km 比在平地滑行同样的距离多用c h,则他的平均速度为__________ km/h.
在上面的问题中,填出的依次是,,,.
思考
式子,,以及本章引言中的式子,有什么共同点?它们与分数有什么相同点和不同点?
可以发现,这些式子与分数一样都是(即A÷B)的形式. 分数的分子A与分母B都是整数,而这些式子中的A与B都是整式,并且B中都含有字母.
一般地,如果A,B表示两个整式,并且B中含有字母,那么式子叫作分式(fraction). 在分式中,A叫作分子,B叫作分母.
分式是不同于整式的另一类代数式. 上面的,,,和 等都是分式. 因为分母可以表示不同的数,所以分式比分数更具有一般性. 例如,分数仅表示2÷3的商,而分式既可以表示2÷3,又可以表示(-5)÷2,8÷(-9)等.
思考
我们知道,要使分数有意义,分数中的分母不能为0. 要使分式有意义,分式中的分母应满足什么条件?
分式的分母表示除数,因为除数不能为0,所以分式的分母不能为0,即当B≠0时,分式才有意义.
典例精析
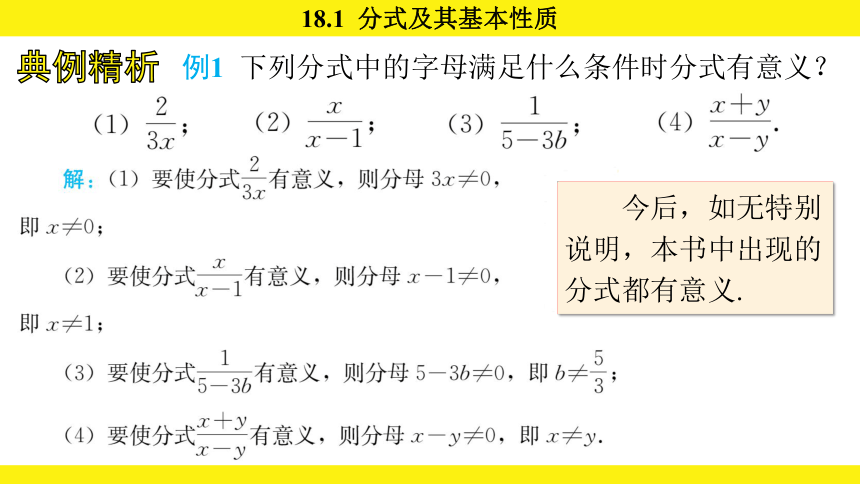
例1 下列分式中的字母满足什么条件时分式有意义?
今后,如无特别说明,本书中出现的分式都有意义.
当堂练习
1.列式表示下列各量:
某村有n个人,耕地 40 hm2,则人均耕地面积为________ hm2.
(2) △ABC的面积为S,边BC的长为a,则高AD为_________.
当堂练习
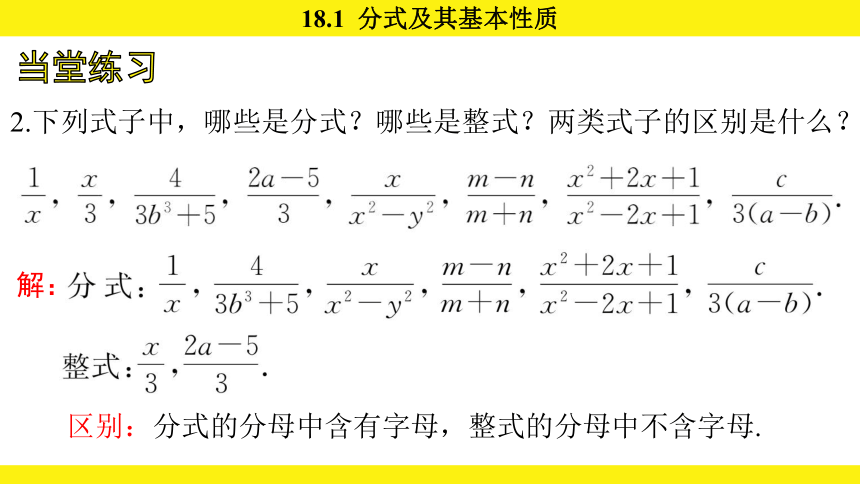
2.下列式子中,哪些是分式?哪些是整式?两类式子的区别是什么?
区别:分式的分母中含有字母,整式的分母中不含字母.
解:
当堂练习
3.下列分式中的字母满足什么条件时分式有意义
a≠0
x≠1
m≠-
x≠y
a≠
x≠-2
当堂练习
4.分式可以表示现实生活中的某些数量关系. 请你构造一个问题情境,使其中的数量关系可以用分式表示.
18.1.2 分式的基本性质
下面,我们类比分数的基本性质,学习分式的基本性质.
思考
回想一下,分数的基本性质是什么?请用符号表示分数的基本性质,并猜想分式的基本性质.
类比分数的基本性质:分数的分子与分母都乘(或除以)同一个不为0的数,分数的值不变. 分式具有基本性质:
上述性质可以用式子表示为
其中A,B,C (C≠0) 是整式.
典例精析
例2 下列等式,从左到右是如何运用分式的基本性质变形的?
(1) = (c≠0)
(2) = .
解:(1)分式的分子与分母乘同一个不等于0的整式c,分式的值不变,即 = = .
(2)分式的分子与分母除以同一个不等于0的整式x,分式的值不变,即 = = .
典例精析
例3 填空:
(2)
(3)
(4)
分析:观察等式,从左边到右边,分母(或分子)是如何变化的. 为保证分式的值不变,根据分式的基本性质. 分子(或分母)也应做同样的变化. 对于(1),分母x2y除以x2化为y,因此分子也需要除以x2;对于(2),分子除以 3x 化为x+y,因此分母也需要除以 3x.
(1)
2
典例精析
对于(3)(4),观察等式,从左边到右边,分母是如何变化的 相应地,分子应该如何变化
对于(3),分母ab乘a变为a2b,因此分子也需要乘a;
对于(4),分母a2乘b变为a2b,因此分子也需要乘b.
典例精析
(2) 因为
所以括号中应填2x.
(3) 因为
所以括号中应填a.
(4) 因为
所以括号中应填2ab-b2.
解:
(1) 因为
所以括号中应填x.
2
2
2
2
当堂练习
1.下列等式,从左到右是如何运用分式的基本性质变形的
解:(1)分式的分子、分母同乘x.
(2)分式的分子、分母同除以(x-y).
当堂练习
2.填空:
b
a+1
xy
2y
当堂练习
3.不改变分式的值,把下列各式中分子与分母的各项系数化为整数:
我们知道,分数的约分和通分在分数的运算中起着非常重要的作用. 类似地,分式的约分和通分在分式的运算中也有非常重要的作用. 下面讨论分式的约分和通分.
思考
联想分数的约分,由例3(1) (2),你能想出如何对分式进行约分吗?
先确定分式的分子、分母的公因式,再依据分式的基本性质,把分式的分子、分母的公因式约去.
与分数的约分类似,在例3 (1)中,我们利用分式的基本性质,约去 的分子和分母的公因式x2,不改变分式的值,把化为. 像这样,根据分式的基本性质,把一个分式的分子与分母的公因式约去,叫作分式的约分(reduction of a fraction). 经过约分后的分式,其分子与分母没有公因式. 像这样分子与分母没有公因式的分式,叫作最简分式. 同样地, 被约分成,也是最简分式.
分式的约分,一般要约去分子和分母所有的公因式,使所得结果成为最简分式或者整式.
典例精析
例4 约分:
分析:为约分,要先找出分子和分母的公因式.
典例精析
如果分式的分子或分母是多项式,分解因式对约分有什么作用?
因为约分是将分子、分母中的公因式约去,所以当分子或分母是多项式时,只有先利用因式分解将多项式化为乘积形式才能找到分子、分母的公因式.
思考
联想分数的通分,由例3(3) (4),你能想出如何对分式进行约分吗?
由于分数的通分是先确定各分数分母的最小公倍数作为最简公分母,然后将各分数运用分数的基本性质转化为与原来分数相等的同分母的分数,因此类比分数的通分方法,可以联想到分式的通分也是需要先确定出各个分式分母的最简公分母,然后仿照分数的通分进行分式的通分.
与分数的约分类似,在例3 (3) (4)中,我们利用分式的基本性质,将分子和分母同乘适当的整式,不改变分式的值,把 化为 化成分母相同的分式. 像这样,根据分式的基本性质,把几个异分母的分式分别化成与原来的分式相等的同分母的分式,叫作分式的通分 (reduction of fractions to a common denominator).
分式的通分,关键是确定几个分式的公分母,一般取各分母的所有因式的最高次幂的积作公分母,它叫作最简公分母.
典例精析
例5 通分:
(1) 与 (2) 与
分析:为通分,要先确定最简公分母,对于 (1),因为分母系数的最小公倍数是6,字母a,b,c的最高次幂分别是a2,b2,c,所以最简公分母是6a2b2c;对于 (2),分母是多项式,要先分解因式,再通分.
典例精析
解:(1) 最简公分母是6a2b2c.
= = ,
= = .
(2) 最简公分母是2(x-5) (x+5).
= = ,
= = .
典例精析
如果分式的分母是多项式,分解因式对于通分有什么作用
如果分式的分母是多项式,通分时先分解因式,可明显看出它们的最简公分母,使通分过程不易出错.
思考
分数和分式在约分和通分的做法上有什么共同点?这些做法的根据是什么?
分数和分式的约分都是约去公因数或公因式,化分数为最简分数或整数、化分式为最简分式或整式;分数和分式的通分都是将异分母化为同分母.
这些做法的根据是分数、分式的基本性质.
当堂练习
1.约分:
当堂练习
2.通分:
解:最简公分母是abc.
解:最简公分母是4b2d.
当堂练习
2.通分:
解:最简公分母是ab(x+2).
解:最简公分母是(x-y) (x+y)2.
谢谢观看
第十八章 分式
18.1 分式及其基本性质
我们知道,整式可以表示一些问题中的数量和数量关系. 在表示有些问题中的数量和数量关系时,还需要用到其他类型的代数式. 例如,一艘轮船在静水中的最大航速为30 km/h,它以最大航速沿江顺流航行90km所用的时间,在以最大航速逆流航行60 km/h 所用的时间相等,江水的流速为多少?
新课导入
设江水流速为v km/h,则轮船顺流航行90 km 所用时间为 h,逆流航行 60 km 所用的时间为 h,由方程 = 可以解出v的值.
像和这样,分母中含有字母的式子都是分式,像 = 这样,分母中含有未知数的方程是分式方程.
分式与分数具有类似的形式,我们类比分数学习分式的概念和基本性质.
学习目标
1.掌握分式的概念,明确分式与整式的区别与联系,能确定分式有(无)意义的条件,能确定使分式的值为0的条件.
2.理解分式的基本性质.
3.理解最简分式、最简公分母的概念,并能利用分式的基本性质对分式进行约分或通分.
18.1.1 从分数到分式
我们知道,两个数相除可以表示成分数的形式,例如,3÷4,(-7)÷2可,以分别表示成,,整式的除法也可以类似表示,例如,在章引言中,江水流速为v km/h,轮船顺流航行90km所用时间[90÷(30+v)]h 可以用 h来表示. 再来看几个问题.
思考
(1) 长方形的面积为 10,长为 7,则宽为__________;长方形的面积为S,长为a,则宽为__________.
(2) 在越野滑雪比赛中,若一名滑雪运动员在平地滑行a km 用时b h,则他的平均速度为__________ km/h;若他在上坡滑行a km 比在平地滑行同样的距离多用c h,则他的平均速度为__________ km/h.
在上面的问题中,填出的依次是,,,.
思考
式子,,以及本章引言中的式子,有什么共同点?它们与分数有什么相同点和不同点?
可以发现,这些式子与分数一样都是(即A÷B)的形式. 分数的分子A与分母B都是整数,而这些式子中的A与B都是整式,并且B中都含有字母.
一般地,如果A,B表示两个整式,并且B中含有字母,那么式子叫作分式(fraction). 在分式中,A叫作分子,B叫作分母.
分式是不同于整式的另一类代数式. 上面的,,,和 等都是分式. 因为分母可以表示不同的数,所以分式比分数更具有一般性. 例如,分数仅表示2÷3的商,而分式既可以表示2÷3,又可以表示(-5)÷2,8÷(-9)等.
思考
我们知道,要使分数有意义,分数中的分母不能为0. 要使分式有意义,分式中的分母应满足什么条件?
分式的分母表示除数,因为除数不能为0,所以分式的分母不能为0,即当B≠0时,分式才有意义.
典例精析
例1 下列分式中的字母满足什么条件时分式有意义?
今后,如无特别说明,本书中出现的分式都有意义.
当堂练习
1.列式表示下列各量:
某村有n个人,耕地 40 hm2,则人均耕地面积为________ hm2.
(2) △ABC的面积为S,边BC的长为a,则高AD为_________.
当堂练习
2.下列式子中,哪些是分式?哪些是整式?两类式子的区别是什么?
区别:分式的分母中含有字母,整式的分母中不含字母.
解:
当堂练习
3.下列分式中的字母满足什么条件时分式有意义
a≠0
x≠1
m≠-
x≠y
a≠
x≠-2
当堂练习
4.分式可以表示现实生活中的某些数量关系. 请你构造一个问题情境,使其中的数量关系可以用分式表示.
18.1.2 分式的基本性质
下面,我们类比分数的基本性质,学习分式的基本性质.
思考
回想一下,分数的基本性质是什么?请用符号表示分数的基本性质,并猜想分式的基本性质.
类比分数的基本性质:分数的分子与分母都乘(或除以)同一个不为0的数,分数的值不变. 分式具有基本性质:
上述性质可以用式子表示为
其中A,B,C (C≠0) 是整式.
典例精析
例2 下列等式,从左到右是如何运用分式的基本性质变形的?
(1) = (c≠0)
(2) = .
解:(1)分式的分子与分母乘同一个不等于0的整式c,分式的值不变,即 = = .
(2)分式的分子与分母除以同一个不等于0的整式x,分式的值不变,即 = = .
典例精析
例3 填空:
(2)
(3)
(4)
分析:观察等式,从左边到右边,分母(或分子)是如何变化的. 为保证分式的值不变,根据分式的基本性质. 分子(或分母)也应做同样的变化. 对于(1),分母x2y除以x2化为y,因此分子也需要除以x2;对于(2),分子除以 3x 化为x+y,因此分母也需要除以 3x.
(1)
2
典例精析
对于(3)(4),观察等式,从左边到右边,分母是如何变化的 相应地,分子应该如何变化
对于(3),分母ab乘a变为a2b,因此分子也需要乘a;
对于(4),分母a2乘b变为a2b,因此分子也需要乘b.
典例精析
(2) 因为
所以括号中应填2x.
(3) 因为
所以括号中应填a.
(4) 因为
所以括号中应填2ab-b2.
解:
(1) 因为
所以括号中应填x.
2
2
2
2
当堂练习
1.下列等式,从左到右是如何运用分式的基本性质变形的
解:(1)分式的分子、分母同乘x.
(2)分式的分子、分母同除以(x-y).
当堂练习
2.填空:
b
a+1
xy
2y
当堂练习
3.不改变分式的值,把下列各式中分子与分母的各项系数化为整数:
我们知道,分数的约分和通分在分数的运算中起着非常重要的作用. 类似地,分式的约分和通分在分式的运算中也有非常重要的作用. 下面讨论分式的约分和通分.
思考
联想分数的约分,由例3(1) (2),你能想出如何对分式进行约分吗?
先确定分式的分子、分母的公因式,再依据分式的基本性质,把分式的分子、分母的公因式约去.
与分数的约分类似,在例3 (1)中,我们利用分式的基本性质,约去 的分子和分母的公因式x2,不改变分式的值,把化为. 像这样,根据分式的基本性质,把一个分式的分子与分母的公因式约去,叫作分式的约分(reduction of a fraction). 经过约分后的分式,其分子与分母没有公因式. 像这样分子与分母没有公因式的分式,叫作最简分式. 同样地, 被约分成,也是最简分式.
分式的约分,一般要约去分子和分母所有的公因式,使所得结果成为最简分式或者整式.
典例精析
例4 约分:
分析:为约分,要先找出分子和分母的公因式.
典例精析
如果分式的分子或分母是多项式,分解因式对约分有什么作用?
因为约分是将分子、分母中的公因式约去,所以当分子或分母是多项式时,只有先利用因式分解将多项式化为乘积形式才能找到分子、分母的公因式.
思考
联想分数的通分,由例3(3) (4),你能想出如何对分式进行约分吗?
由于分数的通分是先确定各分数分母的最小公倍数作为最简公分母,然后将各分数运用分数的基本性质转化为与原来分数相等的同分母的分数,因此类比分数的通分方法,可以联想到分式的通分也是需要先确定出各个分式分母的最简公分母,然后仿照分数的通分进行分式的通分.
与分数的约分类似,在例3 (3) (4)中,我们利用分式的基本性质,将分子和分母同乘适当的整式,不改变分式的值,把 化为 化成分母相同的分式. 像这样,根据分式的基本性质,把几个异分母的分式分别化成与原来的分式相等的同分母的分式,叫作分式的通分 (reduction of fractions to a common denominator).
分式的通分,关键是确定几个分式的公分母,一般取各分母的所有因式的最高次幂的积作公分母,它叫作最简公分母.
典例精析
例5 通分:
(1) 与 (2) 与
分析:为通分,要先确定最简公分母,对于 (1),因为分母系数的最小公倍数是6,字母a,b,c的最高次幂分别是a2,b2,c,所以最简公分母是6a2b2c;对于 (2),分母是多项式,要先分解因式,再通分.
典例精析
解:(1) 最简公分母是6a2b2c.
= = ,
= = .
(2) 最简公分母是2(x-5) (x+5).
= = ,
= = .
典例精析
如果分式的分母是多项式,分解因式对于通分有什么作用
如果分式的分母是多项式,通分时先分解因式,可明显看出它们的最简公分母,使通分过程不易出错.
思考
分数和分式在约分和通分的做法上有什么共同点?这些做法的根据是什么?
分数和分式的约分都是约去公因数或公因式,化分数为最简分数或整数、化分式为最简分式或整式;分数和分式的通分都是将异分母化为同分母.
这些做法的根据是分数、分式的基本性质.
当堂练习
1.约分:
当堂练习
2.通分:
解:最简公分母是abc.
解:最简公分母是4b2d.
当堂练习
2.通分:
解:最简公分母是ab(x+2).
解:最简公分母是(x-y) (x+y)2.
谢谢观看
同课章节目录
