人教版(2024)初中数学八年级上册 18.4 整数指数幂 教学课件(共23张PPT)
文档属性
| 名称 | 人教版(2024)初中数学八年级上册 18.4 整数指数幂 教学课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 691.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 11:49:33 | ||
图片预览








文档简介
(共23张PPT)
第十八章 分式
18.4 整数指数幂
随着我们认识的数的范围不断扩大,数的运算也在不断推广. 例如,加法运算从非负整数范围推广到非负有理数范围,再到有理数范围. 同样地,对于幂的运算an,是否也可以从正整数指数幂推广到更大的范围呢?下面,我们从追溯幂的符号的演变开始.
新课导入
学习目标
1.理解负整数指数幂的意义,会进行简单的整数范围内的幂的运算.
2.能根据负整数指数幂的定义,运用科学计数法表示小于1的正数.
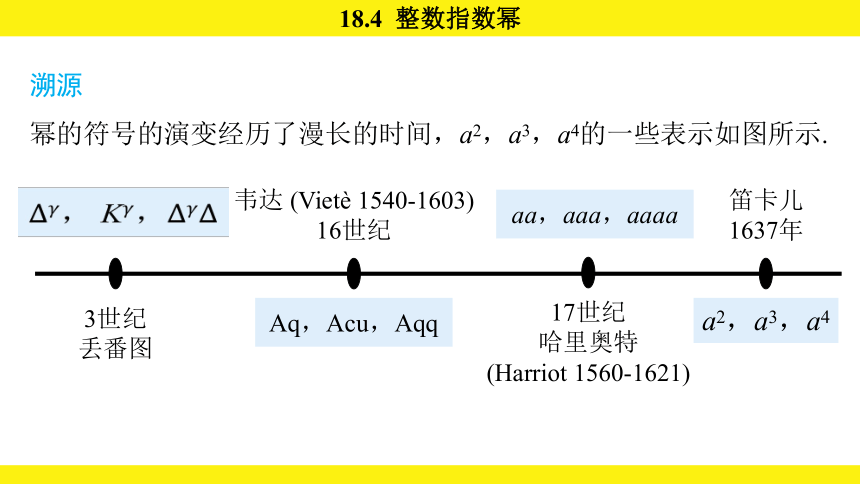
溯源
幂的符号的演变经历了漫长的时间,a2,a3,a4的一些表示如图所示.
, K,
3世纪
丢番图
韦达 (Vietè 1540-1603)
16世纪
Aq,Acu,Aqq
aa,aaa,aaaa
17世纪
哈里奥特
(Harriot 1560-1621)
笛卡儿
1637年
a2,a3,a4
an这种幂的符号不仅简单、利于运算,而且有助于幂的运算的推广. 1676年,牛顿 (Newton,1643 — 1727) 提出了一个设想:“因为数学家将aa,aaa,aaaa,…写成a2,a3,a4, …,所以我将,,,…写成a-1,a- 2,a- 3 ,….”
思考
你认为牛顿的这个设想合理吗?也就是说,如果am中的m可以是负整数,那么负整数指数幂am表示什么
由分式的约分可知,当a≠0时,
另一方面,如果把正整数指数幂的运算性质am÷an=am-n (a≠0,m,n是正整数,m>n) 中的条件m>n去掉,即假设这个性质对于像 a3÷a5 的情形也能使用,则有
引入负整数指数幂后,指数的取值范围就推广到全体整数.
今后,如无特别说明,本单元中涉及的负整数指数幂的底数均不为0.
思考
引入负整数指数和0指数后,正整数指数幂的运算性质
am·an=am+n (m, n是正整数) ①
能否推广到m,n是任意整数的情形?
am·an=am+n (m, n是正整数),这条性质能推广到m,n是任意整数的情形.
我们从特殊情形入手进行研究. 例如,
探究
类似地,你可以用负整数指数幂或0指数幂对于其他四个正整数指数幂的运算性质
(am)n=amn(m, n是正整数),
(ab)=anbn (n是正整数),
am÷an=am-n (a≠0,m, n是正整数, m>n),
()n = (n是正整数)
进行尝试,看看这些性质在整数指数幂范围内是否还适用.
随着指数的取值范围由正整数推广到全体整数,其他正整数指数幂的运算性质也推广到整数指数幂.
典例精析
例1 计算:
根据整数指数幂的运算性质,当m,n为整数时,
因此
即同底数幂的除法am÷an可以转化为同底数幂的乘法am·a-n.
特别地,
所以
即商的乘方
可以转化为积的乘方
于是,整数指数幂的运算性质可以归纳为:
当堂练习
1. 填空:
1
1
1
当堂练习
2. 计算:
我们已经知道,一些较大的数适合用科学记数法表示. 例如,光速约为3×108m/s,太阳半径约为6.96×105km,有了负整数指数幂后,小于1的正数也可以用科学记数法表示. 例如,0.000 01=1×10-5,0.000 025 7 = 2.57×10-5,0.000 000 025 7=2.57×10-8等.
一般地,小于1的正数可以用科学记数法表示为a×10-n的形式,其中1 ≤ a <10,n是正整数,这种形式更便于比较数的大小和运算,例如,自然科学和生活中经常用到的分(d)、厘(c)、毫(m)、微(μ)、纳(n)等国际单位制词头,其中微对应10-6,纳对应10-9. 微米(μm)、纳米(nm)都是长度单位1μm = 10-6m, 1 nm = 10-9 m.
思考
对于一个小于1的正小数,如果小数点后至第一个非0数字前有8个0,用科学记数法表示这个数时,10的指数是多少?如果有m个0呢
10的指数是-9;如果有m个0,那么10的指数是-m-1.
典例精析
例2 碳纳米管是一种前沿纳米材料,有很多神奇的特性. 它是由呈六边形排列的碳原子构成的单层或多层的同轴圆管,其直径一般为2~20nm.通常一根头发丝的直径约为70μm, 一根头发丝的直径大约是碳纳米管直径的多少倍?
解: 70μm = 70×10-6m,2nm = 2×10-9 m,20nm=20×10-9m.
(70×10-6)÷(2×10-9) = 3.5×104.
(70×10-6)÷(20×10-9) = 3.5×103.
因此,一根头发丝的直径是碳纳米管直径的3.5×103 ~ 3.5×104倍.
当堂练习
1.用科学记数法表示下列数:
=1×10-9
=1.2×10-3
=3.45×10-7
=1.08×10-8
当堂练习
2.计算:
谢谢观看
第十八章 分式
18.4 整数指数幂
随着我们认识的数的范围不断扩大,数的运算也在不断推广. 例如,加法运算从非负整数范围推广到非负有理数范围,再到有理数范围. 同样地,对于幂的运算an,是否也可以从正整数指数幂推广到更大的范围呢?下面,我们从追溯幂的符号的演变开始.
新课导入
学习目标
1.理解负整数指数幂的意义,会进行简单的整数范围内的幂的运算.
2.能根据负整数指数幂的定义,运用科学计数法表示小于1的正数.
溯源
幂的符号的演变经历了漫长的时间,a2,a3,a4的一些表示如图所示.
, K,
3世纪
丢番图
韦达 (Vietè 1540-1603)
16世纪
Aq,Acu,Aqq
aa,aaa,aaaa
17世纪
哈里奥特
(Harriot 1560-1621)
笛卡儿
1637年
a2,a3,a4
an这种幂的符号不仅简单、利于运算,而且有助于幂的运算的推广. 1676年,牛顿 (Newton,1643 — 1727) 提出了一个设想:“因为数学家将aa,aaa,aaaa,…写成a2,a3,a4, …,所以我将,,,…写成a-1,a- 2,a- 3 ,….”
思考
你认为牛顿的这个设想合理吗?也就是说,如果am中的m可以是负整数,那么负整数指数幂am表示什么
由分式的约分可知,当a≠0时,
另一方面,如果把正整数指数幂的运算性质am÷an=am-n (a≠0,m,n是正整数,m>n) 中的条件m>n去掉,即假设这个性质对于像 a3÷a5 的情形也能使用,则有
引入负整数指数幂后,指数的取值范围就推广到全体整数.
今后,如无特别说明,本单元中涉及的负整数指数幂的底数均不为0.
思考
引入负整数指数和0指数后,正整数指数幂的运算性质
am·an=am+n (m, n是正整数) ①
能否推广到m,n是任意整数的情形?
am·an=am+n (m, n是正整数),这条性质能推广到m,n是任意整数的情形.
我们从特殊情形入手进行研究. 例如,
探究
类似地,你可以用负整数指数幂或0指数幂对于其他四个正整数指数幂的运算性质
(am)n=amn(m, n是正整数),
(ab)=anbn (n是正整数),
am÷an=am-n (a≠0,m, n是正整数, m>n),
()n = (n是正整数)
进行尝试,看看这些性质在整数指数幂范围内是否还适用.
随着指数的取值范围由正整数推广到全体整数,其他正整数指数幂的运算性质也推广到整数指数幂.
典例精析
例1 计算:
根据整数指数幂的运算性质,当m,n为整数时,
因此
即同底数幂的除法am÷an可以转化为同底数幂的乘法am·a-n.
特别地,
所以
即商的乘方
可以转化为积的乘方
于是,整数指数幂的运算性质可以归纳为:
当堂练习
1. 填空:
1
1
1
当堂练习
2. 计算:
我们已经知道,一些较大的数适合用科学记数法表示. 例如,光速约为3×108m/s,太阳半径约为6.96×105km,有了负整数指数幂后,小于1的正数也可以用科学记数法表示. 例如,0.000 01=1×10-5,0.000 025 7 = 2.57×10-5,0.000 000 025 7=2.57×10-8等.
一般地,小于1的正数可以用科学记数法表示为a×10-n的形式,其中1 ≤ a <10,n是正整数,这种形式更便于比较数的大小和运算,例如,自然科学和生活中经常用到的分(d)、厘(c)、毫(m)、微(μ)、纳(n)等国际单位制词头,其中微对应10-6,纳对应10-9. 微米(μm)、纳米(nm)都是长度单位1μm = 10-6m, 1 nm = 10-9 m.
思考
对于一个小于1的正小数,如果小数点后至第一个非0数字前有8个0,用科学记数法表示这个数时,10的指数是多少?如果有m个0呢
10的指数是-9;如果有m个0,那么10的指数是-m-1.
典例精析
例2 碳纳米管是一种前沿纳米材料,有很多神奇的特性. 它是由呈六边形排列的碳原子构成的单层或多层的同轴圆管,其直径一般为2~20nm.通常一根头发丝的直径约为70μm, 一根头发丝的直径大约是碳纳米管直径的多少倍?
解: 70μm = 70×10-6m,2nm = 2×10-9 m,20nm=20×10-9m.
(70×10-6)÷(2×10-9) = 3.5×104.
(70×10-6)÷(20×10-9) = 3.5×103.
因此,一根头发丝的直径是碳纳米管直径的3.5×103 ~ 3.5×104倍.
当堂练习
1.用科学记数法表示下列数:
=1×10-9
=1.2×10-3
=3.45×10-7
=1.08×10-8
当堂练习
2.计算:
谢谢观看
同课章节目录
