人教版(2024)初中数学八年级上册13.3 三角形的内角与外角 教学课件(共27张PPT)
文档属性
| 名称 | 人教版(2024)初中数学八年级上册13.3 三角形的内角与外角 教学课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 00:00:00 | ||
图片预览





文档简介
(共27张PPT)
第十三章 三角形
13.3 三角形的内角与外角
与边一样,三角形的角也是构成三角形的元素. 本节我们学习三角形的三个内角之间的关系,并进一步学习其他与三角形有关的角.
新课导入
学习目标
1.会运用平行线的性质与平角的定义证明三角形的内角和等于180°,
体会转化思想在数学中的运用.
2.掌握三角形内角和定理.
3.掌握直角三角形的性质和判定.
4.了解三角形外角的定义,掌握三角形外角的性质.
13.2.1 三角形的内角
在小学,通过度量或剪拼,我们已经知道三角形的内角和等于180°,这样的方法获得的结论可靠吗
由于测量常常有误差,这样验证三角形的内角和等于180°,不能完全令人信服;又由于形状不同的三角形有无数个,我们不可能用上述方法一一验证所有三角形的内角和等于180°. 因此,需要通过推理的方法去证明:任意一个三角形的内角和等于180°.
探究
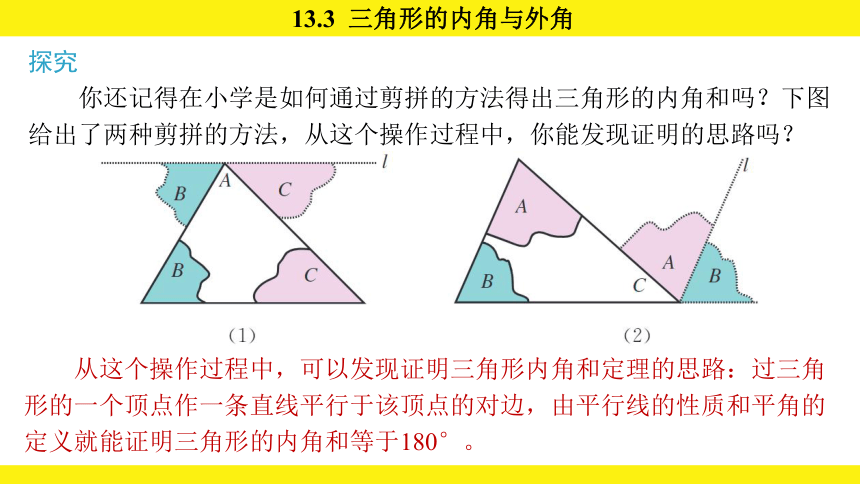
你还记得在小学是如何通过剪拼的方法得出三角形的内角和吗?下图给出了两种剪拼的方法,从这个操作过程中,你能发现证明的思路吗?
从这个操作过程中,可以发现证明三角形内角和定理的思路:过三角形的一个顶点作一条直线平行于该顶点的对边,由平行线的性质和平角的定义就能证明三角形的内角和等于180°。
在图(1)中,将△ABC的∠B和∠C剪下,分别拼在∠A的左右,三个角合起来形成一个平角,出现一条过点A的直线l,移动后的∠B和∠C各有一条边在直线上. 想一想,直线l与△ABC的边BC有什么关系 你能由这个图想出证明“三角形的内角和等于180°”的方法吗
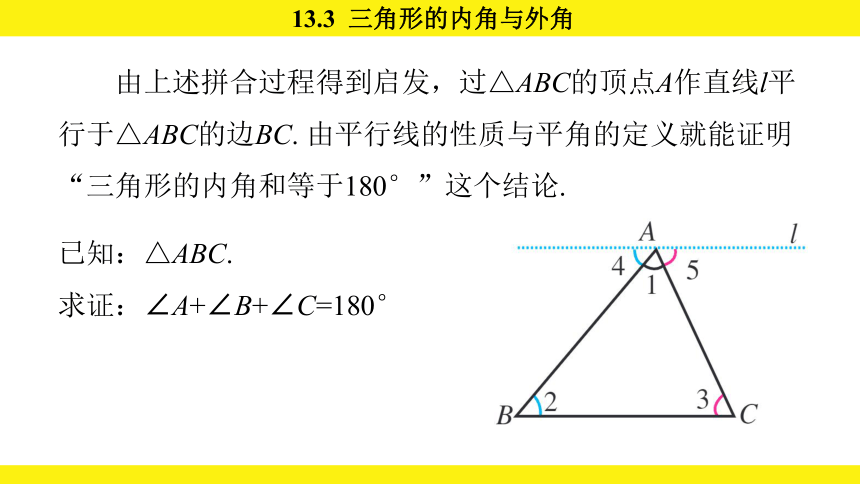
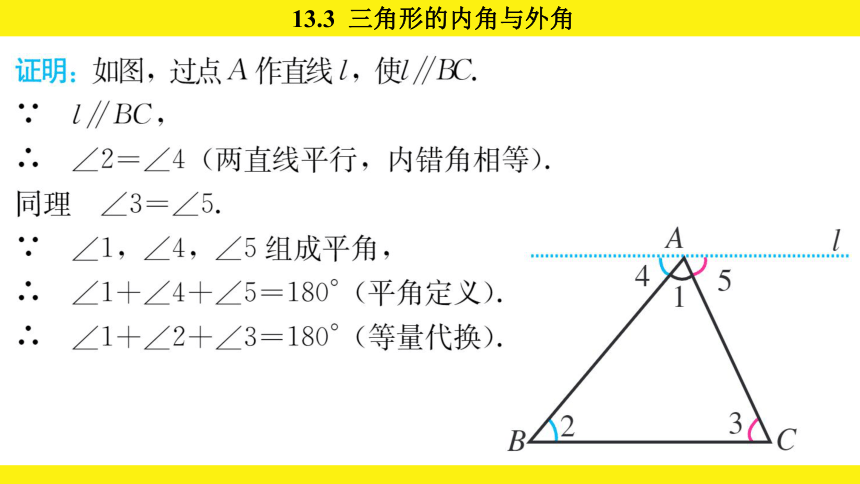
由上述拼合过程得到启发,过△ABC的顶点A作直线l平行于△ABC的边BC. 由平行线的性质与平角的定义就能证明“三角形的内角和等于180°”这个结论.
已知:△ABC.
求证:∠A+∠B+∠C=180°
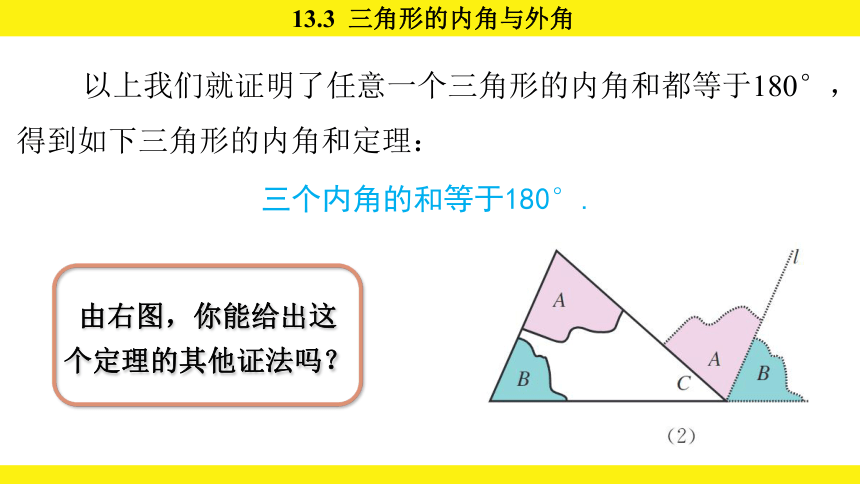
以上我们就证明了任意一个三角形的内角和都等于180°,得到如下三角形的内角和定理:
三个内角的和等于180°.
由右图,你能给出这个定理的其他证法吗?
典例精析
例1 如图,在△ABC中,∠BAC=∠B=75°,AD是△ABC的角平分线. 求∠ADB的度数.
典例精析
例2 右图是A,B,C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向. 从B岛看A,C两岛的视角∠ABC是多少度 从岛看A,B两岛的视角∠ACB呢
分析:A,B,C三岛的连线构成△ABC,所求的∠ACB是△ABC的一个内角. 如果能求出∠CAB,∠ABC,就能求出∠ACB.
你还能给出其他解法吗
当堂练习
1. 如图,从A处观测C处的仰角∠CAD=30°,从B处观测C处的仰角∠CBD=45°. 从C处观测A,B两处的视角∠ACB是多少度
解:∠BCD=180°-∠CBD-∠D=180°-45°-90° =45°,
∠ACD=180°-∠A -∠D=180°-30°-90°= 60°,
∴∠ACB = ∠ACD -∠BCD = 60°-45°= 15°.
当堂练习
2. 如图,在△ABC中,∠A=40°,求∠B+∠C+∠ADE+∠AED的度数.
解:∵∠A=40°,
∵∠ADE+∠AED=180°-40°=140°.
同理,∠C+∠B=180°-∠A=180°-40°=140°.
∴∠B+∠C+∠ADE+∠AED =140+140°=280°.
利用三角形的内角和定理,可以得到一些特殊三角形的内角的关系.
如图,在直角三角形ABC中,∠C=90°,
由三角形的内角和定理,得
典例精析
例2 如图,∠C=∠D=90°,AD,BC相交于点E,∠CAE与∠DBE有什么关系?为什么?
思考
我们知道,如果一个三角形是直角三角形,那么这个三角形有两个角互余. 反过来,有两个角互余的三角形是直角三角形吗 请你说说理由.
有两个角互余的三角形是直角三角形.
理由如下:
如图所示,
∵∠A+∠B=90°
∴∠C=180° -(∠A+∠B)
=180° -90°-90°.
△ABC是直角三角形.
由三角形的内角和定理可得 (请你自己完成证明):
有两个角互余的三角形是直角三角形.
当堂练习
1.如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D. ∠ACD与∠B有什么关系 为什么
解:∠ACD=∠B.
∵∠ACB=90°,
∴∠A+∠B=90°.
∵CD⊥AB,∴∠ADC=90°,
∴∠A+∠ACD=90°.
∴∠ACD=∠B.
当堂练习
2.如图,在△ABC中,∠C=90°,点D,E分别在边AB,AC上,且∠1=∠2,△ADE是直角三角形吗 为什么
解:△ADE是直角三角形.
∵∠C=90°, ∴∠A+∠2=90°.
∵∠1=∠2, ∴∠A+∠1=90°,
∴∠ADE=90°.
∴ △ADE是直角三角形.
13.3.2 三角形的外角
如图,把△ABC的一边BC延长,得到∠ACD. 像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角,
思考
如图,在△ABC中,∠A=70°,∠B=60°. ∠ACD是△ABC的一个外角. 能由∠A,∠B求出∠ACD吗 如果能,∠ACD与∠A, ∠B有什么关系
任意一个三角形的一个外角与它不相邻的两个内角是否都有这种关系
解:能,∠ACD=∠A+∠B
如图,
任意一个三角形的一个外角与和它不相邻的两个内角都有这种关系.
一般地,由三角形内角和定理可以推出下面的推论(请你自己证明):
三角形的外角等于与它不相邻的两个内角的和
典例精析
例4 如图,∠BAE,∠CBF,∠ACD是△ABC 的三个外角, 它们的和是多少
你还能给出其他解法吗
当堂练习
说出下列图形中∠1和∠2的度数:
解:(1)∠2=80°+60°=140 ° ,
∠1=180°-∠2=180°-140°=40°.
(2)∠2=30°+40°=70°,∠1=180° -70°=110°.
(3)∠1=90°-40°= 50°,∠2=180°-40°=140°.
解:(4)∠2=180°-40°-70°=70 ° ,
∠1= (180°-∠2)=55°.
(5) ∠1=60°+20°=80°,
∠2=180°-∠1-60°=180°-80°-60°=40°.
(6)∠1=90°-30°=60°,∠2=∠90°-∠1 =30°.
谢谢观看
第十三章 三角形
13.3 三角形的内角与外角
与边一样,三角形的角也是构成三角形的元素. 本节我们学习三角形的三个内角之间的关系,并进一步学习其他与三角形有关的角.
新课导入
学习目标
1.会运用平行线的性质与平角的定义证明三角形的内角和等于180°,
体会转化思想在数学中的运用.
2.掌握三角形内角和定理.
3.掌握直角三角形的性质和判定.
4.了解三角形外角的定义,掌握三角形外角的性质.
13.2.1 三角形的内角
在小学,通过度量或剪拼,我们已经知道三角形的内角和等于180°,这样的方法获得的结论可靠吗
由于测量常常有误差,这样验证三角形的内角和等于180°,不能完全令人信服;又由于形状不同的三角形有无数个,我们不可能用上述方法一一验证所有三角形的内角和等于180°. 因此,需要通过推理的方法去证明:任意一个三角形的内角和等于180°.
探究
你还记得在小学是如何通过剪拼的方法得出三角形的内角和吗?下图给出了两种剪拼的方法,从这个操作过程中,你能发现证明的思路吗?
从这个操作过程中,可以发现证明三角形内角和定理的思路:过三角形的一个顶点作一条直线平行于该顶点的对边,由平行线的性质和平角的定义就能证明三角形的内角和等于180°。
在图(1)中,将△ABC的∠B和∠C剪下,分别拼在∠A的左右,三个角合起来形成一个平角,出现一条过点A的直线l,移动后的∠B和∠C各有一条边在直线上. 想一想,直线l与△ABC的边BC有什么关系 你能由这个图想出证明“三角形的内角和等于180°”的方法吗
由上述拼合过程得到启发,过△ABC的顶点A作直线l平行于△ABC的边BC. 由平行线的性质与平角的定义就能证明“三角形的内角和等于180°”这个结论.
已知:△ABC.
求证:∠A+∠B+∠C=180°
以上我们就证明了任意一个三角形的内角和都等于180°,得到如下三角形的内角和定理:
三个内角的和等于180°.
由右图,你能给出这个定理的其他证法吗?
典例精析
例1 如图,在△ABC中,∠BAC=∠B=75°,AD是△ABC的角平分线. 求∠ADB的度数.
典例精析
例2 右图是A,B,C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向. 从B岛看A,C两岛的视角∠ABC是多少度 从岛看A,B两岛的视角∠ACB呢
分析:A,B,C三岛的连线构成△ABC,所求的∠ACB是△ABC的一个内角. 如果能求出∠CAB,∠ABC,就能求出∠ACB.
你还能给出其他解法吗
当堂练习
1. 如图,从A处观测C处的仰角∠CAD=30°,从B处观测C处的仰角∠CBD=45°. 从C处观测A,B两处的视角∠ACB是多少度
解:∠BCD=180°-∠CBD-∠D=180°-45°-90° =45°,
∠ACD=180°-∠A -∠D=180°-30°-90°= 60°,
∴∠ACB = ∠ACD -∠BCD = 60°-45°= 15°.
当堂练习
2. 如图,在△ABC中,∠A=40°,求∠B+∠C+∠ADE+∠AED的度数.
解:∵∠A=40°,
∵∠ADE+∠AED=180°-40°=140°.
同理,∠C+∠B=180°-∠A=180°-40°=140°.
∴∠B+∠C+∠ADE+∠AED =140+140°=280°.
利用三角形的内角和定理,可以得到一些特殊三角形的内角的关系.
如图,在直角三角形ABC中,∠C=90°,
由三角形的内角和定理,得
典例精析
例2 如图,∠C=∠D=90°,AD,BC相交于点E,∠CAE与∠DBE有什么关系?为什么?
思考
我们知道,如果一个三角形是直角三角形,那么这个三角形有两个角互余. 反过来,有两个角互余的三角形是直角三角形吗 请你说说理由.
有两个角互余的三角形是直角三角形.
理由如下:
如图所示,
∵∠A+∠B=90°
∴∠C=180° -(∠A+∠B)
=180° -90°-90°.
△ABC是直角三角形.
由三角形的内角和定理可得 (请你自己完成证明):
有两个角互余的三角形是直角三角形.
当堂练习
1.如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D. ∠ACD与∠B有什么关系 为什么
解:∠ACD=∠B.
∵∠ACB=90°,
∴∠A+∠B=90°.
∵CD⊥AB,∴∠ADC=90°,
∴∠A+∠ACD=90°.
∴∠ACD=∠B.
当堂练习
2.如图,在△ABC中,∠C=90°,点D,E分别在边AB,AC上,且∠1=∠2,△ADE是直角三角形吗 为什么
解:△ADE是直角三角形.
∵∠C=90°, ∴∠A+∠2=90°.
∵∠1=∠2, ∴∠A+∠1=90°,
∴∠ADE=90°.
∴ △ADE是直角三角形.
13.3.2 三角形的外角
如图,把△ABC的一边BC延长,得到∠ACD. 像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角,
思考
如图,在△ABC中,∠A=70°,∠B=60°. ∠ACD是△ABC的一个外角. 能由∠A,∠B求出∠ACD吗 如果能,∠ACD与∠A, ∠B有什么关系
任意一个三角形的一个外角与它不相邻的两个内角是否都有这种关系
解:能,∠ACD=∠A+∠B
如图,
任意一个三角形的一个外角与和它不相邻的两个内角都有这种关系.
一般地,由三角形内角和定理可以推出下面的推论(请你自己证明):
三角形的外角等于与它不相邻的两个内角的和
典例精析
例4 如图,∠BAE,∠CBF,∠ACD是△ABC 的三个外角, 它们的和是多少
你还能给出其他解法吗
当堂练习
说出下列图形中∠1和∠2的度数:
解:(1)∠2=80°+60°=140 ° ,
∠1=180°-∠2=180°-140°=40°.
(2)∠2=30°+40°=70°,∠1=180° -70°=110°.
(3)∠1=90°-40°= 50°,∠2=180°-40°=140°.
解:(4)∠2=180°-40°-70°=70 ° ,
∠1= (180°-∠2)=55°.
(5) ∠1=60°+20°=80°,
∠2=180°-∠1-60°=180°-80°-60°=40°.
(6)∠1=90°-30°=60°,∠2=∠90°-∠1 =30°.
谢谢观看
同课章节目录
