人教版(2024)初中数学八年级上册16.1 幂的运算 教学课件(共19张PPT)
文档属性
| 名称 | 人教版(2024)初中数学八年级上册16.1 幂的运算 教学课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 927.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
第十六章 整式的乘法
16.1 幂的运算
整式的乘法是代数运算以及解决许多数学问题的重要基础. 我们可以类比数的运算,以运算律为基础,研究整式的乘法运算.
幂的运算是整式的乘法的基础,学习整式的乘法,需要先学习幂的运算性质.
新课导入
学习目标
1.掌握同底数幂的乘法.
2.掌握幂的乘方、积的乘方的运算性质,并能熟练地运用这些运算性质进行有关计算.
16.1.1 同底数幂的乘法
问题 一种电子计算机每秒可进行1亿亿(1016)次运算,它工作103s可进行多少次运算?
它工作103 s可进行运算的次数为1016×103 . 怎样计算1016×103呢?
搭载国产芯片的“神威·太湖之光”是世界上首台运行速度超过每秒10亿亿次的超级计算机.
探究
根据乘方的意义填空,观察计算结果,你能发现什么规律
(1)105×102=10( );
(2)a3·a2=a( );
(3)5m×5( ) (m,n是正整数).
7
5
m+n
规律:同底数幂相乘,底数不变,指数相加.
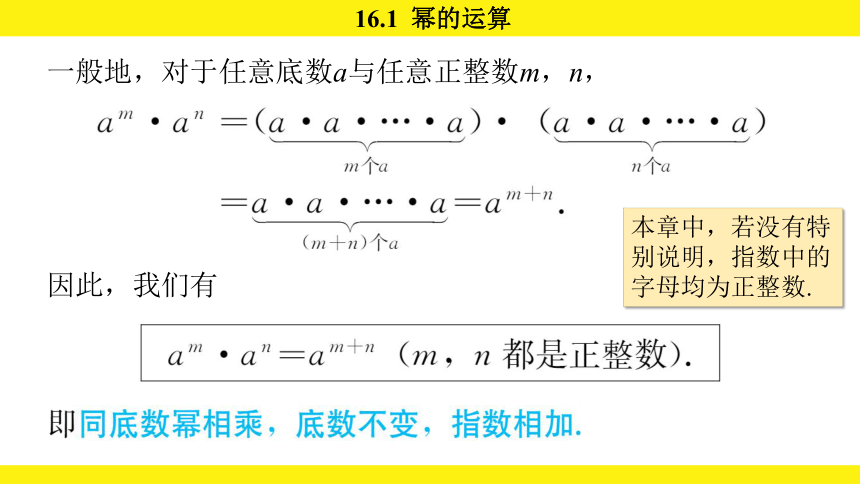
一般地,对于任意底数a与任意正整数m,n,
因此,我们有
本章中,若没有特别说明,指数中的字母均为正整数.
典例精析
三个或三个以上同底数幂相乘,也具有这一性质.
当堂练习
1.下面的计算是否正确?如果不正确,应当怎样改正?
(1)a3·a2=a6; (2)a·a3=a0+3=a3;
(3)m3·m3=2m3; (4)x2m·x4n-2=x2m+4n-2.
不正确,改正:a5
不正确,改正:a4
不正确,改正:m6
正确
当堂练习
2.下面的计算是否正确?如果不正确,应当怎样改正?
(1)a2·a6; (2) b3·b;
(3)y2n·yn+1; (4)(-)×(-)2×(-)3.
=a8
=b6
=y3n+1
=(-)6 =
16.1.2 幂的乘方与积的乘方
探究
根据乘方的意义及同底数幂的运算性质填空,观察计算结果,你能发现什么规律
(1) (32)3=32×32×32=3( );
(2) (a2)3=__________=a( );
(3) (am)3=__________=a( ).
6
a2·a2·a2
6
am·am·am
3m
规律:幂的乘方,底数不变,指数相乘.
一般地,对于任意底数a与任意正整数m,n,
因此,我们有
典例精析
探究
填空,运算过程用到哪些运算律?运算结果有什么规律
2
2
(ab)·(ab)·(ab)
(a·a·a)·(b·b·b)
3
3
运算过程用到了乘法交换律和乘法结合律.
规律:积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
三个或三个以上的积的乘方,也具有这一性质.
典例精析
当堂练习
1.下面的计算是否正确?如果不正确,应当怎样改正
(1) (a5)2=a7; (2) (ab2)3; (3)(-2a)2=-4a2.
解:(1)不正确,改正:a10.
(2)不正确,改正:a3b6.
(3)不正确,改正:4a2.
当堂练习
2.计算:
(1) (103)3; (2) (x3)2; (3) -(xm)5; (4) (a2)3· a5.
解:(1) (103)3 = 109. (2) (x3)2 = x6.
(3) -(xm)5 = -x5m. (4) (a2)3· a5 = a11.
当堂练习
2.计算:
(1) (ab)4; (2) (-3×102)3; (3) (-xy2)3; (4) 2(ab2)3· 2ab2.
解:
谢谢观看
第十六章 整式的乘法
16.1 幂的运算
整式的乘法是代数运算以及解决许多数学问题的重要基础. 我们可以类比数的运算,以运算律为基础,研究整式的乘法运算.
幂的运算是整式的乘法的基础,学习整式的乘法,需要先学习幂的运算性质.
新课导入
学习目标
1.掌握同底数幂的乘法.
2.掌握幂的乘方、积的乘方的运算性质,并能熟练地运用这些运算性质进行有关计算.
16.1.1 同底数幂的乘法
问题 一种电子计算机每秒可进行1亿亿(1016)次运算,它工作103s可进行多少次运算?
它工作103 s可进行运算的次数为1016×103 . 怎样计算1016×103呢?
搭载国产芯片的“神威·太湖之光”是世界上首台运行速度超过每秒10亿亿次的超级计算机.
探究
根据乘方的意义填空,观察计算结果,你能发现什么规律
(1)105×102=10( );
(2)a3·a2=a( );
(3)5m×5( ) (m,n是正整数).
7
5
m+n
规律:同底数幂相乘,底数不变,指数相加.
一般地,对于任意底数a与任意正整数m,n,
因此,我们有
本章中,若没有特别说明,指数中的字母均为正整数.
典例精析
三个或三个以上同底数幂相乘,也具有这一性质.
当堂练习
1.下面的计算是否正确?如果不正确,应当怎样改正?
(1)a3·a2=a6; (2)a·a3=a0+3=a3;
(3)m3·m3=2m3; (4)x2m·x4n-2=x2m+4n-2.
不正确,改正:a5
不正确,改正:a4
不正确,改正:m6
正确
当堂练习
2.下面的计算是否正确?如果不正确,应当怎样改正?
(1)a2·a6; (2) b3·b;
(3)y2n·yn+1; (4)(-)×(-)2×(-)3.
=a8
=b6
=y3n+1
=(-)6 =
16.1.2 幂的乘方与积的乘方
探究
根据乘方的意义及同底数幂的运算性质填空,观察计算结果,你能发现什么规律
(1) (32)3=32×32×32=3( );
(2) (a2)3=__________=a( );
(3) (am)3=__________=a( ).
6
a2·a2·a2
6
am·am·am
3m
规律:幂的乘方,底数不变,指数相乘.
一般地,对于任意底数a与任意正整数m,n,
因此,我们有
典例精析
探究
填空,运算过程用到哪些运算律?运算结果有什么规律
2
2
(ab)·(ab)·(ab)
(a·a·a)·(b·b·b)
3
3
运算过程用到了乘法交换律和乘法结合律.
规律:积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
三个或三个以上的积的乘方,也具有这一性质.
典例精析
当堂练习
1.下面的计算是否正确?如果不正确,应当怎样改正
(1) (a5)2=a7; (2) (ab2)3; (3)(-2a)2=-4a2.
解:(1)不正确,改正:a10.
(2)不正确,改正:a3b6.
(3)不正确,改正:4a2.
当堂练习
2.计算:
(1) (103)3; (2) (x3)2; (3) -(xm)5; (4) (a2)3· a5.
解:(1) (103)3 = 109. (2) (x3)2 = x6.
(3) -(xm)5 = -x5m. (4) (a2)3· a5 = a11.
当堂练习
2.计算:
(1) (ab)4; (2) (-3×102)3; (3) (-xy2)3; (4) 2(ab2)3· 2ab2.
解:
谢谢观看
同课章节目录
