【暑假应用题专项训练】(含解析)第1-7单元-数学五年级下册苏教版
文档属性
| 名称 | 【暑假应用题专项训练】(含解析)第1-7单元-数学五年级下册苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 666.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 17:09:26 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【暑假应用题专项训练】第1-7单元-数学五年级下册苏教版
1.A轿车的售价是16.8万元,比B轿车售价的3倍还多3.9万元。B轿车的售价是多少万元?
2.2023年5月28日,我国首架具有自主知识产权的干线客机圆满完成载客首飞。一架客机的机身总长38.9米,比机高的4倍少8.9米,一架客机机高多少米?(列方程解答)
3.小明买了一张长方形的游戏拼图,周长是38.4厘米。已知长是宽的3倍,这张拼图宽多少厘米?(列方程解答)
4.甲、乙两列火车同时从两地相对开出,经过3.6小时相遇,这时甲车比乙车多行18千米。已知乙车每小时行90千米,甲车每小时行多少千米?(列方程解答)
5.下面是一张不小心被弄脏的电费缴费单。
上月末电表读数 本月末电表读数 单价 电费
220千瓦·时 310千瓦·时 元/(千瓦·时) 46.8元
试求出这张缴费单中的单价。
6.黄老师买了一本故事书和一支钢笔正好用去45.2元。其中一本故事书的价钱是一支钢笔的3倍。这本故事书和这支钢笔的价格各是多少元?(用方程解答)
7.甲、乙两地区4~9月份的平均气温如下表。
4 5 6 7 8 9
甲 9 16 18 23 24 20
乙 19 20 31 33 30 23
(1)根据表中的数据制成折线统计图。
(2)有一种植物的生长期为3个月,最适生长温度为15℃~23℃,这种植物适合在( )地区种植。
(3)孙文家住在乙地,6月份去甲地旅游,你认为他们应该做哪些准备?
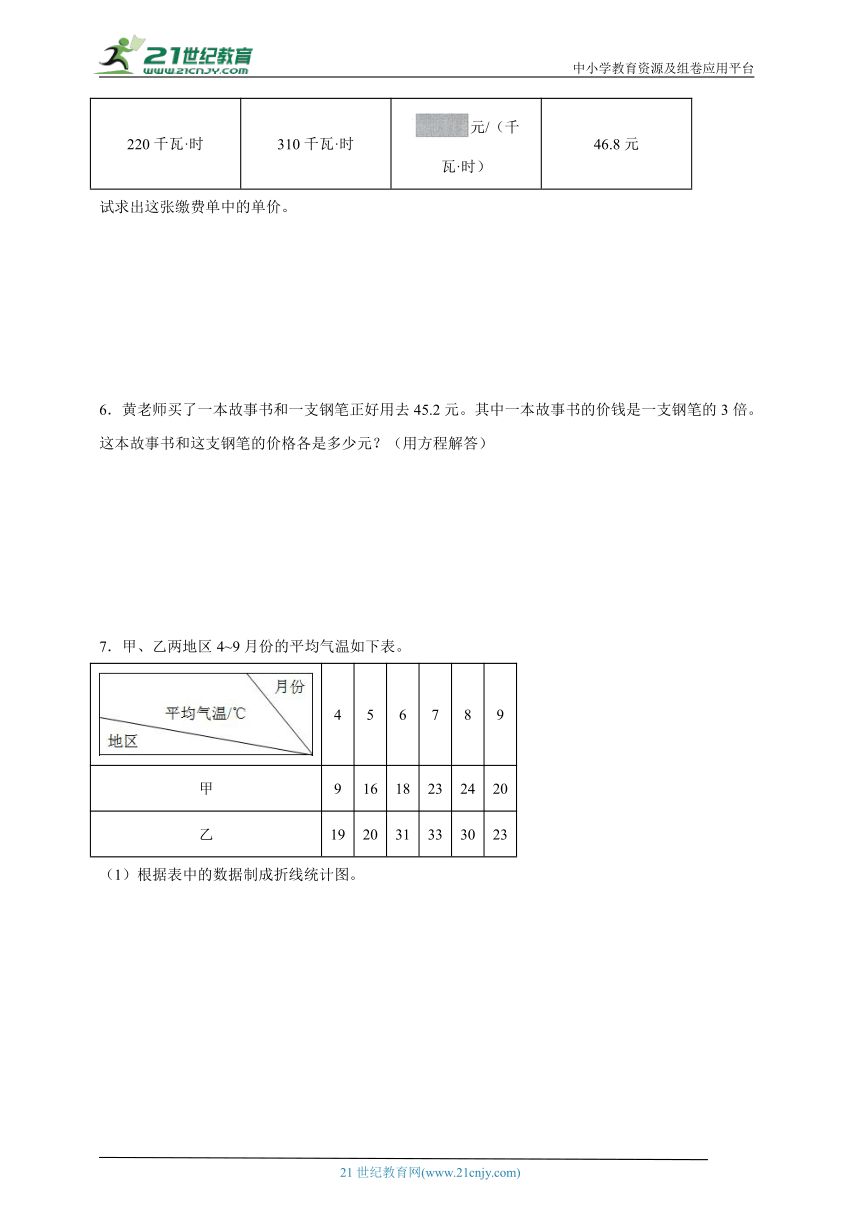
8.无人机因造型小巧、操作方便等特点被广泛应用。下表是A、B两架无人机在一次调试中的飞行时间和高度的统计表。请你根据统计表回答下面的问题。
时间/秒 高度/米 无人机 5 10 15 20 25 30
A 20 30 46 60 52 46
B 18 32 46 36 20 16
(1)请你根据统计表中的数据,补全折线统计图。
A、B两架无人机的飞行情况统计图
(2)从图上看,起飞后第( )秒,两架无人机的飞行高度是一样的;起飞后第( )秒,两架无人机的飞行高度相差最大。
(3)如果你需要购买一架无人机,你会选择无人机( ),理由是________________。
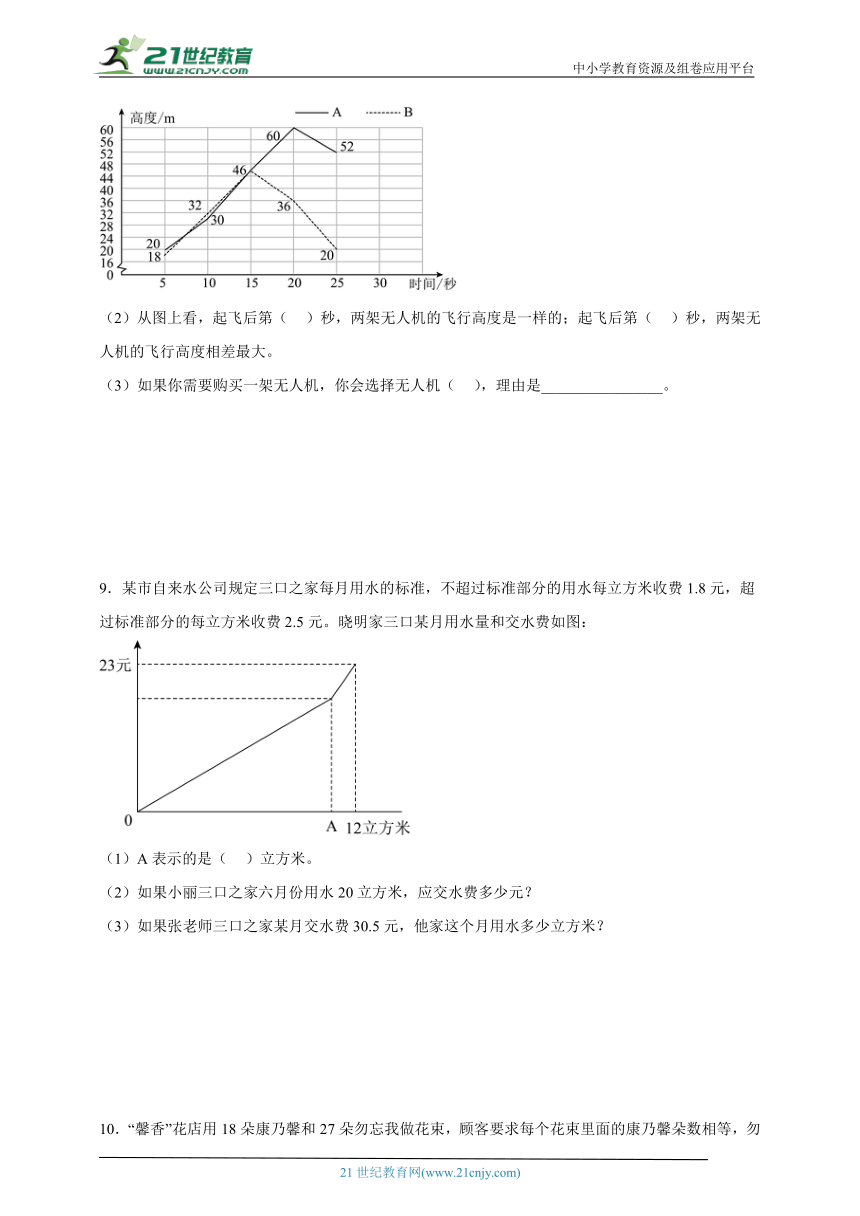
9.某市自来水公司规定三口之家每月用水的标准,不超过标准部分的用水每立方米收费1.8元,超过标准部分的每立方米收费2.5元。晓明家三口某月用水量和交水费如图:
(1)A表示的是( )立方米。
(2)如果小丽三口之家六月份用水20立方米,应交水费多少元?
(3)如果张老师三口之家某月交水费30.5元,他家这个月用水多少立方米?
10.“馨香”花店用18朵康乃馨和27朵勿忘我做花束,顾客要求每个花束里面的康乃馨朵数相等,勿忘我的朵数也相等,最多能做多少束?每个花束里有多少朵花?
11.用4~8这五个自然数连续不断地排成一个一百位数:456784567845678…,这个一百位数是6的倍数吗?写出你判断的理由。
12.李阿姨每工作2天休息一天,王阿姨每工作3天休息一天,如果5月20日她们同时在家休息,下次两人同时在家休息是几月几日?
13.明明、亮亮和丽丽是好朋友,有趣的是他们的年龄正好是三个连续自然数,且乘积是504。他们的年龄各是多少岁?
14.一个分数的分母比分子大36,约分后是。求这个分数。
15.果园里有橘子树120棵,苹果树50棵,梨树30棵。
(1)苹果树的棵数是橘子树的几分之几?
(2)梨树的棵数是三种果树总棵数的几分之几?
16.小红看一本故事书,第一天看了46页,第二天比第一天少看3页,刚好看完。第二天看了这本书的几分之几?
17.一个果园的总面积是公顷,其中梨占,苹果占,剩余的种其他果木。其他果木占果园总面积的几分之几?
18.一杯牛奶,喝去一半后,又给杯中加了升同样的牛奶,这时杯中的牛奶比原来少了升。这杯牛奶原来有多少升?
19.亚洲和北美洲的面积分别约占地球陆地面积的和。这两大洲的面积一共约占地球陆地面积的几分之几?
20.王老师用一根编织线编织了两个中国结。编织吉祥结用去了这根编织线的,比编织团锦结多用去这根编织线的。编织这两个中国结共用去这根编织线的几分之几?
21.县眼科医院来学校对学生进行了视力体检,上午进行体检的人数占全体学生的,下午进行体检的人数占全体学生的。还剩下全体学生的几分之几没有进行体检?
22.如图,学校圆形花坛的直径是12米;在花坛的周围有一条2米宽的小路。小路的面积是多少平方米?
23.下面正方形的边长是2厘米,在这个正方形内画一个最大的圆,圆的半径是多少厘米?直径呢?
24.丽丽骑自行车绕一个圆形花坛一周,前轮刚好滚动了100圈。已知自行车前轮外直径大约是66厘米,这个圆形花坛的周长大约是多少米?
25.红红家一扇窗户的形状是长方形和半圆形的组合。这扇窗户的周长和面积各是多少?
26.如下图,用铁丝把横截面直径是20厘米的2根圆木捆一圈,至少需要铁丝多少厘米?如果要捆4根圆木,至少需要铁丝多少厘米?(接头处忽略不计)
《【暑假应用题专项训练】第1-7单元-数学五年级下册苏教版》参考答案
1.4.3万元
【分析】求一个数的几倍是多少用乘法,比一个数多几就加几,设B轿车的售价是x万元,根据B轿车的售价×3+3.9=A轿车的售价,列出方程解答即可。
【详解】解:设B轿车的售价是x万元。
3x+3.9=16.8
3x+3.9-3.9=16.8-3.9
3x=12.9
3x÷3=12.9÷3
x=4.3
答:B轿车的售价是4.3万元。
2.11.95米
【分析】根据一架客机的机身总长比机高的4倍少8.9米,设机高为米,得出数量关系式:机身总长38.9米等于机高的4倍减去8.9米,列出方程,解方程得出机高。
【详解】解:设一架客机机高x米。
4x-8.9=38.9
4x=38.9+8.9
4x=47.8
x=47.8÷4
x=11.95
答:一架客机机高11.95米。
3.4.8厘米
【分析】设这张拼图的宽是x厘米,长是宽的3倍,则长是3x厘米;根据长方形周长公式:(长+宽)×2=周长,列方程:(3x+x)×2=38.4,解方程,即可解答。
【详解】解:设这张拼图的宽是x厘米,则长是3x厘米。
(3x+x)×2=38.4
4x×2=38.4
8x=38.4
8x÷8=38.4÷8
x=4.8
答:这张拼图的宽是4.8厘米。
4.95千米
【分析】设甲车每小时行x千米,根据“速度×时间=路程”可知,相遇时甲车行驶的路程是3.6x千米,乙车行了90×3.6千米,根据等量关系:“相遇时甲车行的路程-乙车行的路程=18千米”列方程解答即可。
【详解】解:设甲车每小时行x千米。
3.6x-90×3.6=18
3.6x-324=18
3.6x-324+324=18+324
3.6x=342
3.6x÷3.6=342÷3.6
x=95
答:甲车每小时行95千米。
5.0.52元/千瓦·时
【分析】设这张缴费单中的单价是x元/千瓦·时,先用本月末电表度数减去上月末电表读数,求出本月的用电量,根据“单价×数量=总价”求出本月的电费,又知道本月的电费是46.8元,据此等量关系列方程解答即可。
【详解】解:设这张缴费单中的单价是x元/千瓦·时。
(310-220)x=46.8
90x=46.8
90x÷90=46.8÷90
x=0.52
答:张缴费单中的单价是0.52元/千瓦·时。
6.故事书33.9元;钢笔11.3元
【分析】根据“一本故事书的价钱是一支钢笔的3倍”,可以设一支钢笔的价格是元,一本故事书的价格是3元;
根据“一本故事书和一支钢笔正好用去45.2元”,得出等量的关系:一支钢笔的价格+一本故事书的价格=一本故事书和一支钢笔的总价钱,据此列出方程,并求解。
【详解】解:设一支钢笔的价格是元,一本故事书的价格是3元。
+3=45.2
4=45.2
4÷4=45.2÷4
=11.3
11.3×3=33.9(元)
答:这本故事书的价格是33.9元,这支钢笔的价格是11.3元。
7.(1)图见详解
(2)甲
(3)见详解
【分析】(1)观察甲地和乙地在表格中的气温数据,并在统计图上找好相对应的横向和纵向坐标,并标记好点,并将每个点连接起来即可,据此作图。
(2)植物适种判断:甲地5-7月连续3个月均温均落在15-23℃区间内(16/18/23℃)
乙地仅4-5月达标,6月31℃超出适温范围根据气温情况,做出选择即可。
(3)旅行温差应对:6月乙地31℃→甲地23℃,温差8℃,需同时准备防晒(乙地高温)和保暖(甲地温差)。
【详解】
(1)
(2)甲地种植(5-7月温度验证:16℃(5月)→18℃(6月)→23℃(7月)均符合15-23℃要求;)
(3) 温差计算:31-23=8℃,6月乙地31℃→甲地23℃,温差8℃。
答:他们应该同时准备防晒(乙地高温)和保暖(甲地温差)。
8.(1)见详解
(2)15;25
(3)A;理由见详解
【分析】(1)在给定的折线统计图中,找到对应时间(横轴)和高度(纵轴)的交点,对于A无人机,在第30秒高度46米处准确描点,然后用实线顺次连接;对于B无人机,在第30秒高度16米处描点,用虚线顺次连接,补全折线统计图。
(2)对比A、B无人机每个时间点的高度,发现当时间为15秒时,A、B无人机高度都是46米,所以起飞后第15秒,两架无人机飞行高度一样;
高度相差最大时间:分别计算每个时间点A、B无人机的高度差,再比较,得出第几秒两架无人机的飞行高度相差最大。
(3)从飞行数据看,A无人机在20秒时达到最高高度60米,整体飞行过程中,除后期高度有所下降外,前期上升趋势明显,能达到较高飞行高度,且飞行高度在多数时间高于B无人机(如5秒、10秒、20秒、25秒、30秒 ),飞行性能(高度表现)更优,所以可选择A无人机 。
【详解】(1)统计图如下:
(2)20-18=2(米)
32-30=2(米)
46-46=0(米)
60-36=24(米)
52-20=32(米)
46-16=30(米)
0<2<24<30<32
从图上看,起飞后第15秒,两架无人机的飞行高度是一样的;起飞后第25秒,两架无人机的飞行高度相差最大。
(3)我会选择无人机A,理由是:因为A无人机的飞行高度高,飞行性能更优。(答案不唯一)
9.(1)10;
(2)43元;
(3)15立方米
【分析】(1)从图中可知,A表示标准用水量,用水量为12立方米收费23元,分成两段收费:
第一段,用水量为A立方米,单价1.8元;
第二段,用水量为(12-A)立方米,单价2.5元;
根据“单价×数量=总价”分别得出两段的费用,再相加,即是总费用23元,据此列出方程,并求出A的值。
(2)由上一问可知,A是10立方米。如果小丽三口之家六月份用水20立方米,20>10,分成两段收费:
第一段,用水量为10立方米,单价1.8元;
第二段,用水量为(20-10)立方米,单价2.5元;
根据“单价×数量=总价”分别得出两段的费用,再相加,即可求出应交的水费。
(3)如果张老师三口之家某月交水费30.5元,分成两段收费:
第一段,单价为1.8元,用水量为10立方米,根据“总价=单价×数量”,求出这一段的费用;
第二段,用水量超过10立方米以上的部分,单价2.5元,先用缴纳的水费减去第一段的费用,剩下的钱数就是第二段的费用,再根据“数量=总价÷单价”,即可求出超过10立方米以上的用水量;
最后把两段的用水量相加,就是张老师家这个月的总用水量。
【详解】(1)1.8A+(12-A)×2.5=23
解:1.8A+30-2.5A=23
30-2.5A+1.8A=23
30-(2.5A-1.8A)=23
30-0.7A=23
30-0.7A+0.7A=23+0.7A
23+0.7A=30
23+0.7A-23=30-23
0.7A=7
0.7A÷0.7=7÷0.7
A=10
A表示的是10立方米。
(2)1.8×10+2.5×(20-10)
=1.8×10+2.5×10
=18+25
=43(元)
答:应交水费43元。
(3)(30.5-1.8×10)÷2.5+10
=(30.5-18)÷2.5+10
=12.5÷2.5+10
=5+10
=15(立方米)
答:他家这个月用水15立方米。
【点睛】本题考查分段计费问题,弄清楚每段的临界点和每段的收费标准,然后根据单价、数量、总价之间的关系列式计算。
10.9束;5朵
【分析】求最多能做多少束,就是求18和27的最大公因数;两个数的公有质因数的连乘积就是这两个是的最大公因数;如果两个数为倍数关系,最大公因数为较小的那个数;如果两个数为互质数,最大公因数是1;据此求出18和27的最大公因数;再用康乃馨的朵数与勿忘我的朵数和除以最大公因数,即可解答。
【详解】18=2×3×3
27=3×3×3
18和27的最大公因数是3×3=9,最多能做9束。
(18+27)÷9
=45÷9
=5(朵)
答:最多能做9束,每个花束里有5朵花。
11.是6的倍数;理由见详解
【分析】个位上是0,2,4,6,8的数,都是2的倍数;一个数各个数位上的数的和是3的倍数,那么这个数就是3的倍数;由题意得,用4~8这五个自然数连续不断地排成一个一百位数:456784567845678…,即5个数为一组有规律地排列成一百位数。100÷5=20,即一共有20组这样的数排列成一百位数。所以这个数个位上的数是8,这个数是2的倍数。然后看这个数各个数位上的和是不是3的倍数。如果这个数各个数位上的和是3的倍数,那么这个数就是3的倍数。这个数同时是2的倍数和3的倍数,那么这个数就是6的倍数。反之它就不是6的倍数。
【详解】100÷5=20(组),所以这个一百位数的个位上的数是8,它是2的倍数。
4+5+6+7+8=9+6+7+8=15+7+8=22+8=30,30÷3=10,即这5个自然数的和是3的倍数,那么20组这样的自然数的和也是3的倍数,这个一百位数是3的倍数。所以这个一百位数是6的倍数。
答:这个一百位数是6的倍数,因为这个数的个位是8,是2的倍数且这个数各个数位上的数的和是3的倍数。
12.6月1日
【分析】根据题意,李阿姨每工作2天休息一天,即李阿姨每3天休息一天;王阿姨每工作3天休息一天,即王阿姨每4天休息一天;那么她们同时在家休息的间隔天数是3和4的公倍数;先求出3和4的最小公倍数,再加上上一次她们同时在家休息的日期,即可求出下次两人同时在家休息的日期。
【详解】2+1=3(天)
3+1=4(天)
3和4的最小公倍数是:3×4=12
即每12天两人同时在家休息。
5月20日+12天=6月1日
答:下次两人同时在家休息是6月1日。
13.7岁、8岁、9岁
【分析】将504分解质因数,再结合这三个数是连续的自然数进行解答即可。
【详解】504=2×2×2×3×3×7
2×2×2=8
3×3=9
则这三个连续自然数是7、8、9
答:他们的年龄分别是7岁、8岁和9岁。
14.
【分析】根据题意,一个分数的分母比分子大36,约分后是,约分后的分母比分子大7-3=4,36÷4=9,说明原来这个分数的分子、分母是同时除以9后得到,那么的分子、分母同时乘9,即可得到原来的分数。
【详解】36÷(7-3)
=36÷4
=9
=
答:这个分数是。
15.(1);
(2)
【分析】(1)分析题目,用苹果树的棵数除以橘子树的棵数即可求出苹果树的棵数是橘子树的几分之几;
(2)先用加法求出橘子树、苹果树、梨树一共有多少棵,再用梨树的棵数除以三种果树的总棵数即可解答。
【详解】(1)50÷120==
答:苹果树的棵数是橘子树的。
(2)30÷(120+50+30)
=30÷200
=
=
答:梨树的棵数是三种果树总棵数的。
16.
【分析】根据题意,用小红第一天看了的页数减去第二天比第一天少看的页数即可求出第二天看的页数,即46-3=43(页),总页数=第一天看的页数+第二天看的页数,第二天看书占全书的分率=第二天看的页数÷总页数,据此可得出答案。
【详解】小红第二天看了这本书的:
答:第二天看了这本书的。
17.
【分析】由题意可知,把果园的总面积看作单位“1”,已知梨占,苹果占,则剩余的用1减再减,即可得解。
【详解】
答:其他果木占果园总面积的。
18.升
【分析】根据题意,一杯牛奶,喝去一半后,又给杯中加了升同样的牛奶,这时杯中的牛奶比原来少了升,说明(+)升是原来牛奶的一半,所以原来牛奶有2个(+)升。
【详解】+
=+
=(升)
+=(升)
答:这杯牛奶原来有升。
19.
【分析】根据分数加法的意义,把亚洲和北美洲的面积分别约占地球陆地面积的和相加,即是这两大洲的面积一共约占地球陆地面积的几分之几。
【详解】
答:这两大洲的面积一共约占地球陆地面积的。
20.
【分析】将这根编织线看作单位“1”,用编织吉祥结的分率减去,求出编织团锦结用的分率,再将编织这两种中国结的分率相加,求出共用去这根编织线的几分之几。
【详解】
=
=
答:编织这两个中国结共用去这根编织线的。
21.
【分析】将全校学生看作单位“1”,用单位“1”减去上午体检的分率,再减去下午体检的分率,即可求出还剩下全体学生的几分之几没有进行体检。
【详解】
=
=
=
答:还剩下全体学生的没有进行体检。
22.87.92平方米
【分析】求小路的面积即求圆环的面积,内圆半径是12÷2=6(米),内圆半径加上小路的宽即外圆半径,根据环形面积公式S=π(-),代入公式计算即可。
【详解】12÷2=6(米)
6+2=8(米)
3.14×(-)
=3.14×(64-36)
=3.14×28
=87.92(平方米)
答:小路的面积是87.92平方米。
23.半径:1厘米;直径:2厘米
【分析】在一个正方形内画一个最大的圆,所画圆的直径应等于正方形的边长,圆的半径等于正方形边长的一半,据此解答。
【详解】在这个正方形内画一个最大的圆,圆的直径=正方形的边长=2厘米
圆的半径:2÷2=1(厘米)
答:在这个正方形内画一个最大的圆,圆的半径是1厘米,直径是2厘米。
24.207.24米
【分析】根据圆的周长=圆周率×直径,先求出自行车前轮滚动1圈的距离,再乘滚动圈数,即可求出自行车行驶距离,即花坛的周长,根据1米=100厘米,统一单位即可。
【详解】3.14×66×100
=207.24×100
=20724(厘米)
=207.24(米)
答:这个圆形花坛的周长大约是207.24米。
25.周长:8.14米;面积:4.57平方米
【分析】由图可知,半圆的直径等于长方形的长,这扇窗户的周长等于一个直径为2米的圆周长的一半加上长方形的1条长,再加上2条宽;这扇窗户的面积等于半圆的面积加上长方形的面积;根据圆的周长=πd,圆的面积=πr2,长方形的面积=长×宽,代入相应数值计算,据此解答。
【详解】周长:3.14×2÷2+1.5×2+2
=6.28÷2+3+2
=3.14+3+2
=8.14(米)
面积:3.14×(2÷2)2÷2+2×1.5
=3.14×11÷2+3
=3.14÷2+3
=1.57+3
=4.57(平方米)
答:这扇窗户的周长是8.14米,面积是4.57平方米。
26.102.8厘米;142.8厘米
【分析】根据题意,用铁丝把横截面直径是20厘米的2根圆木捆一圈,那么铁丝的长度相当于一个直径为20厘米的圆的周长加上2个直径的长度;
如果要捆4根圆木,铁丝的长度相当于一个直径为20厘米的圆的周长加上4个直径的长度;
根据圆的周长公式C=πd,代入数据计算求解。
【详解】3.14×20+20×2
=62.8+40
=102.8(厘米)
3.14×20+20×4
=62.8+80
=142.8(厘米)
答:用铁丝把横截面直径是20厘米的2根圆木捆一圈,至少需要铁丝102.8厘米;如果要捆4根圆木,至少需要铁丝142.8厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【暑假应用题专项训练】第1-7单元-数学五年级下册苏教版
1.A轿车的售价是16.8万元,比B轿车售价的3倍还多3.9万元。B轿车的售价是多少万元?
2.2023年5月28日,我国首架具有自主知识产权的干线客机圆满完成载客首飞。一架客机的机身总长38.9米,比机高的4倍少8.9米,一架客机机高多少米?(列方程解答)
3.小明买了一张长方形的游戏拼图,周长是38.4厘米。已知长是宽的3倍,这张拼图宽多少厘米?(列方程解答)
4.甲、乙两列火车同时从两地相对开出,经过3.6小时相遇,这时甲车比乙车多行18千米。已知乙车每小时行90千米,甲车每小时行多少千米?(列方程解答)
5.下面是一张不小心被弄脏的电费缴费单。
上月末电表读数 本月末电表读数 单价 电费
220千瓦·时 310千瓦·时 元/(千瓦·时) 46.8元
试求出这张缴费单中的单价。
6.黄老师买了一本故事书和一支钢笔正好用去45.2元。其中一本故事书的价钱是一支钢笔的3倍。这本故事书和这支钢笔的价格各是多少元?(用方程解答)
7.甲、乙两地区4~9月份的平均气温如下表。
4 5 6 7 8 9
甲 9 16 18 23 24 20
乙 19 20 31 33 30 23
(1)根据表中的数据制成折线统计图。
(2)有一种植物的生长期为3个月,最适生长温度为15℃~23℃,这种植物适合在( )地区种植。
(3)孙文家住在乙地,6月份去甲地旅游,你认为他们应该做哪些准备?
8.无人机因造型小巧、操作方便等特点被广泛应用。下表是A、B两架无人机在一次调试中的飞行时间和高度的统计表。请你根据统计表回答下面的问题。
时间/秒 高度/米 无人机 5 10 15 20 25 30
A 20 30 46 60 52 46
B 18 32 46 36 20 16
(1)请你根据统计表中的数据,补全折线统计图。
A、B两架无人机的飞行情况统计图
(2)从图上看,起飞后第( )秒,两架无人机的飞行高度是一样的;起飞后第( )秒,两架无人机的飞行高度相差最大。
(3)如果你需要购买一架无人机,你会选择无人机( ),理由是________________。
9.某市自来水公司规定三口之家每月用水的标准,不超过标准部分的用水每立方米收费1.8元,超过标准部分的每立方米收费2.5元。晓明家三口某月用水量和交水费如图:
(1)A表示的是( )立方米。
(2)如果小丽三口之家六月份用水20立方米,应交水费多少元?
(3)如果张老师三口之家某月交水费30.5元,他家这个月用水多少立方米?
10.“馨香”花店用18朵康乃馨和27朵勿忘我做花束,顾客要求每个花束里面的康乃馨朵数相等,勿忘我的朵数也相等,最多能做多少束?每个花束里有多少朵花?
11.用4~8这五个自然数连续不断地排成一个一百位数:456784567845678…,这个一百位数是6的倍数吗?写出你判断的理由。
12.李阿姨每工作2天休息一天,王阿姨每工作3天休息一天,如果5月20日她们同时在家休息,下次两人同时在家休息是几月几日?
13.明明、亮亮和丽丽是好朋友,有趣的是他们的年龄正好是三个连续自然数,且乘积是504。他们的年龄各是多少岁?
14.一个分数的分母比分子大36,约分后是。求这个分数。
15.果园里有橘子树120棵,苹果树50棵,梨树30棵。
(1)苹果树的棵数是橘子树的几分之几?
(2)梨树的棵数是三种果树总棵数的几分之几?
16.小红看一本故事书,第一天看了46页,第二天比第一天少看3页,刚好看完。第二天看了这本书的几分之几?
17.一个果园的总面积是公顷,其中梨占,苹果占,剩余的种其他果木。其他果木占果园总面积的几分之几?
18.一杯牛奶,喝去一半后,又给杯中加了升同样的牛奶,这时杯中的牛奶比原来少了升。这杯牛奶原来有多少升?
19.亚洲和北美洲的面积分别约占地球陆地面积的和。这两大洲的面积一共约占地球陆地面积的几分之几?
20.王老师用一根编织线编织了两个中国结。编织吉祥结用去了这根编织线的,比编织团锦结多用去这根编织线的。编织这两个中国结共用去这根编织线的几分之几?
21.县眼科医院来学校对学生进行了视力体检,上午进行体检的人数占全体学生的,下午进行体检的人数占全体学生的。还剩下全体学生的几分之几没有进行体检?
22.如图,学校圆形花坛的直径是12米;在花坛的周围有一条2米宽的小路。小路的面积是多少平方米?
23.下面正方形的边长是2厘米,在这个正方形内画一个最大的圆,圆的半径是多少厘米?直径呢?
24.丽丽骑自行车绕一个圆形花坛一周,前轮刚好滚动了100圈。已知自行车前轮外直径大约是66厘米,这个圆形花坛的周长大约是多少米?
25.红红家一扇窗户的形状是长方形和半圆形的组合。这扇窗户的周长和面积各是多少?
26.如下图,用铁丝把横截面直径是20厘米的2根圆木捆一圈,至少需要铁丝多少厘米?如果要捆4根圆木,至少需要铁丝多少厘米?(接头处忽略不计)
《【暑假应用题专项训练】第1-7单元-数学五年级下册苏教版》参考答案
1.4.3万元
【分析】求一个数的几倍是多少用乘法,比一个数多几就加几,设B轿车的售价是x万元,根据B轿车的售价×3+3.9=A轿车的售价,列出方程解答即可。
【详解】解:设B轿车的售价是x万元。
3x+3.9=16.8
3x+3.9-3.9=16.8-3.9
3x=12.9
3x÷3=12.9÷3
x=4.3
答:B轿车的售价是4.3万元。
2.11.95米
【分析】根据一架客机的机身总长比机高的4倍少8.9米,设机高为米,得出数量关系式:机身总长38.9米等于机高的4倍减去8.9米,列出方程,解方程得出机高。
【详解】解:设一架客机机高x米。
4x-8.9=38.9
4x=38.9+8.9
4x=47.8
x=47.8÷4
x=11.95
答:一架客机机高11.95米。
3.4.8厘米
【分析】设这张拼图的宽是x厘米,长是宽的3倍,则长是3x厘米;根据长方形周长公式:(长+宽)×2=周长,列方程:(3x+x)×2=38.4,解方程,即可解答。
【详解】解:设这张拼图的宽是x厘米,则长是3x厘米。
(3x+x)×2=38.4
4x×2=38.4
8x=38.4
8x÷8=38.4÷8
x=4.8
答:这张拼图的宽是4.8厘米。
4.95千米
【分析】设甲车每小时行x千米,根据“速度×时间=路程”可知,相遇时甲车行驶的路程是3.6x千米,乙车行了90×3.6千米,根据等量关系:“相遇时甲车行的路程-乙车行的路程=18千米”列方程解答即可。
【详解】解:设甲车每小时行x千米。
3.6x-90×3.6=18
3.6x-324=18
3.6x-324+324=18+324
3.6x=342
3.6x÷3.6=342÷3.6
x=95
答:甲车每小时行95千米。
5.0.52元/千瓦·时
【分析】设这张缴费单中的单价是x元/千瓦·时,先用本月末电表度数减去上月末电表读数,求出本月的用电量,根据“单价×数量=总价”求出本月的电费,又知道本月的电费是46.8元,据此等量关系列方程解答即可。
【详解】解:设这张缴费单中的单价是x元/千瓦·时。
(310-220)x=46.8
90x=46.8
90x÷90=46.8÷90
x=0.52
答:张缴费单中的单价是0.52元/千瓦·时。
6.故事书33.9元;钢笔11.3元
【分析】根据“一本故事书的价钱是一支钢笔的3倍”,可以设一支钢笔的价格是元,一本故事书的价格是3元;
根据“一本故事书和一支钢笔正好用去45.2元”,得出等量的关系:一支钢笔的价格+一本故事书的价格=一本故事书和一支钢笔的总价钱,据此列出方程,并求解。
【详解】解:设一支钢笔的价格是元,一本故事书的价格是3元。
+3=45.2
4=45.2
4÷4=45.2÷4
=11.3
11.3×3=33.9(元)
答:这本故事书的价格是33.9元,这支钢笔的价格是11.3元。
7.(1)图见详解
(2)甲
(3)见详解
【分析】(1)观察甲地和乙地在表格中的气温数据,并在统计图上找好相对应的横向和纵向坐标,并标记好点,并将每个点连接起来即可,据此作图。
(2)植物适种判断:甲地5-7月连续3个月均温均落在15-23℃区间内(16/18/23℃)
乙地仅4-5月达标,6月31℃超出适温范围根据气温情况,做出选择即可。
(3)旅行温差应对:6月乙地31℃→甲地23℃,温差8℃,需同时准备防晒(乙地高温)和保暖(甲地温差)。
【详解】
(1)
(2)甲地种植(5-7月温度验证:16℃(5月)→18℃(6月)→23℃(7月)均符合15-23℃要求;)
(3) 温差计算:31-23=8℃,6月乙地31℃→甲地23℃,温差8℃。
答:他们应该同时准备防晒(乙地高温)和保暖(甲地温差)。
8.(1)见详解
(2)15;25
(3)A;理由见详解
【分析】(1)在给定的折线统计图中,找到对应时间(横轴)和高度(纵轴)的交点,对于A无人机,在第30秒高度46米处准确描点,然后用实线顺次连接;对于B无人机,在第30秒高度16米处描点,用虚线顺次连接,补全折线统计图。
(2)对比A、B无人机每个时间点的高度,发现当时间为15秒时,A、B无人机高度都是46米,所以起飞后第15秒,两架无人机飞行高度一样;
高度相差最大时间:分别计算每个时间点A、B无人机的高度差,再比较,得出第几秒两架无人机的飞行高度相差最大。
(3)从飞行数据看,A无人机在20秒时达到最高高度60米,整体飞行过程中,除后期高度有所下降外,前期上升趋势明显,能达到较高飞行高度,且飞行高度在多数时间高于B无人机(如5秒、10秒、20秒、25秒、30秒 ),飞行性能(高度表现)更优,所以可选择A无人机 。
【详解】(1)统计图如下:
(2)20-18=2(米)
32-30=2(米)
46-46=0(米)
60-36=24(米)
52-20=32(米)
46-16=30(米)
0<2<24<30<32
从图上看,起飞后第15秒,两架无人机的飞行高度是一样的;起飞后第25秒,两架无人机的飞行高度相差最大。
(3)我会选择无人机A,理由是:因为A无人机的飞行高度高,飞行性能更优。(答案不唯一)
9.(1)10;
(2)43元;
(3)15立方米
【分析】(1)从图中可知,A表示标准用水量,用水量为12立方米收费23元,分成两段收费:
第一段,用水量为A立方米,单价1.8元;
第二段,用水量为(12-A)立方米,单价2.5元;
根据“单价×数量=总价”分别得出两段的费用,再相加,即是总费用23元,据此列出方程,并求出A的值。
(2)由上一问可知,A是10立方米。如果小丽三口之家六月份用水20立方米,20>10,分成两段收费:
第一段,用水量为10立方米,单价1.8元;
第二段,用水量为(20-10)立方米,单价2.5元;
根据“单价×数量=总价”分别得出两段的费用,再相加,即可求出应交的水费。
(3)如果张老师三口之家某月交水费30.5元,分成两段收费:
第一段,单价为1.8元,用水量为10立方米,根据“总价=单价×数量”,求出这一段的费用;
第二段,用水量超过10立方米以上的部分,单价2.5元,先用缴纳的水费减去第一段的费用,剩下的钱数就是第二段的费用,再根据“数量=总价÷单价”,即可求出超过10立方米以上的用水量;
最后把两段的用水量相加,就是张老师家这个月的总用水量。
【详解】(1)1.8A+(12-A)×2.5=23
解:1.8A+30-2.5A=23
30-2.5A+1.8A=23
30-(2.5A-1.8A)=23
30-0.7A=23
30-0.7A+0.7A=23+0.7A
23+0.7A=30
23+0.7A-23=30-23
0.7A=7
0.7A÷0.7=7÷0.7
A=10
A表示的是10立方米。
(2)1.8×10+2.5×(20-10)
=1.8×10+2.5×10
=18+25
=43(元)
答:应交水费43元。
(3)(30.5-1.8×10)÷2.5+10
=(30.5-18)÷2.5+10
=12.5÷2.5+10
=5+10
=15(立方米)
答:他家这个月用水15立方米。
【点睛】本题考查分段计费问题,弄清楚每段的临界点和每段的收费标准,然后根据单价、数量、总价之间的关系列式计算。
10.9束;5朵
【分析】求最多能做多少束,就是求18和27的最大公因数;两个数的公有质因数的连乘积就是这两个是的最大公因数;如果两个数为倍数关系,最大公因数为较小的那个数;如果两个数为互质数,最大公因数是1;据此求出18和27的最大公因数;再用康乃馨的朵数与勿忘我的朵数和除以最大公因数,即可解答。
【详解】18=2×3×3
27=3×3×3
18和27的最大公因数是3×3=9,最多能做9束。
(18+27)÷9
=45÷9
=5(朵)
答:最多能做9束,每个花束里有5朵花。
11.是6的倍数;理由见详解
【分析】个位上是0,2,4,6,8的数,都是2的倍数;一个数各个数位上的数的和是3的倍数,那么这个数就是3的倍数;由题意得,用4~8这五个自然数连续不断地排成一个一百位数:456784567845678…,即5个数为一组有规律地排列成一百位数。100÷5=20,即一共有20组这样的数排列成一百位数。所以这个数个位上的数是8,这个数是2的倍数。然后看这个数各个数位上的和是不是3的倍数。如果这个数各个数位上的和是3的倍数,那么这个数就是3的倍数。这个数同时是2的倍数和3的倍数,那么这个数就是6的倍数。反之它就不是6的倍数。
【详解】100÷5=20(组),所以这个一百位数的个位上的数是8,它是2的倍数。
4+5+6+7+8=9+6+7+8=15+7+8=22+8=30,30÷3=10,即这5个自然数的和是3的倍数,那么20组这样的自然数的和也是3的倍数,这个一百位数是3的倍数。所以这个一百位数是6的倍数。
答:这个一百位数是6的倍数,因为这个数的个位是8,是2的倍数且这个数各个数位上的数的和是3的倍数。
12.6月1日
【分析】根据题意,李阿姨每工作2天休息一天,即李阿姨每3天休息一天;王阿姨每工作3天休息一天,即王阿姨每4天休息一天;那么她们同时在家休息的间隔天数是3和4的公倍数;先求出3和4的最小公倍数,再加上上一次她们同时在家休息的日期,即可求出下次两人同时在家休息的日期。
【详解】2+1=3(天)
3+1=4(天)
3和4的最小公倍数是:3×4=12
即每12天两人同时在家休息。
5月20日+12天=6月1日
答:下次两人同时在家休息是6月1日。
13.7岁、8岁、9岁
【分析】将504分解质因数,再结合这三个数是连续的自然数进行解答即可。
【详解】504=2×2×2×3×3×7
2×2×2=8
3×3=9
则这三个连续自然数是7、8、9
答:他们的年龄分别是7岁、8岁和9岁。
14.
【分析】根据题意,一个分数的分母比分子大36,约分后是,约分后的分母比分子大7-3=4,36÷4=9,说明原来这个分数的分子、分母是同时除以9后得到,那么的分子、分母同时乘9,即可得到原来的分数。
【详解】36÷(7-3)
=36÷4
=9
=
答:这个分数是。
15.(1);
(2)
【分析】(1)分析题目,用苹果树的棵数除以橘子树的棵数即可求出苹果树的棵数是橘子树的几分之几;
(2)先用加法求出橘子树、苹果树、梨树一共有多少棵,再用梨树的棵数除以三种果树的总棵数即可解答。
【详解】(1)50÷120==
答:苹果树的棵数是橘子树的。
(2)30÷(120+50+30)
=30÷200
=
=
答:梨树的棵数是三种果树总棵数的。
16.
【分析】根据题意,用小红第一天看了的页数减去第二天比第一天少看的页数即可求出第二天看的页数,即46-3=43(页),总页数=第一天看的页数+第二天看的页数,第二天看书占全书的分率=第二天看的页数÷总页数,据此可得出答案。
【详解】小红第二天看了这本书的:
答:第二天看了这本书的。
17.
【分析】由题意可知,把果园的总面积看作单位“1”,已知梨占,苹果占,则剩余的用1减再减,即可得解。
【详解】
答:其他果木占果园总面积的。
18.升
【分析】根据题意,一杯牛奶,喝去一半后,又给杯中加了升同样的牛奶,这时杯中的牛奶比原来少了升,说明(+)升是原来牛奶的一半,所以原来牛奶有2个(+)升。
【详解】+
=+
=(升)
+=(升)
答:这杯牛奶原来有升。
19.
【分析】根据分数加法的意义,把亚洲和北美洲的面积分别约占地球陆地面积的和相加,即是这两大洲的面积一共约占地球陆地面积的几分之几。
【详解】
答:这两大洲的面积一共约占地球陆地面积的。
20.
【分析】将这根编织线看作单位“1”,用编织吉祥结的分率减去,求出编织团锦结用的分率,再将编织这两种中国结的分率相加,求出共用去这根编织线的几分之几。
【详解】
=
=
答:编织这两个中国结共用去这根编织线的。
21.
【分析】将全校学生看作单位“1”,用单位“1”减去上午体检的分率,再减去下午体检的分率,即可求出还剩下全体学生的几分之几没有进行体检。
【详解】
=
=
=
答:还剩下全体学生的没有进行体检。
22.87.92平方米
【分析】求小路的面积即求圆环的面积,内圆半径是12÷2=6(米),内圆半径加上小路的宽即外圆半径,根据环形面积公式S=π(-),代入公式计算即可。
【详解】12÷2=6(米)
6+2=8(米)
3.14×(-)
=3.14×(64-36)
=3.14×28
=87.92(平方米)
答:小路的面积是87.92平方米。
23.半径:1厘米;直径:2厘米
【分析】在一个正方形内画一个最大的圆,所画圆的直径应等于正方形的边长,圆的半径等于正方形边长的一半,据此解答。
【详解】在这个正方形内画一个最大的圆,圆的直径=正方形的边长=2厘米
圆的半径:2÷2=1(厘米)
答:在这个正方形内画一个最大的圆,圆的半径是1厘米,直径是2厘米。
24.207.24米
【分析】根据圆的周长=圆周率×直径,先求出自行车前轮滚动1圈的距离,再乘滚动圈数,即可求出自行车行驶距离,即花坛的周长,根据1米=100厘米,统一单位即可。
【详解】3.14×66×100
=207.24×100
=20724(厘米)
=207.24(米)
答:这个圆形花坛的周长大约是207.24米。
25.周长:8.14米;面积:4.57平方米
【分析】由图可知,半圆的直径等于长方形的长,这扇窗户的周长等于一个直径为2米的圆周长的一半加上长方形的1条长,再加上2条宽;这扇窗户的面积等于半圆的面积加上长方形的面积;根据圆的周长=πd,圆的面积=πr2,长方形的面积=长×宽,代入相应数值计算,据此解答。
【详解】周长:3.14×2÷2+1.5×2+2
=6.28÷2+3+2
=3.14+3+2
=8.14(米)
面积:3.14×(2÷2)2÷2+2×1.5
=3.14×11÷2+3
=3.14÷2+3
=1.57+3
=4.57(平方米)
答:这扇窗户的周长是8.14米,面积是4.57平方米。
26.102.8厘米;142.8厘米
【分析】根据题意,用铁丝把横截面直径是20厘米的2根圆木捆一圈,那么铁丝的长度相当于一个直径为20厘米的圆的周长加上2个直径的长度;
如果要捆4根圆木,铁丝的长度相当于一个直径为20厘米的圆的周长加上4个直径的长度;
根据圆的周长公式C=πd,代入数据计算求解。
【详解】3.14×20+20×2
=62.8+40
=102.8(厘米)
3.14×20+20×4
=62.8+80
=142.8(厘米)
答:用铁丝把横截面直径是20厘米的2根圆木捆一圈,至少需要铁丝102.8厘米;如果要捆4根圆木,至少需要铁丝142.8厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
