3.3 轴对称与坐标变化 学案(含答案) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 3.3 轴对称与坐标变化 学案(含答案) 2025-2026学年数学北师大版(2024)八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 98.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-04 00:00:00 | ||
图片预览

文档简介
3 轴对称与坐标变化 学案
班级 姓名 组别 总分
【学习目标】
1.经历轴对称变化与点的坐标的变化之间的关系的探索过程,发展数形结合意识,初步建立几何直观。
2.通过在直角坐标系中,以坐标轴为对称轴,能写出一个已知顶点坐标的多边形的对称图形点坐标过程,探究并知道对应顶点坐标之间的关系。
【学习过程】
任务一:轴对称与坐标变化
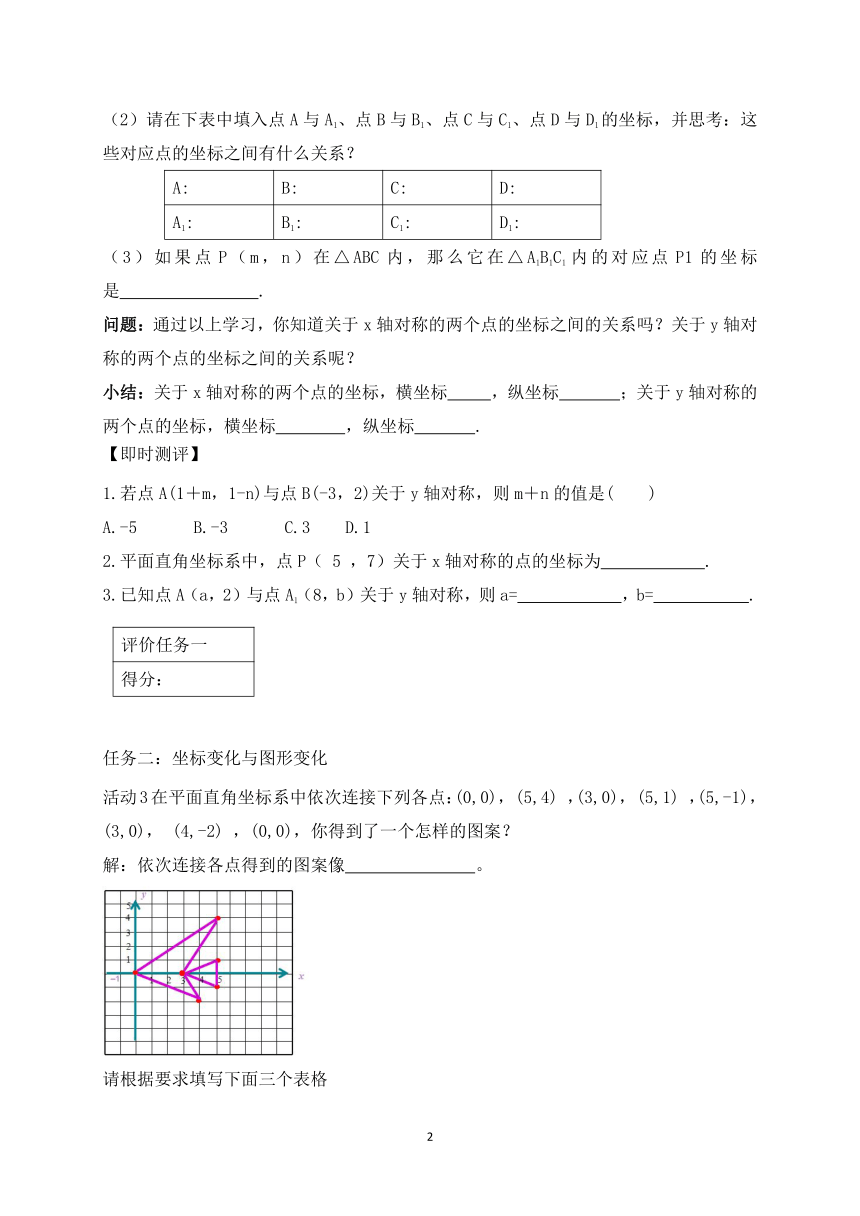
活动1 1.△ABC与△A1B1C1在如图所示的直角坐标系中,仔细观察,完成下列各题:
(1)△ABC与△A1B1C1有怎样的位置关系?
(2)请在下表中填入点A与A1、点B与B1、点C与C1的坐标,并思考:这些对应点的坐标之间有什么关系?
A: B: C:
A1: B1: C1:
(3)如果点P(m,n)在△ABC内,那么它在△A1B1C1内的对应点P1的坐标是 .
活动2如右图所示的平面直角坐标系中,第一、二象限内各有一面小旗.
(1)两面小旗之间有怎样的位置关系?
(2)请在下表中填入点A与A1、点B与B1、点C与C1、点D与D1的坐标,并思考:这些对应点的坐标之间有什么关系?
A: B: C: D:
A1: B1: C1: D1:
(3)如果点P(m,n)在△ABC内,那么它在△A1B1C1内的对应点P1的坐标是 .
问题:通过以上学习,你知道关于x轴对称的两个点的坐标之间的关系吗?关于y轴对称的两个点的坐标之间的关系呢?
小结:关于x轴对称的两个点的坐标,横坐标 ,纵坐标 ;关于y轴对称的两个点的坐标,横坐标 ,纵坐标 .
【即时测评】
1.若点A(1+m,1-n)与点B(-3,2)关于y轴对称,则m+n的值是( )
A.-5 B.-3 C.3 D.1
2.平面直角坐标系中,点P( 5 ,7)关于x轴对称的点的坐标为 .
3.已知点A(a,2)与点A1(8,b)关于y轴对称,则a= ,b= .
评价任务一
得分:
任务二:坐标变化与图形变化
活动3在平面直角坐标系中依次连接下列各点:(0,0), (5,4) ,(3,0), (5,1) ,(5,-1), (3,0), (4,-2) ,(0,0),你得到了一个怎样的图案?
解:依次连接各点得到的图案像 。
请根据要求填写下面三个表格
(1)将各坐标的纵坐标保持不变,横坐标都乘以-1 ,则图形怎么变化?
解:两个图形关于 对称
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(-x,y)
将各坐标的纵坐标都乘以-1,横坐标保持不变,则图形怎么变化?
解:两个图形关于 轴对称
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x,-y)
小结:
1.关于y轴对称的两个图形上点的坐标特征: .
2.关于x轴对称的两个图形上点的坐标特征: .
【即时测评】
4.如图,△ABC与△DFE关于y轴对称,已知A(-4,6),B(-6,2),E(2,1),则点D的坐标为( )
A.(-6,4) B.(4,6) C.(-2,1) D.(6,2)
5.已知A、B两点的坐标分别是(-2,3)和(2,3),则下面四个结论:①A、B关于x轴对称; ②A、B关于y轴对称;③A、B关于原点对称;④A、B之间的距离为4,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.点(-4,9)与点(4,9)的关系是( )
A.关于原点对称 B.关于x轴对称
C.关于y轴对称 D.不能构成对称关系
评价任务二
得分:
自我反思:
一节课的学习中,你收获了什么?
当堂训练:(要求:限时5分钟,独立完成后组内订正,成绩计入小组量化.)
1.点(4,3)与点(4,- 3)的关系是( )
A.关于原点对称 B.关于 x轴对称 C.关于 y轴对称 D.不能构成对称关系
2.点(m,- 1)和点(2,n)关于x轴对称, 则m n等于( )
A.- 2 B.2 C.1 D.- 1
3.一束光线从点A(3,3)出发,经过y轴上点C反射后经过点B(1,0),则光线从A点到B点经过的路线长是( )
A.4 B.5 C.6 D.7
4.已知点P(2a-3,3),点A(-1,3b+2),
(1)如果点P与点A关于x轴对称,那么a+b= ;
(2)如果点P与点A关于y轴对称,那么a+b= .
参考答案
即时测评:
1. D 2.(5,-7) 3. -8,2 4. B 5. B 6.C
当堂训练
1. B 2. B 3. B 4. (1)- (2)
1
班级 姓名 组别 总分
【学习目标】
1.经历轴对称变化与点的坐标的变化之间的关系的探索过程,发展数形结合意识,初步建立几何直观。
2.通过在直角坐标系中,以坐标轴为对称轴,能写出一个已知顶点坐标的多边形的对称图形点坐标过程,探究并知道对应顶点坐标之间的关系。
【学习过程】
任务一:轴对称与坐标变化
活动1 1.△ABC与△A1B1C1在如图所示的直角坐标系中,仔细观察,完成下列各题:
(1)△ABC与△A1B1C1有怎样的位置关系?
(2)请在下表中填入点A与A1、点B与B1、点C与C1的坐标,并思考:这些对应点的坐标之间有什么关系?
A: B: C:
A1: B1: C1:
(3)如果点P(m,n)在△ABC内,那么它在△A1B1C1内的对应点P1的坐标是 .
活动2如右图所示的平面直角坐标系中,第一、二象限内各有一面小旗.
(1)两面小旗之间有怎样的位置关系?
(2)请在下表中填入点A与A1、点B与B1、点C与C1、点D与D1的坐标,并思考:这些对应点的坐标之间有什么关系?
A: B: C: D:
A1: B1: C1: D1:
(3)如果点P(m,n)在△ABC内,那么它在△A1B1C1内的对应点P1的坐标是 .
问题:通过以上学习,你知道关于x轴对称的两个点的坐标之间的关系吗?关于y轴对称的两个点的坐标之间的关系呢?
小结:关于x轴对称的两个点的坐标,横坐标 ,纵坐标 ;关于y轴对称的两个点的坐标,横坐标 ,纵坐标 .
【即时测评】
1.若点A(1+m,1-n)与点B(-3,2)关于y轴对称,则m+n的值是( )
A.-5 B.-3 C.3 D.1
2.平面直角坐标系中,点P( 5 ,7)关于x轴对称的点的坐标为 .
3.已知点A(a,2)与点A1(8,b)关于y轴对称,则a= ,b= .
评价任务一
得分:
任务二:坐标变化与图形变化
活动3在平面直角坐标系中依次连接下列各点:(0,0), (5,4) ,(3,0), (5,1) ,(5,-1), (3,0), (4,-2) ,(0,0),你得到了一个怎样的图案?
解:依次连接各点得到的图案像 。
请根据要求填写下面三个表格
(1)将各坐标的纵坐标保持不变,横坐标都乘以-1 ,则图形怎么变化?
解:两个图形关于 对称
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(-x,y)
将各坐标的纵坐标都乘以-1,横坐标保持不变,则图形怎么变化?
解:两个图形关于 轴对称
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x,-y)
小结:
1.关于y轴对称的两个图形上点的坐标特征: .
2.关于x轴对称的两个图形上点的坐标特征: .
【即时测评】
4.如图,△ABC与△DFE关于y轴对称,已知A(-4,6),B(-6,2),E(2,1),则点D的坐标为( )
A.(-6,4) B.(4,6) C.(-2,1) D.(6,2)
5.已知A、B两点的坐标分别是(-2,3)和(2,3),则下面四个结论:①A、B关于x轴对称; ②A、B关于y轴对称;③A、B关于原点对称;④A、B之间的距离为4,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.点(-4,9)与点(4,9)的关系是( )
A.关于原点对称 B.关于x轴对称
C.关于y轴对称 D.不能构成对称关系
评价任务二
得分:
自我反思:
一节课的学习中,你收获了什么?
当堂训练:(要求:限时5分钟,独立完成后组内订正,成绩计入小组量化.)
1.点(4,3)与点(4,- 3)的关系是( )
A.关于原点对称 B.关于 x轴对称 C.关于 y轴对称 D.不能构成对称关系
2.点(m,- 1)和点(2,n)关于x轴对称, 则m n等于( )
A.- 2 B.2 C.1 D.- 1
3.一束光线从点A(3,3)出发,经过y轴上点C反射后经过点B(1,0),则光线从A点到B点经过的路线长是( )
A.4 B.5 C.6 D.7
4.已知点P(2a-3,3),点A(-1,3b+2),
(1)如果点P与点A关于x轴对称,那么a+b= ;
(2)如果点P与点A关于y轴对称,那么a+b= .
参考答案
即时测评:
1. D 2.(5,-7) 3. -8,2 4. B 5. B 6.C
当堂训练
1. B 2. B 3. B 4. (1)- (2)
1
同课章节目录
