5.4 第1课时 二元一次方程与一次函数的关系 学案(含答案) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 5.4 第1课时 二元一次方程与一次函数的关系 学案(含答案) 2025-2026学年数学北师大版(2024)八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 121.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-04 00:00:00 | ||
图片预览

文档简介
4 二元一次方程与一次函数
第1课时 二元一次方程与一次函数的关系 学案
班级 姓名 组别 总分
【学习目标】
1.通过观看函数图像,能描述方程和图像之间的对应关系, 感受它们的密切联系,发展抽象能力.
2.通过动手操作,结合具体实例理解二元一次方程与一次函数的关系,,能用其性质解决简单的数学问题,发展归纳能力及应用意识.
3.通过自主学习,体会数形结合研究数学问题的思想,,发展自主学习及动手能力.
【学习过程】
任务一:二元一次方程与一次函数的关系
问题1:方程 x + y = 5 的解有多少个 写出其中的几个.
问题2:等式 x + y = 5 还可以看成一个一次函数,把它变成 y = kx + b 的形式是___________.
问题3:画出 y = -x + 5 的图象.
追问①:以方程 x + y = 5 的解为坐标的点都在一次函数y = -x + 5 的图象上吗?
追问②:在一次函数 y = -x + 5的图象上任取一点,点的坐标适合方程 x + y = 5 吗?
追问③:以方程 x + y = 5 的解为坐标的所有点组成的图象与一次函数 y = -x + 5 的图象相同吗?
【方法归纳】二元一次方程与一次函数的关系:
【即时测评】
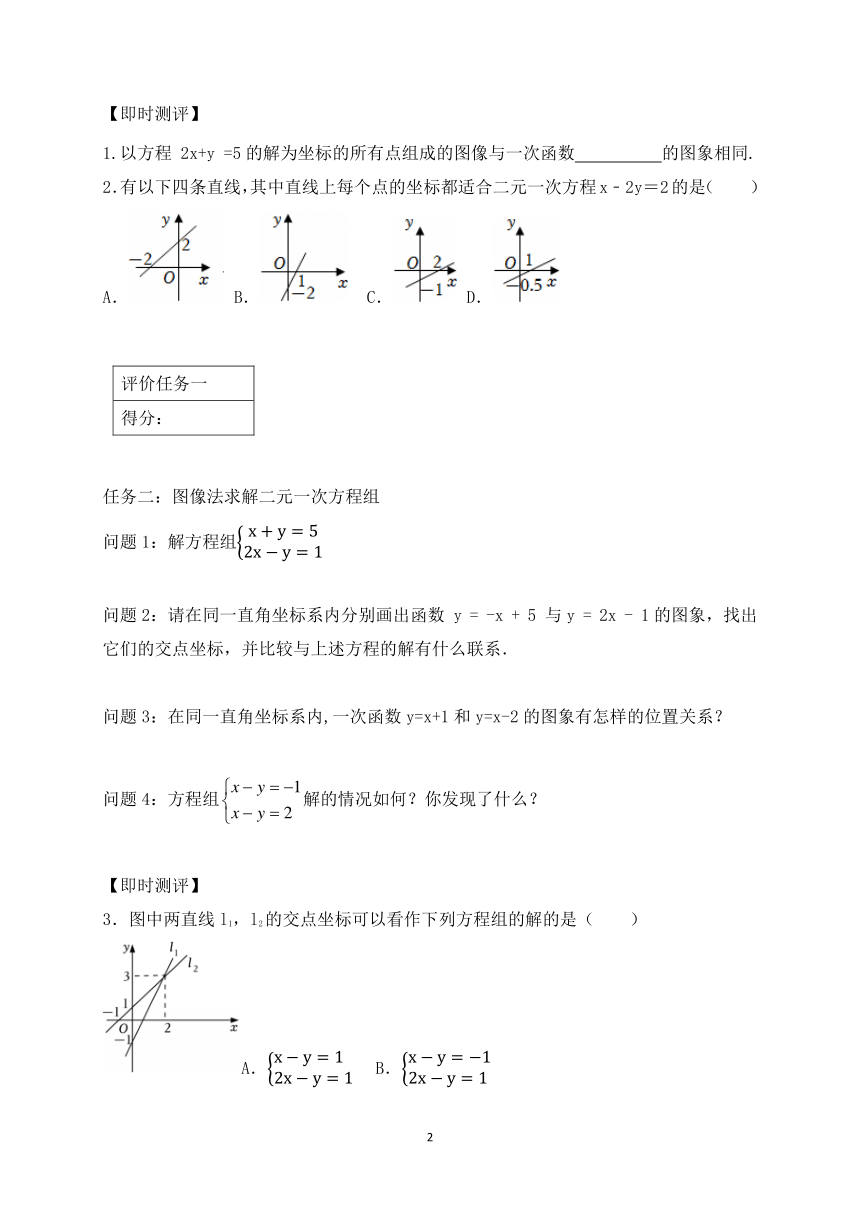
1.以方程 2x+y =5的解为坐标的所有点组成的图像与一次函数 的图象相同.
2.有以下四条直线,其中直线上每个点的坐标都适合二元一次方程x﹣2y=2的是( )
A. B. C. D.
评价任务一
得分:
任务二:图像法求解二元一次方程组
问题1:解方程组
问题2:请在同一直角坐标系内分别画出函数 y = -x + 5 与y = 2x - 1的图象,找出它们的交点坐标,并比较与上述方程的解有什么联系.
问题3:在同一直角坐标系内,一次函数y=x+1和y=x-2的图象有怎样的位置关系?
问题4:方程组解的情况如何?你发现了什么?
【即时测评】
3.图中两直线l1,l2的交点坐标可以看作下列方程组的解的是( )
A. B.
C. D.
4.用图象法解二元一次方程组.
评价任务二
得分:
自我反思:
一节课的学习中,你收获了什么?
当堂训练:(要求:限时5分钟,独立完成后组内订正,成绩计入小组量化.)
1.若方程组没有解,则一次函数y=2﹣x与yx的图象必定( )
A.重合 B.平行 C.相交 D.无法确定
2.已知方程组的解是,则一次函数y=ax+b与y=kx的交点P的坐标是 .
3.已知方程组的解为,则一次函数y=﹣x+1和y=2x﹣2的图象的交点坐标为 .
4.已知:一次函数y=3x﹣5与y=2x+b的图象的交点的坐标为P(1,﹣2).
求:方程组的解和b的值.
参考答案
即时测评:
1. y =-2x+5
2.C
3.B
4.解:如图所示:
两函数图相交于点(3,﹣2),
因此二元一次方程组的解为.
当堂训练
1. B
2.(1,3)
3.(1,0)
4.解:∵一次函与y=3x﹣5与y=2x+的图象的交点的坐标为P(1,﹣2)
∴方程组的解是,
将点P(1,﹣2)的坐标代y=2x+b,得b=﹣4.
1
第1课时 二元一次方程与一次函数的关系 学案
班级 姓名 组别 总分
【学习目标】
1.通过观看函数图像,能描述方程和图像之间的对应关系, 感受它们的密切联系,发展抽象能力.
2.通过动手操作,结合具体实例理解二元一次方程与一次函数的关系,,能用其性质解决简单的数学问题,发展归纳能力及应用意识.
3.通过自主学习,体会数形结合研究数学问题的思想,,发展自主学习及动手能力.
【学习过程】
任务一:二元一次方程与一次函数的关系
问题1:方程 x + y = 5 的解有多少个 写出其中的几个.
问题2:等式 x + y = 5 还可以看成一个一次函数,把它变成 y = kx + b 的形式是___________.
问题3:画出 y = -x + 5 的图象.
追问①:以方程 x + y = 5 的解为坐标的点都在一次函数y = -x + 5 的图象上吗?
追问②:在一次函数 y = -x + 5的图象上任取一点,点的坐标适合方程 x + y = 5 吗?
追问③:以方程 x + y = 5 的解为坐标的所有点组成的图象与一次函数 y = -x + 5 的图象相同吗?
【方法归纳】二元一次方程与一次函数的关系:
【即时测评】
1.以方程 2x+y =5的解为坐标的所有点组成的图像与一次函数 的图象相同.
2.有以下四条直线,其中直线上每个点的坐标都适合二元一次方程x﹣2y=2的是( )
A. B. C. D.
评价任务一
得分:
任务二:图像法求解二元一次方程组
问题1:解方程组
问题2:请在同一直角坐标系内分别画出函数 y = -x + 5 与y = 2x - 1的图象,找出它们的交点坐标,并比较与上述方程的解有什么联系.
问题3:在同一直角坐标系内,一次函数y=x+1和y=x-2的图象有怎样的位置关系?
问题4:方程组解的情况如何?你发现了什么?
【即时测评】
3.图中两直线l1,l2的交点坐标可以看作下列方程组的解的是( )
A. B.
C. D.
4.用图象法解二元一次方程组.
评价任务二
得分:
自我反思:
一节课的学习中,你收获了什么?
当堂训练:(要求:限时5分钟,独立完成后组内订正,成绩计入小组量化.)
1.若方程组没有解,则一次函数y=2﹣x与yx的图象必定( )
A.重合 B.平行 C.相交 D.无法确定
2.已知方程组的解是,则一次函数y=ax+b与y=kx的交点P的坐标是 .
3.已知方程组的解为,则一次函数y=﹣x+1和y=2x﹣2的图象的交点坐标为 .
4.已知:一次函数y=3x﹣5与y=2x+b的图象的交点的坐标为P(1,﹣2).
求:方程组的解和b的值.
参考答案
即时测评:
1. y =-2x+5
2.C
3.B
4.解:如图所示:
两函数图相交于点(3,﹣2),
因此二元一次方程组的解为.
当堂训练
1. B
2.(1,3)
3.(1,0)
4.解:∵一次函与y=3x﹣5与y=2x+的图象的交点的坐标为P(1,﹣2)
∴方程组的解是,
将点P(1,﹣2)的坐标代y=2x+b,得b=﹣4.
1
同课章节目录
