3.3函数的应用(一)(教学课件)——高中数学人教B版(2019)必修第一册(共29张PPT)
文档属性
| 名称 | 3.3函数的应用(一)(教学课件)——高中数学人教B版(2019)必修第一册(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 33.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-04 22:51:49 | ||
图片预览








文档简介
(共29张PPT)
3.3函数的应用(一)
人教B版(2019)必修第一册
第二章 等式与不等式
学习目标
理解一次函数模型
01
理解二次函数模型
02
理解分段函数模型
03
探索新知
因为函数可以描述一个量依赖于另外一个量变化而变化的情况,函数的应用不仅体现在用函数解决数学问题,还体现在用函数解决实际问题,所以函数的知识在实际生活中有着广泛的应用.本节课我们将利用给定的函数模型或建立函数模型解决实际问题,并对给定的函数模型进行简单的分析评价.下面我们通过例子来说明.
典型例题
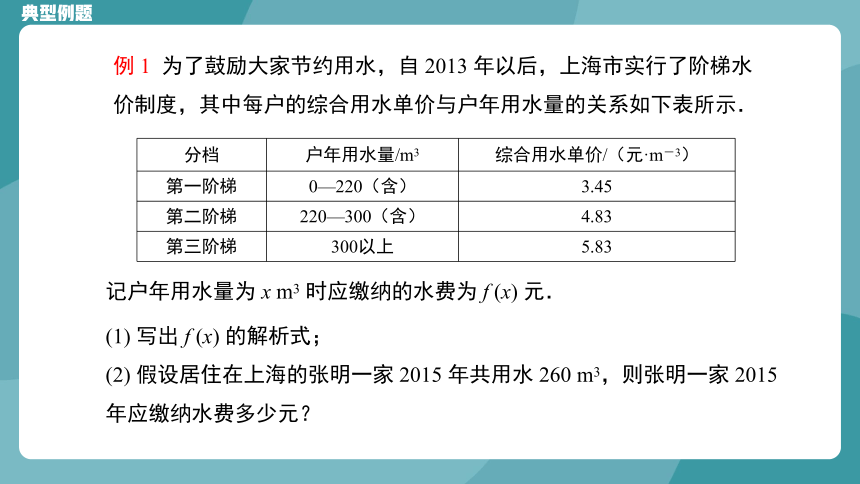
例 1 为了鼓励大家节约用水,自 2013 年以后,上海市实行了阶梯水价制度,其中每户的综合用水单价与户年用水量的关系如下表所示.
(1) 写出 f (x) 的解析式;
(2) 假设居住在上海的张明一家 2015 年共用水 260 m3,则张明一家 2015年应缴纳水费多少元?
记户年用水量为 x m3 时应缴纳的水费为 f (x) 元.
分档 户年用水量/m3 综合用水单价/(元·m-3)
第一阶梯 0—220(含) 3.45
第二阶梯 220—300(含) 4.83
第三阶梯 300以上 5.83
典型例题
例 1 (1) 写出 f (x) 的解析式;
典型例题
例 1 (2) 假设居住在上海的张明一家 2015 年共用水 260 m3,则张明一家 2015 年应缴纳水费多少元?
解:因为 220<260≤300,所以
f (260)=4.83×260-303.6=952.2,
因此张明一家 2015 年应缴纳水费 952.2 元.
由例 1 可知,可以用分段函数来描述生活中的阶梯水价、阶梯电价等内容
典型例题
例 2 城镇化是国家现代化的重要指标,据有关资料显示,1978—2013 年,我国城镇常住人口从 1.7 亿增加到 7.3 亿,假设每一年城镇常住人口的增加量都相等,记 1978 年后第 t (限定 t<40 ) 年的城镇常住人口为 f (t) 亿. 写出 f (t) 的解析式,并由此估算出我国 2017 年的城镇常住人口数.
典型例题
解:因为每一年城镇常住人口的增加量都相等,所以 f (t) 是一次函数,设 f (t)=kt+b,其中 k,b 是常数
注意到 2013 年是 1978 年后的第 2013-1978=35 年,因此
解得 k=0.16,b=1.7.因此
f (t)=0.16t+1.7,t∈N 且 t<40.
又因为 2017 年是 1978 年后的第 2017-1978=39 年,而且
f (39)=0.16×39+1.7=7.94,
所以由此可估算出我国 2017 年的城镇常住人口为 7.94 亿.
典型例题
例 3 某农家旅游公司有客房 160 间,每间房单价为 200 元时,每天都客满.已知每间房单价每提高 20 元,则客房出租数就会减少 10间.若不考虑其他因素,旅游公司把每间房单价提到多少时,每天客房的租金总收入最高?
典型例题
分析:可以通过试算来理解题意,如下表所示.
提价/元 每间房单价/元 客房出租数 租金总收入/元
0 200 160 32 000
20 220 150 33 000
40 240 140 33 600
60 260 130 33 800
80 280 120 33 600
100 300 110 33 000
120 320 100 32 000
典型例题
解:设每间房单价提高 x 个 20 元时,每天客房的租金总收入为 y 元.
因为此时每间房单价为 200+20x 元,而客房出租数将减少 10x 间,即为 160-10x 间,因此
y=(200+20x)(160-10x)
=200(10+x)(16-x)
=200(-x2+6x+160)
=200[-(x-3)2+169]
=-200(x-3)2+33 800.
从而可知,当 x=3 时,y 的最大值为 33 800.
因此每间房单价提到 200+20×3=260 元时,每天客房的租金总收入最高.
典型例题
例 4 某单位计划用围墙围出一块矩形场地,现有材料可筑墙的总长度为 l,如果要使围墙围出的场地面积最大,则矩形的长、宽各等于多少?
解:设矩形的长为 x 时,场地的面积为 S.
因为矩形的周长要为 l,所以矩形的宽为 ,由
可解得 .
典型例题
例 4 某单位计划用围墙围出一块矩形场地,现有材料可筑墙的总长度为 l,如果要使围墙围出的场地面积最大,则矩形的长、宽各等于多少?
又因为
此时矩形的宽为
即所围矩形是长、宽都为 的正方形时,场地面积最大.
所以当 时,S 的最大值为 .
探索新知
想一想
你能用均值不等式求得 S 的最大值吗?
设矩形的长为 x,宽为 y,
则 x>0,y>0,x+y= ,
故有 =x+y≥ ,即 S=xy≤ ,
当且仅当 x=y= 时,
S 的最大值为 .
典型例题
例 5 已知某产品的总成本 C 与年产量 Q 之间的关系为 C=aQ2+3000,且当年产量是 100 时,总成本是 6000.设该产品年产量为 Q 时的平均成本为 f (Q).
(1) 求 f (Q) 的解析式;
典型例题
例 5 已知某产品的总成本 C 与年产量 Q 之间的关系为 C=aQ2+3000,且当年产量是 100 时,总成本是 6000.设该产品年产量为 Q 时的平均成本为 f (Q).
(2) 求年产量为多少时,平均成本最小,并求最小值.
当堂检测
当堂检测
C
当堂检测
D
当堂检测
B
当堂检测
B
当堂检测
当堂检测
当堂检测
14.59
9
当堂检测
当堂检测
当堂检测
本节课学习了哪些知识点呢?
1.一次函数模型;
2.二次函数模型;
3.分段函数模型.
感谢观看
祝同学新学期新气象
3.3函数的应用(一)
人教B版(2019)必修第一册
第二章 等式与不等式
学习目标
理解一次函数模型
01
理解二次函数模型
02
理解分段函数模型
03
探索新知
因为函数可以描述一个量依赖于另外一个量变化而变化的情况,函数的应用不仅体现在用函数解决数学问题,还体现在用函数解决实际问题,所以函数的知识在实际生活中有着广泛的应用.本节课我们将利用给定的函数模型或建立函数模型解决实际问题,并对给定的函数模型进行简单的分析评价.下面我们通过例子来说明.
典型例题
例 1 为了鼓励大家节约用水,自 2013 年以后,上海市实行了阶梯水价制度,其中每户的综合用水单价与户年用水量的关系如下表所示.
(1) 写出 f (x) 的解析式;
(2) 假设居住在上海的张明一家 2015 年共用水 260 m3,则张明一家 2015年应缴纳水费多少元?
记户年用水量为 x m3 时应缴纳的水费为 f (x) 元.
分档 户年用水量/m3 综合用水单价/(元·m-3)
第一阶梯 0—220(含) 3.45
第二阶梯 220—300(含) 4.83
第三阶梯 300以上 5.83
典型例题
例 1 (1) 写出 f (x) 的解析式;
典型例题
例 1 (2) 假设居住在上海的张明一家 2015 年共用水 260 m3,则张明一家 2015 年应缴纳水费多少元?
解:因为 220<260≤300,所以
f (260)=4.83×260-303.6=952.2,
因此张明一家 2015 年应缴纳水费 952.2 元.
由例 1 可知,可以用分段函数来描述生活中的阶梯水价、阶梯电价等内容
典型例题
例 2 城镇化是国家现代化的重要指标,据有关资料显示,1978—2013 年,我国城镇常住人口从 1.7 亿增加到 7.3 亿,假设每一年城镇常住人口的增加量都相等,记 1978 年后第 t (限定 t<40 ) 年的城镇常住人口为 f (t) 亿. 写出 f (t) 的解析式,并由此估算出我国 2017 年的城镇常住人口数.
典型例题
解:因为每一年城镇常住人口的增加量都相等,所以 f (t) 是一次函数,设 f (t)=kt+b,其中 k,b 是常数
注意到 2013 年是 1978 年后的第 2013-1978=35 年,因此
解得 k=0.16,b=1.7.因此
f (t)=0.16t+1.7,t∈N 且 t<40.
又因为 2017 年是 1978 年后的第 2017-1978=39 年,而且
f (39)=0.16×39+1.7=7.94,
所以由此可估算出我国 2017 年的城镇常住人口为 7.94 亿.
典型例题
例 3 某农家旅游公司有客房 160 间,每间房单价为 200 元时,每天都客满.已知每间房单价每提高 20 元,则客房出租数就会减少 10间.若不考虑其他因素,旅游公司把每间房单价提到多少时,每天客房的租金总收入最高?
典型例题
分析:可以通过试算来理解题意,如下表所示.
提价/元 每间房单价/元 客房出租数 租金总收入/元
0 200 160 32 000
20 220 150 33 000
40 240 140 33 600
60 260 130 33 800
80 280 120 33 600
100 300 110 33 000
120 320 100 32 000
典型例题
解:设每间房单价提高 x 个 20 元时,每天客房的租金总收入为 y 元.
因为此时每间房单价为 200+20x 元,而客房出租数将减少 10x 间,即为 160-10x 间,因此
y=(200+20x)(160-10x)
=200(10+x)(16-x)
=200(-x2+6x+160)
=200[-(x-3)2+169]
=-200(x-3)2+33 800.
从而可知,当 x=3 时,y 的最大值为 33 800.
因此每间房单价提到 200+20×3=260 元时,每天客房的租金总收入最高.
典型例题
例 4 某单位计划用围墙围出一块矩形场地,现有材料可筑墙的总长度为 l,如果要使围墙围出的场地面积最大,则矩形的长、宽各等于多少?
解:设矩形的长为 x 时,场地的面积为 S.
因为矩形的周长要为 l,所以矩形的宽为 ,由
可解得 .
典型例题
例 4 某单位计划用围墙围出一块矩形场地,现有材料可筑墙的总长度为 l,如果要使围墙围出的场地面积最大,则矩形的长、宽各等于多少?
又因为
此时矩形的宽为
即所围矩形是长、宽都为 的正方形时,场地面积最大.
所以当 时,S 的最大值为 .
探索新知
想一想
你能用均值不等式求得 S 的最大值吗?
设矩形的长为 x,宽为 y,
则 x>0,y>0,x+y= ,
故有 =x+y≥ ,即 S=xy≤ ,
当且仅当 x=y= 时,
S 的最大值为 .
典型例题
例 5 已知某产品的总成本 C 与年产量 Q 之间的关系为 C=aQ2+3000,且当年产量是 100 时,总成本是 6000.设该产品年产量为 Q 时的平均成本为 f (Q).
(1) 求 f (Q) 的解析式;
典型例题
例 5 已知某产品的总成本 C 与年产量 Q 之间的关系为 C=aQ2+3000,且当年产量是 100 时,总成本是 6000.设该产品年产量为 Q 时的平均成本为 f (Q).
(2) 求年产量为多少时,平均成本最小,并求最小值.
当堂检测
当堂检测
C
当堂检测
D
当堂检测
B
当堂检测
B
当堂检测
当堂检测
当堂检测
14.59
9
当堂检测
当堂检测
当堂检测
本节课学习了哪些知识点呢?
1.一次函数模型;
2.二次函数模型;
3.分段函数模型.
感谢观看
祝同学新学期新气象
