北师大版数学七年级上册-单元培优第1章 丰富的图形世界(原卷版+详解)
文档属性
| 名称 | 北师大版数学七年级上册-单元培优第1章 丰富的图形世界(原卷版+详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-04 18:24:00 | ||
图片预览

文档简介
第1章 丰富的图形世界(单元培优卷 北师大版)
考试时间:120分钟,满分:120分
选择题:共10题,每题3分,共30分。
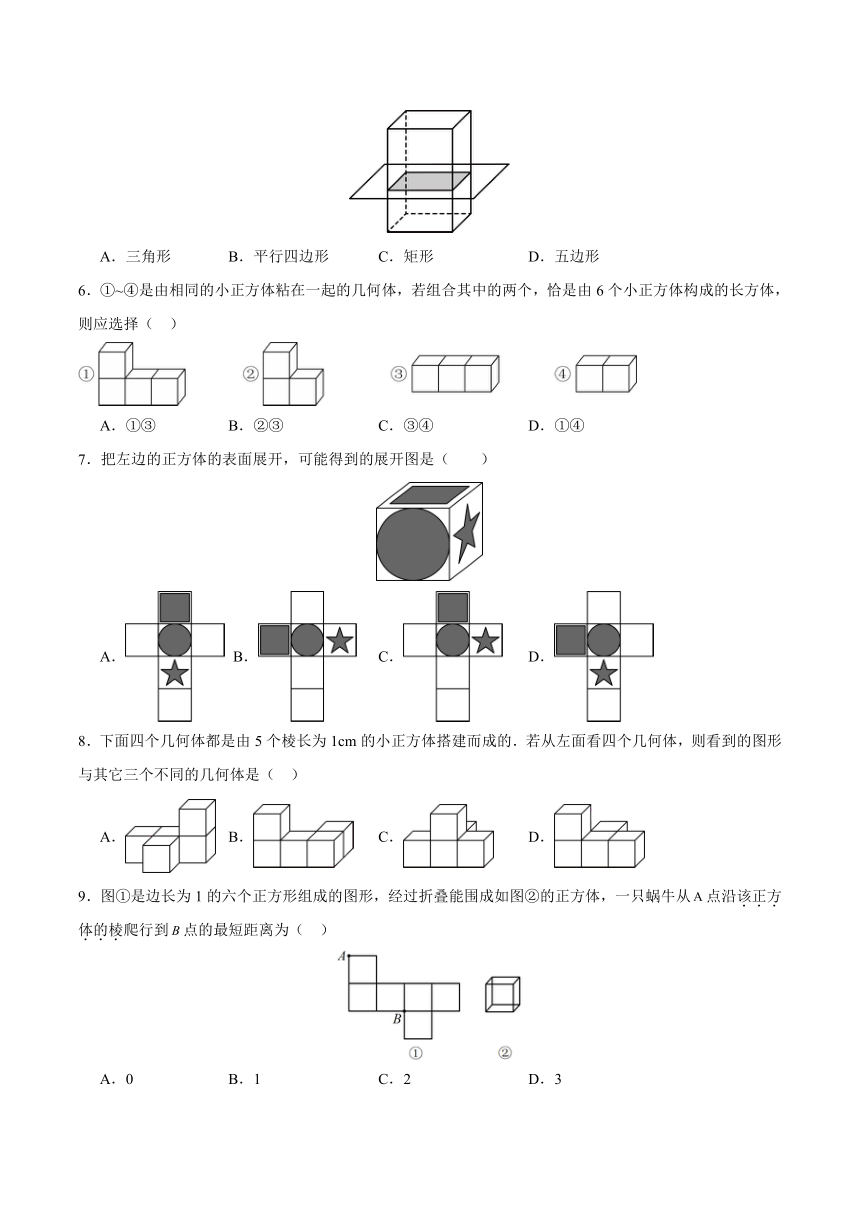
1.“力旺杯”足球赛在我校顺利进行,九年1班的足球队争得了冠军,如图所示为其获得的冠军奖杯,用数学的眼光观察这个奖杯,其中不包含的立体图形是( )
A.球体 B.圆柱体 C.长方体 D.四棱锥
2.下列几何体由5个平面围成的是( )
A.B.C. D.
3.下面现象说明“线动成面”的是( )
A.天空划过一道流星 B.扔一块小石子,石子在空中飞行的路线
C.旋转一扇门,门在空中运动的痕迹 D.汽车雨刷在挡风玻璃上面画出的痕迹
4.如图所示的花瓶中,其表面可以看作由如图的平面图形绕虚线旋转一周形成的是( )
A. B. C. D.
5.如图,用一个平行于长方体底面的平面截长方体,截面的形状是( )
A.三角形 B.平行四边形 C.矩形 D.五边形
6.①~④是由相同的小正方体粘在一起的几何体,若组合其中的两个,恰是由6个小正方体构成的长方体,则应选择( )
A.①③ B.②③ C.③④ D.①④
7.把左边的正方体的表面展开,可能得到的展开图是( )
A. B. C. D.
8.下面四个几何体都是由5个棱长为1cm的小正方体搭建而成的.若从左面看四个几何体,则看到的图形与其它三个不同的几何体是( )
A. B. C. D.
9.图①是边长为1的六个正方形组成的图形,经过折叠能围成如图②的正方体,一只蜗牛从点沿该正方体的棱爬行到点的最短距离为( )
A.0 B.1 C.2 D.3
10.一个六梭柱模型如图所示,它的底面边长都是,侧棱长是,该六棱柱的侧面积之和是( ).
A.120 B.20 C.100 D.150
二、填空题:共6题,每题3分,共18分。
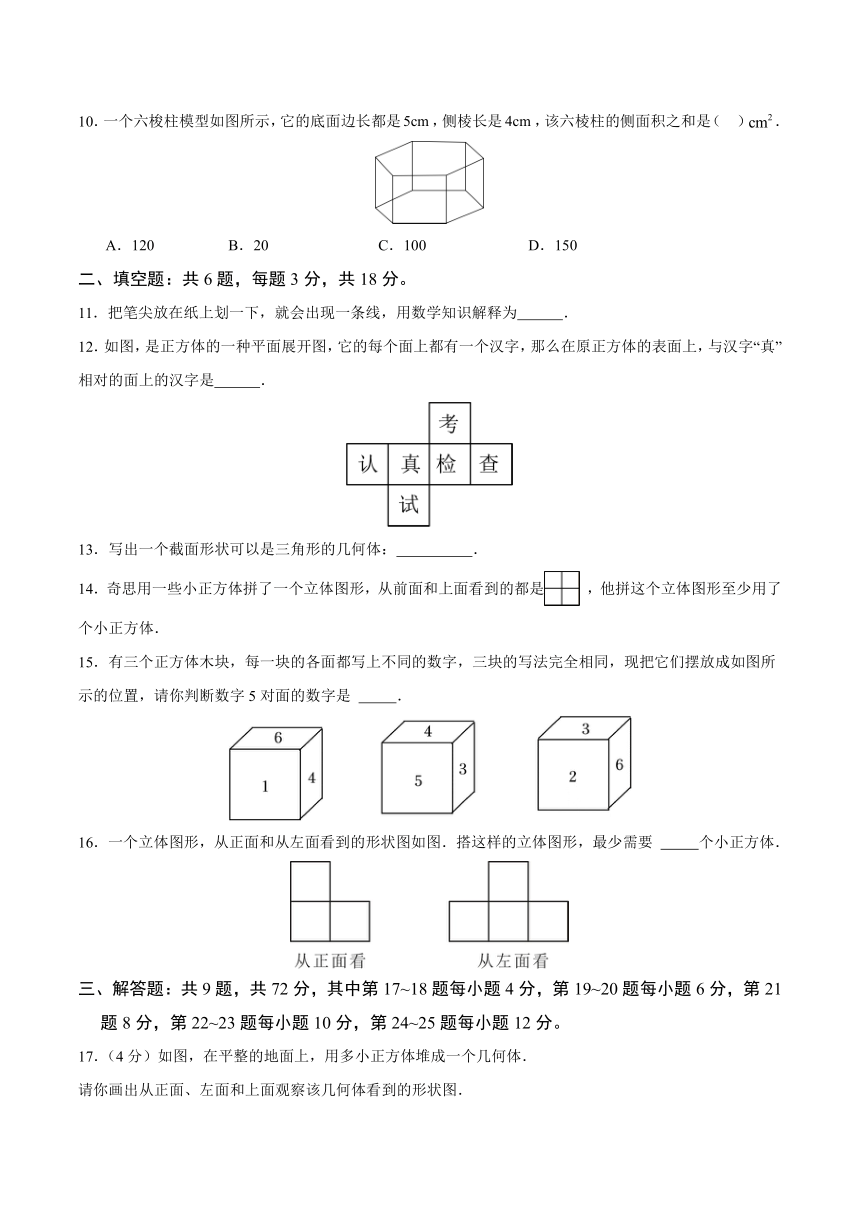
11.把笔尖放在纸上划一下,就会出现一条线,用数学知识解释为 .
12.如图,是正方体的一种平面展开图,它的每个面上都有一个汉字,那么在原正方体的表面上,与汉字“真”相对的面上的汉字是 .
13.写出一个截面形状可以是三角形的几何体: .
14.奇思用一些小正方体拼了一个立体图形,从前面和上面看到的都是 ,他拼这个立体图形至少用了 个小正方体.
15.有三个正方体木块,每一块的各面都写上不同的数字,三块的写法完全相同,现把它们摆放成如图所示的位置,请你判断数字5对面的数字是 .
16.一个立体图形,从正面和从左面看到的形状图如图.搭这样的立体图形,最少需要 个小正方体.
三、解答题:共9题,共72分,其中第17~18题每小题4分,第19~20题每小题6分,第21题8分,第22~23题每小题10分,第24~25题每小题12分。
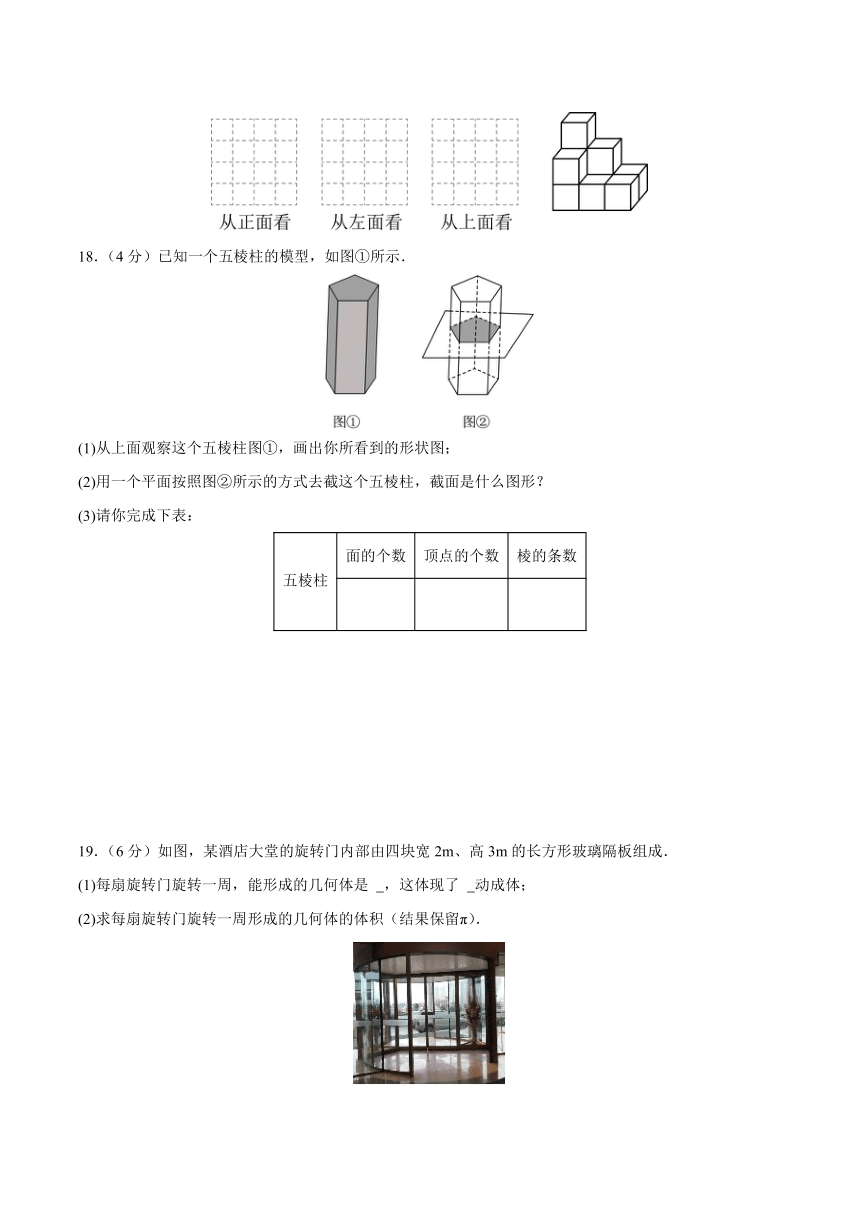
17.(4分)如图,在平整的地面上,用多小正方体堆成一个几何体.
请你画出从正面、左面和上面观察该几何体看到的形状图.
18.(4分)已知一个五棱柱的模型,如图①所示.
(1)从上面观察这个五棱柱图①,画出你所看到的形状图;
(2)用一个平面按照图②所示的方式去截这个五棱柱,截面是什么图形?
(3)请你完成下表:
五棱柱 面的个数 顶点的个数 棱的条数
19.(6分)如图,某酒店大堂的旋转门内部由四块宽2m、高3m的长方形玻璃隔板组成.
(1)每扇旋转门旋转一周,能形成的几何体是 ,这体现了 动成体;
(2)求每扇旋转门旋转一周形成的几何体的体积(结果保留π).
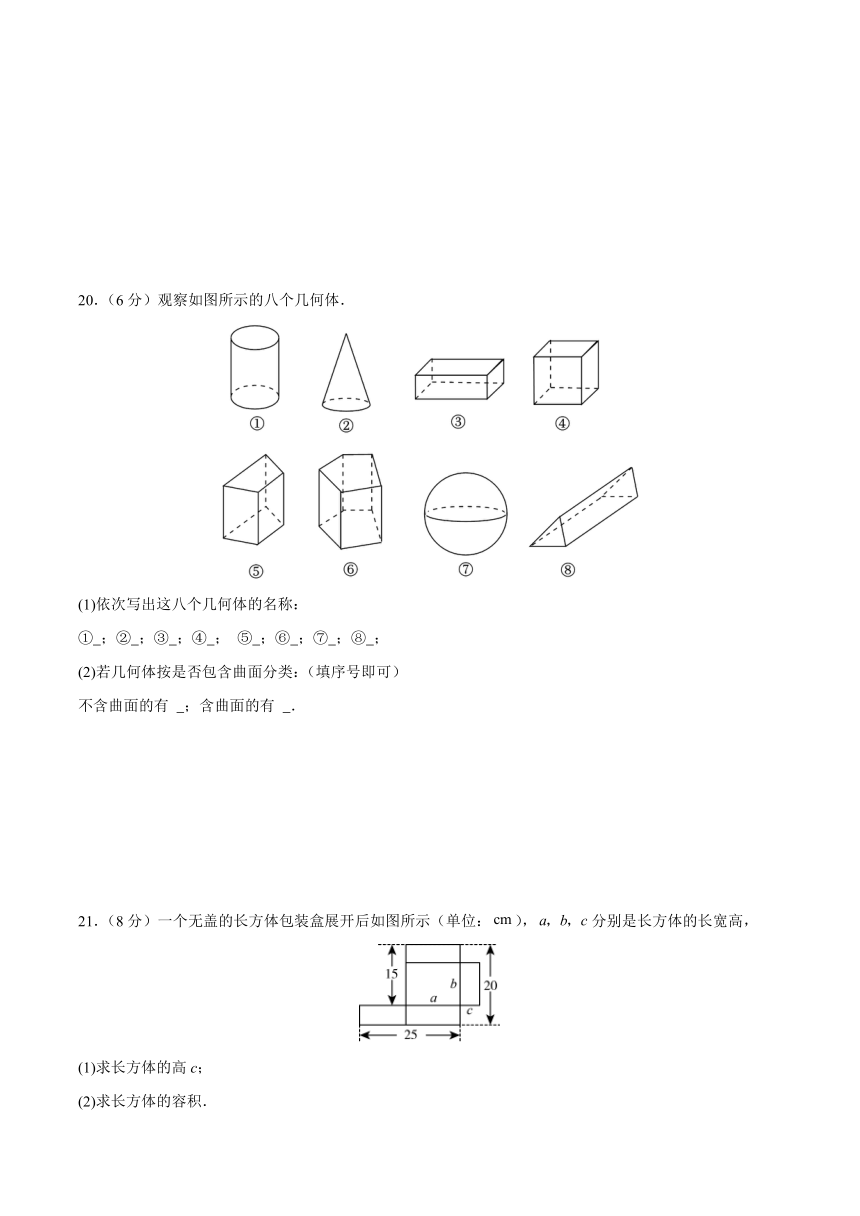
20.(6分)观察如图所示的八个几何体.
(1)依次写出这八个几何体的名称:
① ;② ;③ ;④ ; ⑤ ;⑥ ;⑦ ;⑧ ;
(2)若几何体按是否包含曲面分类:(填序号即可)
不含曲面的有 ;含曲面的有 .
21.(8分)一个无盖的长方体包装盒展开后如图所示(单位:),分别是长方体的长宽高,
(1)求长方体的高c;
(2)求长方体的容积.
22.(10分)如图所示的是从不同方向观察一个几何体得到的形状图
从正面看 从左面看 从上面看
(1)这个几何体的名称是______;
(2)由图中数据计算此几何体的侧面积(结果保留)
(3)画出该几何体的大致展开图.
23.(10分)如图所示是由几个小立方体所组成几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数.
(1)请在下面的网格中画出这个几何体从正面和从左面看到的图形;
(2)若小立方体的棱长为,求该几何体的表面积.
24.(12分)张明同学设计了某个产品的正方体包装盒如图所示,由于粗心少设计了其中一个顶盖,请你把它补上,使其成为一个两面均有盖的正方体盒子.
(1)共有______种弥补方法;
(2)任意画出一种成功的设计图(在图中补充);
(3)在你帮忙在设计成功的图中,把2,3,4,5,6,7这些数字分别填入六个小正方形,使得折成的正方体相对面上的两个数相加的和相等.(直接在图中填上)
25.(12分)小林所在的综合实践小组准备制作一些大小相同的正方体纸盒收纳班级讲台上的粉笔(盒盖单独制作).
(1)图1是综合实践小组同学制作的图形,其中______(填序号)经过折叠能围成无盖正方体纸盒;
(2)综合实践小组同学用制作的8个正方体纸盒摆成如图2所示的几何体.
①在图3中画出从正面观察图2几何体看到的形状图;
②如果在图2几何体上再添加一些相同的正方体纸盒,并保持从上面看到的形状图和从左面看到的形状图不变,最多可以再添加______个正方体纸盒.
第1章 丰富的图形世界(单元培优卷 北师大版)
考试时间:120分钟,满分:120分
选择题:共10题,每题3分,共30分。
1.“力旺杯”足球赛在我校顺利进行,九年1班的足球队争得了冠军,如图所示为其获得的冠军奖杯,用数学的眼光观察这个奖杯,其中不包含的立体图形是( )
A.球体 B.圆柱体 C.长方体 D.四棱锥
【答案】B
【详解】解:如图所示为其获得的冠军奖杯,用数学的眼光观察这个奖杯,其中不包含的立体图形是圆柱体.
故选:B.
2.下列几何体由5个平面围成的是( )
A.B.C. D.
【答案】C
【详解】A选项长方体是由六个平面围成,故本选项不符合题意;
B选项圆柱是由两个平面和1个曲面围成,故本选项不符合题意;
C选项三棱柱是由两个三角形和三个四边形围成,是由5个平面围成的,故本选项符合题意;
D选项圆锥是由一个曲面和一个圆围成的,故本选项符合题意.
故选:C.
3.下面现象说明“线动成面”的是( )
A.天空划过一道流星 B.扔一块小石子,石子在空中飞行的路线
C.旋转一扇门,门在空中运动的痕迹 D.汽车雨刷在挡风玻璃上面画出的痕迹
【答案】D
【详解】解:A、天空划过一道流星,说明“点动成线”,本选项不符合题意;
B、扔一块小石子,石子在空中飞行的路线,说明“点动成线”,本选项不符合题意;
C、旋转一扇门,门在空中运动的痕迹,说明“面动成体”,本选项不符合题意;
D、汽车雨刷在挡风玻璃上面画出的痕迹,说明“线动成面”,本选项符合题意.
故选:D.
4.如图所示的花瓶中,其表面可以看作由如图的平面图形绕虚线旋转一周形成的是( )
A. B. C. D.
【答案】B
【详解】解:由面动成体.由题目中的图示可知:此图形旋转可成脖子长有口的瓶子.
B是可由所给图形旋转而成的瓶型,故B正确;
故选:B.
5.如图,用一个平行于长方体底面的平面截长方体,截面的形状是( )
A.三角形 B.平行四边形 C.矩形 D.五边形
【答案】C
【详解】解:用一个平行于长方体底面的平面截长方体,截面的形状是长方形,
故选:C.
6.①~④是由相同的小正方体粘在一起的几何体,若组合其中的两个,恰是由6个小正方体构成的长方体,则应选择( )
A.①③ B.②③ C.③④ D.①④
【答案】D
【详解】解:观察图形可知,①~④的小正方体的个数分别为4,3,3,2,其中②③组合不能构成长方体,①④组合符合题意
故选D
7.把左边的正方体的表面展开,可能得到的展开图是( )
A. B. C. D.
【答案】C
【详解】解:由题意可知,“■”、“★”、“●”、三个图案应该相邻,
A、“■”与“★”图案相对,故不符合题意;
B、“■”与“★”图案相对,故不符合题意;
C、根据有图案的表面之间的位置关系,是正确的展开图;
D、“★”图案的位置应在“●”上面,故不符合题意.
故选:C.
8.下面四个几何体都是由5个棱长为1cm的小正方体搭建而成的.若从左面看四个几何体,则看到的图形与其它三个不同的几何体是( )
A. B. C. D.
【答案】A
【详解】
解:根据观察物体的方法, 从左面看到的形状都是 ,
从左面看到的形状是 ,
从左面看四个几何体,则看到的图形与其它三个不同的几何体是 .
故选:A.
9.图①是边长为1的六个正方形组成的图形,经过折叠能围成如图②的正方体,一只蜗牛从点沿该正方体的棱爬行到点的最短距离为( )
A.0 B.1 C.2 D.3
【答案】C
【详解】解:如图所示,将图①折成正方体后点、的在正方体中的位置,
蜗牛是从点沿该正方体的棱爬行到点
,
故选:C.
10.一个六梭柱模型如图所示,它的底面边长都是,侧棱长是,该六棱柱的侧面积之和是( ).
A.120 B.20 C.100 D.150
【答案】A
【详解】解:侧面积为:();
故选:A.
二、填空题:共6题,每题3分,共18分。
11.把笔尖放在纸上划一下,就会出现一条线,用数学知识解释为 .
【答案】点动成线
【详解】解:笔尖在纸上划一下,就会出现一条线,这说明了点动成线,
故答案为:点动成线.
12.如图,是正方体的一种平面展开图,它的每个面上都有一个汉字,那么在原正方体的表面上,与汉字“真”相对的面上的汉字是 .
【答案】查
【详解】解:正方体的平面展开图中相对的面一定是相隔一个小正方形,由图形可知,与“真”相对的字是“查”.
故答案为:查.
13.写出一个截面形状可以是三角形的几何体: .
【答案】长方形(答案不唯一)
【详解】解:截面形状可以是三角形的几何体有长方形,
故答案为:长方形(答案不唯一).
14.奇思用一些小正方体拼了一个立体图形,从前面和上面看到的都是 ,他拼这个立体图形至少用了 个小正方体.
【答案】6
【详解】解:从前面看到的图形可知,这个几何体有2层,上层至少有2个小正方体;从上面看到的图形可知,这个几何体的下层有4个小正方体,结合从前面和上面看到图形,可得出下面的几何体:
故他拼这个立体图形至少用了6个小正方体.
故答案为:6.
15.有三个正方体木块,每一块的各面都写上不同的数字,三块的写法完全相同,现把它们摆放成如图所示的位置,请你判断数字5对面的数字是 .
【答案】6
【详解】解:由第一个图得6与1,4相邻,由第三个图得6与2,3相邻,
∴6与5相对,
∴5对面的数字是6,
故答案为:6.
16.一个立体图形,从正面和从左面看到的形状图如图.搭这样的立体图形,最少需要 个小正方体.
【答案】4
【详解】解:如图,至少需要小正方体的个数是4个,从上面看到的图形如下:
故答案为:4.
三、解答题:共9题,共72分,其中第17~18题每小题4分,第19~20题每小题6分,第21题8分,第22~23题每小题10分,第24~25题每小题12分。
17.(4分)如图,在平整的地面上,用多小正方体堆成一个几何体.
请你画出从正面、左面和上面观察该几何体看到的形状图.
【答案】见解析
【详解】解:如图所示:
18.(4分)已知一个五棱柱的模型,如图①所示.
(1)从上面观察这个五棱柱图①,画出你所看到的形状图;
(2)用一个平面按照图②所示的方式去截这个五棱柱,截面是什么图形?
(3)请你完成下表:
五棱柱 面的个数 顶点的个数 棱的条数
【答案】(1)图形见解析;
(2)截面是五边形;
(3)表格见解析.
【详解】(1)解:如图所示:
(2)截面是五边形;
五棱柱 面的个数 顶点的个数 棱的条数
7 10 15
19.(6分)如图,某酒店大堂的旋转门内部由四块宽2m、高3m的长方形玻璃隔板组成.
(1)每扇旋转门旋转一周,能形成的几何体是 ,这体现了 动成体;
(2)求每扇旋转门旋转一周形成的几何体的体积(结果保留π).
【答案】(1)圆柱;面;
(2).
【详解】(1)解:每扇旋转门旋转一周,能形成的几何体是圆柱,这体现了面动成体,
故答案为:圆柱;面;
(2)解:由题意得:,
∴每扇旋转门旋转一周形成的几何体的体积.
20.(6分)观察如图所示的八个几何体.
(1)依次写出这八个几何体的名称:
① ;② ;③ ;④ ; ⑤ ;⑥ ;⑦ ;⑧ ;
(2)若几何体按是否包含曲面分类:(填序号即可)
不含曲面的有 ;含曲面的有 .
【答案】(1)圆柱;圆锥;长方体;正方体;四棱柱、五棱柱、球体;三棱柱
(2)③④⑤⑥⑧;①②⑦
【详解】(1)解:①圆柱;②圆锥;③长方体;④正方体;⑤四棱柱、⑥五棱柱、⑦球体;⑧三棱柱;
故答案为:圆柱;圆锥;长方体;正方体;四棱柱、五棱柱、球体;三棱柱.
(2)不含曲面的有:③④⑤⑥⑧;含曲面的有:①②⑦;
故答案为:③④⑤⑥⑧;①②⑦.
21.(8分)一个无盖的长方体包装盒展开后如图所示(单位:),分别是长方体的长宽高,
(1)求长方体的高c;
(2)求长方体的容积.
【答案】(1)长方体的高c的值为
(2)长方体的容积为
【详解】(1)解:
答:长方体的高c的值为;
(2)
.
答:长方体的容积为.
22.(10分)如图所示的是从不同方向观察一个几何体得到的形状图
从正面看 从左面看 从上面看
(1)这个几何体的名称是______;
(2)由图中数据计算此几何体的侧面积(结果保留)
(3)画出该几何体的大致展开图.
【答案】(1)圆柱
(2)
(3)见解析
【详解】(1)由从不同方向看到的形状可知该几何体是圆柱.
故答案为:圆柱;
(2)由图可知,圆柱体的底面直径为2,高为3,
所以侧面积.
(3)如图,
23.(10分)如图所示是由几个小立方体所组成几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数.
(1)请在下面的网格中画出这个几何体从正面和从左面看到的图形;
(2)若小立方体的棱长为,求该几何体的表面积.
【答案】(1)见解析
(2)
【详解】(1)如图所示:
(2)表面积为:.
故该几何体的表面积是.
24.(12分)张明同学设计了某个产品的正方体包装盒如图所示,由于粗心少设计了其中一个顶盖,请你把它补上,使其成为一个两面均有盖的正方体盒子.
(1)共有______种弥补方法;
(2)任意画出一种成功的设计图(在图中补充);
(3)在你帮忙在设计成功的图中,把2,3,4,5,6,7这些数字分别填入六个小正方形,使得折成的正方体相对面上的两个数相加的和相等.(直接在图中填上)
【答案】(1)4
(2)画图见解析
(3)画图见解析
【详解】(1)解:由正方体的展开图型特点,
可得共有4种弥补方法;
(2)设计其中一个顶盖,使其成为一个完整的正方体盒子,
如图所示,即是一个完整的正方体盒子,
答案不唯一;
(3)把2,3,4,5,6,7这些数字分别填入六个小正方形中,使折成的正方体相对面上的两个数相加的和相等,
如图所示,折成的正方体盒子相对面上的两个数相加都得9,
答案不唯一;
25.(12分)小林所在的综合实践小组准备制作一些大小相同的正方体纸盒收纳班级讲台上的粉笔(盒盖单独制作).
(1)图1是综合实践小组同学制作的图形,其中______(填序号)经过折叠能围成无盖正方体纸盒;
(2)综合实践小组同学用制作的8个正方体纸盒摆成如图2所示的几何体.
①在图3中画出从正面观察图2几何体看到的形状图;
②如果在图2几何体上再添加一些相同的正方体纸盒,并保持从上面看到的形状图和从左面看到的形状图不变,最多可以再添加______个正方体纸盒.
【答案】(1)①,③,④
(2)① 见解析② 3.
【详解】(1)解:由图可知:过折叠能围成无盖正方体纸盒的有①,③,④;
故答案为:①,③,④.
(2)①从正面看到的图形为:
②左边看有2列,第一列有3个,第二列有1个,从上面看有3列,每一列都有一个,要保持上面看到的形状图和从左面看到的形状图不变,最多可以在第二层加1个,第三层加2个,共3个正方体纸盒;
故答案为:3.
考试时间:120分钟,满分:120分
选择题:共10题,每题3分,共30分。
1.“力旺杯”足球赛在我校顺利进行,九年1班的足球队争得了冠军,如图所示为其获得的冠军奖杯,用数学的眼光观察这个奖杯,其中不包含的立体图形是( )
A.球体 B.圆柱体 C.长方体 D.四棱锥
2.下列几何体由5个平面围成的是( )
A.B.C. D.
3.下面现象说明“线动成面”的是( )
A.天空划过一道流星 B.扔一块小石子,石子在空中飞行的路线
C.旋转一扇门,门在空中运动的痕迹 D.汽车雨刷在挡风玻璃上面画出的痕迹
4.如图所示的花瓶中,其表面可以看作由如图的平面图形绕虚线旋转一周形成的是( )
A. B. C. D.
5.如图,用一个平行于长方体底面的平面截长方体,截面的形状是( )
A.三角形 B.平行四边形 C.矩形 D.五边形
6.①~④是由相同的小正方体粘在一起的几何体,若组合其中的两个,恰是由6个小正方体构成的长方体,则应选择( )
A.①③ B.②③ C.③④ D.①④
7.把左边的正方体的表面展开,可能得到的展开图是( )
A. B. C. D.
8.下面四个几何体都是由5个棱长为1cm的小正方体搭建而成的.若从左面看四个几何体,则看到的图形与其它三个不同的几何体是( )
A. B. C. D.
9.图①是边长为1的六个正方形组成的图形,经过折叠能围成如图②的正方体,一只蜗牛从点沿该正方体的棱爬行到点的最短距离为( )
A.0 B.1 C.2 D.3
10.一个六梭柱模型如图所示,它的底面边长都是,侧棱长是,该六棱柱的侧面积之和是( ).
A.120 B.20 C.100 D.150
二、填空题:共6题,每题3分,共18分。
11.把笔尖放在纸上划一下,就会出现一条线,用数学知识解释为 .
12.如图,是正方体的一种平面展开图,它的每个面上都有一个汉字,那么在原正方体的表面上,与汉字“真”相对的面上的汉字是 .
13.写出一个截面形状可以是三角形的几何体: .
14.奇思用一些小正方体拼了一个立体图形,从前面和上面看到的都是 ,他拼这个立体图形至少用了 个小正方体.
15.有三个正方体木块,每一块的各面都写上不同的数字,三块的写法完全相同,现把它们摆放成如图所示的位置,请你判断数字5对面的数字是 .
16.一个立体图形,从正面和从左面看到的形状图如图.搭这样的立体图形,最少需要 个小正方体.
三、解答题:共9题,共72分,其中第17~18题每小题4分,第19~20题每小题6分,第21题8分,第22~23题每小题10分,第24~25题每小题12分。
17.(4分)如图,在平整的地面上,用多小正方体堆成一个几何体.
请你画出从正面、左面和上面观察该几何体看到的形状图.
18.(4分)已知一个五棱柱的模型,如图①所示.
(1)从上面观察这个五棱柱图①,画出你所看到的形状图;
(2)用一个平面按照图②所示的方式去截这个五棱柱,截面是什么图形?
(3)请你完成下表:
五棱柱 面的个数 顶点的个数 棱的条数
19.(6分)如图,某酒店大堂的旋转门内部由四块宽2m、高3m的长方形玻璃隔板组成.
(1)每扇旋转门旋转一周,能形成的几何体是 ,这体现了 动成体;
(2)求每扇旋转门旋转一周形成的几何体的体积(结果保留π).
20.(6分)观察如图所示的八个几何体.
(1)依次写出这八个几何体的名称:
① ;② ;③ ;④ ; ⑤ ;⑥ ;⑦ ;⑧ ;
(2)若几何体按是否包含曲面分类:(填序号即可)
不含曲面的有 ;含曲面的有 .
21.(8分)一个无盖的长方体包装盒展开后如图所示(单位:),分别是长方体的长宽高,
(1)求长方体的高c;
(2)求长方体的容积.
22.(10分)如图所示的是从不同方向观察一个几何体得到的形状图
从正面看 从左面看 从上面看
(1)这个几何体的名称是______;
(2)由图中数据计算此几何体的侧面积(结果保留)
(3)画出该几何体的大致展开图.
23.(10分)如图所示是由几个小立方体所组成几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数.
(1)请在下面的网格中画出这个几何体从正面和从左面看到的图形;
(2)若小立方体的棱长为,求该几何体的表面积.
24.(12分)张明同学设计了某个产品的正方体包装盒如图所示,由于粗心少设计了其中一个顶盖,请你把它补上,使其成为一个两面均有盖的正方体盒子.
(1)共有______种弥补方法;
(2)任意画出一种成功的设计图(在图中补充);
(3)在你帮忙在设计成功的图中,把2,3,4,5,6,7这些数字分别填入六个小正方形,使得折成的正方体相对面上的两个数相加的和相等.(直接在图中填上)
25.(12分)小林所在的综合实践小组准备制作一些大小相同的正方体纸盒收纳班级讲台上的粉笔(盒盖单独制作).
(1)图1是综合实践小组同学制作的图形,其中______(填序号)经过折叠能围成无盖正方体纸盒;
(2)综合实践小组同学用制作的8个正方体纸盒摆成如图2所示的几何体.
①在图3中画出从正面观察图2几何体看到的形状图;
②如果在图2几何体上再添加一些相同的正方体纸盒,并保持从上面看到的形状图和从左面看到的形状图不变,最多可以再添加______个正方体纸盒.
第1章 丰富的图形世界(单元培优卷 北师大版)
考试时间:120分钟,满分:120分
选择题:共10题,每题3分,共30分。
1.“力旺杯”足球赛在我校顺利进行,九年1班的足球队争得了冠军,如图所示为其获得的冠军奖杯,用数学的眼光观察这个奖杯,其中不包含的立体图形是( )
A.球体 B.圆柱体 C.长方体 D.四棱锥
【答案】B
【详解】解:如图所示为其获得的冠军奖杯,用数学的眼光观察这个奖杯,其中不包含的立体图形是圆柱体.
故选:B.
2.下列几何体由5个平面围成的是( )
A.B.C. D.
【答案】C
【详解】A选项长方体是由六个平面围成,故本选项不符合题意;
B选项圆柱是由两个平面和1个曲面围成,故本选项不符合题意;
C选项三棱柱是由两个三角形和三个四边形围成,是由5个平面围成的,故本选项符合题意;
D选项圆锥是由一个曲面和一个圆围成的,故本选项符合题意.
故选:C.
3.下面现象说明“线动成面”的是( )
A.天空划过一道流星 B.扔一块小石子,石子在空中飞行的路线
C.旋转一扇门,门在空中运动的痕迹 D.汽车雨刷在挡风玻璃上面画出的痕迹
【答案】D
【详解】解:A、天空划过一道流星,说明“点动成线”,本选项不符合题意;
B、扔一块小石子,石子在空中飞行的路线,说明“点动成线”,本选项不符合题意;
C、旋转一扇门,门在空中运动的痕迹,说明“面动成体”,本选项不符合题意;
D、汽车雨刷在挡风玻璃上面画出的痕迹,说明“线动成面”,本选项符合题意.
故选:D.
4.如图所示的花瓶中,其表面可以看作由如图的平面图形绕虚线旋转一周形成的是( )
A. B. C. D.
【答案】B
【详解】解:由面动成体.由题目中的图示可知:此图形旋转可成脖子长有口的瓶子.
B是可由所给图形旋转而成的瓶型,故B正确;
故选:B.
5.如图,用一个平行于长方体底面的平面截长方体,截面的形状是( )
A.三角形 B.平行四边形 C.矩形 D.五边形
【答案】C
【详解】解:用一个平行于长方体底面的平面截长方体,截面的形状是长方形,
故选:C.
6.①~④是由相同的小正方体粘在一起的几何体,若组合其中的两个,恰是由6个小正方体构成的长方体,则应选择( )
A.①③ B.②③ C.③④ D.①④
【答案】D
【详解】解:观察图形可知,①~④的小正方体的个数分别为4,3,3,2,其中②③组合不能构成长方体,①④组合符合题意
故选D
7.把左边的正方体的表面展开,可能得到的展开图是( )
A. B. C. D.
【答案】C
【详解】解:由题意可知,“■”、“★”、“●”、三个图案应该相邻,
A、“■”与“★”图案相对,故不符合题意;
B、“■”与“★”图案相对,故不符合题意;
C、根据有图案的表面之间的位置关系,是正确的展开图;
D、“★”图案的位置应在“●”上面,故不符合题意.
故选:C.
8.下面四个几何体都是由5个棱长为1cm的小正方体搭建而成的.若从左面看四个几何体,则看到的图形与其它三个不同的几何体是( )
A. B. C. D.
【答案】A
【详解】
解:根据观察物体的方法, 从左面看到的形状都是 ,
从左面看到的形状是 ,
从左面看四个几何体,则看到的图形与其它三个不同的几何体是 .
故选:A.
9.图①是边长为1的六个正方形组成的图形,经过折叠能围成如图②的正方体,一只蜗牛从点沿该正方体的棱爬行到点的最短距离为( )
A.0 B.1 C.2 D.3
【答案】C
【详解】解:如图所示,将图①折成正方体后点、的在正方体中的位置,
蜗牛是从点沿该正方体的棱爬行到点
,
故选:C.
10.一个六梭柱模型如图所示,它的底面边长都是,侧棱长是,该六棱柱的侧面积之和是( ).
A.120 B.20 C.100 D.150
【答案】A
【详解】解:侧面积为:();
故选:A.
二、填空题:共6题,每题3分,共18分。
11.把笔尖放在纸上划一下,就会出现一条线,用数学知识解释为 .
【答案】点动成线
【详解】解:笔尖在纸上划一下,就会出现一条线,这说明了点动成线,
故答案为:点动成线.
12.如图,是正方体的一种平面展开图,它的每个面上都有一个汉字,那么在原正方体的表面上,与汉字“真”相对的面上的汉字是 .
【答案】查
【详解】解:正方体的平面展开图中相对的面一定是相隔一个小正方形,由图形可知,与“真”相对的字是“查”.
故答案为:查.
13.写出一个截面形状可以是三角形的几何体: .
【答案】长方形(答案不唯一)
【详解】解:截面形状可以是三角形的几何体有长方形,
故答案为:长方形(答案不唯一).
14.奇思用一些小正方体拼了一个立体图形,从前面和上面看到的都是 ,他拼这个立体图形至少用了 个小正方体.
【答案】6
【详解】解:从前面看到的图形可知,这个几何体有2层,上层至少有2个小正方体;从上面看到的图形可知,这个几何体的下层有4个小正方体,结合从前面和上面看到图形,可得出下面的几何体:
故他拼这个立体图形至少用了6个小正方体.
故答案为:6.
15.有三个正方体木块,每一块的各面都写上不同的数字,三块的写法完全相同,现把它们摆放成如图所示的位置,请你判断数字5对面的数字是 .
【答案】6
【详解】解:由第一个图得6与1,4相邻,由第三个图得6与2,3相邻,
∴6与5相对,
∴5对面的数字是6,
故答案为:6.
16.一个立体图形,从正面和从左面看到的形状图如图.搭这样的立体图形,最少需要 个小正方体.
【答案】4
【详解】解:如图,至少需要小正方体的个数是4个,从上面看到的图形如下:
故答案为:4.
三、解答题:共9题,共72分,其中第17~18题每小题4分,第19~20题每小题6分,第21题8分,第22~23题每小题10分,第24~25题每小题12分。
17.(4分)如图,在平整的地面上,用多小正方体堆成一个几何体.
请你画出从正面、左面和上面观察该几何体看到的形状图.
【答案】见解析
【详解】解:如图所示:
18.(4分)已知一个五棱柱的模型,如图①所示.
(1)从上面观察这个五棱柱图①,画出你所看到的形状图;
(2)用一个平面按照图②所示的方式去截这个五棱柱,截面是什么图形?
(3)请你完成下表:
五棱柱 面的个数 顶点的个数 棱的条数
【答案】(1)图形见解析;
(2)截面是五边形;
(3)表格见解析.
【详解】(1)解:如图所示:
(2)截面是五边形;
五棱柱 面的个数 顶点的个数 棱的条数
7 10 15
19.(6分)如图,某酒店大堂的旋转门内部由四块宽2m、高3m的长方形玻璃隔板组成.
(1)每扇旋转门旋转一周,能形成的几何体是 ,这体现了 动成体;
(2)求每扇旋转门旋转一周形成的几何体的体积(结果保留π).
【答案】(1)圆柱;面;
(2).
【详解】(1)解:每扇旋转门旋转一周,能形成的几何体是圆柱,这体现了面动成体,
故答案为:圆柱;面;
(2)解:由题意得:,
∴每扇旋转门旋转一周形成的几何体的体积.
20.(6分)观察如图所示的八个几何体.
(1)依次写出这八个几何体的名称:
① ;② ;③ ;④ ; ⑤ ;⑥ ;⑦ ;⑧ ;
(2)若几何体按是否包含曲面分类:(填序号即可)
不含曲面的有 ;含曲面的有 .
【答案】(1)圆柱;圆锥;长方体;正方体;四棱柱、五棱柱、球体;三棱柱
(2)③④⑤⑥⑧;①②⑦
【详解】(1)解:①圆柱;②圆锥;③长方体;④正方体;⑤四棱柱、⑥五棱柱、⑦球体;⑧三棱柱;
故答案为:圆柱;圆锥;长方体;正方体;四棱柱、五棱柱、球体;三棱柱.
(2)不含曲面的有:③④⑤⑥⑧;含曲面的有:①②⑦;
故答案为:③④⑤⑥⑧;①②⑦.
21.(8分)一个无盖的长方体包装盒展开后如图所示(单位:),分别是长方体的长宽高,
(1)求长方体的高c;
(2)求长方体的容积.
【答案】(1)长方体的高c的值为
(2)长方体的容积为
【详解】(1)解:
答:长方体的高c的值为;
(2)
.
答:长方体的容积为.
22.(10分)如图所示的是从不同方向观察一个几何体得到的形状图
从正面看 从左面看 从上面看
(1)这个几何体的名称是______;
(2)由图中数据计算此几何体的侧面积(结果保留)
(3)画出该几何体的大致展开图.
【答案】(1)圆柱
(2)
(3)见解析
【详解】(1)由从不同方向看到的形状可知该几何体是圆柱.
故答案为:圆柱;
(2)由图可知,圆柱体的底面直径为2,高为3,
所以侧面积.
(3)如图,
23.(10分)如图所示是由几个小立方体所组成几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数.
(1)请在下面的网格中画出这个几何体从正面和从左面看到的图形;
(2)若小立方体的棱长为,求该几何体的表面积.
【答案】(1)见解析
(2)
【详解】(1)如图所示:
(2)表面积为:.
故该几何体的表面积是.
24.(12分)张明同学设计了某个产品的正方体包装盒如图所示,由于粗心少设计了其中一个顶盖,请你把它补上,使其成为一个两面均有盖的正方体盒子.
(1)共有______种弥补方法;
(2)任意画出一种成功的设计图(在图中补充);
(3)在你帮忙在设计成功的图中,把2,3,4,5,6,7这些数字分别填入六个小正方形,使得折成的正方体相对面上的两个数相加的和相等.(直接在图中填上)
【答案】(1)4
(2)画图见解析
(3)画图见解析
【详解】(1)解:由正方体的展开图型特点,
可得共有4种弥补方法;
(2)设计其中一个顶盖,使其成为一个完整的正方体盒子,
如图所示,即是一个完整的正方体盒子,
答案不唯一;
(3)把2,3,4,5,6,7这些数字分别填入六个小正方形中,使折成的正方体相对面上的两个数相加的和相等,
如图所示,折成的正方体盒子相对面上的两个数相加都得9,
答案不唯一;
25.(12分)小林所在的综合实践小组准备制作一些大小相同的正方体纸盒收纳班级讲台上的粉笔(盒盖单独制作).
(1)图1是综合实践小组同学制作的图形,其中______(填序号)经过折叠能围成无盖正方体纸盒;
(2)综合实践小组同学用制作的8个正方体纸盒摆成如图2所示的几何体.
①在图3中画出从正面观察图2几何体看到的形状图;
②如果在图2几何体上再添加一些相同的正方体纸盒,并保持从上面看到的形状图和从左面看到的形状图不变,最多可以再添加______个正方体纸盒.
【答案】(1)①,③,④
(2)① 见解析② 3.
【详解】(1)解:由图可知:过折叠能围成无盖正方体纸盒的有①,③,④;
故答案为:①,③,④.
(2)①从正面看到的图形为:
②左边看有2列,第一列有3个,第二列有1个,从上面看有3列,每一列都有一个,要保持上面看到的形状图和从左面看到的形状图不变,最多可以在第二层加1个,第三层加2个,共3个正方体纸盒;
故答案为:3.
同课章节目录
