6.2.2 组合与组合数 教学设计(表格式)
文档属性
| 名称 | 6.2.2 组合与组合数 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 19.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-04 00:00:00 | ||
图片预览


文档简介
《6.2.3 & 6.2.4 组合与组合数》教学设计
教学内容分析
本节课内容出自选择性必修三《第六章 计数原理》,排列与组合作为计数问题,是两个基本的计数模型,具有广泛的应用,在第六章的二项式定理以及第七章的二项分布和超几何分布中就有所体现。排列是学习组合的基础。在本节课,学生需要重点提高的是运用排列和组合这两个数学工具,将问题用排列或组合来解决。 本节教学的重点是组合的理解,难点是运用组合以及组合数公式解决问题。组合与排列的区别是基本重要的。 在对组合的理解上,要对组合问题不计较顺序这一点加以说明,进而说明排列与组合的区别,从而达到学生充分理解组合的概念的目的。在这一点上,教材把排列的例题变形成一个组合问题,将两道题进行对比,通过类比引出组合的定义。在引入组合的概念中,从例题来认识一般的组合问题,体现了从特殊到一般的数学思想。教材还对排列与组合之间的联系与区别进行了进一步的解释说明,为组合数公式的推导做了铺垫。 在推导组合数公式的过程中,又进行了说明,将排列问题理解为先组合再求全排列,从而列出等式,得到组合数公式。在这一过程中,课本提出了一个探究——“如何由排列数来求组合数”。课本以“4个元素取3个”为例进行说明,讲了两种由排列数求组合数的方法,但不足之处在于,课本将两种方法混杂,并且没有讲清楚第一种方法。熊老师在课堂上提出的公式推导过程中,问题“根据排列写出组合”以及反问题“根据组合写出排列”可以很好地兼顾两种方法。
重难点
理解组合的定义,理解排列和组合的区别。 2、能运用组合模型解决简单的计数问题
教学目标
理解组合的定义,理解排列和组合的区别。 能运用组合模型解决简单的计数问题。 培养一定的分析问题、解决问题的能力。
教学过程设计
教学环节 教学时间 教学内容 教师活动 学生活动 设计意图
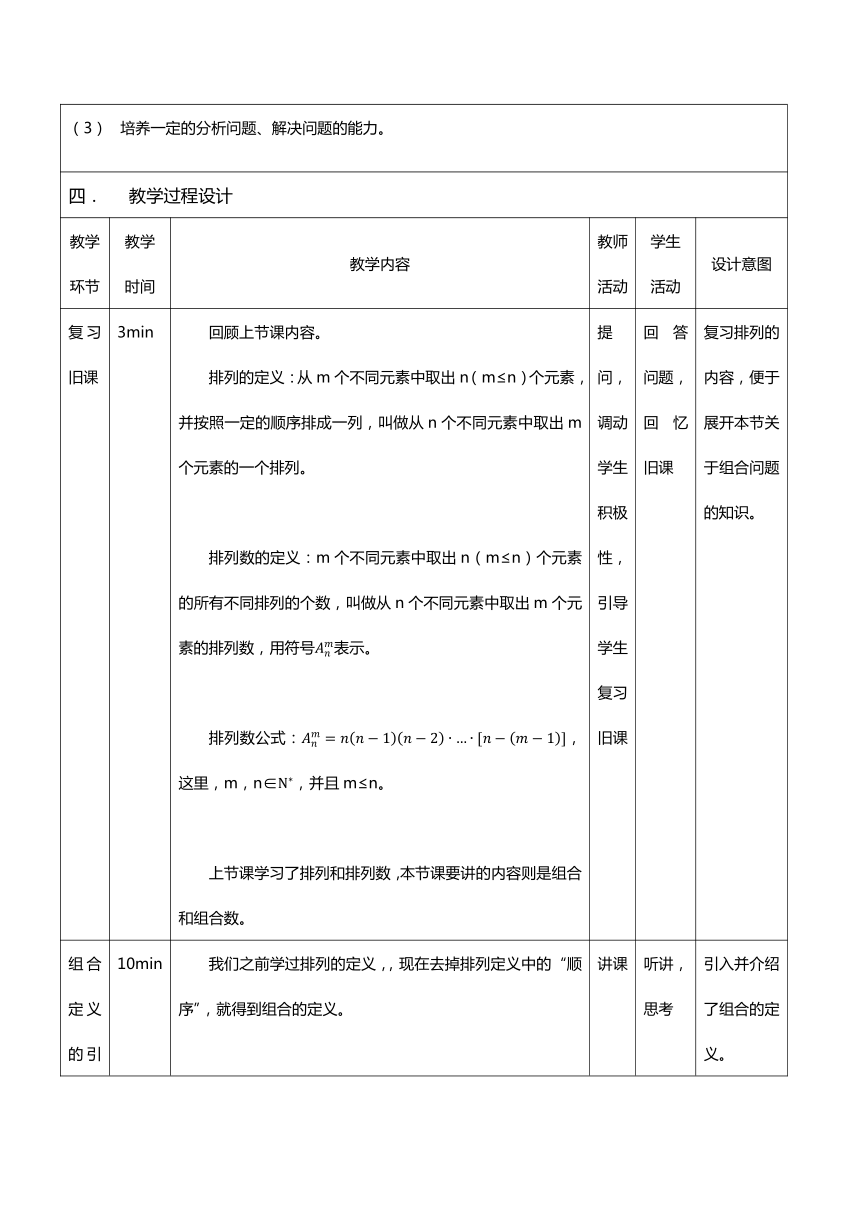
复习旧课 3min 回顾上节课内容。 排列的定义:从m个不同元素中取出n(m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列。 排列数的定义:m个不同元素中取出n(m≤n)个元素的所有不同排列的个数,叫做从n个不同元素中取出m个元素的排列数,用符号表示。 排列数公式:,这里,m,n∈,并且m≤n。 上节课学习了排列和排列数,本节课要讲的内容则是组合和组合数。 提问,调动学生积极性,引导学生复习旧课 回答问题,回忆旧课 复习排列的内容,便于展开本节关于组合问题的知识。
组合定义的引入 10min 我们之前学过排列的定义,,现在去掉排列定义中的“顺序”,就得到组合的定义。 组合的定义: 一般地,从m个不同元素中取出n(m≤n)个元素作为一组,叫做从n个不同元素中取出m个元素的一个组合。 进行小组讨论:根据排列与组合的定义,结合刚刚所学的例题,讨论排列和组合有什么共同点?又有什么区别? 两者的共同点在于,都是从m个不同元素中取出n(m≤n)个元素的计数问题。 区别在于,排列需要考虑元素顺序,组合不需要考虑元素顺序。以前面的例题为例,在排列问题中,“甲乙”和“乙甲”是两种不同的情况,而在组合问题中,“甲乙”和“乙甲”则认为是相同的。 讲课 听讲,思考 引入并介绍了组合的定义。
排列定义的巩固练习 8min 先来回顾上节课的一个问题。 从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有6种不同的选法。 现在把问题进行改变,如下。 例题1:从甲、乙、丙3名同学中选2名去参加一项活动,有多少种不同的选法? 解:列举法。相比于排列问题,此时只需考虑3名同学中选哪2名,而不需要考虑选出的两名同学哪名参加上午的活动,哪名参加下午的活动。 因而有甲乙,甲丙,乙丙,共3种不同的选法。 像这样的问题称为组合问题。 进行小组讨论:根据排列与组合的定义,结合刚刚所学的例题,讨论排列和组合有什么共同点?又有什么区别? 两者的共同点在于,都是从m个不同元素中取出n(m≤n)个元素的计数问题。 区别在于,排列需要考虑元素顺序,组合不需要考虑元素顺序。以前面的例题为例,在排列问题中,“甲乙”和“乙甲”是两种不同的情况,而在组合问题中,“甲乙”和“乙甲”则认为是相同的。 讲课 听讲,思考 引入组合问题,与排列进行比较,重点在于理解组合问题不计较顺序,注意区分排列和组合
组合数的概念 5min 组合数概念: 从m个不同元素中取出n(m≤n)个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号表示。 例如,从3个不同元素中取出2个元素的组合数表示为,指从3个不同元素中取出2个元素有种不同的取法。 讲课 听讲,思考 引入组合数的概念。
练习巩固 4min 平面内有A,B,C,D共4个点. (1)以其中2个点为端点的有向线段共有多少条? (2)以其中2个点为端点的线段共有多少条? 讲解题目 思考,回答问题 对组合问题进行练习巩固。
组合数公式及推导 12min 问题1: a,b,c,d,e共5个元素,从其中写出3个元素的所有排列。在书写中,注意不重复、不遗漏。 学生:abc,acb,bac,bca,cab,cba;abd,adb,bad,bda,dab,dba;abe,…;acd,…;ace,…;ade…。共36种。 问题2: a,b,c,d,e共5个元素,从其中写出3个元素的所有组合。 学生:abc,abd,abe,acd,ace,ade。共6种。 问题3:能否根据排列写出组合? 学生:对于含有相同元素的6个排列,对应一个组合,以“元素相同”为标准对所有排列进行分组,共6组,每组对应一个组合,也就是组合共6种。 问题4:能否根据组合写出排列? 学生:对一个组合的元素,进行全排列,有种排列方式,也就是一个组合对应6个排列。 教师:那么也就是有,排列数是组合数的倍,可以先列出式子以待证明。 求 “从n个元素中取出m个元素的排列数”,可以看作由以下两个步骤得到: 第1步,从从n个元素中取出m个元素作为一组,共有种不同的取法; 第2步,将取出的n个元素作全排列,共有种不同的排法。 根据分步乘法计数原理,有=。 因此,. 这里,m,n∈,并且m≤n.这个公式叫做组合数公式. 上面的组合数公式还可以写成 讲课 听讲,思考 对组合数公式进行推导,采用了先猜后证的方法,先对公式进行引入,再猜出公式并进行证明。在引入过程中,学生还增进了对“如何由排列数求组合数”的认识,便于开展后续的证明过程。
练习巩固 3min 计算:(1);(2) ;(3) ;(4) . 在100件产品中,有98件合格品,2件次品.从这100件产品中任意抽出3件. (1)有多少种不同的抽法? (2)抽出的3件中恰好有1件是次品的抽法有多少种? (3)抽出的3件中至少有1件是次品的抽法有多少种? 答疑解惑 练习 练习巩固
教学内容分析
本节课内容出自选择性必修三《第六章 计数原理》,排列与组合作为计数问题,是两个基本的计数模型,具有广泛的应用,在第六章的二项式定理以及第七章的二项分布和超几何分布中就有所体现。排列是学习组合的基础。在本节课,学生需要重点提高的是运用排列和组合这两个数学工具,将问题用排列或组合来解决。 本节教学的重点是组合的理解,难点是运用组合以及组合数公式解决问题。组合与排列的区别是基本重要的。 在对组合的理解上,要对组合问题不计较顺序这一点加以说明,进而说明排列与组合的区别,从而达到学生充分理解组合的概念的目的。在这一点上,教材把排列的例题变形成一个组合问题,将两道题进行对比,通过类比引出组合的定义。在引入组合的概念中,从例题来认识一般的组合问题,体现了从特殊到一般的数学思想。教材还对排列与组合之间的联系与区别进行了进一步的解释说明,为组合数公式的推导做了铺垫。 在推导组合数公式的过程中,又进行了说明,将排列问题理解为先组合再求全排列,从而列出等式,得到组合数公式。在这一过程中,课本提出了一个探究——“如何由排列数来求组合数”。课本以“4个元素取3个”为例进行说明,讲了两种由排列数求组合数的方法,但不足之处在于,课本将两种方法混杂,并且没有讲清楚第一种方法。熊老师在课堂上提出的公式推导过程中,问题“根据排列写出组合”以及反问题“根据组合写出排列”可以很好地兼顾两种方法。
重难点
理解组合的定义,理解排列和组合的区别。 2、能运用组合模型解决简单的计数问题
教学目标
理解组合的定义,理解排列和组合的区别。 能运用组合模型解决简单的计数问题。 培养一定的分析问题、解决问题的能力。
教学过程设计
教学环节 教学时间 教学内容 教师活动 学生活动 设计意图
复习旧课 3min 回顾上节课内容。 排列的定义:从m个不同元素中取出n(m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列。 排列数的定义:m个不同元素中取出n(m≤n)个元素的所有不同排列的个数,叫做从n个不同元素中取出m个元素的排列数,用符号表示。 排列数公式:,这里,m,n∈,并且m≤n。 上节课学习了排列和排列数,本节课要讲的内容则是组合和组合数。 提问,调动学生积极性,引导学生复习旧课 回答问题,回忆旧课 复习排列的内容,便于展开本节关于组合问题的知识。
组合定义的引入 10min 我们之前学过排列的定义,,现在去掉排列定义中的“顺序”,就得到组合的定义。 组合的定义: 一般地,从m个不同元素中取出n(m≤n)个元素作为一组,叫做从n个不同元素中取出m个元素的一个组合。 进行小组讨论:根据排列与组合的定义,结合刚刚所学的例题,讨论排列和组合有什么共同点?又有什么区别? 两者的共同点在于,都是从m个不同元素中取出n(m≤n)个元素的计数问题。 区别在于,排列需要考虑元素顺序,组合不需要考虑元素顺序。以前面的例题为例,在排列问题中,“甲乙”和“乙甲”是两种不同的情况,而在组合问题中,“甲乙”和“乙甲”则认为是相同的。 讲课 听讲,思考 引入并介绍了组合的定义。
排列定义的巩固练习 8min 先来回顾上节课的一个问题。 从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有6种不同的选法。 现在把问题进行改变,如下。 例题1:从甲、乙、丙3名同学中选2名去参加一项活动,有多少种不同的选法? 解:列举法。相比于排列问题,此时只需考虑3名同学中选哪2名,而不需要考虑选出的两名同学哪名参加上午的活动,哪名参加下午的活动。 因而有甲乙,甲丙,乙丙,共3种不同的选法。 像这样的问题称为组合问题。 进行小组讨论:根据排列与组合的定义,结合刚刚所学的例题,讨论排列和组合有什么共同点?又有什么区别? 两者的共同点在于,都是从m个不同元素中取出n(m≤n)个元素的计数问题。 区别在于,排列需要考虑元素顺序,组合不需要考虑元素顺序。以前面的例题为例,在排列问题中,“甲乙”和“乙甲”是两种不同的情况,而在组合问题中,“甲乙”和“乙甲”则认为是相同的。 讲课 听讲,思考 引入组合问题,与排列进行比较,重点在于理解组合问题不计较顺序,注意区分排列和组合
组合数的概念 5min 组合数概念: 从m个不同元素中取出n(m≤n)个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号表示。 例如,从3个不同元素中取出2个元素的组合数表示为,指从3个不同元素中取出2个元素有种不同的取法。 讲课 听讲,思考 引入组合数的概念。
练习巩固 4min 平面内有A,B,C,D共4个点. (1)以其中2个点为端点的有向线段共有多少条? (2)以其中2个点为端点的线段共有多少条? 讲解题目 思考,回答问题 对组合问题进行练习巩固。
组合数公式及推导 12min 问题1: a,b,c,d,e共5个元素,从其中写出3个元素的所有排列。在书写中,注意不重复、不遗漏。 学生:abc,acb,bac,bca,cab,cba;abd,adb,bad,bda,dab,dba;abe,…;acd,…;ace,…;ade…。共36种。 问题2: a,b,c,d,e共5个元素,从其中写出3个元素的所有组合。 学生:abc,abd,abe,acd,ace,ade。共6种。 问题3:能否根据排列写出组合? 学生:对于含有相同元素的6个排列,对应一个组合,以“元素相同”为标准对所有排列进行分组,共6组,每组对应一个组合,也就是组合共6种。 问题4:能否根据组合写出排列? 学生:对一个组合的元素,进行全排列,有种排列方式,也就是一个组合对应6个排列。 教师:那么也就是有,排列数是组合数的倍,可以先列出式子以待证明。 求 “从n个元素中取出m个元素的排列数”,可以看作由以下两个步骤得到: 第1步,从从n个元素中取出m个元素作为一组,共有种不同的取法; 第2步,将取出的n个元素作全排列,共有种不同的排法。 根据分步乘法计数原理,有=。 因此,. 这里,m,n∈,并且m≤n.这个公式叫做组合数公式. 上面的组合数公式还可以写成 讲课 听讲,思考 对组合数公式进行推导,采用了先猜后证的方法,先对公式进行引入,再猜出公式并进行证明。在引入过程中,学生还增进了对“如何由排列数求组合数”的认识,便于开展后续的证明过程。
练习巩固 3min 计算:(1);(2) ;(3) ;(4) . 在100件产品中,有98件合格品,2件次品.从这100件产品中任意抽出3件. (1)有多少种不同的抽法? (2)抽出的3件中恰好有1件是次品的抽法有多少种? (3)抽出的3件中至少有1件是次品的抽法有多少种? 答疑解惑 练习 练习巩固
