3.2 第1课时平面直角坐标系的有关概念 教案(表格式) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 3.2 第1课时平面直角坐标系的有关概念 教案(表格式) 2025-2026学年数学北师大版(2024)八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 277.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-04 00:00:00 | ||
图片预览

文档简介
第1课时 平面直角坐标系的有关概念
课标摘录 1.理解平面直角坐标系的有关概念,能画出平面直角坐标系;在给定的平面直角坐标系中,能根据坐标描出点的位置,由点的位置写出坐标。 2.在实际问题中,能建立适当的平面直角坐标系,描述物体的位置。
素养目标 1.理解平面直角坐标系以及横轴、纵轴、原点、坐标等概念。 2.认识并能画出平面直角坐标系。 3.能在给定的平面直角坐标系中,由点的位置写出它的坐标,由坐标可以找到相应的点。 4.了解在平面直角坐标系中,有序实数对与平面上的点是一一对应的。
教学重难点 重点:在给定的平面直角坐标系中,由点的位置写出它的坐标,由坐标可以找到相应的点。 难点:理解在平面直角坐标系中,有序实数对与平面上的点是一一对应的。
教学策略 学生已经学习了数轴,画平面直角坐标系时有一定的基础。在平面直角坐标系中描出已知坐标的点,或者读出已知点的坐标,学生对于这种类型掌握应该较好。但是对于平面直角坐标系中,有序实数对与平面上的点的一一对应关系,学生理解不好。针对以上问题解决的策略是应加强学生有效信息获取能力的培养,通过类比所举例子,进一步加深学生对一一对应的理解。
温故知新 问题1:什么是数轴 问题2:数轴的三要素是什么 问题3:数轴上点A和点B表示的数是多少 数轴上的点和实数有怎样的关系
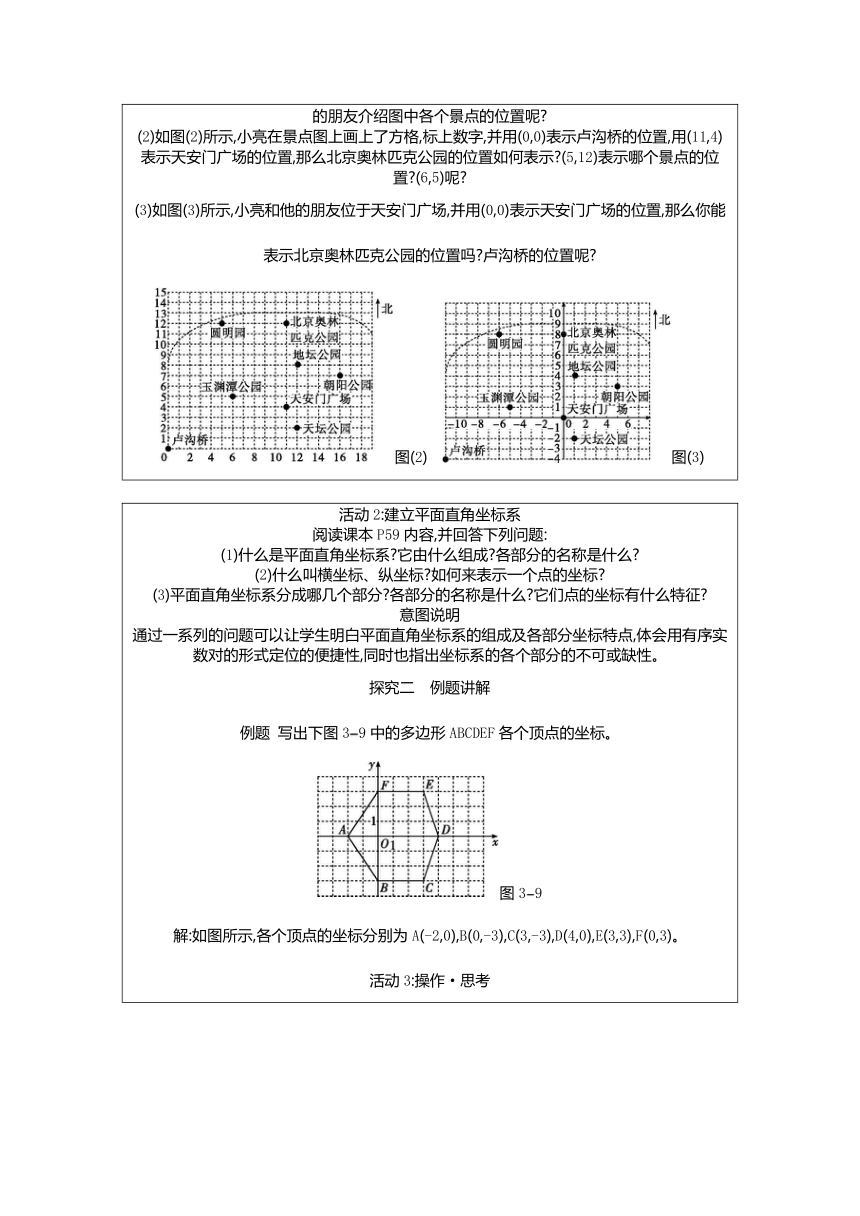
新知初探 探究一 平面直角坐标系 图(1) 活动1:认识平面直角坐标系 (1)图(1)呈现了北京市部分景点的大致位置,小亮和来访的朋友位于卢沟桥,小亮如何向来访的朋友介绍图中各个景点的位置呢 (2)如图(2)所示,小亮在景点图上画上了方格,标上数字,并用(0,0)表示卢沟桥的位置,用(11,4)表示天安门广场的位置,那么北京奥林匹克公园的位置如何表示 (5,12)表示哪个景点的位置 (6,5)呢 (3)如图(3)所示,小亮和他的朋友位于天安门广场,并用(0,0)表示天安门广场的位置,那么你能表示北京奥林匹克公园的位置吗 卢沟桥的位置呢 图(2) 图(3)
活动2:建立平面直角坐标系 阅读课本P59内容,并回答下列问题: (1)什么是平面直角坐标系 它由什么组成 各部分的名称是什么 (2)什么叫横坐标、纵坐标 如何来表示一个点的坐标 (3)平面直角坐标系分成哪几个部分 各部分的名称是什么 它们点的坐标有什么特征 意图说明 通过一系列的问题可以让学生明白平面直角坐标系的组成及各部分坐标特点,体会用有序实数对的形式定位的便捷性,同时也指出坐标系的各个部分的不可或缺性。 探究二 例题讲解 例题 写出下图39中的多边形ABCDEF各个顶点的坐标。 图39 解:如图所示,各个顶点的坐标分别为A(-2,0),B(0,-3),C(3,-3),D(4,0),E(3,3),F(0,3)。 活动3:操作·思考 图310 (1)在图310所示的平面直角坐标系中,描出下列各点:A(-5,0),B(1,4),C(3,3),D(1,0),E(3,-3),F(1,-4)。 (2)依次连接A,B,C,D,E,F,A,你得到什么图形 (3)在平面直角坐标系中,点与有序实数对之间有何关系 解:依次连接A,B,C,D,E,F,A,可得如图所示图形。 归纳总结:在平面直角坐标系中,对于平面上的任意一点,都有唯一的一个有序实数对(即点的坐标)与它对应;反过来,对于任意一个有序实数对,都有平面上唯一的一点和它对应。 意图说明 通过探究活动,增加对坐标系、象限和坐标点的深入理解,并认识到坐标与点的一一对应关系。
当堂达标
课堂小结
板书设计 平面直角坐标系的有关概念 1.平面直角坐标系相关概念
(1)横轴
(2)纵轴
(3)原点
(4)象限
(5)坐标 2.例题讲解
教学反思
课标摘录 1.理解平面直角坐标系的有关概念,能画出平面直角坐标系;在给定的平面直角坐标系中,能根据坐标描出点的位置,由点的位置写出坐标。 2.在实际问题中,能建立适当的平面直角坐标系,描述物体的位置。
素养目标 1.理解平面直角坐标系以及横轴、纵轴、原点、坐标等概念。 2.认识并能画出平面直角坐标系。 3.能在给定的平面直角坐标系中,由点的位置写出它的坐标,由坐标可以找到相应的点。 4.了解在平面直角坐标系中,有序实数对与平面上的点是一一对应的。
教学重难点 重点:在给定的平面直角坐标系中,由点的位置写出它的坐标,由坐标可以找到相应的点。 难点:理解在平面直角坐标系中,有序实数对与平面上的点是一一对应的。
教学策略 学生已经学习了数轴,画平面直角坐标系时有一定的基础。在平面直角坐标系中描出已知坐标的点,或者读出已知点的坐标,学生对于这种类型掌握应该较好。但是对于平面直角坐标系中,有序实数对与平面上的点的一一对应关系,学生理解不好。针对以上问题解决的策略是应加强学生有效信息获取能力的培养,通过类比所举例子,进一步加深学生对一一对应的理解。
温故知新 问题1:什么是数轴 问题2:数轴的三要素是什么 问题3:数轴上点A和点B表示的数是多少 数轴上的点和实数有怎样的关系
新知初探 探究一 平面直角坐标系 图(1) 活动1:认识平面直角坐标系 (1)图(1)呈现了北京市部分景点的大致位置,小亮和来访的朋友位于卢沟桥,小亮如何向来访的朋友介绍图中各个景点的位置呢 (2)如图(2)所示,小亮在景点图上画上了方格,标上数字,并用(0,0)表示卢沟桥的位置,用(11,4)表示天安门广场的位置,那么北京奥林匹克公园的位置如何表示 (5,12)表示哪个景点的位置 (6,5)呢 (3)如图(3)所示,小亮和他的朋友位于天安门广场,并用(0,0)表示天安门广场的位置,那么你能表示北京奥林匹克公园的位置吗 卢沟桥的位置呢 图(2) 图(3)
活动2:建立平面直角坐标系 阅读课本P59内容,并回答下列问题: (1)什么是平面直角坐标系 它由什么组成 各部分的名称是什么 (2)什么叫横坐标、纵坐标 如何来表示一个点的坐标 (3)平面直角坐标系分成哪几个部分 各部分的名称是什么 它们点的坐标有什么特征 意图说明 通过一系列的问题可以让学生明白平面直角坐标系的组成及各部分坐标特点,体会用有序实数对的形式定位的便捷性,同时也指出坐标系的各个部分的不可或缺性。 探究二 例题讲解 例题 写出下图39中的多边形ABCDEF各个顶点的坐标。 图39 解:如图所示,各个顶点的坐标分别为A(-2,0),B(0,-3),C(3,-3),D(4,0),E(3,3),F(0,3)。 活动3:操作·思考 图310 (1)在图310所示的平面直角坐标系中,描出下列各点:A(-5,0),B(1,4),C(3,3),D(1,0),E(3,-3),F(1,-4)。 (2)依次连接A,B,C,D,E,F,A,你得到什么图形 (3)在平面直角坐标系中,点与有序实数对之间有何关系 解:依次连接A,B,C,D,E,F,A,可得如图所示图形。 归纳总结:在平面直角坐标系中,对于平面上的任意一点,都有唯一的一个有序实数对(即点的坐标)与它对应;反过来,对于任意一个有序实数对,都有平面上唯一的一点和它对应。 意图说明 通过探究活动,增加对坐标系、象限和坐标点的深入理解,并认识到坐标与点的一一对应关系。
当堂达标
课堂小结
板书设计 平面直角坐标系的有关概念 1.平面直角坐标系相关概念
(1)横轴
(2)纵轴
(3)原点
(4)象限
(5)坐标 2.例题讲解
教学反思
同课章节目录
