4.4 第3课时借助两个一次函数图象解决实际问题 教案(表格式) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 4.4 第3课时借助两个一次函数图象解决实际问题 教案(表格式) 2025-2026学年数学北师大版(2024)八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 155.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-04 00:00:00 | ||
图片预览


文档简介
第3课时 借助两个一次函数图象解决实际问题
课标摘录 1.结合具体情境体会一次函数的意义,能根据已知条件确定一次函数的表达式;会运用待定系数法确定一次函数的表达式。 2.能用一次函数解决简单实际问题。
素养目标 1.通过观察函数图象,能够从同一坐标系中的两个一次函数图象中获取信息,理解两个一次函数图象交点的实际意义。 2.利用函数图象,解决实际问题。 3.会建立函数的数学模型,解决较深层次的实际问题。
教学重难点 重点:利用在同一平面直角坐标系中的两个一次函数图象解决实际问题。 难点:1.从函数的图象中提炼出有用的信息。 2.对在同一平面直角坐标系中的两个一次函数图象交点的理解。
教学策略 在课堂教学中对于例题采用教师提出问题,学生讨论,学生回答,教师修正,板书的形式。采用学生自主学习与合作学习相结合的方式,以学生讨论,互帮互助为主,教师指导为辅,给学生充分的讨论和考虑时间。
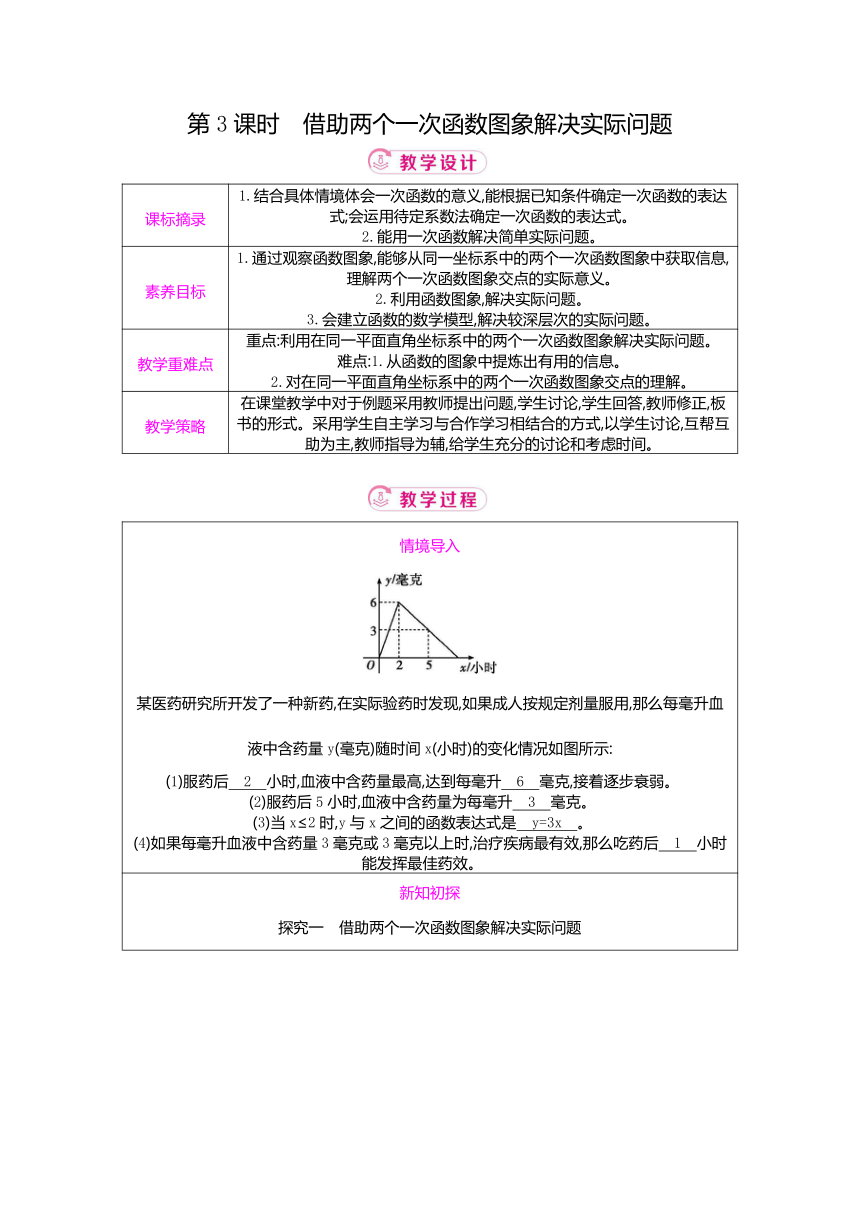
情境导入 某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(小时)的变化情况如图所示: (1)服药后 2 小时,血液中含药量最高,达到每毫升 6 毫克,接着逐步衰弱。 (2)服药后5小时,血液中含药量为每毫升 3 毫克。 (3)当x≤2时,y与x之间的函数表达式是 y=3x 。 (4)如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,那么吃药后 1 小时能发挥最佳药效。
新知初探 探究一 借助两个一次函数图象解决实际问题 活动1:如图所示,l1表示某公司产品的销售收入与销售量之间的关系,l2表示该公司产品的销售成本与销售量之间的关系,根据图象填空。 (1)当销售量为2 t时,销售收入= 2 000 元,销售成本= 3 000 元。 (2)当销售量为6 t时,销售收入= 6 000 元,销售成本= 5 000 元。 (3)当销售量为 4 t 时,销售收入等于销售成本。 (4)当销售量 大于4 t 时,该公司赢利(收入大于成本);当销售量 小于4 t 时,该公司亏损(收入小于成本)。 (5)当销售量等于 6 t 时,该公司赢利(收入减成本)1 000元。 (6)l1对应的函数表达式是 y=1 000x ,l2对应的函数表达式是 y=500x+2 000 。 (7)你能借助(6)的结论求解(5)吗 1 000x-(500x+2 000)=1 000,解得x=6。当销售量等于 6 t时,该公司赢利1 000元。 活动2:思考·交流 上题中,l1对应的一次函数y=k1x+b1,k1和b1的实际意义各是什么 设l2对应的一次函数y=k2x+b2,k2和b2的实际意义各是什么 解:l1中,k1=1 000,b1=0,k1表示的是每销售1吨,销售收入是1 000元,b1表示未销售时,销售收入为0;l2中,k2=500,b2=2 000,k2表示的是销售量每增加1吨,销售成本增加500元,b2表示未销售时,销售所花的成本是2 000元。
意图说明 此探究活动培养了学生的识图能力和探究能力,调动学生学习的自主意识。通过问题串的精心设计,引导学生根据实际问题建立适当的函数模型,利用该函数图象的特征解决这个问题。在此过程中渗透了数形结合的思想,同时发展学生的数学应用能力。 探究二 例题讲解 例题 图411是某景区游览路线示意图。甲在观景台1联系乙,发现乙在观景台2,于是沿着游览路线追赶乙。图412中l1,l2分别表示甲、乙两人到观景台1的路程s(单位:m)与追赶时间t(单位:min)之间的关系。 图411 图412 假设甲、乙两人保持现有的速度,根据图象回答下列问题: (1)哪条线表示甲到观景台1的路程与追赶时间之间的关系 (2)甲和乙哪个人的速度快 (3)30 min内甲能否追上乙 (4)到达观景台3后道路分岔,甲能否在到达观景台3前追上乙 (5)设l1与l2对应的两个一次函数分别为s=k1t+b1与s=k2t+b2,k1,k2的实际意义各是什么 甲、乙两人的速度各是多少 解:(1)当t=0时,甲到观景台1的路程为0 m,即s=0,故l1表示甲到观景台1的路程与追赶时间之间的关系。 (2)t从0增加到20时,l1上点的纵坐标增加了1 000,l2上点的纵坐标增加了600,即20 min内,甲行走了1 000 m,乙行走了600 m,所以甲的速度快。 (3)如图413所示,延长l1,l2,可以看出,当t=30时,l1上的对应点在l2上对应点的下方,这表明,30 min时甲尚未追上乙。 (4)在图413中,l1与l2交点P的纵坐标小于(800+1 300=)2 100,这说明,甲能在到达观景台3前追上乙。 (5)k1表示甲的速度,k2表示乙的速度。甲的速度是50 m/min,乙的速度是30 m/min。 意图说明 进一步培养学生的识图能力和探究能力,调动学生学习的自主意识,通过问题串的精心设计,引导学生根据实际问题建立适当的函数模型,利用该函数图象的特征解决这个问题。在此过程中渗透数形结合的思想方法,发展学生的数学应用能力,加强学生运用一次函数的图象分析、解决问题的能力,鼓励学生运用多种方法解决问题,提高学生的解题能力。
当堂达标
课堂小结
板书设计 借助两个一次函数图象解决实际问题 1.横轴、纵轴表示的意义 2.直线与坐标轴的交点表示的意义 3.理解表达式中k,b的实际意义
教学反思
课标摘录 1.结合具体情境体会一次函数的意义,能根据已知条件确定一次函数的表达式;会运用待定系数法确定一次函数的表达式。 2.能用一次函数解决简单实际问题。
素养目标 1.通过观察函数图象,能够从同一坐标系中的两个一次函数图象中获取信息,理解两个一次函数图象交点的实际意义。 2.利用函数图象,解决实际问题。 3.会建立函数的数学模型,解决较深层次的实际问题。
教学重难点 重点:利用在同一平面直角坐标系中的两个一次函数图象解决实际问题。 难点:1.从函数的图象中提炼出有用的信息。 2.对在同一平面直角坐标系中的两个一次函数图象交点的理解。
教学策略 在课堂教学中对于例题采用教师提出问题,学生讨论,学生回答,教师修正,板书的形式。采用学生自主学习与合作学习相结合的方式,以学生讨论,互帮互助为主,教师指导为辅,给学生充分的讨论和考虑时间。
情境导入 某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(小时)的变化情况如图所示: (1)服药后 2 小时,血液中含药量最高,达到每毫升 6 毫克,接着逐步衰弱。 (2)服药后5小时,血液中含药量为每毫升 3 毫克。 (3)当x≤2时,y与x之间的函数表达式是 y=3x 。 (4)如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,那么吃药后 1 小时能发挥最佳药效。
新知初探 探究一 借助两个一次函数图象解决实际问题 活动1:如图所示,l1表示某公司产品的销售收入与销售量之间的关系,l2表示该公司产品的销售成本与销售量之间的关系,根据图象填空。 (1)当销售量为2 t时,销售收入= 2 000 元,销售成本= 3 000 元。 (2)当销售量为6 t时,销售收入= 6 000 元,销售成本= 5 000 元。 (3)当销售量为 4 t 时,销售收入等于销售成本。 (4)当销售量 大于4 t 时,该公司赢利(收入大于成本);当销售量 小于4 t 时,该公司亏损(收入小于成本)。 (5)当销售量等于 6 t 时,该公司赢利(收入减成本)1 000元。 (6)l1对应的函数表达式是 y=1 000x ,l2对应的函数表达式是 y=500x+2 000 。 (7)你能借助(6)的结论求解(5)吗 1 000x-(500x+2 000)=1 000,解得x=6。当销售量等于 6 t时,该公司赢利1 000元。 活动2:思考·交流 上题中,l1对应的一次函数y=k1x+b1,k1和b1的实际意义各是什么 设l2对应的一次函数y=k2x+b2,k2和b2的实际意义各是什么 解:l1中,k1=1 000,b1=0,k1表示的是每销售1吨,销售收入是1 000元,b1表示未销售时,销售收入为0;l2中,k2=500,b2=2 000,k2表示的是销售量每增加1吨,销售成本增加500元,b2表示未销售时,销售所花的成本是2 000元。
意图说明 此探究活动培养了学生的识图能力和探究能力,调动学生学习的自主意识。通过问题串的精心设计,引导学生根据实际问题建立适当的函数模型,利用该函数图象的特征解决这个问题。在此过程中渗透了数形结合的思想,同时发展学生的数学应用能力。 探究二 例题讲解 例题 图411是某景区游览路线示意图。甲在观景台1联系乙,发现乙在观景台2,于是沿着游览路线追赶乙。图412中l1,l2分别表示甲、乙两人到观景台1的路程s(单位:m)与追赶时间t(单位:min)之间的关系。 图411 图412 假设甲、乙两人保持现有的速度,根据图象回答下列问题: (1)哪条线表示甲到观景台1的路程与追赶时间之间的关系 (2)甲和乙哪个人的速度快 (3)30 min内甲能否追上乙 (4)到达观景台3后道路分岔,甲能否在到达观景台3前追上乙 (5)设l1与l2对应的两个一次函数分别为s=k1t+b1与s=k2t+b2,k1,k2的实际意义各是什么 甲、乙两人的速度各是多少 解:(1)当t=0时,甲到观景台1的路程为0 m,即s=0,故l1表示甲到观景台1的路程与追赶时间之间的关系。 (2)t从0增加到20时,l1上点的纵坐标增加了1 000,l2上点的纵坐标增加了600,即20 min内,甲行走了1 000 m,乙行走了600 m,所以甲的速度快。 (3)如图413所示,延长l1,l2,可以看出,当t=30时,l1上的对应点在l2上对应点的下方,这表明,30 min时甲尚未追上乙。 (4)在图413中,l1与l2交点P的纵坐标小于(800+1 300=)2 100,这说明,甲能在到达观景台3前追上乙。 (5)k1表示甲的速度,k2表示乙的速度。甲的速度是50 m/min,乙的速度是30 m/min。 意图说明 进一步培养学生的识图能力和探究能力,调动学生学习的自主意识,通过问题串的精心设计,引导学生根据实际问题建立适当的函数模型,利用该函数图象的特征解决这个问题。在此过程中渗透数形结合的思想方法,发展学生的数学应用能力,加强学生运用一次函数的图象分析、解决问题的能力,鼓励学生运用多种方法解决问题,提高学生的解题能力。
当堂达标
课堂小结
板书设计 借助两个一次函数图象解决实际问题 1.横轴、纵轴表示的意义 2.直线与坐标轴的交点表示的意义 3.理解表达式中k,b的实际意义
教学反思
同课章节目录
