第1章直角三角形单元试卷（含答案）

初中数学湘教版八年级下册：第1章
直角三角形
一、选择题（共10小题；共50分）
1.
如图，在四边形
中，，
和
的延长线交于点
，若点
使得
，则满足此条件的点
(
)
A.
有且只有
个
B.
有且只有
个
C.
组成
的角平分线
D.
组成
的角平分线所在的直线（
点除外）
2.
如图，在
中，，，，过点
作
，垂足为
，则
的长为 (
)
A.
B.
C.
D.
3.
如图，在
中，，，边
的垂直平分线
交
于点
，交
于点
，，则
的长为 (
)
A.
B.
C.
D.
4.
如图所示的正方形网格中，网格线的交点称为格点．已知
，
是两格点，如果
也是图中的格点，且使得
为等腰三角形，则点
的个数是 (
)
A.
B.
C.
D.
5.
下列每一组数据中的三个数值分别为三角形的三边长，不能构成直角三角形的是
A.
，，
B.
，，
C.
，，
D.
，，
6.
如图，已知点
和点
，在坐标轴上确定点
，使得
为直角三角形，则满足这样条件的点
共有 (
)
A.
个
B.
个
C.
个
D.
个
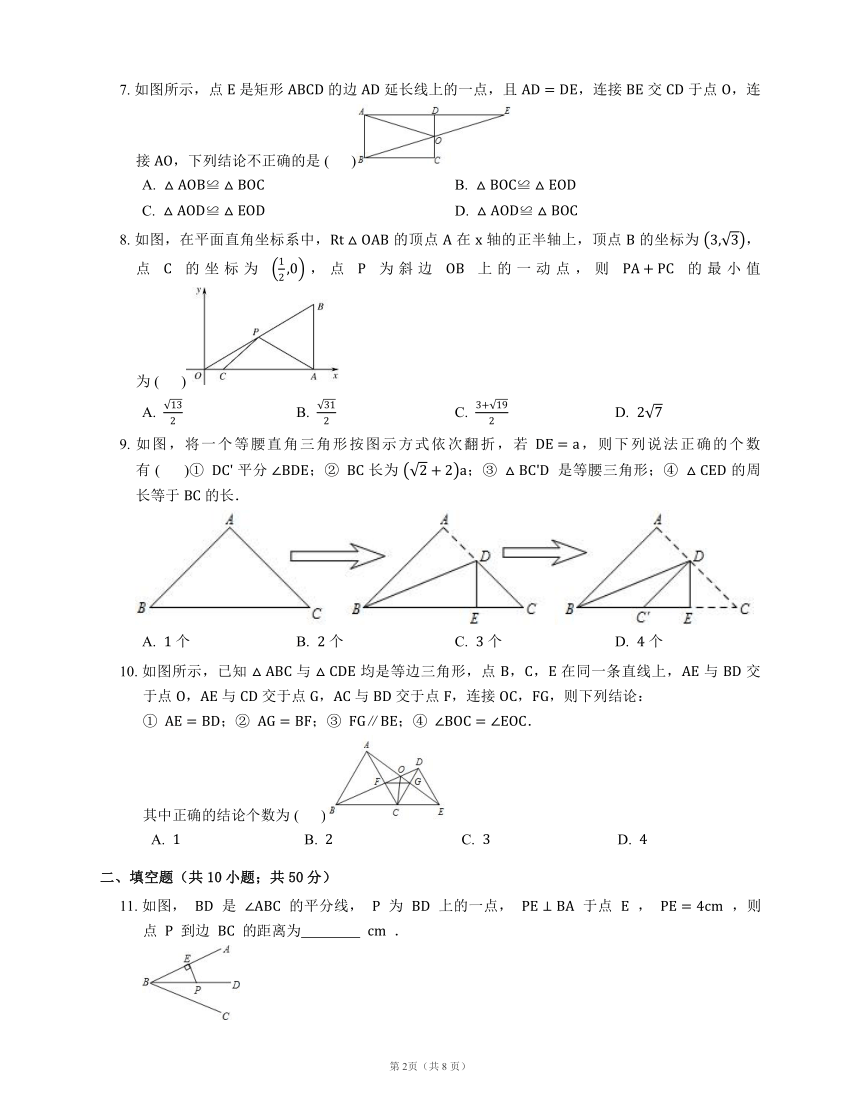
7.
如图所示，点
是矩形
的边
延长线上的一点，且
，连接
交
于点
，连接
，下列结论不正确的是 (
)
A.
B.
C.
D.
8.
如图，在平面直角坐标系中，
的顶点
在
轴的正半轴上，顶点
的坐标为
，点
的坐标为
，点
为斜边
上的一动点，则
的最小值为 (
)
A.
B.
C.
D.
9.
如图，将一个等腰直角三角形按图示方式依次翻折，若
，则下列说法正确的个数有 (
)①
平分
；②
长为
；③
是等腰三角形；④
的周长等于
的长．
A.
个
B.
个
C.
个
D.
个
10.
如图所示，已知
与
均是等边三角形，点
，，
在同一条直线上，
与
交于点
，
与
交于点
，
与
交于点
，连接
，，则下列结论：
①
；②
；③
；④
．
其中正确的结论个数为 (
)
A.
B.
C.
D.
二、填空题（共10小题；共50分）
11.
如图，
是
的平分线，
为
上的一点，
于点
，
，则点
到边
的距离为

．
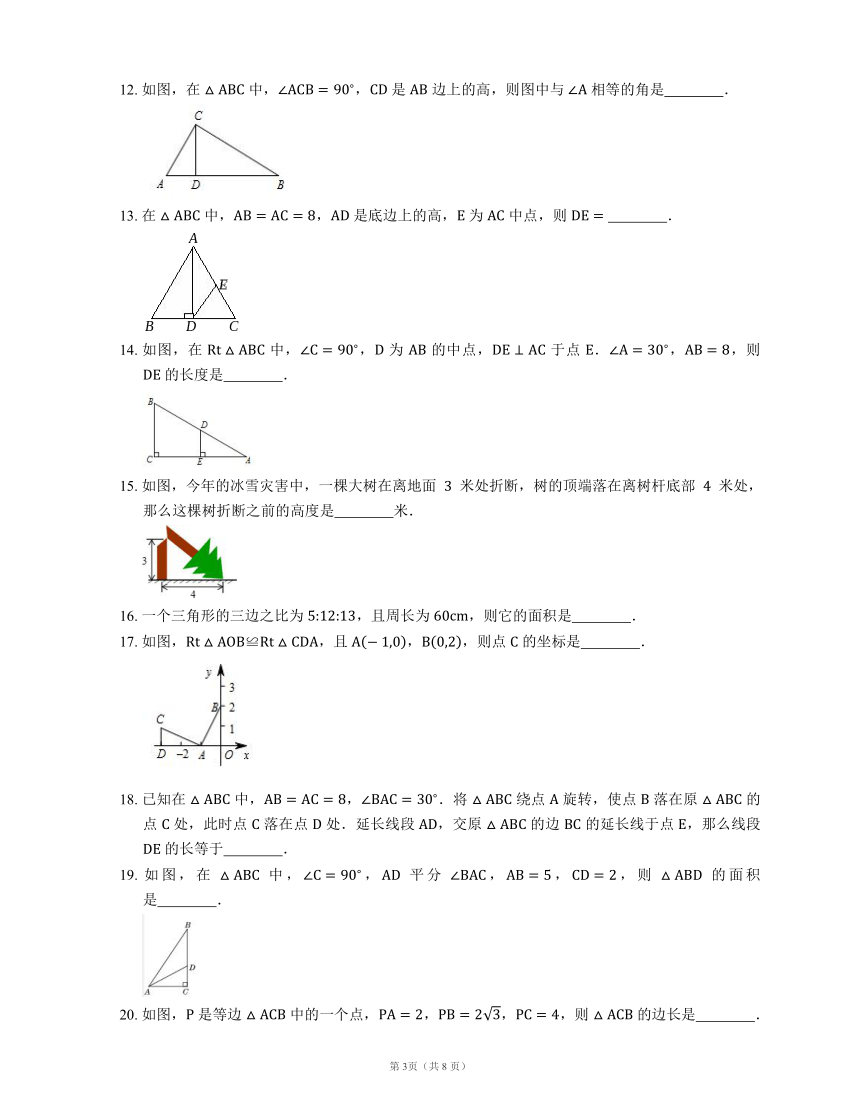
12.
如图，在
中，，
是
边上的高，则图中与
相等的角是
．
13.
在
中，，
是底边上的高，
为
中点，则
．
14.
如图，在
中，，
为
的中点，
于点
．，，则
的长度是
．
15.
如图，今年的冰雪灾害中，一棵大树在离地面
米处折断，树的顶端落在离树杆底部
米处，那么这棵树折断之前的高度是
米．
16.
一个三角形的三边之比为
，且周长为
，则它的面积是
．
17.
如图，，且
，，则点
的坐标是
．
18.
已知在
中，，．将
绕点
旋转，使点
落在原
的点
处，此时点
落在点
处．延长线段
，交原
的边
的延长线于点
，那么线段
的长等于
．
19.
如图，在
中，，
平分
，，，则
的面积是
．
20.
如图，
是等边
中的一个点，，，，则
的边长是
．
三、解答题（共5小题；共65分）
21.
已知在
中，
的平分线
与
的垂直平分线
交于点
，
与
，
交
的延长线于
，你认为
与
之间有什么关系 试证明你的发现．
22.
如图，在
中，，
是
上一点，且
．求证：．
23.
如图，在
中，
于点
，
于点
，
为
的中点．
（1）
若
，，求
的周长；
（2）
若
，，求
的度数．
24.
如图，有两条公路
，
相交成
角，沿公路
方向离
点
米处有一所学校
．当重型运输卡车
沿道路
方向行驶时，在以
为圆心
米长为半径的圆形区域内都会受到卡车噪声的影响，且卡车
与学校
的距离越近噪声影响越大．若一直重型运输卡车
沿道路
方向行驶的速度为
千米/时．
（1）
求对学校
的噪声影响最大时卡车
与学校
的距离；
（2）
求卡车
沿道路
方向行驶一次给学校
带来噪声影响的时间．
25.
已知某开发区有一块四边形空地
，如图所示，现计划在空地上种植草皮，经测量
，，，，，若每平方米草皮需要
元，求一共需要投入多少元．
答案
第一部分
1.
D
2.
C
3.
C
4.
C
5.
C
6.
C
7.
A
8.
B
9.
C
10.
D
第二部分
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
第三部分
21.
结论：．
连接
，
．
平分
，，，
，
垂直平分
，
，
在
与
中
，
．
22.
，
．
，
．
．
．
23.
（1）
，，
为
的中点，
．
，，
的周长
．
（2）
，
，
．
，
．
．
．
24.
（1）
过点
作
于点
，
，，
，
即对学校
的噪声影响最大时卡车
与学校
的距离为
米．
（2）
如图：
在
中，，，由勾股定理得
，
故
米，即重型运输卡车在经过
时对学校产生影响．
重型运输卡车的速度为
千米/小时，即
米/分钟，
重型运输卡车经过
时需要
（分钟）．
答：卡车
沿道路
方向行驶一次给学校
带来噪声影响的时间为
分钟．
25.
连接
，
在
中
，，，
利用勾股定理解得
．
在
中，
，，，
根据勾股定理的逆定理得
．
．
．
四边形
的面积是
．
每平方米草皮需要
元，
元．
第1页（共1
页）