2.4.1 直线与圆锥曲线的交点(教学课件)__高二数学北师大(2019)选择性必修第一册(共31页PPT)
文档属性
| 名称 | 2.4.1 直线与圆锥曲线的交点(教学课件)__高二数学北师大(2019)选择性必修第一册(共31页PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-04 23:10:07 | ||
图片预览










文档简介
(共31张PPT)
2.4.1 直线与圆锥曲线的交点
学习目标
1.会求直线与圆锥曲线的交点坐标,体现数学运算能力(重点)
2.利用直线与圆锥曲线的方程会判断直线与圆锥曲线的交点个数,会由直线与圆锥曲线的交点个数,求参数的范围,体现逻辑推理和数学运算能力(重难点)
新课导入
前面我们已经学习了直线以及圆、椭圆、双曲线、抛物线等一系列的特殊曲线,通过平面直角坐标系,把圆锥曲线上的点和相应的圆锥曲线方程的解建立了一一对应的关系,判定直线与圆锥曲线交点的个数.可以通过作出图象来确定.那么,我们是否还可以通过方程组的解的个数判定两者的交点个数呢?
这节课来学习一下.
新课学习
思考一下:如何判断直线与圆的位置关系?
几何法:利用圆心到直线的距离d与半径r之间的关系判断
代数法:联立得到方程组
消元化简得到一个关于x或y的一元二次方程.
新课学习
思考一下:对于椭圆这个封闭图形而言,类比直线与圆的位置关系,直线与椭圆存在怎样的位置关系呢?
联立直线与椭圆方程
消去y得一个关于x的一元二次方程: (b2+a2k2)x2+2kma2x+a2(m2-b2)=0
Δ的取值 解的个数 位置关系
Δ>0
Δ=0
Δ<0
两解
一解
相切
相离
相交
新课学习
思考一下:如何判定直线与双曲线的位置关系?
把直线与双曲线的方程联立成方程组,通过消元后化为ax2+bx+c=0的形式,在a≠0的情况下考察方程的判别式.
(1) Δ>0时,直线与双曲线有两个不同的公共点;
Δ=0时,直线与双曲线只有一个公共点;
Δ<0时,直线与双曲线没有公共点.
(2)当a=0时,此时直线与双曲线的渐近线平行,直线与双曲线有一个公共点.
新课学习
思考一下:如何判定直线与抛物线的位置关系?
设直线l:y=kx+m,抛物线:y2=2px(p>0),将直线方程与抛物线方程联立整理成关于x的方程k2x2+2(km-p)x+m2=0
(1)若k≠0时,当Δ>0时,直线与抛物线相交,有两个交点;
当Δ=0时,直线与抛物线相切,有一个交点;
当Δ<0时,直线与抛物线相离,没有公共点.
(2)若k=0时,直线与抛物线有一个交点,此时直线平行于抛物线的对称轴或与对称轴重合.
新课学习
拓展:直线与双曲线的位置关系的判断方法:
1.代数法
将直线方程与双曲线方程联立,方程组的解的组数就是直线与双曲线交点的个数.联立得方程组,消去x或y中的一个后,得到的形如二次方程的式子中,要注意x2项或y2项的系数是否为零,否则容易漏解.
2.数形结合法
判断直线与双曲线的交点情况时,可以根据双曲线的渐近线的斜率与直线的斜率的大小关系,确定直线与双曲线的位置关系.
新课学习
例1:如图,已知直线l:y=-x+1与椭圆C: ,判断直线与椭圆的位置关系,若相交,求出交点坐标.
直线l与椭圆C的交点坐标是方程组 的解
方程组可化为
①
②
将①代入②,得
x2+3(-x+1)2=3
化简,得,
2x2-3x=0
解得
x1=0,x2=
新课学习
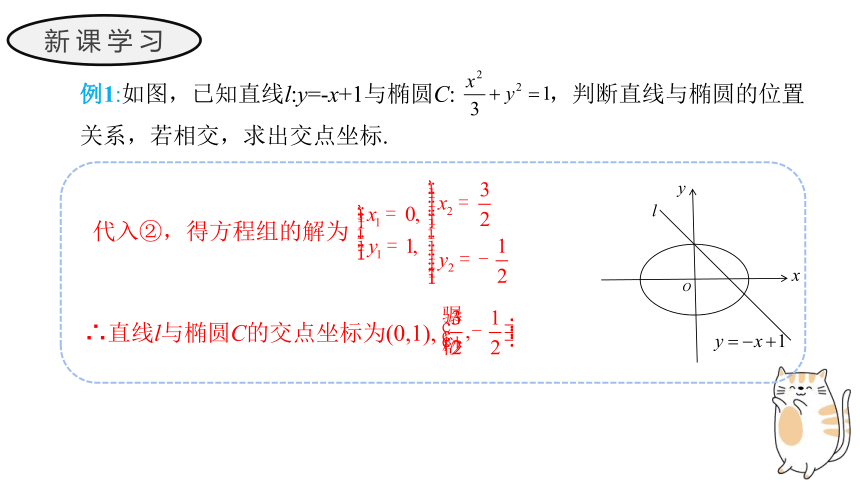
例1:如图,已知直线l:y=-x+1与椭圆C: ,判断直线与椭圆的位置关系,若相交,求出交点坐标.
代入②,得方程组的解为
∴直线l与椭圆C的交点坐标为(0,1),
新课学习
思考交流:在例1中,若仅需要判断直线l与椭圆C的交点个数,在不求出交点坐标的情况下,如何判断?理由是什么?
联立直线l与椭圆C的方程,消去y得一个关于x的一元二次方程,求一元二次方程的Δ,
若Δ>0时,直线与椭圆相交,有两个交点;
若Δ=0时,直线与椭圆相切,有一个交点;
若Δ<0时,直线与椭圆相离,没有交点.
新课学习
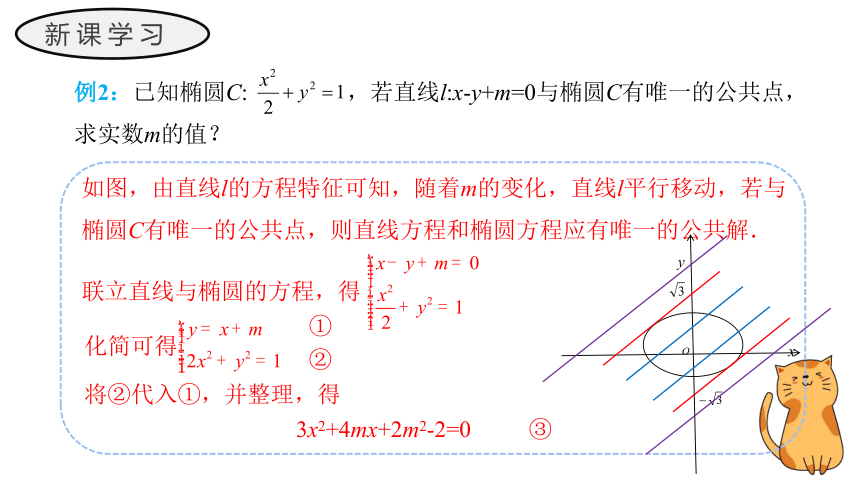
例2:已知椭圆C: ,若直线l:x-y+m=0与椭圆C有唯一的公共点,求实数m的值?
如图,由直线l的方程特征可知,随着m的变化,直线l平行移动,若与椭圆C有唯一的公共点,则直线方程和椭圆方程应有唯一的公共解.
联立直线与椭圆的方程,得
化简可得
①
②
将②代入①,并整理,得
3x2+4mx+2m2-2=0
③
新课学习
例2:已知椭圆C: ,若直线l:x-y+m=0与椭圆C有唯一的公共点,求实数m的值?
因为方程③是一元二次方程,所以它有唯一的实数解的充要条件是
Δ=16m2-24(m2-1)=0
解得m= 或m=
所以当直线l与椭圆C有唯一的公共点时,实数m的值为 或
新课学习
例3:已知直线l经过点A(0,1),且与抛物线 C:y=x2有唯一的公共点,求直线l的方程.
如图:
(1)当直线l的斜率不存在时,直线l:x=0(y轴)与抛物线C相切于原点,符合条件.
(2)当直线l的斜率存在时,设直线l的方程为y=kx+1.
由方程组
消去y并整理,得
k2x2+(2k-1)x+1=0 (*)
新课学习
例3:已知直线l经过点A(0,1),且与抛物线 C:y=x2有唯一的公共点,求直线l的方程.
①当k2=0时,直线l的方程为y=1,此时,方程组有唯一的实数解,符合条件;
②当k2≠0时,方程有唯一的实数解的充要条件是Δ=(2k2-1)2-4k2=0.
解得k= .此时,方程组有唯一的实数解,符合条件.
综上,满足题意的直线l有三条:x=0,y=1,y= x+1
新课学习
例4:讨论直线l:y=kx+1与双曲线C:x2-y2=1的公共点的个数.
联立方程组
消去y,整理得(1-k2)-2kx-2=0
(1)当k=1时,x=-1.
(2)当k=-1时,x=1.
(3)当k≠±1时,Δ=4k2+8(1-k2)=8-8k2.
若Δ>0,则 ;若Δ=0,则k=± ;若Δ<0,则 或 .
新课学习
例4:讨论直线l:y=kx+1与双曲线C:x2-y2=1的公共点的个数.
综上,当 或 时,直线l与双曲线C没有公共点;
当k=± 时,直线l与双曲线C相切于一点;
当k=±1时,直线l与双曲线C相交于一点;
当 或-1课堂巩固
C
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
A
课堂巩固
课堂巩固
(1,2)
课堂巩固
课堂总结
1.直线与椭圆的位置关系
2.直线与双曲线的位置关系
3.直线与抛物线的位置关系
THANK YOU
2.4.1 直线与圆锥曲线的交点
学习目标
1.会求直线与圆锥曲线的交点坐标,体现数学运算能力(重点)
2.利用直线与圆锥曲线的方程会判断直线与圆锥曲线的交点个数,会由直线与圆锥曲线的交点个数,求参数的范围,体现逻辑推理和数学运算能力(重难点)
新课导入
前面我们已经学习了直线以及圆、椭圆、双曲线、抛物线等一系列的特殊曲线,通过平面直角坐标系,把圆锥曲线上的点和相应的圆锥曲线方程的解建立了一一对应的关系,判定直线与圆锥曲线交点的个数.可以通过作出图象来确定.那么,我们是否还可以通过方程组的解的个数判定两者的交点个数呢?
这节课来学习一下.
新课学习
思考一下:如何判断直线与圆的位置关系?
几何法:利用圆心到直线的距离d与半径r之间的关系判断
代数法:联立得到方程组
消元化简得到一个关于x或y的一元二次方程.
新课学习
思考一下:对于椭圆这个封闭图形而言,类比直线与圆的位置关系,直线与椭圆存在怎样的位置关系呢?
联立直线与椭圆方程
消去y得一个关于x的一元二次方程: (b2+a2k2)x2+2kma2x+a2(m2-b2)=0
Δ的取值 解的个数 位置关系
Δ>0
Δ=0
Δ<0
两解
一解
相切
相离
相交
新课学习
思考一下:如何判定直线与双曲线的位置关系?
把直线与双曲线的方程联立成方程组,通过消元后化为ax2+bx+c=0的形式,在a≠0的情况下考察方程的判别式.
(1) Δ>0时,直线与双曲线有两个不同的公共点;
Δ=0时,直线与双曲线只有一个公共点;
Δ<0时,直线与双曲线没有公共点.
(2)当a=0时,此时直线与双曲线的渐近线平行,直线与双曲线有一个公共点.
新课学习
思考一下:如何判定直线与抛物线的位置关系?
设直线l:y=kx+m,抛物线:y2=2px(p>0),将直线方程与抛物线方程联立整理成关于x的方程k2x2+2(km-p)x+m2=0
(1)若k≠0时,当Δ>0时,直线与抛物线相交,有两个交点;
当Δ=0时,直线与抛物线相切,有一个交点;
当Δ<0时,直线与抛物线相离,没有公共点.
(2)若k=0时,直线与抛物线有一个交点,此时直线平行于抛物线的对称轴或与对称轴重合.
新课学习
拓展:直线与双曲线的位置关系的判断方法:
1.代数法
将直线方程与双曲线方程联立,方程组的解的组数就是直线与双曲线交点的个数.联立得方程组,消去x或y中的一个后,得到的形如二次方程的式子中,要注意x2项或y2项的系数是否为零,否则容易漏解.
2.数形结合法
判断直线与双曲线的交点情况时,可以根据双曲线的渐近线的斜率与直线的斜率的大小关系,确定直线与双曲线的位置关系.
新课学习
例1:如图,已知直线l:y=-x+1与椭圆C: ,判断直线与椭圆的位置关系,若相交,求出交点坐标.
直线l与椭圆C的交点坐标是方程组 的解
方程组可化为
①
②
将①代入②,得
x2+3(-x+1)2=3
化简,得,
2x2-3x=0
解得
x1=0,x2=
新课学习
例1:如图,已知直线l:y=-x+1与椭圆C: ,判断直线与椭圆的位置关系,若相交,求出交点坐标.
代入②,得方程组的解为
∴直线l与椭圆C的交点坐标为(0,1),
新课学习
思考交流:在例1中,若仅需要判断直线l与椭圆C的交点个数,在不求出交点坐标的情况下,如何判断?理由是什么?
联立直线l与椭圆C的方程,消去y得一个关于x的一元二次方程,求一元二次方程的Δ,
若Δ>0时,直线与椭圆相交,有两个交点;
若Δ=0时,直线与椭圆相切,有一个交点;
若Δ<0时,直线与椭圆相离,没有交点.
新课学习
例2:已知椭圆C: ,若直线l:x-y+m=0与椭圆C有唯一的公共点,求实数m的值?
如图,由直线l的方程特征可知,随着m的变化,直线l平行移动,若与椭圆C有唯一的公共点,则直线方程和椭圆方程应有唯一的公共解.
联立直线与椭圆的方程,得
化简可得
①
②
将②代入①,并整理,得
3x2+4mx+2m2-2=0
③
新课学习
例2:已知椭圆C: ,若直线l:x-y+m=0与椭圆C有唯一的公共点,求实数m的值?
因为方程③是一元二次方程,所以它有唯一的实数解的充要条件是
Δ=16m2-24(m2-1)=0
解得m= 或m=
所以当直线l与椭圆C有唯一的公共点时,实数m的值为 或
新课学习
例3:已知直线l经过点A(0,1),且与抛物线 C:y=x2有唯一的公共点,求直线l的方程.
如图:
(1)当直线l的斜率不存在时,直线l:x=0(y轴)与抛物线C相切于原点,符合条件.
(2)当直线l的斜率存在时,设直线l的方程为y=kx+1.
由方程组
消去y并整理,得
k2x2+(2k-1)x+1=0 (*)
新课学习
例3:已知直线l经过点A(0,1),且与抛物线 C:y=x2有唯一的公共点,求直线l的方程.
①当k2=0时,直线l的方程为y=1,此时,方程组有唯一的实数解,符合条件;
②当k2≠0时,方程有唯一的实数解的充要条件是Δ=(2k2-1)2-4k2=0.
解得k= .此时,方程组有唯一的实数解,符合条件.
综上,满足题意的直线l有三条:x=0,y=1,y= x+1
新课学习
例4:讨论直线l:y=kx+1与双曲线C:x2-y2=1的公共点的个数.
联立方程组
消去y,整理得(1-k2)-2kx-2=0
(1)当k=1时,x=-1.
(2)当k=-1时,x=1.
(3)当k≠±1时,Δ=4k2+8(1-k2)=8-8k2.
若Δ>0,则 ;若Δ=0,则k=± ;若Δ<0,则 或 .
新课学习
例4:讨论直线l:y=kx+1与双曲线C:x2-y2=1的公共点的个数.
综上,当 或 时,直线l与双曲线C没有公共点;
当k=± 时,直线l与双曲线C相切于一点;
当k=±1时,直线l与双曲线C相交于一点;
当 或-1
C
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
C
课堂巩固
课堂巩固
A
课堂巩固
课堂巩固
(1,2)
课堂巩固
课堂总结
1.直线与椭圆的位置关系
2.直线与双曲线的位置关系
3.直线与抛物线的位置关系
THANK YOU
同课章节目录
