5.2运动想象暑假预习练(含解析) 苏科版数学七年级上册
文档属性
| 名称 | 5.2运动想象暑假预习练(含解析) 苏科版数学七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 934.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-04 19:12:13 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
5.2运动想象
学校:___________姓名:___________班级:___________考号:___________
一、单选题
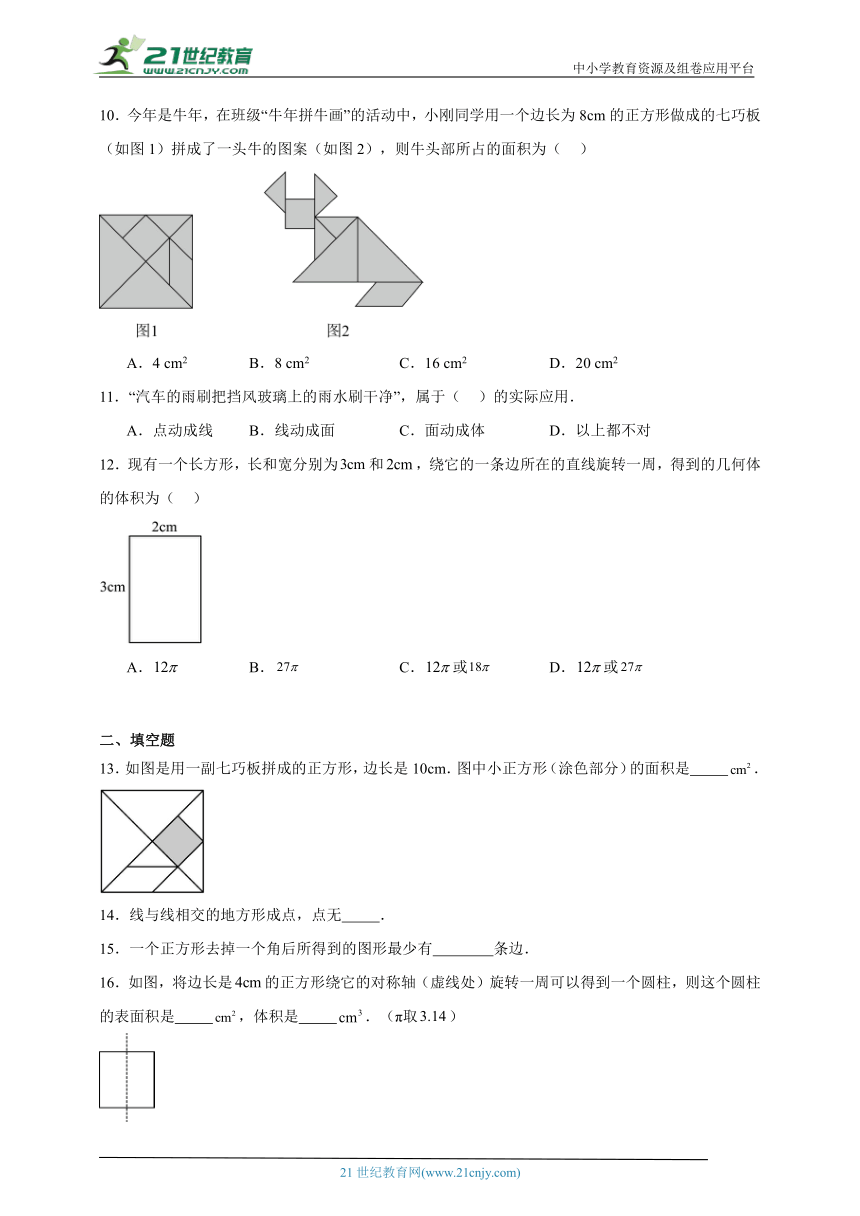
1.下列图形中,属于平面图形的是( )
A.长方体 B.圆锥体 C.圆柱 D.圆
2.“笔尖在纸上快速滑动写出数字9”运用数学知识解释这一现象为( )
A.点动成线 B.线动成面
C.面动成体 D.面与面相交得线
3.如图,绕虚线旋转一周可以得到的立体图形是( )
A. B. C. D.
4.将如图所示的平面图形绕直线旋转一周,可得到的立体图形是( )
A. B.
C. D.
5.如图,在直角三角形中,,,以直角边为轴旋转后得到的是( )
A.底面半径是8cm,高是6cm的圆锥 B.底面直径是8cm,高是6cm的圆锥
C.底面半径是6cm,高是8cm的圆锥 D.底面直径是6cm,高是8cm的圆锥
6.转动自行车的轮子,轮子上的辐条会形成一个圆面,用数学知识可以解释为( )
A.点动成线 B.线动成面 C.面动成体 D.面与面相交成线
7.一根彩绳和A、B、C三个钉子围成如图的三角形,如果将三角形的一个角顶点处的钉子去掉,并将这条彩绳钉成一个长方形, 则所钉成的长方形的面积是( )
A.7或15 B.16或15 C.7或15或16 D.无数个答案
8.如图,用对角线长为4的正方形,做了一套七巧板,拼成如图所示的一座桥,则桥中阴影部分的面积为( )
A.2 B.4 C.6 D.8
9.下图中的几何体(圆锥)是由下列( )平面图形绕轴旋转一周得到的.
A. B. C. D.
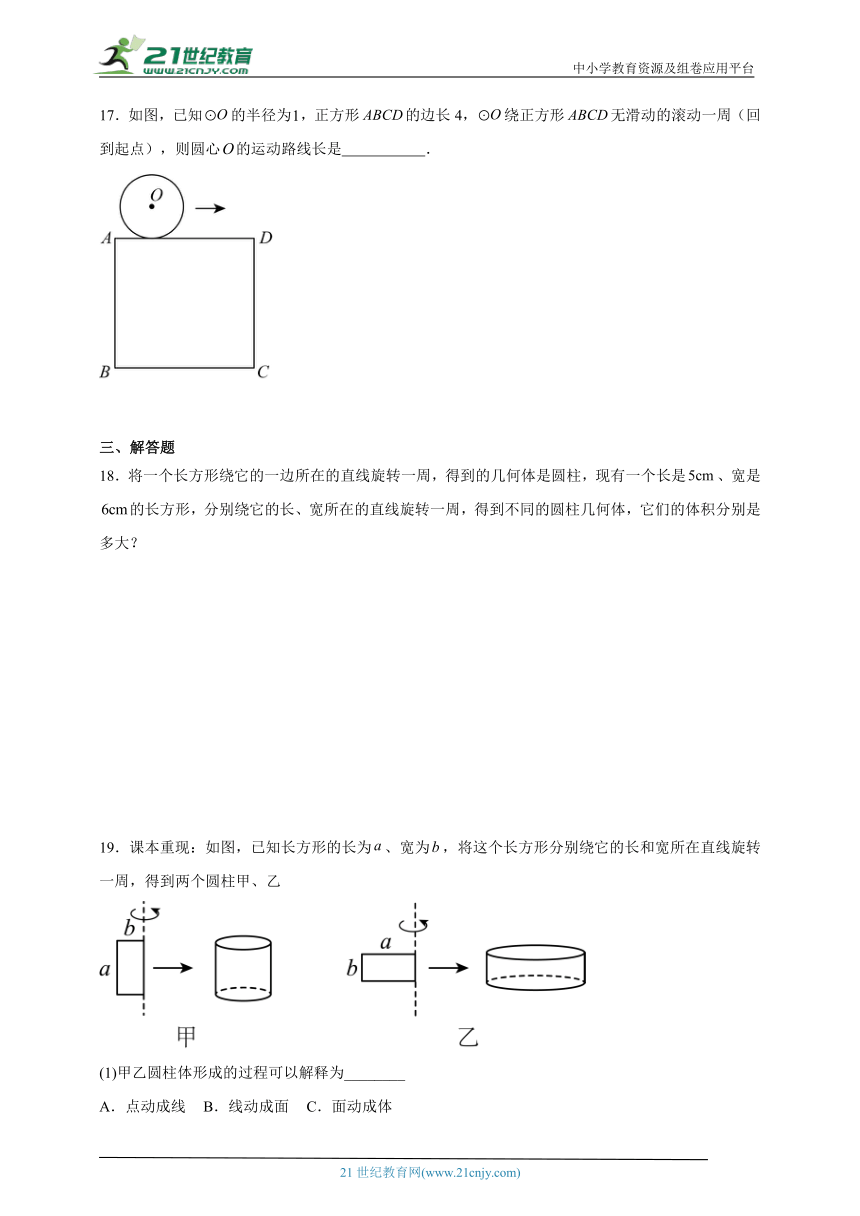
10.今年是牛年,在班级“牛年拼牛画”的活动中,小刚同学用一个边长为8cm的正方形做成的七巧板(如图1)拼成了一头牛的图案(如图2),则牛头部所占的面积为( )
A.4 cm2 B.8 cm2 C.16 cm2 D.20 cm2
11.“汽车的雨刷把挡风玻璃上的雨水刷干净”,属于( )的实际应用.
A.点动成线 B.线动成面 C.面动成体 D.以上都不对
12.现有一个长方形,长和宽分别为和,绕它的一条边所在的直线旋转一周,得到的几何体的体积为( )
A. B. C.或 D.或
二、填空题
13.如图是用一副七巧板拼成的正方形,边长是10cm.图中小正方形(涂色部分)的面积是 .
14.线与线相交的地方形成点,点无 .
15.一个正方形去掉一个角后所得到的图形最少有 条边.
16.如图,将边长是的正方形绕它的对称轴(虚线处)旋转一周可以得到一个圆柱,则这个圆柱的表面积是 ,体积是 .(π取)
17.如图,已知的半径为,正方形的边长4,绕正方形无滑动的滚动一周(回到起点),则圆心的运动路线长是 .
三、解答题
18.将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现有一个长是、宽是的长方形,分别绕它的长、宽所在的直线旋转一周,得到不同的圆柱几何体,它们的体积分别是多大?
19.课本重现:如图,已知长方形的长为、宽为,将这个长方形分别绕它的长和宽所在直线旋转一周,得到两个圆柱甲、乙
(1)甲乙圆柱体形成的过程可以解释为________
A.点动成线 B.线动成面 C.面动成体
(2)当,时
①通过计算比较甲、乙圆柱体的侧面积的大小关系
②求甲圆柱体与乙圆柱体的体积比
(3)请直接写出甲、乙圆柱体的侧面积有什么关系,体积比有什么关系?(用字母和表示)
20.如图是一张长方形纸片,AB长为,BC长为.若将此长方形纸片绕它的一边所在直线旋转一周
(1)得到的几何体是 ,这个现象用数学知识解释为 ;
(2)若将这个长方形纸片绕它的一边所在直线旋转一周,求形成的几何体的体积.(结果保留)
21.如图,第二行的图形绕虚线旋转一周,便能形成第一行的某个几何体,用线连一连.
22.在多边形边上或内部取一点与多边形各顶点的连线,可将多边形分割成若干个小三角形,以四边形为例,图①给出了具体的分割方法,分别将四边形分割成了2个,3个,4个小三角形.
(1)请按照上述分割方法,将图②的五边形进行分割;
(2)如果按照上述的分割方法,n边形分别可以被分割成___________、___________、___________个小三角形.(用含n的代数式写出结论即可,不必画图)
23.下列几何体可以由平面图形绕其中一条直线旋转一周得到吗?
24.我们知道,将一个长方形绕它的一条边所在的直线旋转一周,得到的几何体是圆柱.现有一个长为,宽为的长方形,将这个长方形绕某条边所在直线旋转一周,求所得圆柱的体积是多少?(结果保留)
《5.2运动想象》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D A D C C B C B A C
题号 11 12
答案 B C
1.D
【分析】本题考查了认识平面图形,根据平面图形和立体图形的定义对各选项分析判断即可得解,熟练掌握平面图形和立体图形的定义是解此题的关键.
【详解】解:A、长方体是立体图形,故不符合题意;
B、圆锥体是立体图形,故不符合题意;
C、圆柱是立体图形,故不符合题意;
D、圆是平面图形,故符合题意;
故选:D.
2.A
【分析】这一现象为:点动成线.
【详解】解:笔尖在纸上快速滑动写出数字9,用数学知识解释为点动成线.
故选A.
【点睛】本题考查点,线,面,体之间的关系.熟练掌握点动成线,线动成面,面动成体,是解题的关键.
3.D
【分析】本题考查点、线、面、体,理解“点动成线”,“线动成面”,“面动成体”是正确解答的关键.根据“面动成体”进行判断即可.
【详解】解:将所给的图形绕虚线旋转一周得到的立体图形上、下是圆锥体,中间是圆柱体的组合体,因此选项D中的立体图形符合题意,
故选:D.
4.C
【分析】本题主要考查点、线、面、体,熟练掌握点、线、面、体直角的关系是解题的关键.直角三角形绕一条直角边旋转一周,得到的立体图形是圆锥.
【详解】解:直角三角形绕一条直角边旋转一周,可得到的立体图形是圆锥.
故选:C.
5.C
【分析】根据“面动成体”的知识解答即可.
【详解】在直角三角形中,,,以直角边为轴旋转后得到的是底面半径是6cm,高是8cm的圆锥.
故选:C
【点睛】本题主要考查了学生实际操作能力和空间想象能力,熟练掌握“面动成体”这一知识点是解题的关键.
6.B
【分析】本题考查生活中的数学现象,涉及几何基础尝试:点动成线、线动成面、面动成体,将生活中的现象与数学知识结合是解决问题的关键.
【详解】解:转动自行车的轮子,轮子上的辐条会形成一个圆面,用数学知识可以解释为线动成面,
故选:B.
7.C
【分析】分情况讨论分别去掉A、B、C三处的钉子时,组成长方形的长和宽各是多少,再根据长方形的面积公式进行解答即可.
【详解】解:当去掉A处的钉子时:这时长方形的长为4,则是其余三边长的长度和,是两条宽的长度和,则宽是,
则面积为:;
当去掉B处的钉子时:这时长方形的长为7,则是其余三边长的长度和,是两条宽的长度和,则宽是,
则面积为:;
当去掉C处的钉子时:这时长方形的长为5,则是其余三边长的长度和,是两条宽的长度和,则宽是,
则面积为:.
故选:C.
【点睛】本题考查了平面图形的认识与计算,利用分类讨论的思想是解题的关键.
8.B
【分析】本题主要考查七巧板中的面积计算,根据阴影部分面积正方形面积的一半,求解即可.
【详解】解:,
故选B.
9.A
【分析】根据面动成体逐项判断即得答案.
【详解】圆锥能由直角三角形绕轴旋转一周得到,
故选A.
【点睛】本题考查了点、线、面、体的相关知识,熟练掌握面动成体是解题关键.
10.C
【分析】由图1的正方形的边长为8cm,可求正方形的面积,再根据牛头所占面积为正方形面积的可得答案.
【详解】解:∵图1的正方形的边长为8cm,
∴正方形的面积是64cm2,
由牛的拼法可知,牛的头部占正方形的,
∴牛头部所占的面积是64×=16cm2,
故选:C.
【点睛】本题是一道趣味性探索题,结合我国传统玩具七巧板,用七巧板来拼接图形,可以培养学生动手能力,展开学生的丰富想象力.
11.B
【分析】本题考查点、线、面、体四者之间的关系,理解点动成线、线动成面、面动成体是解答的关键.根据线动成面求解即可.
【详解】解:“汽车的雨刷把挡风玻璃上的雨水刷干净”,属于线动成面的实际应用,
故选:B.
12.C
【分析】以不同的边为轴旋转一周,所得到的圆柱体的底面半径和高,根据圆柱体体积的计算方法进行计算即可.
【详解】解:绕着3cm的边为轴,旋转一周所得到的是底面半径为2cm,高为3cm的圆柱体,
因此体积为;
绕着2cm的边为轴,旋转一周所得到的是底面半径为3cm,高为2cm的圆柱体,
因此体积为,
故选:C.
【点睛】本题考查点、线、面、体,掌握圆柱体体积的计算方法是正确解答的前提,以不同的边为轴旋转得到的圆柱体的底面半径和高是正确计算的关键.
13.12.5
【分析】如图,将正方形分成4个大三角形,再将右面的三角形分成4个小三角形,阴影部分占2个小三角形,所以占右下大三角形的一半,它的面积就用正方形的面积除以4再除以2求得.
【详解】解:正方形的面积为10×10=100()
∴100÷4÷2=12.5()
∴涂色正方形的面积是12.5.
故答案为:12.5.
【点睛】本题考查了七巧板,利用了正方形的性质和等腰直角三角形的性质.解答本题的关键是把阴影部分的面积转化为正方形面积的几分之几.
14.大小
【解析】略
15.3
【分析】根据题意画出图形,注意各种情况,不要漏解.
【详解】如图所示:一个正方形去掉一个角后有3种情况,
∴最少有3条边.
故答案为:3.
【点睛】此题主要考查了多边形,关键是考虑全面,分类讨论.
16. 50.24
【分析】本题考查圆柱的体积,表面积,关键是掌握圆柱体积,侧面积的计算公式.由圆柱体积,侧面积的计算公式,即可求解.
【详解】解∶由题意知∶圆柱的底面圆半径,圆柱的高,
圆柱的体积
;
圆柱的底面圆的面积,圆柱的侧面积,
∴圆柱的表面积.
故答案为∶,.
17./
【分析】根据绕正方形无滑动的滚动一周,圆心O通过的距离正好为正方形的周长和半径为1的一个圆的周长之和,进行解答即可.
【详解】解:圆心的运动轨迹如图所示:
绕正方形无滑动的滚动一周,则圆心的运动路线长为:
.
故答案为:.
【点睛】本题主要考查了圆的周长正方形的周长,解题的关键是熟练掌握圆心的运动路线轨迹.
18.和
【分析】本题考查圆柱体的体积的求法,解答本题需要同学们熟练掌握圆柱体的体积公式,分类讨论是解题的关键.
根据圆柱体的体积=底面积×高求解,注意底面半径和高互换得圆柱体的两种情况.
【详解】解:①绕长所在的直线旋转一周得到圆柱体积为:;
②绕宽所在的直线旋转一周得到圆柱体积为:;
答:它们的体积分别是和.
19.(1)C
(2)①侧面积相等 ②体积比为
(3)侧面积相等;体积比为
【分析】此题考查了点、线、面、体之间的关系以及圆柱的侧面积和体积公式,掌握以上知识点是解答本题的关键.
(1)根据平面旋转后得到圆柱体即可知道是面动成体;
(2)① 分别计算出甲、乙圆柱体的侧面积,然后比较大小即可;
②分别计算出甲、乙圆柱体的体积,求出其比值即可;
(3)根据(2)计算的结果得出甲、乙圆柱体侧面积的关系以及体积比的关系.
【详解】(1)解:根据题意得:甲乙圆柱体形成的过程可以解释为面动成体,
故选:C;
(2)解:①甲圆柱的侧面积为:,
乙圆柱的侧面积为:,
所以甲乙两圆柱的侧面积相等;
②甲圆柱的体积为:,
乙圆柱的体积为:,
所以甲乙两圆柱的体积比为:;
(3)解:由(2)知甲、乙圆柱体的侧面积相等,体积比.
20.(1)圆柱,面动成体
(2)形成的几何体的体积是cm或cm.
【分析】(1)旋转后的几何体是圆柱,用数学知识解释为面动成体;
(2)分两种情况,根据圆柱的体积公式计算即可求解.
【详解】(1)解:若将此长方形纸片绕它的一边所在直线旋转一周,则形成的几何体是圆柱,这个现象用数学知识解释为面动成体;
故答案为:圆柱,面动成体
(2)情况①,绕AB边所在直线旋转:
(cm);
情况②,绕BC边所在直线旋转:
(cm);
故形成的几何体的体积是cm或cm.
【点睛】本题主要考查的是点、线、面、体,根据图形确定出圆柱的底面半径和高的长是解题的关键.
21.见解析
【分析】根据旋转的特点和各几何图形的特性判断即可.
【详解】解:如图所示:
【点睛】本题考查了点、线、面、体,解决本题的关键是掌握点动成线,线动成面,面动成体.
22.(1)见解析
(2);;n
【分析】本题考查了多边形的对角线,得出规律是解此题的关键.
(1)根据题意结合图形分割即可得解;
(2)根据(1)的解答,从特殊到一般总结即可得解.
【详解】(1)解:将图②的五边形进行分割如图所示:
;
(2)解:结合题干所给图形可得:
如果按照上述的分割方法,n边形分别可以被分割成、、n个小三角形.
23.(1)能;(2)不能;(3)能;(4)能
【分析】由“面动成体”逐项进行判断即可.
【详解】解:由“面动成体”可得,
(1)的几何体能由平面图形绕其中一条直线旋转一周得到,
(2)的几何体不能由平面图形绕其中一条直线旋转一周得到,
(3)的几何体能由平面图形绕其中一条直线旋转一周得到,
(4)的几何体能由平面图形绕其中一条直线旋转一周得到,
【点睛】本题考查点、线、面、体,理解“点动成线”“线动成面”“面动成体”是正确判断的前提.
24.得到的圆柱体积是或.
【分析】本题考查了面旋转成体,圆柱的体积公式,分当为圆柱的半径和为圆柱的半径两种情况讨论,结合体积公式计算即可,熟练掌握圆柱的体积公式是解题的关键.
【详解】解:当为圆柱的半径时,
旋转一周得到的圆柱体积为:;
当为圆柱的半径时,
旋转一周得到的圆柱体积为:,
答:得到的圆柱体积是或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.2运动想象
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列图形中,属于平面图形的是( )
A.长方体 B.圆锥体 C.圆柱 D.圆
2.“笔尖在纸上快速滑动写出数字9”运用数学知识解释这一现象为( )
A.点动成线 B.线动成面
C.面动成体 D.面与面相交得线
3.如图,绕虚线旋转一周可以得到的立体图形是( )
A. B. C. D.
4.将如图所示的平面图形绕直线旋转一周,可得到的立体图形是( )
A. B.
C. D.
5.如图,在直角三角形中,,,以直角边为轴旋转后得到的是( )
A.底面半径是8cm,高是6cm的圆锥 B.底面直径是8cm,高是6cm的圆锥
C.底面半径是6cm,高是8cm的圆锥 D.底面直径是6cm,高是8cm的圆锥
6.转动自行车的轮子,轮子上的辐条会形成一个圆面,用数学知识可以解释为( )
A.点动成线 B.线动成面 C.面动成体 D.面与面相交成线
7.一根彩绳和A、B、C三个钉子围成如图的三角形,如果将三角形的一个角顶点处的钉子去掉,并将这条彩绳钉成一个长方形, 则所钉成的长方形的面积是( )
A.7或15 B.16或15 C.7或15或16 D.无数个答案
8.如图,用对角线长为4的正方形,做了一套七巧板,拼成如图所示的一座桥,则桥中阴影部分的面积为( )
A.2 B.4 C.6 D.8
9.下图中的几何体(圆锥)是由下列( )平面图形绕轴旋转一周得到的.
A. B. C. D.
10.今年是牛年,在班级“牛年拼牛画”的活动中,小刚同学用一个边长为8cm的正方形做成的七巧板(如图1)拼成了一头牛的图案(如图2),则牛头部所占的面积为( )
A.4 cm2 B.8 cm2 C.16 cm2 D.20 cm2
11.“汽车的雨刷把挡风玻璃上的雨水刷干净”,属于( )的实际应用.
A.点动成线 B.线动成面 C.面动成体 D.以上都不对
12.现有一个长方形,长和宽分别为和,绕它的一条边所在的直线旋转一周,得到的几何体的体积为( )
A. B. C.或 D.或
二、填空题
13.如图是用一副七巧板拼成的正方形,边长是10cm.图中小正方形(涂色部分)的面积是 .
14.线与线相交的地方形成点,点无 .
15.一个正方形去掉一个角后所得到的图形最少有 条边.
16.如图,将边长是的正方形绕它的对称轴(虚线处)旋转一周可以得到一个圆柱,则这个圆柱的表面积是 ,体积是 .(π取)
17.如图,已知的半径为,正方形的边长4,绕正方形无滑动的滚动一周(回到起点),则圆心的运动路线长是 .
三、解答题
18.将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现有一个长是、宽是的长方形,分别绕它的长、宽所在的直线旋转一周,得到不同的圆柱几何体,它们的体积分别是多大?
19.课本重现:如图,已知长方形的长为、宽为,将这个长方形分别绕它的长和宽所在直线旋转一周,得到两个圆柱甲、乙
(1)甲乙圆柱体形成的过程可以解释为________
A.点动成线 B.线动成面 C.面动成体
(2)当,时
①通过计算比较甲、乙圆柱体的侧面积的大小关系
②求甲圆柱体与乙圆柱体的体积比
(3)请直接写出甲、乙圆柱体的侧面积有什么关系,体积比有什么关系?(用字母和表示)
20.如图是一张长方形纸片,AB长为,BC长为.若将此长方形纸片绕它的一边所在直线旋转一周
(1)得到的几何体是 ,这个现象用数学知识解释为 ;
(2)若将这个长方形纸片绕它的一边所在直线旋转一周,求形成的几何体的体积.(结果保留)
21.如图,第二行的图形绕虚线旋转一周,便能形成第一行的某个几何体,用线连一连.
22.在多边形边上或内部取一点与多边形各顶点的连线,可将多边形分割成若干个小三角形,以四边形为例,图①给出了具体的分割方法,分别将四边形分割成了2个,3个,4个小三角形.
(1)请按照上述分割方法,将图②的五边形进行分割;
(2)如果按照上述的分割方法,n边形分别可以被分割成___________、___________、___________个小三角形.(用含n的代数式写出结论即可,不必画图)
23.下列几何体可以由平面图形绕其中一条直线旋转一周得到吗?
24.我们知道,将一个长方形绕它的一条边所在的直线旋转一周,得到的几何体是圆柱.现有一个长为,宽为的长方形,将这个长方形绕某条边所在直线旋转一周,求所得圆柱的体积是多少?(结果保留)
《5.2运动想象》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D A D C C B C B A C
题号 11 12
答案 B C
1.D
【分析】本题考查了认识平面图形,根据平面图形和立体图形的定义对各选项分析判断即可得解,熟练掌握平面图形和立体图形的定义是解此题的关键.
【详解】解:A、长方体是立体图形,故不符合题意;
B、圆锥体是立体图形,故不符合题意;
C、圆柱是立体图形,故不符合题意;
D、圆是平面图形,故符合题意;
故选:D.
2.A
【分析】这一现象为:点动成线.
【详解】解:笔尖在纸上快速滑动写出数字9,用数学知识解释为点动成线.
故选A.
【点睛】本题考查点,线,面,体之间的关系.熟练掌握点动成线,线动成面,面动成体,是解题的关键.
3.D
【分析】本题考查点、线、面、体,理解“点动成线”,“线动成面”,“面动成体”是正确解答的关键.根据“面动成体”进行判断即可.
【详解】解:将所给的图形绕虚线旋转一周得到的立体图形上、下是圆锥体,中间是圆柱体的组合体,因此选项D中的立体图形符合题意,
故选:D.
4.C
【分析】本题主要考查点、线、面、体,熟练掌握点、线、面、体直角的关系是解题的关键.直角三角形绕一条直角边旋转一周,得到的立体图形是圆锥.
【详解】解:直角三角形绕一条直角边旋转一周,可得到的立体图形是圆锥.
故选:C.
5.C
【分析】根据“面动成体”的知识解答即可.
【详解】在直角三角形中,,,以直角边为轴旋转后得到的是底面半径是6cm,高是8cm的圆锥.
故选:C
【点睛】本题主要考查了学生实际操作能力和空间想象能力,熟练掌握“面动成体”这一知识点是解题的关键.
6.B
【分析】本题考查生活中的数学现象,涉及几何基础尝试:点动成线、线动成面、面动成体,将生活中的现象与数学知识结合是解决问题的关键.
【详解】解:转动自行车的轮子,轮子上的辐条会形成一个圆面,用数学知识可以解释为线动成面,
故选:B.
7.C
【分析】分情况讨论分别去掉A、B、C三处的钉子时,组成长方形的长和宽各是多少,再根据长方形的面积公式进行解答即可.
【详解】解:当去掉A处的钉子时:这时长方形的长为4,则是其余三边长的长度和,是两条宽的长度和,则宽是,
则面积为:;
当去掉B处的钉子时:这时长方形的长为7,则是其余三边长的长度和,是两条宽的长度和,则宽是,
则面积为:;
当去掉C处的钉子时:这时长方形的长为5,则是其余三边长的长度和,是两条宽的长度和,则宽是,
则面积为:.
故选:C.
【点睛】本题考查了平面图形的认识与计算,利用分类讨论的思想是解题的关键.
8.B
【分析】本题主要考查七巧板中的面积计算,根据阴影部分面积正方形面积的一半,求解即可.
【详解】解:,
故选B.
9.A
【分析】根据面动成体逐项判断即得答案.
【详解】圆锥能由直角三角形绕轴旋转一周得到,
故选A.
【点睛】本题考查了点、线、面、体的相关知识,熟练掌握面动成体是解题关键.
10.C
【分析】由图1的正方形的边长为8cm,可求正方形的面积,再根据牛头所占面积为正方形面积的可得答案.
【详解】解:∵图1的正方形的边长为8cm,
∴正方形的面积是64cm2,
由牛的拼法可知,牛的头部占正方形的,
∴牛头部所占的面积是64×=16cm2,
故选:C.
【点睛】本题是一道趣味性探索题,结合我国传统玩具七巧板,用七巧板来拼接图形,可以培养学生动手能力,展开学生的丰富想象力.
11.B
【分析】本题考查点、线、面、体四者之间的关系,理解点动成线、线动成面、面动成体是解答的关键.根据线动成面求解即可.
【详解】解:“汽车的雨刷把挡风玻璃上的雨水刷干净”,属于线动成面的实际应用,
故选:B.
12.C
【分析】以不同的边为轴旋转一周,所得到的圆柱体的底面半径和高,根据圆柱体体积的计算方法进行计算即可.
【详解】解:绕着3cm的边为轴,旋转一周所得到的是底面半径为2cm,高为3cm的圆柱体,
因此体积为;
绕着2cm的边为轴,旋转一周所得到的是底面半径为3cm,高为2cm的圆柱体,
因此体积为,
故选:C.
【点睛】本题考查点、线、面、体,掌握圆柱体体积的计算方法是正确解答的前提,以不同的边为轴旋转得到的圆柱体的底面半径和高是正确计算的关键.
13.12.5
【分析】如图,将正方形分成4个大三角形,再将右面的三角形分成4个小三角形,阴影部分占2个小三角形,所以占右下大三角形的一半,它的面积就用正方形的面积除以4再除以2求得.
【详解】解:正方形的面积为10×10=100()
∴100÷4÷2=12.5()
∴涂色正方形的面积是12.5.
故答案为:12.5.
【点睛】本题考查了七巧板,利用了正方形的性质和等腰直角三角形的性质.解答本题的关键是把阴影部分的面积转化为正方形面积的几分之几.
14.大小
【解析】略
15.3
【分析】根据题意画出图形,注意各种情况,不要漏解.
【详解】如图所示:一个正方形去掉一个角后有3种情况,
∴最少有3条边.
故答案为:3.
【点睛】此题主要考查了多边形,关键是考虑全面,分类讨论.
16. 50.24
【分析】本题考查圆柱的体积,表面积,关键是掌握圆柱体积,侧面积的计算公式.由圆柱体积,侧面积的计算公式,即可求解.
【详解】解∶由题意知∶圆柱的底面圆半径,圆柱的高,
圆柱的体积
;
圆柱的底面圆的面积,圆柱的侧面积,
∴圆柱的表面积.
故答案为∶,.
17./
【分析】根据绕正方形无滑动的滚动一周,圆心O通过的距离正好为正方形的周长和半径为1的一个圆的周长之和,进行解答即可.
【详解】解:圆心的运动轨迹如图所示:
绕正方形无滑动的滚动一周,则圆心的运动路线长为:
.
故答案为:.
【点睛】本题主要考查了圆的周长正方形的周长,解题的关键是熟练掌握圆心的运动路线轨迹.
18.和
【分析】本题考查圆柱体的体积的求法,解答本题需要同学们熟练掌握圆柱体的体积公式,分类讨论是解题的关键.
根据圆柱体的体积=底面积×高求解,注意底面半径和高互换得圆柱体的两种情况.
【详解】解:①绕长所在的直线旋转一周得到圆柱体积为:;
②绕宽所在的直线旋转一周得到圆柱体积为:;
答:它们的体积分别是和.
19.(1)C
(2)①侧面积相等 ②体积比为
(3)侧面积相等;体积比为
【分析】此题考查了点、线、面、体之间的关系以及圆柱的侧面积和体积公式,掌握以上知识点是解答本题的关键.
(1)根据平面旋转后得到圆柱体即可知道是面动成体;
(2)① 分别计算出甲、乙圆柱体的侧面积,然后比较大小即可;
②分别计算出甲、乙圆柱体的体积,求出其比值即可;
(3)根据(2)计算的结果得出甲、乙圆柱体侧面积的关系以及体积比的关系.
【详解】(1)解:根据题意得:甲乙圆柱体形成的过程可以解释为面动成体,
故选:C;
(2)解:①甲圆柱的侧面积为:,
乙圆柱的侧面积为:,
所以甲乙两圆柱的侧面积相等;
②甲圆柱的体积为:,
乙圆柱的体积为:,
所以甲乙两圆柱的体积比为:;
(3)解:由(2)知甲、乙圆柱体的侧面积相等,体积比.
20.(1)圆柱,面动成体
(2)形成的几何体的体积是cm或cm.
【分析】(1)旋转后的几何体是圆柱,用数学知识解释为面动成体;
(2)分两种情况,根据圆柱的体积公式计算即可求解.
【详解】(1)解:若将此长方形纸片绕它的一边所在直线旋转一周,则形成的几何体是圆柱,这个现象用数学知识解释为面动成体;
故答案为:圆柱,面动成体
(2)情况①,绕AB边所在直线旋转:
(cm);
情况②,绕BC边所在直线旋转:
(cm);
故形成的几何体的体积是cm或cm.
【点睛】本题主要考查的是点、线、面、体,根据图形确定出圆柱的底面半径和高的长是解题的关键.
21.见解析
【分析】根据旋转的特点和各几何图形的特性判断即可.
【详解】解:如图所示:
【点睛】本题考查了点、线、面、体,解决本题的关键是掌握点动成线,线动成面,面动成体.
22.(1)见解析
(2);;n
【分析】本题考查了多边形的对角线,得出规律是解此题的关键.
(1)根据题意结合图形分割即可得解;
(2)根据(1)的解答,从特殊到一般总结即可得解.
【详解】(1)解:将图②的五边形进行分割如图所示:
;
(2)解:结合题干所给图形可得:
如果按照上述的分割方法,n边形分别可以被分割成、、n个小三角形.
23.(1)能;(2)不能;(3)能;(4)能
【分析】由“面动成体”逐项进行判断即可.
【详解】解:由“面动成体”可得,
(1)的几何体能由平面图形绕其中一条直线旋转一周得到,
(2)的几何体不能由平面图形绕其中一条直线旋转一周得到,
(3)的几何体能由平面图形绕其中一条直线旋转一周得到,
(4)的几何体能由平面图形绕其中一条直线旋转一周得到,
【点睛】本题考查点、线、面、体,理解“点动成线”“线动成面”“面动成体”是正确判断的前提.
24.得到的圆柱体积是或.
【分析】本题考查了面旋转成体,圆柱的体积公式,分当为圆柱的半径和为圆柱的半径两种情况讨论,结合体积公式计算即可,熟练掌握圆柱的体积公式是解题的关键.
【详解】解:当为圆柱的半径时,
旋转一周得到的圆柱体积为:;
当为圆柱的半径时,
旋转一周得到的圆柱体积为:,
答:得到的圆柱体积是或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
