5.3转化表达暑假预习练(含解析) 苏科版数学七年级上册
文档属性
| 名称 | 5.3转化表达暑假预习练(含解析) 苏科版数学七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 575.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-04 19:14:07 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
5.3转化表达
学校:___________姓名:___________班级:___________考号:___________
一、单选题
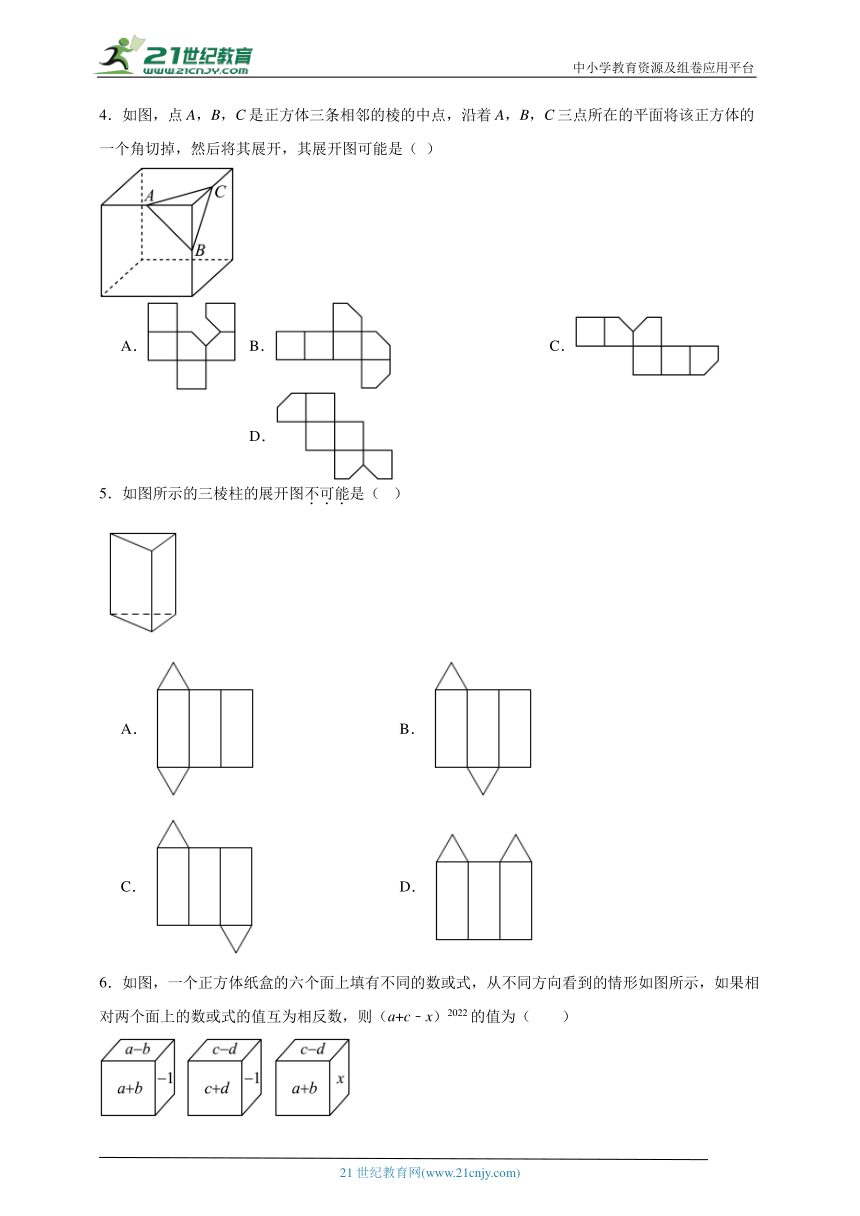
1.如图所示的几何体是由一些小正方体组成的,那么从左边看它的图形是( )
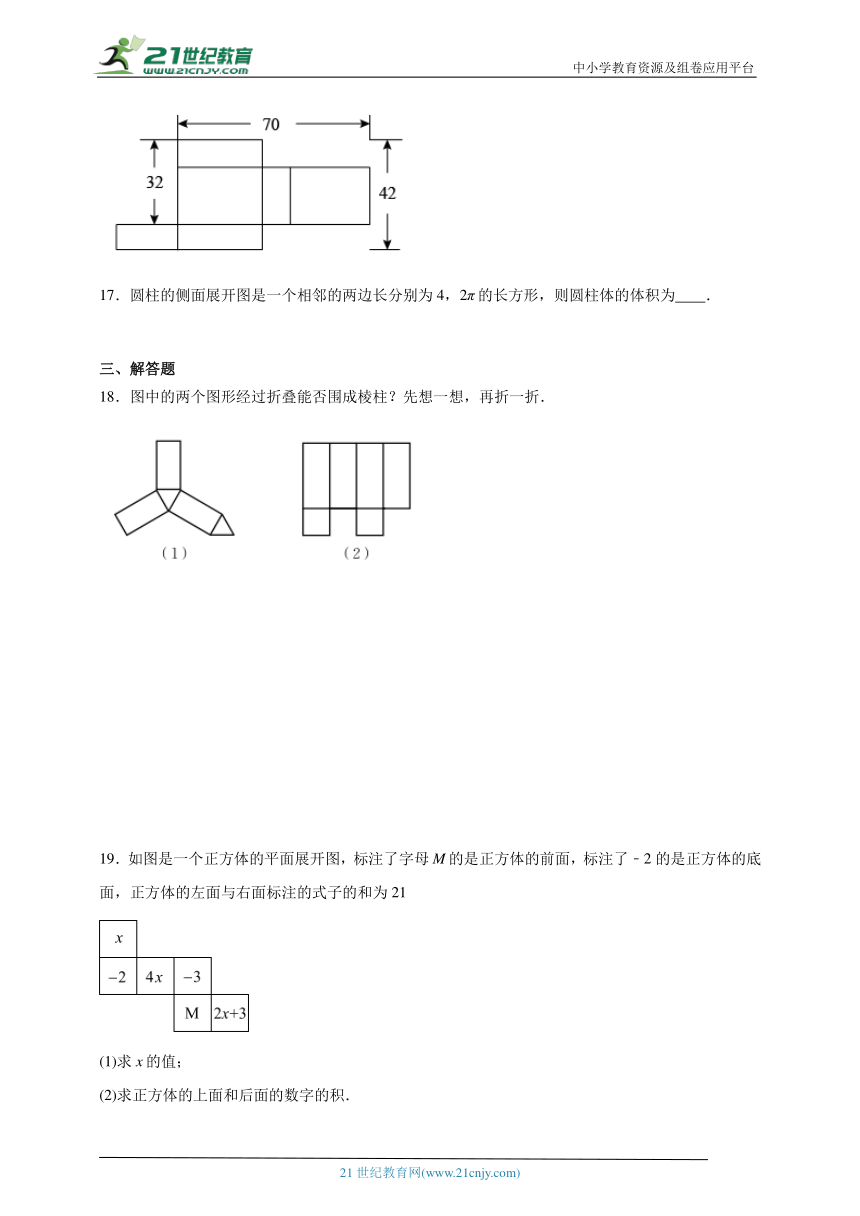
A. B. C. D.
2.下列图形中,可以折叠成三棱柱的是( )
A. B. C. D.
3.在如图所示的图形中是正方体的展开图的有( )
A.3种 B.4种 C.5种 D.6种
4.如图,点A,B,C是正方体三条相邻的棱的中点,沿着A,B,C三点所在的平面将该正方体的一个角切掉,然后将其展开,其展开图可能是( )
A. B. C. D.
5.如图所示的三棱柱的展开图不可能是( )
A. B.
C. D.
6.如图,一个正方体纸盒的六个面上填有不同的数或式,从不同方向看到的情形如图所示,如果相对两个面上的数或式的值互为相反数,则(a+c﹣x)2022的值为( )
A.1 B.﹣1 C.0 D.2022
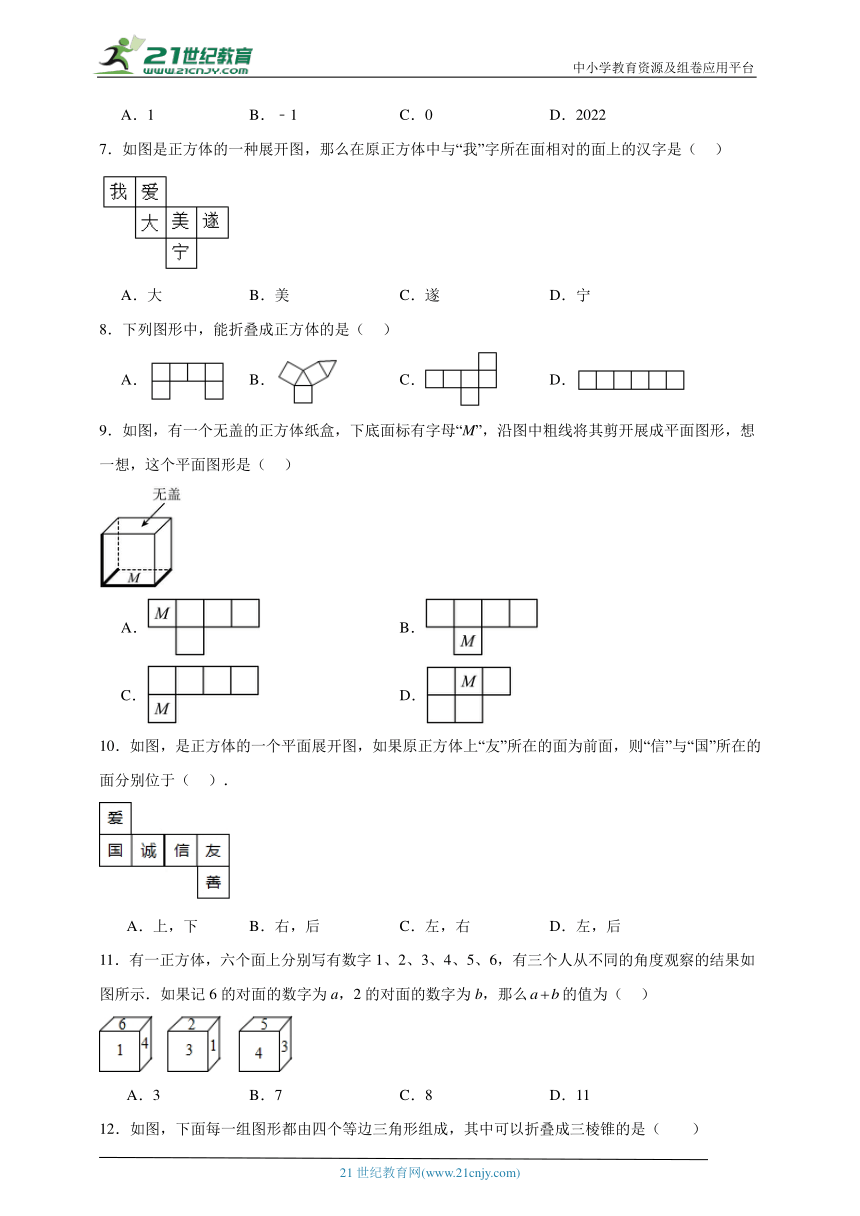
7.如图是正方体的一种展开图,那么在原正方体中与“我”字所在面相对的面上的汉字是( )
A.大 B.美 C.遂 D.宁
8.下列图形中,能折叠成正方体的是( )
A. B. C. D.
9.如图,有一个无盖的正方体纸盒,下底面标有字母“M”,沿图中粗线将其剪开展成平面图形,想一想,这个平面图形是( )
A. B.
C. D.
10.如图,是正方体的一个平面展开图,如果原正方体上“友”所在的面为前面,则“信”与“国”所在的面分别位于( ).
A.上,下 B.右,后 C.左,右 D.左,后
11.有一正方体,六个面上分别写有数字1、2、3、4、5、6,有三个人从不同的角度观察的结果如图所示.如果记6的对面的数字为a,2的对面的数字为b,那么的值为( )
A.3 B.7 C.8 D.11
12.如图,下面每一组图形都由四个等边三角形组成,其中可以折叠成三棱锥的是( )
A.仅图① B.图①和图② C.图②和图③ D.图①和图③
二、填空题
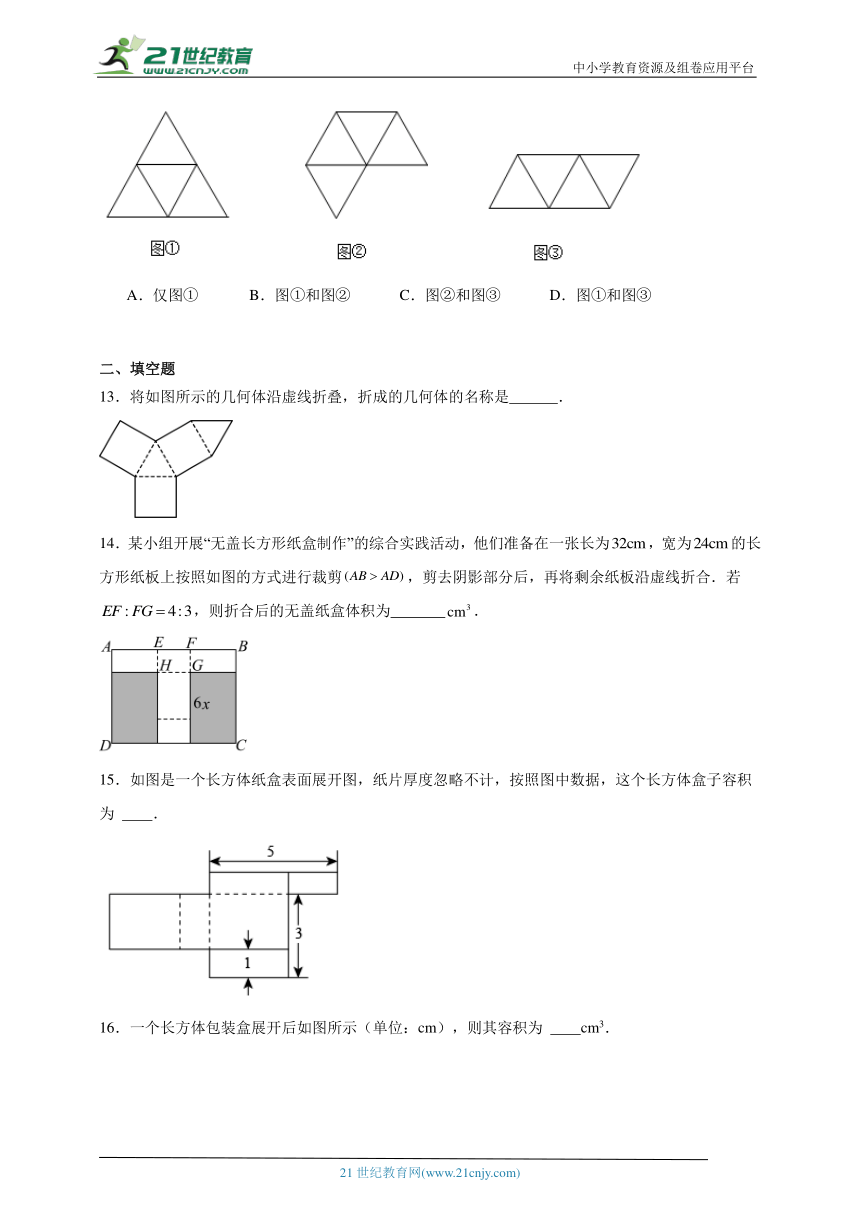
13.将如图所示的几何体沿虚线折叠,折成的几何体的名称是 .
14.某小组开展“无盖长方形纸盒制作”的综合实践活动,他们准备在一张长为,宽为的长方形纸板上按照如图的方式进行裁剪,剪去阴影部分后,再将剩余纸板沿虚线折合.若,则折合后的无盖纸盒体积为 .
15.如图是一个长方体纸盒表面展开图,纸片厚度忽略不计,按照图中数据,这个长方体盒子容积为 .
16.一个长方体包装盒展开后如图所示(单位:cm),则其容积为 cm3.
17.圆柱的侧面展开图是一个相邻的两边长分别为4,2π的长方形,则圆柱体的体积为 .
三、解答题
18.图中的两个图形经过折叠能否围成棱柱?先想一想,再折一折.
19.如图是一个正方体的平面展开图,标注了字母M的是正方体的前面,标注了﹣2的是正方体的底面,正方体的左面与右面标注的式子的和为21
(1)求x的值;
(2)求正方体的上面和后面的数字的积.
20.下面是一个多面体的表面展开图每个面上都标注了字母,(所有字母都写在这一多面体的外表面)请根据要求回答问题:
(1)如果面在前面,从左边看是,那么哪一面会在上面?
(2)如果从右面看是面面,面在后边那么哪一面会在上面?
(3)如果面在多面体的底部,从右边看是,那么哪一面会在前面.
21.小丽同学周末帮妈妈拆完快递后,将包装盒展开,进行了测量,结果如图所示.已知长方体盒子的长比宽多3cm.
(1)求长方体盒子的长和宽.
(2)求这个包装盒的体积.
22.如图是一个正方体的表面展开图,若正方体中相对的面上的数互为相反数,则、x、y的值分别为多少?
23.如图,在正方体能看到的面上写着1,2,3,而在展开图上已写了2个或1个指定的数,试在展开图的其他各面上写上适当的数,使其相对面上的两数之和为7.
24.有一种牛奶软包装盒如图1所示.为了生产这种包装盒,需要先画出展开图纸样.
(1)如图2给出三种纸样甲、乙、丙,在甲、乙、丙中,正确的有______________.
(2)利用你所选的一种纸样,求出包装盒的侧面积和表面积(侧面积与两个底面积的和)
《5.3转化表达》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B C D D A B C B C
题号 11 12
答案 B D
1.B
【分析】本题考查从不同角度看几何体,得出从左面看几何体得到的图形即可解题.
【详解】解:从左边看它的图形是
,
故选B.
2.B
【分析】本题考查几何体展开图的判断,根据展开图的特点即可判断.
【详解】解:A、根据图形判断是圆锥展开图,不符合题意;
B、根据图形判断是三棱柱展开图,符合题意;
C、根据图形判断是正方体展开图,不符合题意;
D、根据图形判断是四棱锥展开图,不符合题意.
故选:B.
3.C
【分析】根据正方体展开图的11种形式对各小题分析判断即可得解.
【详解】解:由正方体的11种展开图的特征可知,图1、图2、图3、图4、图6都是正方体的展开图,图5出现了“田”字,不能围成正方体.
∴以上是正方体的展开图的有5种.
故选:C.
【点睛】本题考查了正方体的展开图,熟记展开图的11种形式是解题的关键,利用不是正方体展开图的“一线不过四、田凹应弃之”(即不能出现同一行有多于4个正方形的情况,不能出现田字形、凹字形的情况)判断也可.
4.D
【分析】考查了截一个几何体和几何体的展开图.由平面图形的折叠及立体图形的表面展开图的特点解题.
【详解】解:A、折叠后两个剪去三角形与另一个剪去的三角形不交于一个顶点,不符合题意;
B、折叠后两个剪去三角形与另一个剪去的三角形不交于一个顶点,不符合题意;
C、折叠后两个剪去三角形与另一个剪去的三角形不交于一个顶点,不符合题意;
D、折叠后两个剪去三角形与另一个剪去的三角形交于一个顶点,与正方体三个剪去三角形交于一个顶点符合,符合题意.
故选:D.
5.D
【分析】三棱柱的表面展开图的特点,由三个长方形的侧面和上下两个三角形的底面组成.从而可得答案.
【详解】解:选项A、B、C均可能是该三棱柱展开图,不符合题意,
而选项D中的两个底面会重叠,不可能是它的表面展开图,符合题意,
故选:D.
【点睛】考查了几何体的展开图,动手折叠一下,有助于空间想象力的培养.
6.A
【分析】结合图形找出相对面,求出a+c与x的值,代入式子中即可解答.
【详解】解:由图可知:
a+b与c+d为相对面,a b与c d为相对面,x与 1为相对面,
∵相对两个面上的数或式的值互为相反数,
∴a+b= (c+d)①,
a b= (c d)②,
x=1,
∴①+②得:2a= c d c+d,
2a= 2c,
2a+2c=0,
∴a+c=0,
∴(a+c x)2022=(0 1)2022=1,
故选:A.
【点睛】本题考查了正方体相对两个面上的文字,结合图形找出相对面求出a+c与x的值是解题的关键.
7.B
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【详解】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“我”与“美”是相对面.
故选:B.
【点睛】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手.
8.C
【分析】根据正方体展开图的常见形式作答即可.注意只要有“田”“凹”字格的展开图都不是正方体的表面展开图.
【详解】解:A、不能折叠成一个正方体,故选项不符合题意;
B、能折叠成三棱柱,故选项不符合题意;
C、能折叠成一个正方体,故选项正确,符合题意;
D、不能折叠成正方体,故选项不符合题意.
故选:C.
【点睛】本题考查了展开图折叠成几何体.能组成正方体的“一,四,一”“三,三”“二,二,二”“一,三,二”的基本形态要记牢.
9.B
【分析】由平面图形的折叠及正方体的展开图解题.正方体共有11种表面展开图,把11种展开图都去掉一个面得无盖的正方体展开图,把相同的归为一种得无盖正方体有8种表面展开图.
【详解】解:选项A经过折叠后,标有字母“M”的面不是下底面,
选项C折叠后,不是沿图中粗线将其剪开的,
选项D不可能折叠为正方体,
B正确.
故选:B.
10.C
【分析】正方体的平面展开图中,相对的两个面中间必须隔着一个小正方形,根据这一特点,结合题意可正确解答.
【详解】解:如果原正方体上“友”所在的面为前面,则“信”所在的面为左面,
所以相对的正方体的右面是“国”.
故选C.
【点睛】本题考查正方体相对两个面上的文字,解决本题的关键是要熟练掌握正方体展开图形相对两个面上的文字确定的方法.
11.B
【分析】由图一和图二可看出1的对面的数字是5;再由图二和图三可看出3的对面的数字是6,从而2的对面的数字是4.
【详解】解:从3个小立方体上的数可知,
与写有数字1的面相邻的面上数字是2,3,4,6,
所以数字1面对数字5,
同理,立方体面上数字3对6.
故立方体面上数字2对4.
则a=3,b=4,
那么a+b=3+4=7.
故选B.
【点睛】本题考查灵活运用正方体的相对面解答问题,立意新颖,是一道不错的题.解题的关键是按照相邻和所给图形得到相对面的数字.
12.D
【分析】由平面图形的折叠及三棱锥的展开图解题.
【详解】解:只有图①、图③能够折叠围成一个三棱锥.
故选:D.
【点睛】本题考查了展开图折叠成几何体的知识,属于基础题型.
13.三棱柱
【分析】本题考查作图-应用与设计作图.由平面图形的折叠的特点解题.
【详解】解:三个长方形和两个三角形能围成三棱柱,
故,将它折叠能得到三棱柱;
故答案为:三棱柱.
14.
【分析】本题考查了矩形的性质和折叠的性质.设,,则,解得,再根据长方体的体积公式计算即可求解.
【详解】解:如图,
∵,
∴设,,
∴,
∴,
∵,
∴,
解得,
∴,,,
∴折合后的无盖纸盒体积为,
故答案为:.
15.6
【分析】根据题意确定出长方体纸盒的长、宽、高,求出容积即可.
【详解】
底面的宽是,
底面的长是,
长方体的高是1,
长方体盒子容积为:.
故答案为:6.
【点睛】
此题考查了几何体的展开图,找出长方体的长、宽、高是解本题的关键.
16.6600
【分析】根据题意分别求出长方体的长、宽、高,再根据长方体的体积公式计算即可求解.
【详解】解:由题意可得,该长方体的高为:42﹣32=10(cm),宽为:32﹣10=22(cm),长为:(70﹣10)÷2=30(cm),
故其容积为:30×10×22=6600(cm3),
故答案为:6600.
【点睛】本题考查了几何体的展开图,解题的关键是得到长方体的长宽高.
17.4π或8/8或4π
【分析】
分两种情况:①以2π为底面周长,4为高;②以4为圆柱体的底面周长,2π为高;分别求解即可.
【详解】
解:①以2π为底面周长,4为高,
此时圆柱体的底面半径为=1,
∴圆柱体的体积为π×12×4=4π,
②以4为圆柱体的底面周长,2π为高,
此时圆柱体的底面半径为,
∴圆柱体的体积为π×()2×2π=8,
故答案为:4π或8.
【点睛】
本题考查圆柱体的展开与折叠,理解圆柱体表面展开图与圆柱体之间的关系是解决问题的关键.
18.(1)能围成三棱柱;(2)不能围成棱柱.
【分析】分别利用已知平面展开图进而分析得出答案.
【详解】解:如图(1)可以折成三棱柱,
如图(2)不能折成棱柱.
【点睛】本题主要考查展开图折叠成几何体的知识点,熟记常见立体图形的平面展开图是解决此类问题的关键.
19.(1)x=3
(2)-9
【分析】(1)正方体的表面展开图,相对的面之间一定相隔一个正方形确定出相对面,然后列出方程求解即可;
(2)确定出上面和底面上的两个数字-2和-3,然后相加即可.
【详解】(1)解:由正方体表面展开图的“相间、Z端是对面”可知,
“x”与“M”是相对的面,
“﹣2”与“﹣3”是相对的面,
“4x”与“2x+3”是相对的面,
又因为标注了字母M的是正方体的前面,标注了﹣2的是正方体的底面,
所以标注了字母x的是正方体的后面,标注了﹣3的是正方体的上面,
因此标注“4x”与“2x+3”是左面和右面,
又因为正方体的左面与右面标注的式子的和为21,
所以4x+2x+3=21,
解得x=3;
(2)解:因为标注了字母x的是正方体的后面,标注了﹣3的是正方体的上面,而x=3,
所以正方体的上面和后面的数字的积为﹣3×3=﹣9.
【点睛】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题是解题的关键.
20.(1)面会在上面;(2)面会在上面;(3)面会在前面
【分析】利用长方体及其表面展开图的特点解题.这是一个长方体的平面展开图,共有六个面,其中面“A”与面“F”相对,面“B”与面“D”相对,面“C”与面“E”相对.
【详解】解:(1)由图可知,如果F面在前面,B面在左面,那么“E”面下面,∵面“C”与面“E”相对,∴C面会在上面;
(2)由图可知,如果C面在右面,D面在后面,那么“F”面在下面,∵面“A”与面“F”相对,∴A面在上面.
(3)由图可知,如果面在多面体的底部,从右边看是,那么“E”面在后面,∵面“C”与面“E”相对,∴ 面会在前面
【点睛】考查了几何体的展开图,注意正方体的空间图形,从相对面入手,分析及解答问题.
21.(1)长方体盒子的长为,宽为;
(2)这个包装盒的体积是.
【分析】本题考查了长方体的展开图,关键是得到长方体的长,宽,高.
(1)要求长方体的体积,需知长方体的长,宽,高,结合图形可知2个宽2个高20,依此可求长方体盒子的宽;再根据长方体盒子的长宽3,可求长方体盒子的长;
(2)根据长方体的体积公式即可求解.
【详解】(1)解:长方体盒子的宽为,
长方体盒子的长为,
答:长方体盒子的长为,宽为;
(2)解:这个包装盒的体积为.
答:这个包装盒的体积是.
22.,,
【分析】本题主要考查的是正方体相对面上的文字,相反数的定义.根据正方体的展开图中可得“y”与“x”是对面,“5”与“”是对面,从而可根据相反数的定义求得x的值及y的值.
【详解】解:∵“y”与“x”是对面,“5”与“”是对面,正方体中相对的面上的数互为相反数,
∴,,
解得.
23.见解析
【分析】先确定数1、2、3所在面的相对面上的数,再根据正方体的展开图特点即可得.
【详解】由题意得:数1所在面的相对面上的数为,
数2所在面的相对面上的数为,
数3所在面的相对面上的数为,
则填图如下:
【点睛】本题考查了正方体的展开图,熟练掌握正方体的展开图特点是解题关键.
24.(1)甲、丙;(2)侧面积=2ah+2bh;包装盒的表面积=2 ah+2bh+2ab
【分析】(1)根据几何体的表面展开图的特点解答;
(2)根据侧面积公式计算表面积计算公式解答.
【详解】解:(1)给出三种纸样甲、乙、丙,在甲、乙、丙中,正确的有甲、丙,
故答案为:甲、丙;
(2)如图甲:包装盒的侧面积=(a+b+a+b)h=2ah+2bh;
包装盒的表面积=2ah+2bh+2ab.
.
【点睛】此题考查立方体的表面展开图,立体图形的表面积及侧面积计算公式,正确掌握立体图形的表面展开图的特点是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.3转化表达
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图所示的几何体是由一些小正方体组成的,那么从左边看它的图形是( )
A. B. C. D.
2.下列图形中,可以折叠成三棱柱的是( )
A. B. C. D.
3.在如图所示的图形中是正方体的展开图的有( )
A.3种 B.4种 C.5种 D.6种
4.如图,点A,B,C是正方体三条相邻的棱的中点,沿着A,B,C三点所在的平面将该正方体的一个角切掉,然后将其展开,其展开图可能是( )
A. B. C. D.
5.如图所示的三棱柱的展开图不可能是( )
A. B.
C. D.
6.如图,一个正方体纸盒的六个面上填有不同的数或式,从不同方向看到的情形如图所示,如果相对两个面上的数或式的值互为相反数,则(a+c﹣x)2022的值为( )
A.1 B.﹣1 C.0 D.2022
7.如图是正方体的一种展开图,那么在原正方体中与“我”字所在面相对的面上的汉字是( )
A.大 B.美 C.遂 D.宁
8.下列图形中,能折叠成正方体的是( )
A. B. C. D.
9.如图,有一个无盖的正方体纸盒,下底面标有字母“M”,沿图中粗线将其剪开展成平面图形,想一想,这个平面图形是( )
A. B.
C. D.
10.如图,是正方体的一个平面展开图,如果原正方体上“友”所在的面为前面,则“信”与“国”所在的面分别位于( ).
A.上,下 B.右,后 C.左,右 D.左,后
11.有一正方体,六个面上分别写有数字1、2、3、4、5、6,有三个人从不同的角度观察的结果如图所示.如果记6的对面的数字为a,2的对面的数字为b,那么的值为( )
A.3 B.7 C.8 D.11
12.如图,下面每一组图形都由四个等边三角形组成,其中可以折叠成三棱锥的是( )
A.仅图① B.图①和图② C.图②和图③ D.图①和图③
二、填空题
13.将如图所示的几何体沿虚线折叠,折成的几何体的名称是 .
14.某小组开展“无盖长方形纸盒制作”的综合实践活动,他们准备在一张长为,宽为的长方形纸板上按照如图的方式进行裁剪,剪去阴影部分后,再将剩余纸板沿虚线折合.若,则折合后的无盖纸盒体积为 .
15.如图是一个长方体纸盒表面展开图,纸片厚度忽略不计,按照图中数据,这个长方体盒子容积为 .
16.一个长方体包装盒展开后如图所示(单位:cm),则其容积为 cm3.
17.圆柱的侧面展开图是一个相邻的两边长分别为4,2π的长方形,则圆柱体的体积为 .
三、解答题
18.图中的两个图形经过折叠能否围成棱柱?先想一想,再折一折.
19.如图是一个正方体的平面展开图,标注了字母M的是正方体的前面,标注了﹣2的是正方体的底面,正方体的左面与右面标注的式子的和为21
(1)求x的值;
(2)求正方体的上面和后面的数字的积.
20.下面是一个多面体的表面展开图每个面上都标注了字母,(所有字母都写在这一多面体的外表面)请根据要求回答问题:
(1)如果面在前面,从左边看是,那么哪一面会在上面?
(2)如果从右面看是面面,面在后边那么哪一面会在上面?
(3)如果面在多面体的底部,从右边看是,那么哪一面会在前面.
21.小丽同学周末帮妈妈拆完快递后,将包装盒展开,进行了测量,结果如图所示.已知长方体盒子的长比宽多3cm.
(1)求长方体盒子的长和宽.
(2)求这个包装盒的体积.
22.如图是一个正方体的表面展开图,若正方体中相对的面上的数互为相反数,则、x、y的值分别为多少?
23.如图,在正方体能看到的面上写着1,2,3,而在展开图上已写了2个或1个指定的数,试在展开图的其他各面上写上适当的数,使其相对面上的两数之和为7.
24.有一种牛奶软包装盒如图1所示.为了生产这种包装盒,需要先画出展开图纸样.
(1)如图2给出三种纸样甲、乙、丙,在甲、乙、丙中,正确的有______________.
(2)利用你所选的一种纸样,求出包装盒的侧面积和表面积(侧面积与两个底面积的和)
《5.3转化表达》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B C D D A B C B C
题号 11 12
答案 B D
1.B
【分析】本题考查从不同角度看几何体,得出从左面看几何体得到的图形即可解题.
【详解】解:从左边看它的图形是
,
故选B.
2.B
【分析】本题考查几何体展开图的判断,根据展开图的特点即可判断.
【详解】解:A、根据图形判断是圆锥展开图,不符合题意;
B、根据图形判断是三棱柱展开图,符合题意;
C、根据图形判断是正方体展开图,不符合题意;
D、根据图形判断是四棱锥展开图,不符合题意.
故选:B.
3.C
【分析】根据正方体展开图的11种形式对各小题分析判断即可得解.
【详解】解:由正方体的11种展开图的特征可知,图1、图2、图3、图4、图6都是正方体的展开图,图5出现了“田”字,不能围成正方体.
∴以上是正方体的展开图的有5种.
故选:C.
【点睛】本题考查了正方体的展开图,熟记展开图的11种形式是解题的关键,利用不是正方体展开图的“一线不过四、田凹应弃之”(即不能出现同一行有多于4个正方形的情况,不能出现田字形、凹字形的情况)判断也可.
4.D
【分析】考查了截一个几何体和几何体的展开图.由平面图形的折叠及立体图形的表面展开图的特点解题.
【详解】解:A、折叠后两个剪去三角形与另一个剪去的三角形不交于一个顶点,不符合题意;
B、折叠后两个剪去三角形与另一个剪去的三角形不交于一个顶点,不符合题意;
C、折叠后两个剪去三角形与另一个剪去的三角形不交于一个顶点,不符合题意;
D、折叠后两个剪去三角形与另一个剪去的三角形交于一个顶点,与正方体三个剪去三角形交于一个顶点符合,符合题意.
故选:D.
5.D
【分析】三棱柱的表面展开图的特点,由三个长方形的侧面和上下两个三角形的底面组成.从而可得答案.
【详解】解:选项A、B、C均可能是该三棱柱展开图,不符合题意,
而选项D中的两个底面会重叠,不可能是它的表面展开图,符合题意,
故选:D.
【点睛】考查了几何体的展开图,动手折叠一下,有助于空间想象力的培养.
6.A
【分析】结合图形找出相对面,求出a+c与x的值,代入式子中即可解答.
【详解】解:由图可知:
a+b与c+d为相对面,a b与c d为相对面,x与 1为相对面,
∵相对两个面上的数或式的值互为相反数,
∴a+b= (c+d)①,
a b= (c d)②,
x=1,
∴①+②得:2a= c d c+d,
2a= 2c,
2a+2c=0,
∴a+c=0,
∴(a+c x)2022=(0 1)2022=1,
故选:A.
【点睛】本题考查了正方体相对两个面上的文字,结合图形找出相对面求出a+c与x的值是解题的关键.
7.B
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【详解】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“我”与“美”是相对面.
故选:B.
【点睛】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手.
8.C
【分析】根据正方体展开图的常见形式作答即可.注意只要有“田”“凹”字格的展开图都不是正方体的表面展开图.
【详解】解:A、不能折叠成一个正方体,故选项不符合题意;
B、能折叠成三棱柱,故选项不符合题意;
C、能折叠成一个正方体,故选项正确,符合题意;
D、不能折叠成正方体,故选项不符合题意.
故选:C.
【点睛】本题考查了展开图折叠成几何体.能组成正方体的“一,四,一”“三,三”“二,二,二”“一,三,二”的基本形态要记牢.
9.B
【分析】由平面图形的折叠及正方体的展开图解题.正方体共有11种表面展开图,把11种展开图都去掉一个面得无盖的正方体展开图,把相同的归为一种得无盖正方体有8种表面展开图.
【详解】解:选项A经过折叠后,标有字母“M”的面不是下底面,
选项C折叠后,不是沿图中粗线将其剪开的,
选项D不可能折叠为正方体,
B正确.
故选:B.
10.C
【分析】正方体的平面展开图中,相对的两个面中间必须隔着一个小正方形,根据这一特点,结合题意可正确解答.
【详解】解:如果原正方体上“友”所在的面为前面,则“信”所在的面为左面,
所以相对的正方体的右面是“国”.
故选C.
【点睛】本题考查正方体相对两个面上的文字,解决本题的关键是要熟练掌握正方体展开图形相对两个面上的文字确定的方法.
11.B
【分析】由图一和图二可看出1的对面的数字是5;再由图二和图三可看出3的对面的数字是6,从而2的对面的数字是4.
【详解】解:从3个小立方体上的数可知,
与写有数字1的面相邻的面上数字是2,3,4,6,
所以数字1面对数字5,
同理,立方体面上数字3对6.
故立方体面上数字2对4.
则a=3,b=4,
那么a+b=3+4=7.
故选B.
【点睛】本题考查灵活运用正方体的相对面解答问题,立意新颖,是一道不错的题.解题的关键是按照相邻和所给图形得到相对面的数字.
12.D
【分析】由平面图形的折叠及三棱锥的展开图解题.
【详解】解:只有图①、图③能够折叠围成一个三棱锥.
故选:D.
【点睛】本题考查了展开图折叠成几何体的知识,属于基础题型.
13.三棱柱
【分析】本题考查作图-应用与设计作图.由平面图形的折叠的特点解题.
【详解】解:三个长方形和两个三角形能围成三棱柱,
故,将它折叠能得到三棱柱;
故答案为:三棱柱.
14.
【分析】本题考查了矩形的性质和折叠的性质.设,,则,解得,再根据长方体的体积公式计算即可求解.
【详解】解:如图,
∵,
∴设,,
∴,
∴,
∵,
∴,
解得,
∴,,,
∴折合后的无盖纸盒体积为,
故答案为:.
15.6
【分析】根据题意确定出长方体纸盒的长、宽、高,求出容积即可.
【详解】
底面的宽是,
底面的长是,
长方体的高是1,
长方体盒子容积为:.
故答案为:6.
【点睛】
此题考查了几何体的展开图,找出长方体的长、宽、高是解本题的关键.
16.6600
【分析】根据题意分别求出长方体的长、宽、高,再根据长方体的体积公式计算即可求解.
【详解】解:由题意可得,该长方体的高为:42﹣32=10(cm),宽为:32﹣10=22(cm),长为:(70﹣10)÷2=30(cm),
故其容积为:30×10×22=6600(cm3),
故答案为:6600.
【点睛】本题考查了几何体的展开图,解题的关键是得到长方体的长宽高.
17.4π或8/8或4π
【分析】
分两种情况:①以2π为底面周长,4为高;②以4为圆柱体的底面周长,2π为高;分别求解即可.
【详解】
解:①以2π为底面周长,4为高,
此时圆柱体的底面半径为=1,
∴圆柱体的体积为π×12×4=4π,
②以4为圆柱体的底面周长,2π为高,
此时圆柱体的底面半径为,
∴圆柱体的体积为π×()2×2π=8,
故答案为:4π或8.
【点睛】
本题考查圆柱体的展开与折叠,理解圆柱体表面展开图与圆柱体之间的关系是解决问题的关键.
18.(1)能围成三棱柱;(2)不能围成棱柱.
【分析】分别利用已知平面展开图进而分析得出答案.
【详解】解:如图(1)可以折成三棱柱,
如图(2)不能折成棱柱.
【点睛】本题主要考查展开图折叠成几何体的知识点,熟记常见立体图形的平面展开图是解决此类问题的关键.
19.(1)x=3
(2)-9
【分析】(1)正方体的表面展开图,相对的面之间一定相隔一个正方形确定出相对面,然后列出方程求解即可;
(2)确定出上面和底面上的两个数字-2和-3,然后相加即可.
【详解】(1)解:由正方体表面展开图的“相间、Z端是对面”可知,
“x”与“M”是相对的面,
“﹣2”与“﹣3”是相对的面,
“4x”与“2x+3”是相对的面,
又因为标注了字母M的是正方体的前面,标注了﹣2的是正方体的底面,
所以标注了字母x的是正方体的后面,标注了﹣3的是正方体的上面,
因此标注“4x”与“2x+3”是左面和右面,
又因为正方体的左面与右面标注的式子的和为21,
所以4x+2x+3=21,
解得x=3;
(2)解:因为标注了字母x的是正方体的后面,标注了﹣3的是正方体的上面,而x=3,
所以正方体的上面和后面的数字的积为﹣3×3=﹣9.
【点睛】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题是解题的关键.
20.(1)面会在上面;(2)面会在上面;(3)面会在前面
【分析】利用长方体及其表面展开图的特点解题.这是一个长方体的平面展开图,共有六个面,其中面“A”与面“F”相对,面“B”与面“D”相对,面“C”与面“E”相对.
【详解】解:(1)由图可知,如果F面在前面,B面在左面,那么“E”面下面,∵面“C”与面“E”相对,∴C面会在上面;
(2)由图可知,如果C面在右面,D面在后面,那么“F”面在下面,∵面“A”与面“F”相对,∴A面在上面.
(3)由图可知,如果面在多面体的底部,从右边看是,那么“E”面在后面,∵面“C”与面“E”相对,∴ 面会在前面
【点睛】考查了几何体的展开图,注意正方体的空间图形,从相对面入手,分析及解答问题.
21.(1)长方体盒子的长为,宽为;
(2)这个包装盒的体积是.
【分析】本题考查了长方体的展开图,关键是得到长方体的长,宽,高.
(1)要求长方体的体积,需知长方体的长,宽,高,结合图形可知2个宽2个高20,依此可求长方体盒子的宽;再根据长方体盒子的长宽3,可求长方体盒子的长;
(2)根据长方体的体积公式即可求解.
【详解】(1)解:长方体盒子的宽为,
长方体盒子的长为,
答:长方体盒子的长为,宽为;
(2)解:这个包装盒的体积为.
答:这个包装盒的体积是.
22.,,
【分析】本题主要考查的是正方体相对面上的文字,相反数的定义.根据正方体的展开图中可得“y”与“x”是对面,“5”与“”是对面,从而可根据相反数的定义求得x的值及y的值.
【详解】解:∵“y”与“x”是对面,“5”与“”是对面,正方体中相对的面上的数互为相反数,
∴,,
解得.
23.见解析
【分析】先确定数1、2、3所在面的相对面上的数,再根据正方体的展开图特点即可得.
【详解】由题意得:数1所在面的相对面上的数为,
数2所在面的相对面上的数为,
数3所在面的相对面上的数为,
则填图如下:
【点睛】本题考查了正方体的展开图,熟练掌握正方体的展开图特点是解题关键.
24.(1)甲、丙;(2)侧面积=2ah+2bh;包装盒的表面积=2 ah+2bh+2ab
【分析】(1)根据几何体的表面展开图的特点解答;
(2)根据侧面积公式计算表面积计算公式解答.
【详解】解:(1)给出三种纸样甲、乙、丙,在甲、乙、丙中,正确的有甲、丙,
故答案为:甲、丙;
(2)如图甲:包装盒的侧面积=(a+b+a+b)h=2ah+2bh;
包装盒的表面积=2ah+2bh+2ab.
.
【点睛】此题考查立方体的表面展开图,立体图形的表面积及侧面积计算公式,正确掌握立体图形的表面展开图的特点是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
