2026年中考《数学》复习课件：专题二 方程（组）与不等式（组）-第6讲 一元一次方程和二元一次方程组（55张PPT）

(共55张PPT)
复习讲义
第一篇 吃透考点
专题二 方程（组）与不等式（组）
1.传统文化（2024·广西·中考第11题）《九章算术》是我国古代重要的
数学著作，其中记载了一个问题，大致意思为：现有田出租，第一年3
亩1钱，第二年4亩1钱，第三年5亩1钱.三年共得100钱.问：出租的田有
多少亩？设出租的田有 亩，可列方程为( ).
（1亩 ，钱：古代货币单位）
B
A. B.
C. D.
2.（2024·怀化·中考第16题）不等式 的解集为________.
3.（2023·安徽·中考第20题）解分式方程： .
解：去分母，得.移项，得.所以 .检验：当
时，.所以原分式方程的解为 .
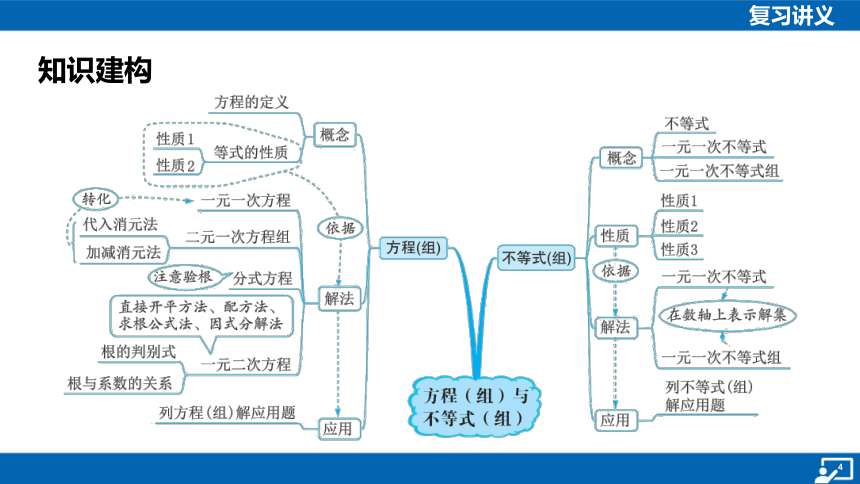
知识建构
第6讲 一元一次方程和二元一次方程组
聚焦核心
1.等式的性质
性质1：如果，那么 ______．
性质2：如果，那么 ____；
如果，那么__ ．
2.一元一次方程
（1）定义：只含有____个未知数（元），未知数的次数都是___，等号
两边都是整式，这样的方程叫作一元一次方程．
（2）解一元一次方程的步骤：去分母、________、______、_________
___、未知数系数化为1．
一
1
去括号
移项
合并同类项
3.二元一次方程组
（1）二元一次方程：含有____个未知数（元），并且含有未知数的项
的次数都是___，这样的方程叫作二元一次方程．
两
1
（2）二元一次方程组：把两个含有______未知数的二元一次方程
（或一个二元一次方程，一个一元一次方程）联立起来，组成的方程组
叫作二元一次方程组.
相同
（3）二元一次方程的解：使二元一次方程左、右两边的值______的两
个未知数的值，叫作二元一次方程的解．
相等
说明：一般来说，一个二元一次方程有无数组解．
（4）二元一次方程组的解：二元一次方程组的两个方程的________，
叫作二元一次方程组的解．
（5）解二元一次方程组的方法：______消元法和______消元法．
公共解
代入
加减
说明：解二元一次方程组的基本思想是“消元”，通过消元，将“二元”转
化为“一元”．
4.列方程（组）解应用题的步骤
（1）审：审清题意，找到等量关系.
（2）设：设未知数（可直接设未知数，也可间接设未知数）.
（3）列：根据等量关系列出方程（组）.
（4）解：解方程（组）.
（5）验：检验未知数的值是否正确，是否符合题意.
（6）答：完整地写出答句，注意单位名称.
5.常见的几种方程类型及等量关系
（1）行程问题中的基本量之间的关系：
路程 速度×时间．
①相遇问题：相遇时两者所走的路程之____ 出发时两者之间的距离；
②追及问题：追上时两者所走的路程之____ 出发时两者之间的距离；
③流水问题：
， ．
和
差
（2）工程问题：工作效率 ．
注意：通常将工作总量看作“1”．
（3）利润问题：
①售价 标价×折扣；
②销售额 售价×销量；
③利润 售价 进价（成本价）；
④利润率 ．
（4）储蓄问题:
①利息 本金×利率×期数；
②本息和本金利息本金（利率 期数）．
（5）计费问题：
①总价 ______×数量；
②分段计费：总费用第1分段单价×数量第2分段单价×数量 第
分段单价×数量.
单价
第6讲 一元一次方程和二元一次方程组
案例分析
考点一 一元一次方程及其解法
名师指导
解一元一次方程，要注意：
（1）去分母时，不要漏乘没有分母的项；
（2）去括号时，不要漏乘括号内的任何一项；
（3）移项时，注意变号；
（4）系数化为1时，不要颠倒分子与分母.
例1 下面是圆圆解一元一次方程 的过程.
解：去分母，得 .
去括号，得 .
移项、合并同类项，得 .
系数化为1，得
圆圆的解答过程是否有错误？如果有错误，那么请写出正确的解答过程.
思路点拨 根据一元一次方程的解法，逐步检查，作出判断.
解：圆圆的解答有错，正确解答过程如下：
去分母，得.
去括号，得 .
移项、合并同类项，得.系数化为1，得 .
考点专练
1.（2023·湖南永州·中考）关于的一元一次方程 的解为
，则 的值为( ).
A
A.3 B. C.7 D.
2.一元一次方程的解是 ___.
1
3.解一元一次方程：
（1） ;
解：去括号，得.移项，得 .合并同
类项，得.系数化为1，得 .
（2） .
解：去分母，得.
去括号，得3.
移项、合并同类项，得.
系数化为1，得.
考点二 二元一次方程（组）及其解法
名师指导
解二元一次方程组时，代入消元法和加减消元法的适用情况如下：
（1）当方程组中有一个方程的一个未知数的系数为1或时，选
择代入消元法较简单.
（2）当方程组中同一个未知数的系数相等，或互为相反数，或成
整数倍关系时，选择加减消元法较简单.
例2 开放性题（2023·四川泸州·中考）关于， 的二元一次方程组
的解满足，写出 的一个整数值_________.
思路点拨 要写出的一个整数值，就要先求出的取值范围.求 的取值
范围有以下两种思路：（思路一）把看作常数解方程组，再将用含 的
代数式表示的，的值代入，解不等式即可得到 的取值范
围.（思路二）根据方程组中 的系数特点，将第一个方程减去第二个方
程得到，代入，求解不等式即可得到 的取值
范围.
【解析】一题多解 提示：已知求 的取值范围有以
下两种方法：
（方法一）得.将 代入②，解得
.因为，所以 .解得
.
（方法二），得．因为 ，所以
.解得 .
因为，所以.所以.要取 的一
个整数值，只要大于5即可．
答案：6（答案不唯一）
考点专练
4.（2023·江苏无锡·中考）下列四组数中，不是二元一次方程
的解的为( ).
D
A. B. C. D.
5.（2023·四川眉山·中考）已知关于, 的二元一次方程组
的解满足，则 的值为( ).
B
A.0 B.1 C.2 D.3
提示：将方程组的两个方程相减，整理得.因此 .
解得 .
6.解二元一次方程组：
（1）（2024·广西玉林·模拟）
解：将②代入①，得.
解得.
将代入②，得.
因此原方程组的解是
（2）（2023·泸州·中考）
解：，得.
解得.
将代入①，得.
解得.
因此原方程组的解是
（3）
解：，得.
解得.
将代入①，得3.
解得.
因此原方程组的解是
考点三 一元一次方程和二元一次方程（组）的应用
名师指导
解一次方程（组）的应用问题的关键是正确分析题目中的相关数据，
找到列方程（组）的等量关系.列一元一次方程,需要找到一个等量关系;
列二元一次方程组，需要找到两个等量关系. 一些应用问题既可以用二
元一次方程组求解，也可以用一元一次方程求解.
例3 （2024·湖州·中考）某村决定种植脐橙和黄金贡柚，助推村民增收
致富.已知购买1棵脐橙树苗和2棵黄金贡柚树苗共需110元，购买2棵脐橙
树苗和3棵黄金贡柚树苗共需190元.
（1）求脐橙树苗和黄金贡柚树苗的单价.
思路点拨（1）题设中有两个未知量，可设出两个未知数，根据等量关
系“购买1棵脐橙树苗的费用购买2棵黄金贡柚树苗的费用 元”“购
买2棵脐橙树苗的费用购买3棵黄金贡柚树苗的费用 元”可列二元
一次方程组求解.
解：设脐橙树苗的单价为元，黄金贡柚树苗的单价为 元.
由题意，得
解得
答：脐橙树苗的单价为50元，黄金贡柚树苗的单价为30元.
（2）该村计划购买脐橙树苗和黄金贡柚树苗共1 000棵，总费用不超过
38 000元，问最多可以购买脐橙树苗多少棵？
解：设可以购买脐橙树苗棵，则购买黄金贡柚树苗棵.
由题意，得.
解得.
答：最多可以购买脐橙树苗400棵．
思路点拨（2）根据总费用不超过38 000元，列出一元一次不等式，解不等式即可.
考点专练
7.数学文化（2024·江苏无锡·中考）《九章算术》中有一道“凫雁相逢”
问题（凫：野鸭），大意如下：野鸭从南海飞到北海需要7天，大雁从
北海飞到南海需要9天.如果野鸭、大雁分别从南海、北海同时起飞，那
么经过多少天它们相遇？设经过 天它们相遇，则下列方程正确的是
( ).
A
A. B. C. D.
8.数学文化（2024·广东深圳·中考改编）在明朝程大位编写的《算法统
宗》中有一首住店诗：我问开店李三公，众客都来到店中，一房七客多
七客，一房九客一房空.诗的大意是：一些客人到李三公的店中住宿，
如果每间客房住7人，那么有7人无房可住；如果每间客房住9人，那么
刚好空出1间房.设该店有客房间，房客 人，则可列方程组为
_ _____________.
9.（2024·江苏连云港·中考）某市将5月21日设立为该市“人才日”，以最
大诚意礼遇人才，让人才与城市“双向奔赴”.活动主办方分两次共邮购了
200把绘有西游文化的折扇作为当天一项活动的纪念品.折扇单价为8元，
其中邮费和优惠方式如下表：
邮购数量 把 100把以上（含100把）
邮寄费用 总价的 免费邮寄
折扇价格 不优惠 打九折
已知两次邮购折扇共花费1 504元，求两次各邮购了多少把折扇？
解：（方法一）若每次购买都是100把，则2．
所以两次邮购折扇中有一次邮购少于100把，另一次邮购多于100把．
设一次邮购折扇把，则另一次邮购折扇把．
由题意，得8.
解得．
所以2．
答：两次分别邮购了40把和160把折扇．
（方法二）同方法一可得两次邮购折扇中有一次邮购少于100把，另一次邮购多于100把．
设一次邮购折扇 把，另一次邮购折扇把．
由题意，得
解得
答：两次分别邮购了40把和160把折扇．
第6讲 一元一次方程和二元一次方程组
靶向锤炼
靶向练
1.教材变式［湘教版七上第108页第1题变式］下列各式变形正确的是
( ).
A
A.若，则 B.若，则
C.若，则 D.若，则
2.（2023·江苏无锡·中考）下列四组数中，不是二元一次方程
的解的为( ).
D
A. B. C. D.
3.数学文化（2024·广西北海·模拟）《希腊文选》中有一道数学家欧几
里得编的数学题：驴和骡子驮着若干袋的货物并排走在路上，驴忍不住
埋怨自己驮的货物太重，压得受不了.骡子对驴说：“我驮的货物比你重，
若你的货物给我一袋，我驮的货物则是你驮的两倍，而我给你一袋，咱
俩驮的才一样多.”假设驴驮的货物有袋，骡子驮的货物有 袋，则下列
二元一次方程组正确的是( ).
A
A. B.
C. D.
4.数学文化（2023·辽宁大连·中考）我国重要数学著作《九章算术》中
记载了这样一道题：今有共买物，人出八，盈三；人出七，不足四.问
有几人？其大意是：今有人合伙购物，每人出8钱，会多3钱；每人出7
钱，又差4钱.问人数有多少.设有 人，则可列方程为________________.
（“钱”为当时的计量单位）
5.解下列方程（组）
（1）（2024·广西柳州·模拟）
；
解：去括号，得.
移项，得.
合并同类项，得.
系数化为1，得.
（2）（2024·广西柳州·模拟）
（方法一），得.解得.
将 代入②，得.
解得.因此原方程组的解为
（方法二）由②，得.
将③代入①，得 .解得.
将代入③，得.
因此原方程组的解为
6.跨学科题（2024·吉林·中考）钢琴素有“乐器之王”的美称，键盘上有
白色琴键和黑色琴键共88个，白色琴键比黑色琴键多16个.求白色琴键
和黑色琴键的个数.
解：设黑色琴键有个，则白色琴键有个.
由题意，得.
解得.
所以白色琴键有（个）.
答：白色琴键有52个，黑色琴键有36个．
攻坚练
7.跨学科题（2024·贵州·中考）小红学习了等式的性质后，在甲、乙两
台天平的左右两边分别放入“”“●”“ ”三种物体，如图1所示，天平都
保持平衡.若设“”与“●”的质量分别为， ，则下列关系式正确的是
( ).
图1
A. B. C. D.
提示：设“”的质量为．根据甲天平，得 ；根据乙天
平，得.将①的两边同时减，得 ；将②的两边
同时减，得；将④的两边同时乘2，得.所以 ．
图1
【答案】C
8.（2023·广西百色·模拟）关于，的方程组 的解为
若点在直线上方，则 的取值范围是( ).
A
A. B. C. D.
提示：将方程组的两个方程相减，得 .所以
.因为点在直线上方，所以 ，即
.所以.解得 .
9.数学文化（2024·四川宜宾·中考）元朝朱世杰所著的《算学启蒙》中，
记载了这样一道题：良马日行二百四十里，驽马日行一百五十里，驽马
先行一十二日，问良马几何日追及之？其大意是：快马每天行240里，
慢马每天行150里，慢马先行12天，问快马几天可追上慢马？快马追上
慢马的天数是( ).（“里”为当时的计量单位，1里 ）
D
A.5 B.10 C.15 D.20
10.（2024·四川宜宾·中考）某果农将采摘的荔枝分装为大箱和小箱销售，
其中每个大箱装荔枝，每个小箱装荔枝.该果农现采摘 荔枝，
根据市场销售需求，大小箱都要装且都装满，则所装的箱数最多为
( ).
A.8箱 B.9箱 C.10箱 D.11箱
提示：设用个大箱，个小箱.根据题意，得 .所以
.这个方程的正整数解为或 故所装的箱
数最多为 （箱）．
C
11.（2024·江苏宿迁·中考）如果关于， 的二元一次方程组
的解是那么关于，的方程组
的解是_ ________.
提示：将方程组整理得 则
，.解得， .
12.解下列方程（组）
（1） ;
解：去分母，得.
移项，得.
合并同类项，得.
系数化为1，得.
（2）（2023·内蒙古呼和浩特·中考）
解：整理，得，得.解得.
将代入①，得.
解得.
因此原方程组的解是
13.（2024·安徽·中考）乡村振兴战略实施以来，很多外出人员返乡创业.
某村有部分返乡青年承包了一些田地，采用新技术种植A，B两种农作
物.种植这两种农作物每公顷所需人数和投入资金如下表：
农作物品种 每公顷所需人数 每公顷所需 投入资金（万元）
A 4 8
B 3 9
已知农作物种植人员共24名，且每人只参与一种农作物种植，投入
资金共60万元.问A，B这两种农作物的种植面积各多少公顷？
解：农作物的种植面积为，B农作物的种植面积为 .
根据题意，得
解得
答：A农作物的种植面积为 ，B农作物的种植面积为 ．
拔尖练
图2
14.传统文化（2023·北京·中考）对联是中华传统文化的
瑰宝.对联装裱后，如图2所示，上、下空白处分别称为
天头和地头，左、右空白处统称为边．一般情况下，天
头长与地头长的比是 ，左、右边的宽相等，均为天
头长与地头长的和的 ．某人要装裱一副对联，对联的
长为，宽为 ．要求装裱后的长是装裱后的宽的4倍，求边
的宽和天头长．
图2
解：设天头长为，地头长为，则左、右边的宽为.
根据题意，得1.
解得.
答：边的宽为，天头长为．