(基础篇)2024-2025学年下学期小学数学人教版五年级暑假分层作业第七单元《折线统计图》(含解析)
文档属性
| 名称 | (基础篇)2024-2025学年下学期小学数学人教版五年级暑假分层作业第七单元《折线统计图》(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 410.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 20:45:22 | ||
图片预览

文档简介
(基础篇)2024-2025学年下学期小学数学人教版五年级暑假分层作业第七单元《折线统计图》
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.想要知道某市2024年5月份的气温变化情况,要搜集的数据是( )。
A.2024年各个季度平均气温 B.2024年各月平均气温
C.2024年5月每天的平均气温 D.2024年5月1日各时刻的气温
2.要比较凉山州2024年4月、5月的气温变化情况,绘制( )统计图更合理。
A.单式条形 B.复式条形 C.单式折线 D.复式折线
3.下面情形适合用折线统计图表示的是( )。
A.商场内空调、风扇、吹风机的销售情况
B.班级中喜欢吃香蕉、苹果、桔子、荔枝的人数
C.一天的气温变化情况
4.星期天,小红和妈妈从家出发步行到离家的公园,用时15分钟,在公园玩了半个小时,然后乘出租车回到家里,用时5分钟,下面图( )描述的是小红和妈妈的离家时间和离家距离的关系。
A. B. C.
5.下列说法中,正确的是( )。
A.把5米长的绳子分成8段,每段长米
B.因为18÷6=3,所以18是倍数,6和3是因数
C.两个质数的和一定是偶数
D.要表示出某商场去年每月销售量的变化情况,选用折线统计图比较合适
二、填空题
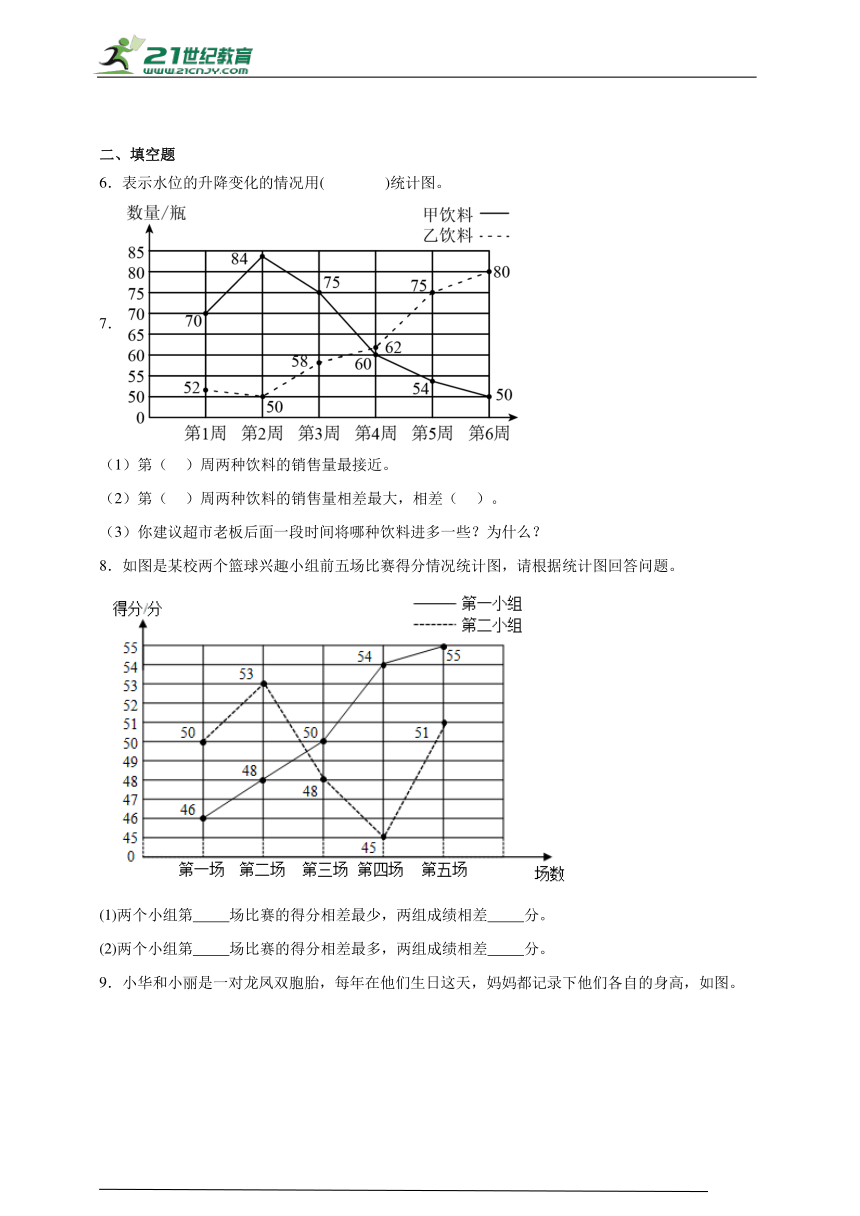
6.表示水位的升降变化的情况用( )统计图。
7.
(1)第( )周两种饮料的销售量最接近。
(2)第( )周两种饮料的销售量相差最大,相差( )。
(3)你建议超市老板后面一段时间将哪种饮料进多一些?为什么?
8.如图是某校两个篮球兴趣小组前五场比赛得分情况统计图,请根据统计图回答问题。
(1)两个小组第 场比赛的得分相差最少,两组成绩相差 分。
(2)两个小组第 场比赛的得分相差最多,两组成绩相差 分。
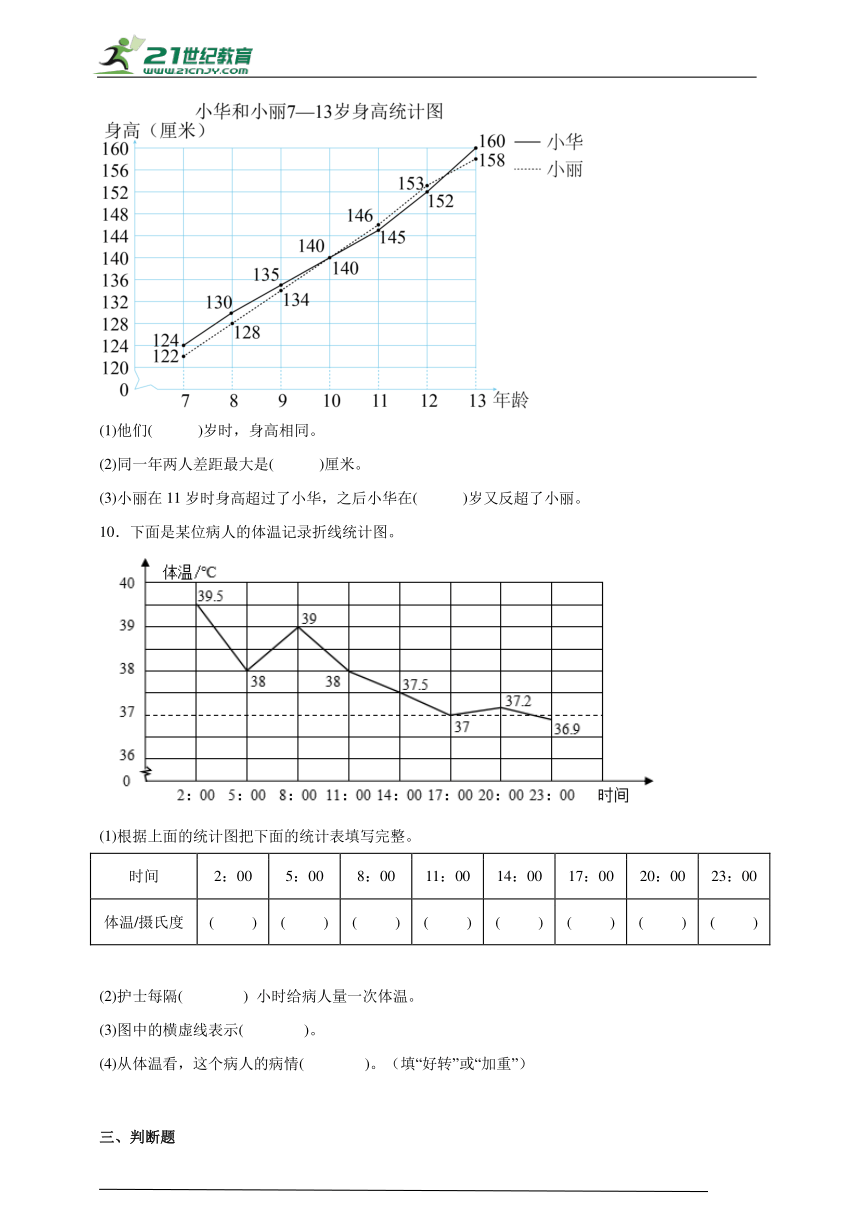
9.小华和小丽是一对龙凤双胞胎,每年在他们生日这天,妈妈都记录下他们各自的身高,如图。
(1)他们( )岁时,身高相同。
(2)同一年两人差距最大是( )厘米。
(3)小丽在11岁时身高超过了小华,之后小华在( )岁又反超了小丽。
10.下面是某位病人的体温记录折线统计图。
(1)根据上面的统计图把下面的统计表填写完整。
时间 2:00 5:00 8:00 11:00 14:00 17:00 20:00 23:00
体温/摄氏度 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
(2)护士每隔( ) 小时给病人量一次体温。
(3)图中的横虚线表示( )。
(4)从体温看,这个病人的病情( )。(填“好转”或“加重”)
三、判断题
11.折线统计图不仅便于直观了解数量的多少,还可以反映数量的增减变化。( )
12.如果要统计某地年至年每年新生婴儿不同性别人数变化情况,应制成复式折线统计图。( )
13.气象局要统计今年上半年每月的降水量变化情况,一般会绘制条形统计图。( )
14.要清楚地表示一个病人的体温变化情况,用折线统计图较好。( )
15.复式折线统计图是用图例区别事物的。( )
16.小明发烧了,妈妈想记录小明一天的体温,选用折线统计图记录较合适。( )
四、计算题
17.计算下面各题,能简算的要简算。
(1) (2) (3) (4)
五、解答题
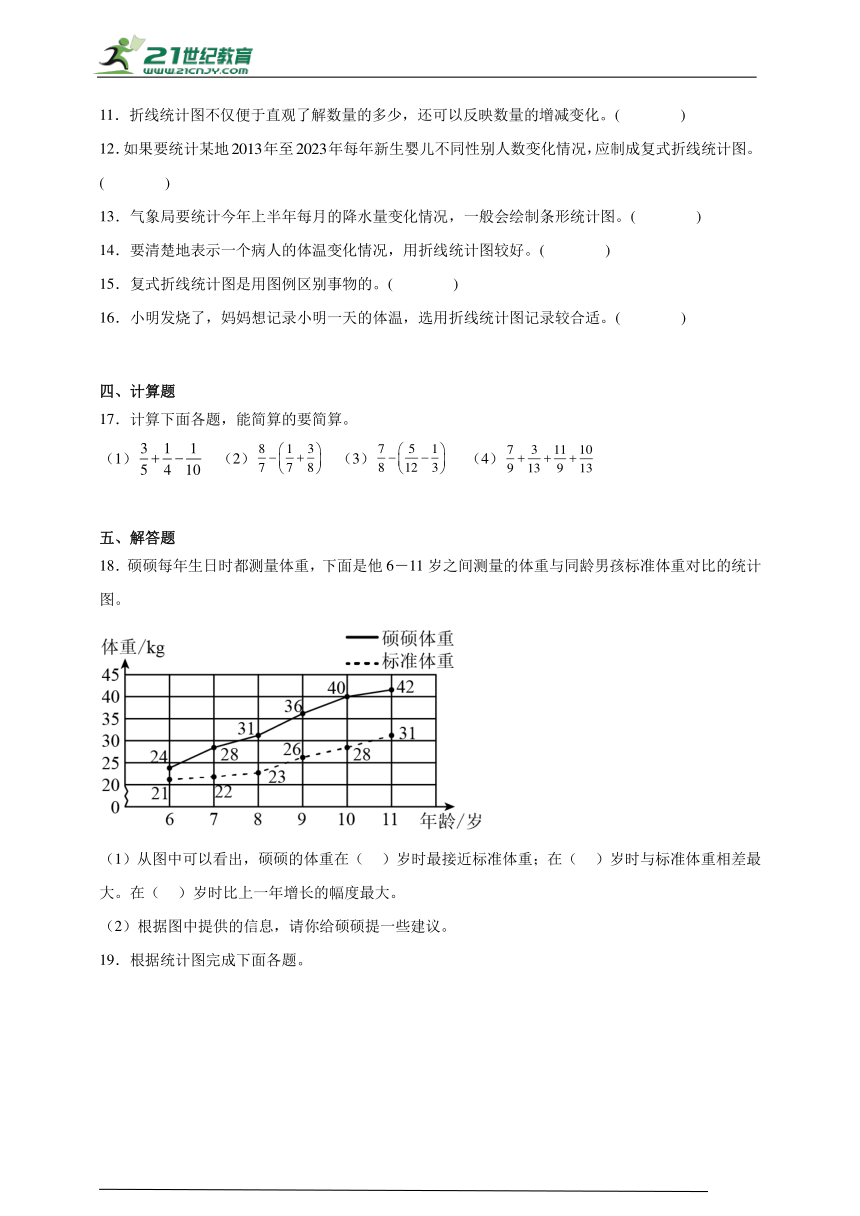
18.硕硕每年生日时都测量体重,下面是他6-11岁之间测量的体重与同龄男孩标准体重对比的统计图。
(1)从图中可以看出,硕硕的体重在( )岁时最接近标准体重;在( )岁时与标准体重相差最大。在( )岁时比上一年增长的幅度最大。
(2)根据图中提供的信息,请你给硕硕提一些建议。
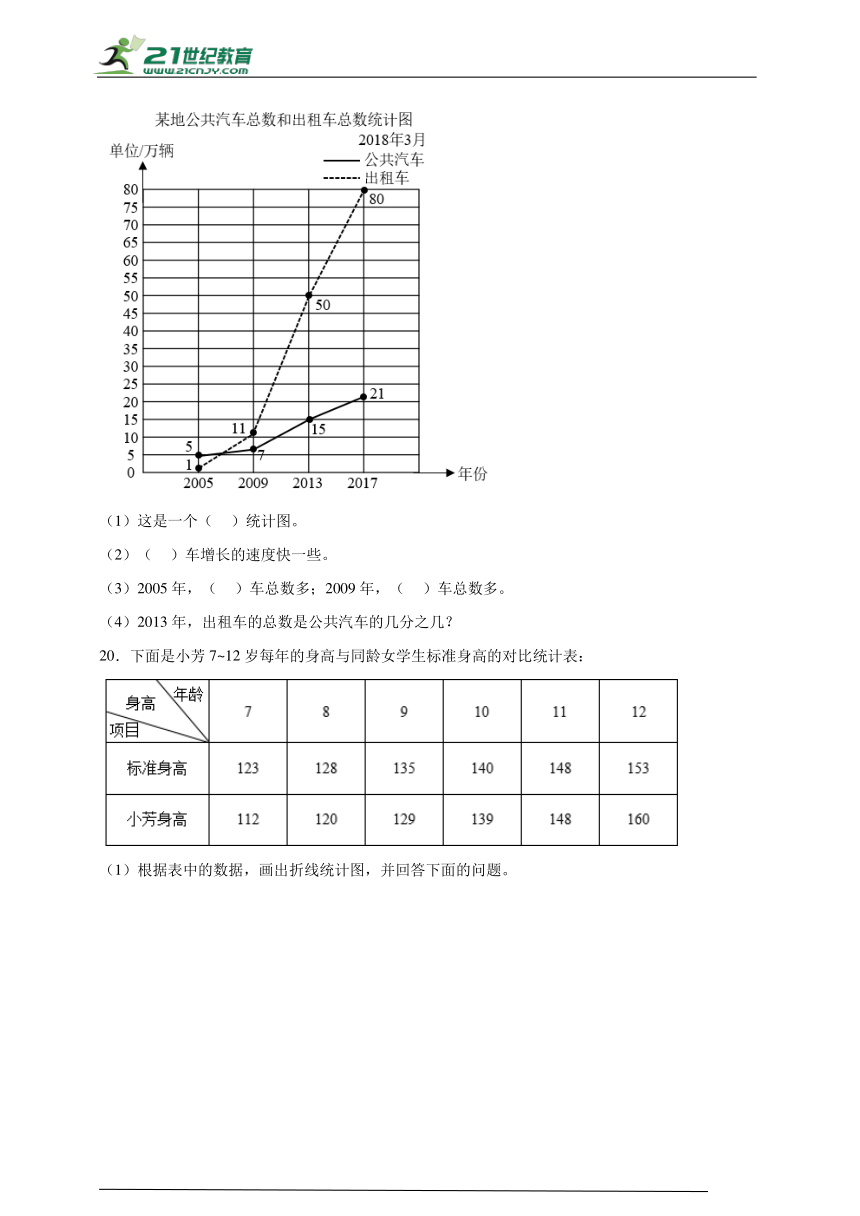
19.根据统计图完成下面各题。
(1)这是一个( )统计图。
(2)( )车增长的速度快一些。
(3)2005年,( )车总数多;2009年,( )车总数多。
(4)2013年,出租车的总数是公共汽车的几分之几?
20.下面是小芳7~12岁每年的身高与同龄女学生标准身高的对比统计表:
(1)根据表中的数据,画出折线统计图,并回答下面的问题。
(2)小芳从( )岁到( )岁身高增长得最快。
(3)对比标准身高,小芳7~12岁身高在11岁之前偏( )(填高或矮)。
《(基础篇)2024-2025学年下学期小学数学人教版五年级暑假分层作业第七单元《折线统计图》》参考答案
题号 1 2 3 4 5
答案 C D C A D
1.C
【分析】根据题意,要知道的是某市2024年5月份的气温变化情况,那么搜集的数据应该能够反映出这个月内气温的每日变化,而不是某个时间点或更长时间段的数据。
【详解】A.2024年各个季度平均气温,一年有4个季度,各个季度的数据范围太大了,无法具体看出5月份的气温变化情况,不符合题意;
B.2024年各月平均气温,一年有12个月,可以看出不同月份的平均气温,但不是5月份的气温变化情况,不符合题意;
C.2024年5月每天的平均气温,每天的数据能详细展示一个月内气温的变化情况,符合题意;
D.2024年5月1日各时刻的气温,只能看出这一天的气温变化,无法反映整个月的情况,不符合题意。
故答案为:C
2.D
【分析】单式条形统计图可以清楚地看出数量的多少。
复式条形统计图可以用不同的条形表示两种以上的量的多少。
单式折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况。
复式折线统计图通过两组以上数据的水平进行比较,可以容易地比较出两组以上数据的变化趋势,更清楚看出各类之间的比较。
【详解】要比较凉山州2024年4月、5月的气温变化情况,绘制复式折线统计图更合理。
故答案为:D
3.C
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;由此根据情况选择即可。
【详解】A.要统计商场内空调、风扇、吹风机的销售情况,用条形统计图较为合适;
B.要统计班级中喜欢吃香蕉、苹果、桔子、荔枝的人数,用条形统计图较为合适;
C.要统计一天的气温变化情况,用折线统计图较为合适。
故答案为:C
【点睛】此题应根据条形统计图、折线统计图各自的特点进行解答。
4.A
【分析】根据题意,小红和妈妈从家出发步行到离家的公园,用时15分钟,这时时间和离家距离都在增加;在公园玩了半个小时,时间又过去30分钟,但离家距离不变;然后乘出租车回到家里,用时5分钟,此时时间在增加,但离家距离不断减少,直至0m。据此逐项分析。
【详解】A。图中小红和妈妈从家出发步行到离家的公园,用时15分钟,之后在公园玩从15分钟到45分钟,玩了45-15=30(分钟),即半个小时,然后乘出租车回到家里,用时50-45=5(分钟),符合题意;
B.图中小红和妈妈从家出发步行到离家的公园,用时15分钟,然后直接乘出租车回到家里,用时20-15=5(分钟),不符合题意;
C.图中小红和妈妈从家出发步行到离家的公园,用时15分钟,之后在公园玩从15分钟到50分钟,玩了50-15=35(分钟),然后乘出租车回到家里,用时55-50=5(分钟),不符合题意。
故答案为:A
5.D
【分析】A.用绳子的长度除以平均分成的段数即可求出每段具体的长度;
B.在整数除法中,商是整数且没有余数,我们就说被除数是除数和商的倍数,除数和商是被除数的因数,因数和倍数是相互依存的,单独的一个数的不能说是因数或倍数;
C.一个自然数如果只有1和它本身两个因数,那么这个自然数叫做质数;是2的倍数的数叫做偶数;据此举例判断即可;
D.条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;据此判断即可。
【详解】A.把5米长的绳子分成8段,因为题干中并没有说明是平均分,所以不能求出每段的长度,原题干说法错误;
B.因为18÷6=3,所以18是6和3的因数,6和3是18的因数,原题干说法错误;
C.如:2和3都是质数,2+3=5,5是奇数,所以两个质数的和不一定是偶数,原题干说法错误;
D.要表示出某商场去年每月销售量的变化情况,选用折线统计图比较合适,说法正确。
故答案为:D
【点睛】本题考查因数和倍数,明确因数和倍数的定义是解题的关键。
6.折线
【分析】条形统计图可以清楚地看出数量的多少;
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况。
【详解】表示水位的升降变化的情况用折线统计图。
【点睛】理解掌握条形统计图、折线统计图的特点是选择统计图的关键。
7.(1)4
(2)2;34瓶
(3)老板多进一些乙种饮料,因为乙种饮料的销量逐渐上升。(答案不唯一,合理即可)
【分析】(1)黑色实线表示的是甲饮料的销售数量变化,黑色虚线表示的是乙饮料的销售数量变化,当两个变化曲线最接近的时候就是两种饮料销售数量最接近的时候,也就是第四周时候两种饮料销量最接近。
(2)黑色实线和黑色虚线距离最远的时候就是两种饮料相差最多时候,第二周甲销售84瓶,乙销售50瓶,所以相差34瓶。
(3)老板多进一些乙种饮料,因为乙种饮料的销量逐渐上升。(答案不唯一,合理即可)
【详解】(1)第4周两种饮料的销量最接近;
(2)第2周两种饮料的销售量相差最大,相差34瓶;
(3)老板多进一些乙种饮料,因为乙种饮料的销量逐渐上升。(答案不唯一,合理即可)
【点睛】主要考查折线统计图的相关知识,能够正确的认识折线统计图。
8.(1) 三 2
(2) 四 9
【分析】(1)观察折线统计图,实线代表第一小组的前五场比赛得分,虚线代表第二小组的前五场比赛得分,实线和虚线上点与点之间的位置相差最近的时候,即是两个小组比赛的得分相差最少的场次,找到此时对应的场次;并用这个场次中两个小组的得分相减即可;
(2)观察折线统计图,实线代表第一小组的前五场比赛得分,虚线代表第二小组的前五场比赛得分,实线和虚线上点与点之间的位置相差最远的时候,即是两个小组比赛的得分相差最多的场次,找到此时对应的场次;并用这个场次中两个小组的得分相减即可。
【详解】(1)两个小组第三场比赛的得分相差最少;
50-48=2(分)
即两组成绩相差2分。
(2)两个小组第四场比赛的得分相差最多;
54-45=9(分)
即两组成绩相差9分。
【点睛】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
9.(1)10
(2)2
(3)13
【分析】(1)折线统计图中横轴表示年龄,纵轴表示身高,实线表示小华的身高变化,虚线表示小丽的身高,两条线相交的地方就是身高相等,对应的横轴就是年龄,据此可得出答案。
(2)同一年年龄差距最大的,是两条虚线同一个横坐标上纵坐标的差距最大,据此得出答案。
(3)小华身高超过小丽的身高,即实线超过虚线的横坐标,据此得出答案。
【详解】(1)他们10岁时,身高相同。
(2)同一年两人差距最大是2厘米。
(3)小丽在11岁时身高超过了小华,之后小华在13岁又反超了小丽。
10.(1) 39.5 38 39 38 37.5 37 37.2 36.9
(2)3
(3)正常体温
(4)好转
【分析】(1)从折线统计图中读出各个时间点的体温,再填入统计表中即可。
(2)根据折线统计图的横轴可知,护士每隔3小时给病人量一次体温。
(3)折线统计图的横虚线是37℃,表示正常体温。
(4)根据折线统计图可知,这个病人的体温呈逐渐下降趋势,接近正常体温,说明病情好转。
【详解】(1)
时间 2:00 5:00 8:00 11:00 14:00 17:00 20:00 23:00
体温/摄氏度 39.5 38 39 38 37.5 37 37.2 36.9
(2)护士每隔3小时给病人量一次体温。
(3)图中的横虚线表示正常体温。
(4)从体温看,这个病人的病情好转。
【点睛】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
11.√
【详解】折线统计图不仅便于直观了解数量的多少,还可以反映数量的增减变化,说法正确。
故答案为:√
12.√
【分析】根据复式折线统计图的特征:可以同时显示多组数据,清晰的反映变化趋势,易于比较数据差异即可解答。
【详解】因为要统计某地年至年每年新生婴儿不同性别人数变化情况,所以适合用复式折线统计图反映其变化情况。
故答案为:√。
【点睛】本题考查了复式折线统计图的特征:可以同时显示多组数据,清晰的反映变化趋势,易于比较数据差异,熟记复式统计图的特征是解题的关键。
13.×
【分析】折线统计图用折线的起伏表示数据的增减变化情况。不仅可以表示数量的多少,而且可以反映数据的增减变化情况。条形统计图的特点是易于比较数据之间的差别,能清楚地表示出数量的多少。依此判断。
【详解】根据分析可知,气象局要统计今年上半年每月的降水量变化情况,一般会绘制折线统计图。
故答案为:×
【点睛】解答此题的关键是在于掌握折线统计图、条形统计图的特点。
14.√
【分析】条形统计图可以清楚地看出数量的多少;
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况。
【详解】要清楚地表示一个病人的体温变化情况,用折线统计图较好。
原题说法正确。
故答案为:√
【点睛】理解掌握条形统计图、折线统计图的特点是选择统计图的关键。
15.√
【分析】复式折线统计图表示2个及以上的量的增减变化情况,必须通过图例进行区别。
【详解】由分析可知:
复式折线统计图是用图例区别事物的。原题干说法正确。
故答案为:√
【点睛】本题考查了复式折线统计图,复式条形统计图也得通过图例进行区别。
16.√
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;由此根据情况选择即可。
【详解】由分析可得:小明发烧了,妈妈想记录小明一天的体温,选用折线统计图记录较合适,原题说法正确。
故答案为:√
17.(1);(2);(3);(4)3
【分析】(1)先通分把异分母的分数化成同分母的分数,再按照同分母分数加、减法的计算方法进行计算。
(2)先根据减法的性质去括号,再计算同分母分数的减法,从而使计算简便。
(3)先算括号里面的,再算括号外面的。
(4)利用加法交换律和结合律简算。
【详解】(1)
=
=
(2)
=
=
=
(3)
=
=
=
=
(4)
=
=
=2+1
=3
18.(1)6;10;9;(2)见详解;(答案不唯一)
【分析】(1)利用减法分别计算6-11岁之间测量硕硕的体重与同龄男孩标准体重之间的差值,比较6-11岁之间差值的大小,即可求出硕硕的体重在几岁时最接近标准体重以及在几岁时与标准体重相差最大。依次用硕硕7岁时体重减去6岁时的体重,8岁时体重减去7岁时的体重,9岁时体重减去8岁时的体重,10岁时体重减去9岁时的体重,11岁时体重减去10岁时的体重,求出当前岁数比上一年增长的体重,比较每一年增长体重的大小,即可求出在几岁时比上一年增长的幅度最大。
(2)观察统计图,实线数据整体高于虚线数据,表示硕硕的体重高于标准体重,建议合理即可。
【详解】(1)24-21=3(千克)
28-22=6(千克)
31-23=8(千克)
36-26=10(千克)
40-28=12(千克)
42-31=11(千克)
3<6<8<10<11<12
即硕硕的体重在6岁时最接近标准体重;在10岁时与标准体重相差最大。
28-24=4(千克)
31-28=3(千克)
36-31=5(千克)
40-36=4(千克)
42-40=2(千克)
2<3<4<5
即在9岁时比上一年增长的幅度最大。
(2)答:我给硕硕的建议是少吃高脂肪含量的食品,多多运动。(答案不唯一,合理即可)
【点睛】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
19.(1)折线;(2)出租车;(3)公交;出租;(4)
【分析】(1)以折线的上升或下降来表示统计数量的增减变化的统计图,叫作折线统计图。根据折线统计图的特征可知,这是一个折线统计图。
(2)观察折线统计图,折线的陡缓程度表示数据变化的快慢,虚线代表出租车的总数,实线代表公交车的总数,从陡缓程度来看,虚线明显更陡,说明出租车相比公交车,出租车的增长速度更快一些。
(3)2005年,出租车的总数是1万辆,公交车的总数是5万辆,2009年,出租车的总数是11万辆,公交车的总数是7万辆,比较大小即可得解。
(4)2013年,出租车的总数是50万辆,公交车的总数是15万辆,用出租车的总数除以公交车的总数,即可求出出租车的总数是公共汽车的几分之几。
【详解】(1)这是一个折线统计图。
(2)出租车增长的速度快一些。
(3)1<5,11>7
2005年,公交车总数多;2009年,出租车总数多。
(4)50÷15=
答:出租车的总数是公共汽车的。
【点睛】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
20.(1)见详解;
(2)11;12;
(3)矮
【分析】(1)根据表格中的数据在统计图中找出各对应点,依次连接各对应点,标准身高变化情况用虚线表示,小芳的身高变化情况用实线表示,最后在各点处标注数据;
(2)复式折线统计图中,折线向上走势越陡身高增长越快,折线走势越平缓身高增长越慢;
(3)代表小芳身高的折线在标准身高折线的下方时,小芳的身高比标准身高矮,代表小芳身高的折线在标准身高折线上方时,小芳的身高比标准身高高,据此解答。
【详解】(1)
(2)小芳从11岁到12岁身高增长得最快。
(3)分析可知,对比标准身高,小芳7~12岁身高在11岁之前偏矮。
【点睛】理解并掌握折线统计图的特点及作用,并且能够根据统计图提供的信息解决有关实际问题是解答题目的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.想要知道某市2024年5月份的气温变化情况,要搜集的数据是( )。
A.2024年各个季度平均气温 B.2024年各月平均气温
C.2024年5月每天的平均气温 D.2024年5月1日各时刻的气温
2.要比较凉山州2024年4月、5月的气温变化情况,绘制( )统计图更合理。
A.单式条形 B.复式条形 C.单式折线 D.复式折线
3.下面情形适合用折线统计图表示的是( )。
A.商场内空调、风扇、吹风机的销售情况
B.班级中喜欢吃香蕉、苹果、桔子、荔枝的人数
C.一天的气温变化情况
4.星期天,小红和妈妈从家出发步行到离家的公园,用时15分钟,在公园玩了半个小时,然后乘出租车回到家里,用时5分钟,下面图( )描述的是小红和妈妈的离家时间和离家距离的关系。
A. B. C.
5.下列说法中,正确的是( )。
A.把5米长的绳子分成8段,每段长米
B.因为18÷6=3,所以18是倍数,6和3是因数
C.两个质数的和一定是偶数
D.要表示出某商场去年每月销售量的变化情况,选用折线统计图比较合适
二、填空题
6.表示水位的升降变化的情况用( )统计图。
7.
(1)第( )周两种饮料的销售量最接近。
(2)第( )周两种饮料的销售量相差最大,相差( )。
(3)你建议超市老板后面一段时间将哪种饮料进多一些?为什么?
8.如图是某校两个篮球兴趣小组前五场比赛得分情况统计图,请根据统计图回答问题。
(1)两个小组第 场比赛的得分相差最少,两组成绩相差 分。
(2)两个小组第 场比赛的得分相差最多,两组成绩相差 分。
9.小华和小丽是一对龙凤双胞胎,每年在他们生日这天,妈妈都记录下他们各自的身高,如图。
(1)他们( )岁时,身高相同。
(2)同一年两人差距最大是( )厘米。
(3)小丽在11岁时身高超过了小华,之后小华在( )岁又反超了小丽。
10.下面是某位病人的体温记录折线统计图。
(1)根据上面的统计图把下面的统计表填写完整。
时间 2:00 5:00 8:00 11:00 14:00 17:00 20:00 23:00
体温/摄氏度 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
(2)护士每隔( ) 小时给病人量一次体温。
(3)图中的横虚线表示( )。
(4)从体温看,这个病人的病情( )。(填“好转”或“加重”)
三、判断题
11.折线统计图不仅便于直观了解数量的多少,还可以反映数量的增减变化。( )
12.如果要统计某地年至年每年新生婴儿不同性别人数变化情况,应制成复式折线统计图。( )
13.气象局要统计今年上半年每月的降水量变化情况,一般会绘制条形统计图。( )
14.要清楚地表示一个病人的体温变化情况,用折线统计图较好。( )
15.复式折线统计图是用图例区别事物的。( )
16.小明发烧了,妈妈想记录小明一天的体温,选用折线统计图记录较合适。( )
四、计算题
17.计算下面各题,能简算的要简算。
(1) (2) (3) (4)
五、解答题
18.硕硕每年生日时都测量体重,下面是他6-11岁之间测量的体重与同龄男孩标准体重对比的统计图。
(1)从图中可以看出,硕硕的体重在( )岁时最接近标准体重;在( )岁时与标准体重相差最大。在( )岁时比上一年增长的幅度最大。
(2)根据图中提供的信息,请你给硕硕提一些建议。
19.根据统计图完成下面各题。
(1)这是一个( )统计图。
(2)( )车增长的速度快一些。
(3)2005年,( )车总数多;2009年,( )车总数多。
(4)2013年,出租车的总数是公共汽车的几分之几?
20.下面是小芳7~12岁每年的身高与同龄女学生标准身高的对比统计表:
(1)根据表中的数据,画出折线统计图,并回答下面的问题。
(2)小芳从( )岁到( )岁身高增长得最快。
(3)对比标准身高,小芳7~12岁身高在11岁之前偏( )(填高或矮)。
《(基础篇)2024-2025学年下学期小学数学人教版五年级暑假分层作业第七单元《折线统计图》》参考答案
题号 1 2 3 4 5
答案 C D C A D
1.C
【分析】根据题意,要知道的是某市2024年5月份的气温变化情况,那么搜集的数据应该能够反映出这个月内气温的每日变化,而不是某个时间点或更长时间段的数据。
【详解】A.2024年各个季度平均气温,一年有4个季度,各个季度的数据范围太大了,无法具体看出5月份的气温变化情况,不符合题意;
B.2024年各月平均气温,一年有12个月,可以看出不同月份的平均气温,但不是5月份的气温变化情况,不符合题意;
C.2024年5月每天的平均气温,每天的数据能详细展示一个月内气温的变化情况,符合题意;
D.2024年5月1日各时刻的气温,只能看出这一天的气温变化,无法反映整个月的情况,不符合题意。
故答案为:C
2.D
【分析】单式条形统计图可以清楚地看出数量的多少。
复式条形统计图可以用不同的条形表示两种以上的量的多少。
单式折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况。
复式折线统计图通过两组以上数据的水平进行比较,可以容易地比较出两组以上数据的变化趋势,更清楚看出各类之间的比较。
【详解】要比较凉山州2024年4月、5月的气温变化情况,绘制复式折线统计图更合理。
故答案为:D
3.C
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;由此根据情况选择即可。
【详解】A.要统计商场内空调、风扇、吹风机的销售情况,用条形统计图较为合适;
B.要统计班级中喜欢吃香蕉、苹果、桔子、荔枝的人数,用条形统计图较为合适;
C.要统计一天的气温变化情况,用折线统计图较为合适。
故答案为:C
【点睛】此题应根据条形统计图、折线统计图各自的特点进行解答。
4.A
【分析】根据题意,小红和妈妈从家出发步行到离家的公园,用时15分钟,这时时间和离家距离都在增加;在公园玩了半个小时,时间又过去30分钟,但离家距离不变;然后乘出租车回到家里,用时5分钟,此时时间在增加,但离家距离不断减少,直至0m。据此逐项分析。
【详解】A。图中小红和妈妈从家出发步行到离家的公园,用时15分钟,之后在公园玩从15分钟到45分钟,玩了45-15=30(分钟),即半个小时,然后乘出租车回到家里,用时50-45=5(分钟),符合题意;
B.图中小红和妈妈从家出发步行到离家的公园,用时15分钟,然后直接乘出租车回到家里,用时20-15=5(分钟),不符合题意;
C.图中小红和妈妈从家出发步行到离家的公园,用时15分钟,之后在公园玩从15分钟到50分钟,玩了50-15=35(分钟),然后乘出租车回到家里,用时55-50=5(分钟),不符合题意。
故答案为:A
5.D
【分析】A.用绳子的长度除以平均分成的段数即可求出每段具体的长度;
B.在整数除法中,商是整数且没有余数,我们就说被除数是除数和商的倍数,除数和商是被除数的因数,因数和倍数是相互依存的,单独的一个数的不能说是因数或倍数;
C.一个自然数如果只有1和它本身两个因数,那么这个自然数叫做质数;是2的倍数的数叫做偶数;据此举例判断即可;
D.条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;据此判断即可。
【详解】A.把5米长的绳子分成8段,因为题干中并没有说明是平均分,所以不能求出每段的长度,原题干说法错误;
B.因为18÷6=3,所以18是6和3的因数,6和3是18的因数,原题干说法错误;
C.如:2和3都是质数,2+3=5,5是奇数,所以两个质数的和不一定是偶数,原题干说法错误;
D.要表示出某商场去年每月销售量的变化情况,选用折线统计图比较合适,说法正确。
故答案为:D
【点睛】本题考查因数和倍数,明确因数和倍数的定义是解题的关键。
6.折线
【分析】条形统计图可以清楚地看出数量的多少;
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况。
【详解】表示水位的升降变化的情况用折线统计图。
【点睛】理解掌握条形统计图、折线统计图的特点是选择统计图的关键。
7.(1)4
(2)2;34瓶
(3)老板多进一些乙种饮料,因为乙种饮料的销量逐渐上升。(答案不唯一,合理即可)
【分析】(1)黑色实线表示的是甲饮料的销售数量变化,黑色虚线表示的是乙饮料的销售数量变化,当两个变化曲线最接近的时候就是两种饮料销售数量最接近的时候,也就是第四周时候两种饮料销量最接近。
(2)黑色实线和黑色虚线距离最远的时候就是两种饮料相差最多时候,第二周甲销售84瓶,乙销售50瓶,所以相差34瓶。
(3)老板多进一些乙种饮料,因为乙种饮料的销量逐渐上升。(答案不唯一,合理即可)
【详解】(1)第4周两种饮料的销量最接近;
(2)第2周两种饮料的销售量相差最大,相差34瓶;
(3)老板多进一些乙种饮料,因为乙种饮料的销量逐渐上升。(答案不唯一,合理即可)
【点睛】主要考查折线统计图的相关知识,能够正确的认识折线统计图。
8.(1) 三 2
(2) 四 9
【分析】(1)观察折线统计图,实线代表第一小组的前五场比赛得分,虚线代表第二小组的前五场比赛得分,实线和虚线上点与点之间的位置相差最近的时候,即是两个小组比赛的得分相差最少的场次,找到此时对应的场次;并用这个场次中两个小组的得分相减即可;
(2)观察折线统计图,实线代表第一小组的前五场比赛得分,虚线代表第二小组的前五场比赛得分,实线和虚线上点与点之间的位置相差最远的时候,即是两个小组比赛的得分相差最多的场次,找到此时对应的场次;并用这个场次中两个小组的得分相减即可。
【详解】(1)两个小组第三场比赛的得分相差最少;
50-48=2(分)
即两组成绩相差2分。
(2)两个小组第四场比赛的得分相差最多;
54-45=9(分)
即两组成绩相差9分。
【点睛】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
9.(1)10
(2)2
(3)13
【分析】(1)折线统计图中横轴表示年龄,纵轴表示身高,实线表示小华的身高变化,虚线表示小丽的身高,两条线相交的地方就是身高相等,对应的横轴就是年龄,据此可得出答案。
(2)同一年年龄差距最大的,是两条虚线同一个横坐标上纵坐标的差距最大,据此得出答案。
(3)小华身高超过小丽的身高,即实线超过虚线的横坐标,据此得出答案。
【详解】(1)他们10岁时,身高相同。
(2)同一年两人差距最大是2厘米。
(3)小丽在11岁时身高超过了小华,之后小华在13岁又反超了小丽。
10.(1) 39.5 38 39 38 37.5 37 37.2 36.9
(2)3
(3)正常体温
(4)好转
【分析】(1)从折线统计图中读出各个时间点的体温,再填入统计表中即可。
(2)根据折线统计图的横轴可知,护士每隔3小时给病人量一次体温。
(3)折线统计图的横虚线是37℃,表示正常体温。
(4)根据折线统计图可知,这个病人的体温呈逐渐下降趋势,接近正常体温,说明病情好转。
【详解】(1)
时间 2:00 5:00 8:00 11:00 14:00 17:00 20:00 23:00
体温/摄氏度 39.5 38 39 38 37.5 37 37.2 36.9
(2)护士每隔3小时给病人量一次体温。
(3)图中的横虚线表示正常体温。
(4)从体温看,这个病人的病情好转。
【点睛】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
11.√
【详解】折线统计图不仅便于直观了解数量的多少,还可以反映数量的增减变化,说法正确。
故答案为:√
12.√
【分析】根据复式折线统计图的特征:可以同时显示多组数据,清晰的反映变化趋势,易于比较数据差异即可解答。
【详解】因为要统计某地年至年每年新生婴儿不同性别人数变化情况,所以适合用复式折线统计图反映其变化情况。
故答案为:√。
【点睛】本题考查了复式折线统计图的特征:可以同时显示多组数据,清晰的反映变化趋势,易于比较数据差异,熟记复式统计图的特征是解题的关键。
13.×
【分析】折线统计图用折线的起伏表示数据的增减变化情况。不仅可以表示数量的多少,而且可以反映数据的增减变化情况。条形统计图的特点是易于比较数据之间的差别,能清楚地表示出数量的多少。依此判断。
【详解】根据分析可知,气象局要统计今年上半年每月的降水量变化情况,一般会绘制折线统计图。
故答案为:×
【点睛】解答此题的关键是在于掌握折线统计图、条形统计图的特点。
14.√
【分析】条形统计图可以清楚地看出数量的多少;
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况。
【详解】要清楚地表示一个病人的体温变化情况,用折线统计图较好。
原题说法正确。
故答案为:√
【点睛】理解掌握条形统计图、折线统计图的特点是选择统计图的关键。
15.√
【分析】复式折线统计图表示2个及以上的量的增减变化情况,必须通过图例进行区别。
【详解】由分析可知:
复式折线统计图是用图例区别事物的。原题干说法正确。
故答案为:√
【点睛】本题考查了复式折线统计图,复式条形统计图也得通过图例进行区别。
16.√
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;由此根据情况选择即可。
【详解】由分析可得:小明发烧了,妈妈想记录小明一天的体温,选用折线统计图记录较合适,原题说法正确。
故答案为:√
17.(1);(2);(3);(4)3
【分析】(1)先通分把异分母的分数化成同分母的分数,再按照同分母分数加、减法的计算方法进行计算。
(2)先根据减法的性质去括号,再计算同分母分数的减法,从而使计算简便。
(3)先算括号里面的,再算括号外面的。
(4)利用加法交换律和结合律简算。
【详解】(1)
=
=
(2)
=
=
=
(3)
=
=
=
=
(4)
=
=
=2+1
=3
18.(1)6;10;9;(2)见详解;(答案不唯一)
【分析】(1)利用减法分别计算6-11岁之间测量硕硕的体重与同龄男孩标准体重之间的差值,比较6-11岁之间差值的大小,即可求出硕硕的体重在几岁时最接近标准体重以及在几岁时与标准体重相差最大。依次用硕硕7岁时体重减去6岁时的体重,8岁时体重减去7岁时的体重,9岁时体重减去8岁时的体重,10岁时体重减去9岁时的体重,11岁时体重减去10岁时的体重,求出当前岁数比上一年增长的体重,比较每一年增长体重的大小,即可求出在几岁时比上一年增长的幅度最大。
(2)观察统计图,实线数据整体高于虚线数据,表示硕硕的体重高于标准体重,建议合理即可。
【详解】(1)24-21=3(千克)
28-22=6(千克)
31-23=8(千克)
36-26=10(千克)
40-28=12(千克)
42-31=11(千克)
3<6<8<10<11<12
即硕硕的体重在6岁时最接近标准体重;在10岁时与标准体重相差最大。
28-24=4(千克)
31-28=3(千克)
36-31=5(千克)
40-36=4(千克)
42-40=2(千克)
2<3<4<5
即在9岁时比上一年增长的幅度最大。
(2)答:我给硕硕的建议是少吃高脂肪含量的食品,多多运动。(答案不唯一,合理即可)
【点睛】此题考查的目的是理解掌握复式折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
19.(1)折线;(2)出租车;(3)公交;出租;(4)
【分析】(1)以折线的上升或下降来表示统计数量的增减变化的统计图,叫作折线统计图。根据折线统计图的特征可知,这是一个折线统计图。
(2)观察折线统计图,折线的陡缓程度表示数据变化的快慢,虚线代表出租车的总数,实线代表公交车的总数,从陡缓程度来看,虚线明显更陡,说明出租车相比公交车,出租车的增长速度更快一些。
(3)2005年,出租车的总数是1万辆,公交车的总数是5万辆,2009年,出租车的总数是11万辆,公交车的总数是7万辆,比较大小即可得解。
(4)2013年,出租车的总数是50万辆,公交车的总数是15万辆,用出租车的总数除以公交车的总数,即可求出出租车的总数是公共汽车的几分之几。
【详解】(1)这是一个折线统计图。
(2)出租车增长的速度快一些。
(3)1<5,11>7
2005年,公交车总数多;2009年,出租车总数多。
(4)50÷15=
答:出租车的总数是公共汽车的。
【点睛】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
20.(1)见详解;
(2)11;12;
(3)矮
【分析】(1)根据表格中的数据在统计图中找出各对应点,依次连接各对应点,标准身高变化情况用虚线表示,小芳的身高变化情况用实线表示,最后在各点处标注数据;
(2)复式折线统计图中,折线向上走势越陡身高增长越快,折线走势越平缓身高增长越慢;
(3)代表小芳身高的折线在标准身高折线的下方时,小芳的身高比标准身高矮,代表小芳身高的折线在标准身高折线上方时,小芳的身高比标准身高高,据此解答。
【详解】(1)
(2)小芳从11岁到12岁身高增长得最快。
(3)分析可知,对比标准身高,小芳7~12岁身高在11岁之前偏矮。
【点睛】理解并掌握折线统计图的特点及作用,并且能够根据统计图提供的信息解决有关实际问题是解答题目的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
