苏科版新版数学七年级上册 平行线模型 课件(共33张PPT)
文档属性
| 名称 | 苏科版新版数学七年级上册 平行线模型 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 42.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-06 19:47:27 | ||
图片预览




文档简介
(共33张PPT)
第六章 平面图形的初步认识 6.4.5
平行线——
平行线模型
苏科版(2024)七年级上册数学课件
01
学习目标
03
课堂练习
02
新课讲解
04
课后总结
目录
学习目标
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
01 掌握3种基本的平行线模型,并熟练应用于角度计算
02 掌握2种升级版的平行线模型,并熟练应用于角度计算
学习目标
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
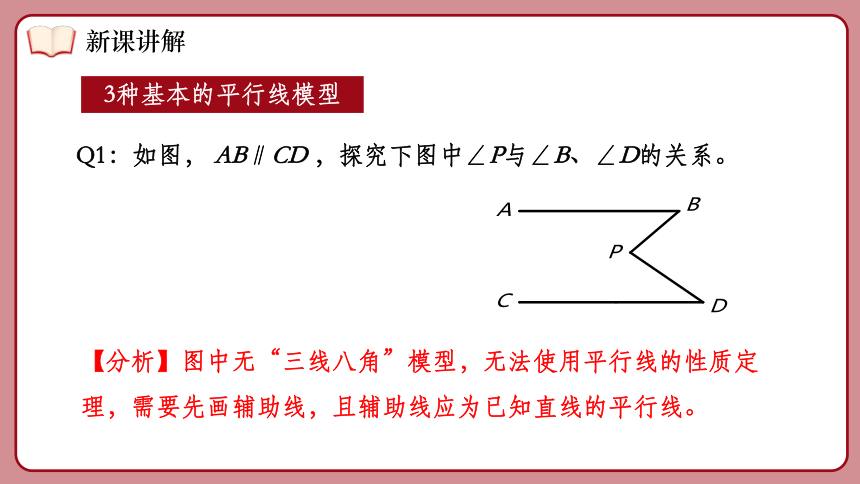
【分析】图中无“三线八角”模型,无法使用平行线的性质定理,需要先画辅助线,且辅助线应为已知直线的平行线。
Q1:如图, AB∥CD ,探究下图中∠P与∠B、∠D的关系。
新课讲解
3种基本的平行线模型
∵AB∥PQ,
∴∠B=∠1,
∵AB∥CD,∴CD∥PQ,
∴∠D=∠2,
又∵∠P=∠1+∠2,
∴∠P=∠B+∠D。
1
2
Q
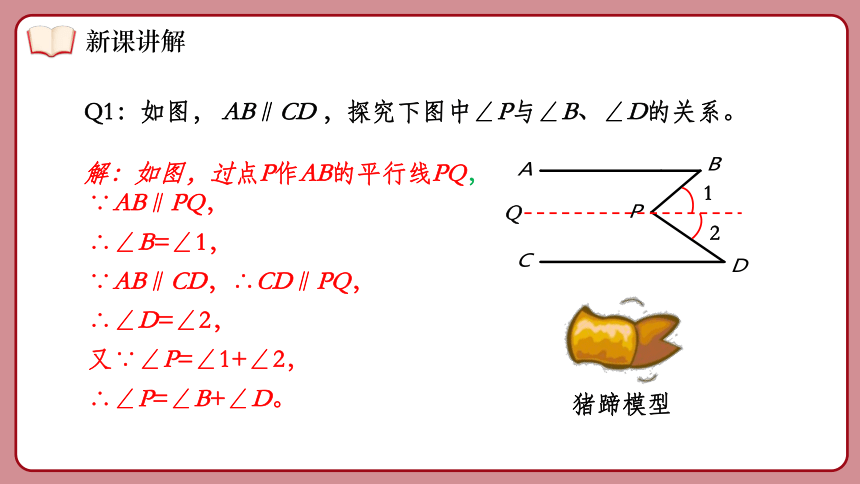
Q1:如图, AB∥CD ,探究下图中∠P与∠B、∠D的关系。
解:如图,过点P作AB的平行线PQ,
猪蹄模型
新课讲解
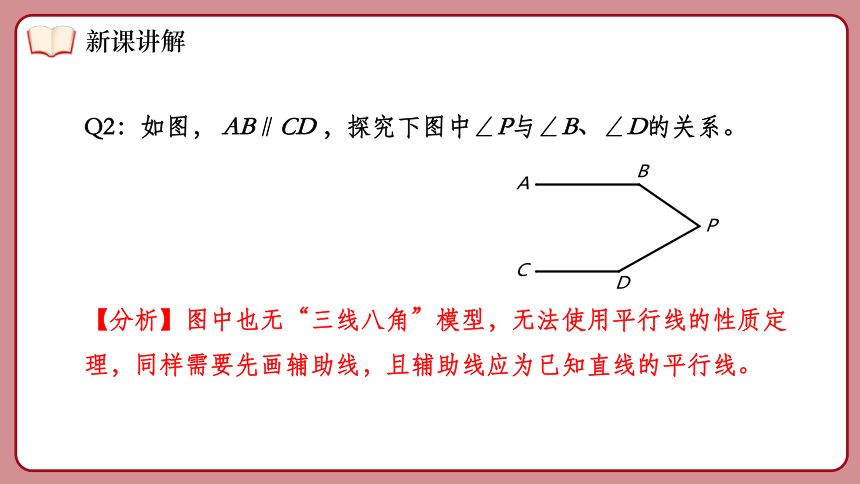
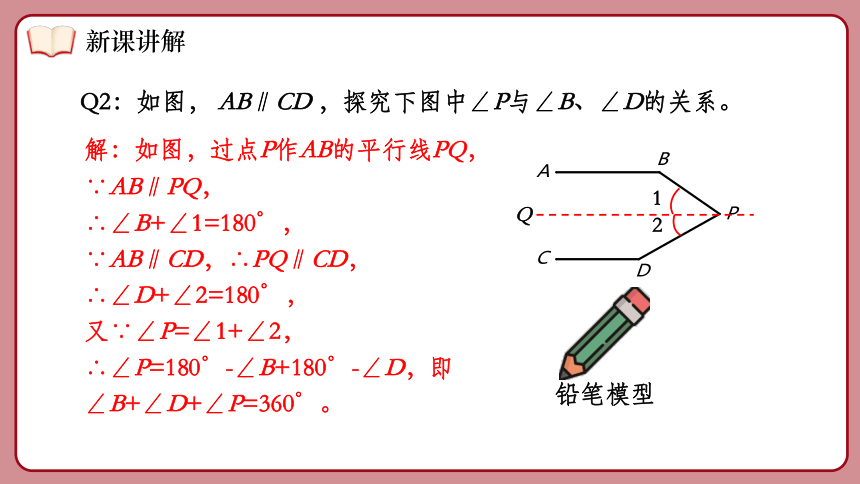
Q2:如图, AB∥CD ,探究下图中∠P与∠B、∠D的关系。
【分析】图中也无“三线八角”模型,无法使用平行线的性质定理,同样需要先画辅助线,且辅助线应为已知直线的平行线。
新课讲解
1
2
Q
Q2:如图, AB∥CD ,探究下图中∠P与∠B、∠D的关系。
∵AB∥PQ,
∴∠B+∠1=180°,
∵AB∥CD,∴PQ∥CD,
∴∠D+∠2=180°,
又∵∠P=∠1+∠2,
∴∠P=180°-∠B+180°-∠D,即∠B+∠D+∠P=360°。
解:如图,过点P作AB的平行线PQ,
铅笔模型
新课讲解
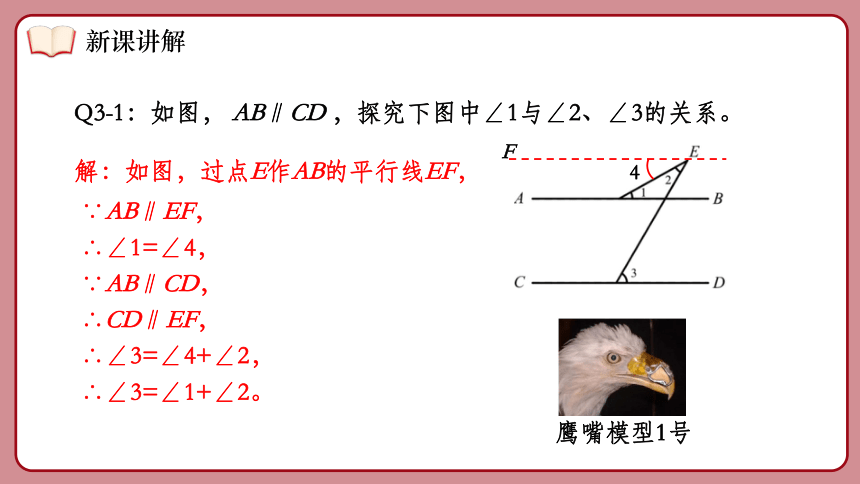
Q3-1:如图, AB∥CD ,探究下图中∠1与∠2、∠3的关系。
∵AB∥EF,
∴∠1=∠4,
∵AB∥CD,
∴CD∥EF,
∴∠3=∠4+∠2,
∴∠3=∠1+∠2。
解:如图,过点E作AB的平行线EF,
鹰嘴模型1号
F
4
新课讲解
4
F
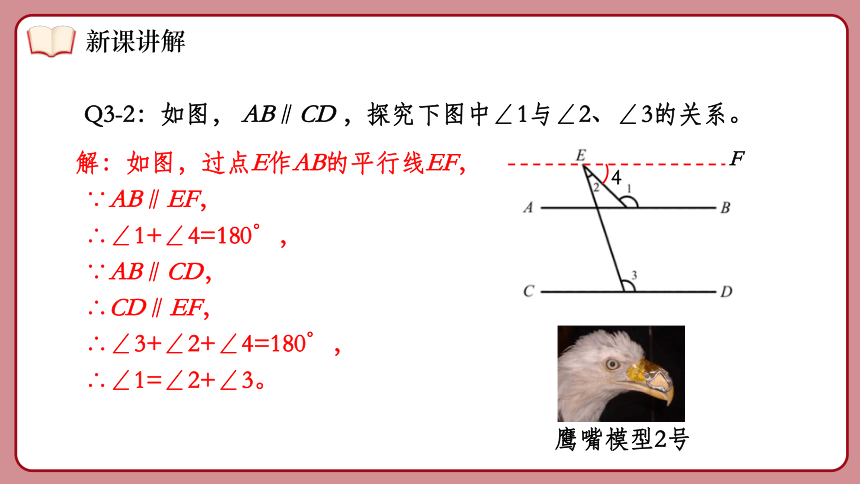
Q3-2:如图, AB∥CD ,探究下图中∠1与∠2、∠3的关系。
∵AB∥EF,
∴∠1+∠4=180°,
∵AB∥CD,
∴CD∥EF,
∴∠3+∠2+∠4=180°,
∴∠1=∠2+∠3。
解:如图,过点E作AB的平行线EF,
鹰嘴模型2号
新课讲解
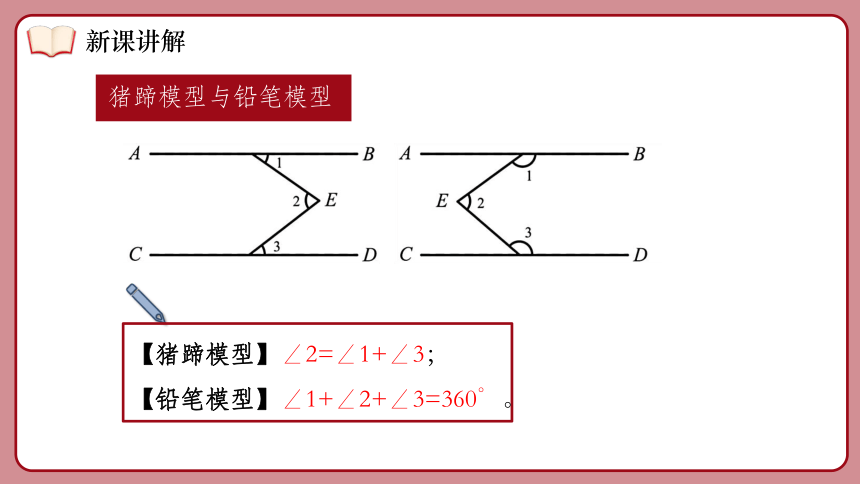
猪蹄模型与铅笔模型
【猪蹄模型】∠2=∠1+∠3;
【铅笔模型】∠1+∠2+∠3=360°。
新课讲解
2个鹰嘴模型
【2个鹰嘴模型】
左图:∠3=∠1+∠2;右图:∠1=∠2+∠3。
新课讲解
例1、如图,直线a∥b,∠P=75°,∠2=30°,则∠1=________。
【分析】
猪蹄模型:∠P=∠1+∠2
45°
例题讲解
例2、如图是中国机器人创意设计大赛中一参赛队员设计的机器人比赛时行走的路径;机器人从A点出发,到达B点,第一次拐的∠B是140°,第二次拐的∠C是100°,第三次拐的角是∠D,这时机器人行走的路径恰好和出发时行走的路径平行,那么∠D的度数是( )
A.100° B.120° C.140° D.90°
【分析】
子弹模型:∠B+∠C+∠D=360°
B
例题讲解
例3、如图,AB∥CD,∠C=75°,∠E=35°,则∠A为( )
A.90° B.35° C.40° D.75°
C
【分析】
鹰嘴模型:∠C=∠A+∠E
例题讲解
例4、如图,已知FD∥BE,则∠1-∠A+∠2等于( )
A.90° B.135° C.150° D.180°
D
【分析】
由鹰嘴模型可知:∠1=∠A+∠ABE,
∵∠ABE=180°-∠2,
∴∠1=∠A+180°-∠2,
即∠1-∠A+∠2=180°。
例题讲解
Q1-1:如图, AB∥CD ,探究下图中∠B、∠P、∠E、∠C之间的关系。
A
B
C
D
P
E
1
2
F
∵AB∥CD ,AB∥EF,
∴CD∥EF,∴∠C=∠2,
由猪蹄模型可知:∠P=∠B+∠1,
∴∠P+∠C=∠B+∠1+∠2,
即∠P+∠C=∠B+∠PEC。
锯齿模型-平行线之间2个拐点
解:如图,过点E作AB的平行线EF,
新课讲解
2种升级版本的平行线模型
Q1-2:如图, AB∥CD ,探究下图中∠B、∠P、∠E、∠Q、∠D之间的关系。
A
B
C
D
P
Q
E
2
1
F
由猪蹄模型可知:
∠P=∠B+∠1,∠Q=∠2+∠D,
∴∠P+∠Q=∠B+∠1+∠2+∠D,
即∠P+∠Q=∠B+∠PEQ+∠D。
解:如图,过点E作AB的平行线EF,
锯齿模型-平行线之间3个拐点
新课讲解
Q1-3:如图, AB∥CD ,探究下图中∠B、∠P、∠E、∠Q、∠M、∠C之间的关系。
1
2
F
由猪蹄模型可知:∠P=∠B+∠1,
由Q1-1中的锯齿模型可知:
∠Q+∠C=∠2+∠M,
∴∠P+∠Q+∠C=∠B+∠1+∠2+∠M,
即∠P+∠Q+∠C=∠B+∠PEQ+∠M。
解:如图,过点E作AB的平行线EF,
A
B
C
D
P
Q
E
M
锯齿模型-平行线之间4个拐点
新课讲解
Q1-4:通过以上三个锯齿模型图以及有关结论,你发现了什么?
A
B
C
D
P
E
A
B
C
D
P
Q
E
A
B
C
D
P
Q
E
M
∠P+∠Q+∠C=∠B+∠E+∠M
∠P+∠C=∠B+∠E
∠P+∠Q=∠B+∠E+∠D
锯齿模型是猪蹄模型的升级版,无论两平行线之间有几个拐点,其结论都为左角和=右角和。
新课讲解
Q2-1:如图, AB∥CD ,探究下图中∠B、∠P、∠Q、∠D之间的关系。
A
B
C
D
P
Q
1
2
F
∵CD∥QF,
∴∠2+∠D=180°,
由铅笔模型可知:∠B+∠P+∠1=360°,
∴∠B+∠P+∠1+∠2+∠D=540°,
即∠B+∠P+∠PQD+∠D=540°。
解:如图,过点Q作CD的平行线QF,
铅笔模型升级版
-平行线之间2个拐点
新课讲解
Q2-2:如图, AB∥CD ,探究下图中∠B、∠P、∠E、∠Q、∠D之间的关系。
1
2
F
由铅笔模型可知:
∠B+∠P+∠1=360°,
∠2+∠Q+∠D=360°,
∴∠B+∠P+∠1+∠2+∠Q+∠D=720°,
即∠B+∠P+∠PEQ+∠Q+∠D=720°。
解:如图,过点E作CD的平行线EF,
铅笔模型升级版
-平行线之间3个拐点
A
B
C
D
P
E
Q
新课讲解
Q2-3:如图, AB∥CD ,探究下图中∠B、∠P、∠E、∠F、∠Q、∠D之间的关系。
由铅笔模型可知:∠B+∠P+∠1=360°,
由Q2-1中的铅笔模型可知:
∠2+∠F+∠Q+∠D=540°,∴∠B+∠P+∠1+∠2+∠F+∠Q+∠D=900°,
即∠B+∠P+∠PEF+∠F+∠Q+∠D=900°。
解:如图,过点E作CD的平行线EM,
铅笔模型升级版
-平行线之间4个拐点
A
B
C
D
P
Q
E
F
1
2
M
新课讲解
Q2-3:通过以上三个铅笔模型图以及有关结论,你发现了什么?
∠B+∠P+∠E+∠F+∠Q+∠D=900°
铅笔模型升级版的结论与两平行线之间的拐点数有关,若拐点数为n,则结论为角度和=180°·(n+1)。
A
B
C
D
P
Q
2个拐点
A
B
C
D
P
E
Q
3个拐点
A
B
C
D
P
Q
E
F
4个拐点
∠B+∠P+∠E+∠Q+∠D=720°
∠B+∠P+∠Q+∠D=540°
新课讲解
锯齿模型
【锯齿模型】左角和=右角和。
新课讲解
铅笔模型升级版
【铅笔模型升级版】角度和=180°·(n+1)。
新课讲解
课堂练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
例1、如图,AB∥EF,∠C=90°,则α、β和γ的关系是( )
A.β=α+γ B.α+β+γ=180° C.α+β-γ=90° D.β+γ-α=180°
【分析】
锯齿模型:左角和=右角和
C
课堂练习
例2、从特殊到一般是数学研究的常用方法,有助于我们发现规律,探索问题的解。
(1)如图1,AB∥CD,点E为AB、CD之间的一点,∠1+∠MEN+∠2=_____°;
(2)如图2,AB∥CD,点E、F、G、H为AB、CD之间的四点,∠1+∠2+∠3+∠4+∠5+∠6=________°;
(3)如图3,AB∥CD,则∠1+∠2+∠3+…+∠n=________°。
【分析】铅笔模型升级版:
角度和=180°·(n+1)
360
900
180(n+1)
课堂练习
课后总结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
【猪蹄模型】∠2=∠1+∠3;
【铅笔模型】∠1+∠2+∠3=360°。
【2个鹰嘴模型】
左图:∠3=∠1+∠2;
右图:∠1=∠2+∠3。
【锯齿模型】左角和=右角和;
【铅笔模型升级版】角度和=180°·(n+1)。
课后总结
第六章 平面图形的初步认识 6.4.5
平行线——
平行线模型
苏科版(2024)七年级上册数学课件
第六章 平面图形的初步认识 6.4.5
平行线——
平行线模型
苏科版(2024)七年级上册数学课件
01
学习目标
03
课堂练习
02
新课讲解
04
课后总结
目录
学习目标
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
01 掌握3种基本的平行线模型,并熟练应用于角度计算
02 掌握2种升级版的平行线模型,并熟练应用于角度计算
学习目标
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
【分析】图中无“三线八角”模型,无法使用平行线的性质定理,需要先画辅助线,且辅助线应为已知直线的平行线。
Q1:如图, AB∥CD ,探究下图中∠P与∠B、∠D的关系。
新课讲解
3种基本的平行线模型
∵AB∥PQ,
∴∠B=∠1,
∵AB∥CD,∴CD∥PQ,
∴∠D=∠2,
又∵∠P=∠1+∠2,
∴∠P=∠B+∠D。
1
2
Q
Q1:如图, AB∥CD ,探究下图中∠P与∠B、∠D的关系。
解:如图,过点P作AB的平行线PQ,
猪蹄模型
新课讲解
Q2:如图, AB∥CD ,探究下图中∠P与∠B、∠D的关系。
【分析】图中也无“三线八角”模型,无法使用平行线的性质定理,同样需要先画辅助线,且辅助线应为已知直线的平行线。
新课讲解
1
2
Q
Q2:如图, AB∥CD ,探究下图中∠P与∠B、∠D的关系。
∵AB∥PQ,
∴∠B+∠1=180°,
∵AB∥CD,∴PQ∥CD,
∴∠D+∠2=180°,
又∵∠P=∠1+∠2,
∴∠P=180°-∠B+180°-∠D,即∠B+∠D+∠P=360°。
解:如图,过点P作AB的平行线PQ,
铅笔模型
新课讲解
Q3-1:如图, AB∥CD ,探究下图中∠1与∠2、∠3的关系。
∵AB∥EF,
∴∠1=∠4,
∵AB∥CD,
∴CD∥EF,
∴∠3=∠4+∠2,
∴∠3=∠1+∠2。
解:如图,过点E作AB的平行线EF,
鹰嘴模型1号
F
4
新课讲解
4
F
Q3-2:如图, AB∥CD ,探究下图中∠1与∠2、∠3的关系。
∵AB∥EF,
∴∠1+∠4=180°,
∵AB∥CD,
∴CD∥EF,
∴∠3+∠2+∠4=180°,
∴∠1=∠2+∠3。
解:如图,过点E作AB的平行线EF,
鹰嘴模型2号
新课讲解
猪蹄模型与铅笔模型
【猪蹄模型】∠2=∠1+∠3;
【铅笔模型】∠1+∠2+∠3=360°。
新课讲解
2个鹰嘴模型
【2个鹰嘴模型】
左图:∠3=∠1+∠2;右图:∠1=∠2+∠3。
新课讲解
例1、如图,直线a∥b,∠P=75°,∠2=30°,则∠1=________。
【分析】
猪蹄模型:∠P=∠1+∠2
45°
例题讲解
例2、如图是中国机器人创意设计大赛中一参赛队员设计的机器人比赛时行走的路径;机器人从A点出发,到达B点,第一次拐的∠B是140°,第二次拐的∠C是100°,第三次拐的角是∠D,这时机器人行走的路径恰好和出发时行走的路径平行,那么∠D的度数是( )
A.100° B.120° C.140° D.90°
【分析】
子弹模型:∠B+∠C+∠D=360°
B
例题讲解
例3、如图,AB∥CD,∠C=75°,∠E=35°,则∠A为( )
A.90° B.35° C.40° D.75°
C
【分析】
鹰嘴模型:∠C=∠A+∠E
例题讲解
例4、如图,已知FD∥BE,则∠1-∠A+∠2等于( )
A.90° B.135° C.150° D.180°
D
【分析】
由鹰嘴模型可知:∠1=∠A+∠ABE,
∵∠ABE=180°-∠2,
∴∠1=∠A+180°-∠2,
即∠1-∠A+∠2=180°。
例题讲解
Q1-1:如图, AB∥CD ,探究下图中∠B、∠P、∠E、∠C之间的关系。
A
B
C
D
P
E
1
2
F
∵AB∥CD ,AB∥EF,
∴CD∥EF,∴∠C=∠2,
由猪蹄模型可知:∠P=∠B+∠1,
∴∠P+∠C=∠B+∠1+∠2,
即∠P+∠C=∠B+∠PEC。
锯齿模型-平行线之间2个拐点
解:如图,过点E作AB的平行线EF,
新课讲解
2种升级版本的平行线模型
Q1-2:如图, AB∥CD ,探究下图中∠B、∠P、∠E、∠Q、∠D之间的关系。
A
B
C
D
P
Q
E
2
1
F
由猪蹄模型可知:
∠P=∠B+∠1,∠Q=∠2+∠D,
∴∠P+∠Q=∠B+∠1+∠2+∠D,
即∠P+∠Q=∠B+∠PEQ+∠D。
解:如图,过点E作AB的平行线EF,
锯齿模型-平行线之间3个拐点
新课讲解
Q1-3:如图, AB∥CD ,探究下图中∠B、∠P、∠E、∠Q、∠M、∠C之间的关系。
1
2
F
由猪蹄模型可知:∠P=∠B+∠1,
由Q1-1中的锯齿模型可知:
∠Q+∠C=∠2+∠M,
∴∠P+∠Q+∠C=∠B+∠1+∠2+∠M,
即∠P+∠Q+∠C=∠B+∠PEQ+∠M。
解:如图,过点E作AB的平行线EF,
A
B
C
D
P
Q
E
M
锯齿模型-平行线之间4个拐点
新课讲解
Q1-4:通过以上三个锯齿模型图以及有关结论,你发现了什么?
A
B
C
D
P
E
A
B
C
D
P
Q
E
A
B
C
D
P
Q
E
M
∠P+∠Q+∠C=∠B+∠E+∠M
∠P+∠C=∠B+∠E
∠P+∠Q=∠B+∠E+∠D
锯齿模型是猪蹄模型的升级版,无论两平行线之间有几个拐点,其结论都为左角和=右角和。
新课讲解
Q2-1:如图, AB∥CD ,探究下图中∠B、∠P、∠Q、∠D之间的关系。
A
B
C
D
P
Q
1
2
F
∵CD∥QF,
∴∠2+∠D=180°,
由铅笔模型可知:∠B+∠P+∠1=360°,
∴∠B+∠P+∠1+∠2+∠D=540°,
即∠B+∠P+∠PQD+∠D=540°。
解:如图,过点Q作CD的平行线QF,
铅笔模型升级版
-平行线之间2个拐点
新课讲解
Q2-2:如图, AB∥CD ,探究下图中∠B、∠P、∠E、∠Q、∠D之间的关系。
1
2
F
由铅笔模型可知:
∠B+∠P+∠1=360°,
∠2+∠Q+∠D=360°,
∴∠B+∠P+∠1+∠2+∠Q+∠D=720°,
即∠B+∠P+∠PEQ+∠Q+∠D=720°。
解:如图,过点E作CD的平行线EF,
铅笔模型升级版
-平行线之间3个拐点
A
B
C
D
P
E
Q
新课讲解
Q2-3:如图, AB∥CD ,探究下图中∠B、∠P、∠E、∠F、∠Q、∠D之间的关系。
由铅笔模型可知:∠B+∠P+∠1=360°,
由Q2-1中的铅笔模型可知:
∠2+∠F+∠Q+∠D=540°,∴∠B+∠P+∠1+∠2+∠F+∠Q+∠D=900°,
即∠B+∠P+∠PEF+∠F+∠Q+∠D=900°。
解:如图,过点E作CD的平行线EM,
铅笔模型升级版
-平行线之间4个拐点
A
B
C
D
P
Q
E
F
1
2
M
新课讲解
Q2-3:通过以上三个铅笔模型图以及有关结论,你发现了什么?
∠B+∠P+∠E+∠F+∠Q+∠D=900°
铅笔模型升级版的结论与两平行线之间的拐点数有关,若拐点数为n,则结论为角度和=180°·(n+1)。
A
B
C
D
P
Q
2个拐点
A
B
C
D
P
E
Q
3个拐点
A
B
C
D
P
Q
E
F
4个拐点
∠B+∠P+∠E+∠Q+∠D=720°
∠B+∠P+∠Q+∠D=540°
新课讲解
锯齿模型
【锯齿模型】左角和=右角和。
新课讲解
铅笔模型升级版
【铅笔模型升级版】角度和=180°·(n+1)。
新课讲解
课堂练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
例1、如图,AB∥EF,∠C=90°,则α、β和γ的关系是( )
A.β=α+γ B.α+β+γ=180° C.α+β-γ=90° D.β+γ-α=180°
【分析】
锯齿模型:左角和=右角和
C
课堂练习
例2、从特殊到一般是数学研究的常用方法,有助于我们发现规律,探索问题的解。
(1)如图1,AB∥CD,点E为AB、CD之间的一点,∠1+∠MEN+∠2=_____°;
(2)如图2,AB∥CD,点E、F、G、H为AB、CD之间的四点,∠1+∠2+∠3+∠4+∠5+∠6=________°;
(3)如图3,AB∥CD,则∠1+∠2+∠3+…+∠n=________°。
【分析】铅笔模型升级版:
角度和=180°·(n+1)
360
900
180(n+1)
课堂练习
课后总结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
【猪蹄模型】∠2=∠1+∠3;
【铅笔模型】∠1+∠2+∠3=360°。
【2个鹰嘴模型】
左图:∠3=∠1+∠2;
右图:∠1=∠2+∠3。
【锯齿模型】左角和=右角和;
【铅笔模型升级版】角度和=180°·(n+1)。
课后总结
第六章 平面图形的初步认识 6.4.5
平行线——
平行线模型
苏科版(2024)七年级上册数学课件
同课章节目录
