苏科版新版数学七年级上册 教学课件 6.2 角——补角、余角、角的大小比较(39张PPT)
文档属性
| 名称 | 苏科版新版数学七年级上册 教学课件 6.2 角——补角、余角、角的大小比较(39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 45.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-06 21:37:47 | ||
图片预览










文档简介
(共39张PPT)
第六章 平面图形的初步认识 6.2.2
角——
补角、余角、角的大小比较
苏科版(2024)七年级上册数学课件
01
学习目标
03
课堂练习
02
新课讲解
04
课后总结
目录
学习目标
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
学习目标
01 理解补角、余角的概念与性质
02 会用叠合的方法进行角的大小比较,
03 会用尺规作一个与已知角相等的角
04 理解角的平分线的概念,会用尺规作一个角的平分线
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
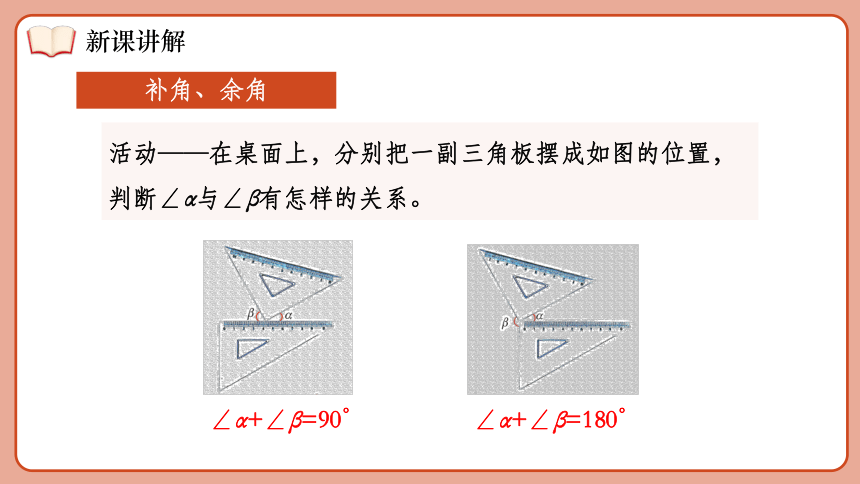
活动——在桌面上,分别把一副三角板摆成如图的位置,
判断∠α与∠β有怎样的关系。
∠α+∠β=90°
∠α+∠β=180°
新课讲解
补角、余角
补角的概念
如果两个角的度数之和等于180°,那么这两个角互为补角,简称互补。
eg:∠1=60°,∠2=120°,则∠1和∠2互为补角;
如图,∠α+∠β=180°,则∠α与∠β互补,∠α是∠β的补角,∠β是∠α的补角。
新课讲解
余角的概念
如果两个角的度数之和等于90°,那么这两个角互为余角,简称互余。
eg:∠3=20°,∠4=70°,则∠3和∠4互为余角;
如图,∠α+∠β=90°,则∠α与∠β互余,∠α是∠β的余角,∠β是∠α的余角。
新课讲解
练一练——1.填表:
∠α 50° n°(0∠α余角 45°
∠α的补角 120°
40°
130°
45°
135°
60°
30°
(90-n)°
(180-n)°
新课讲解
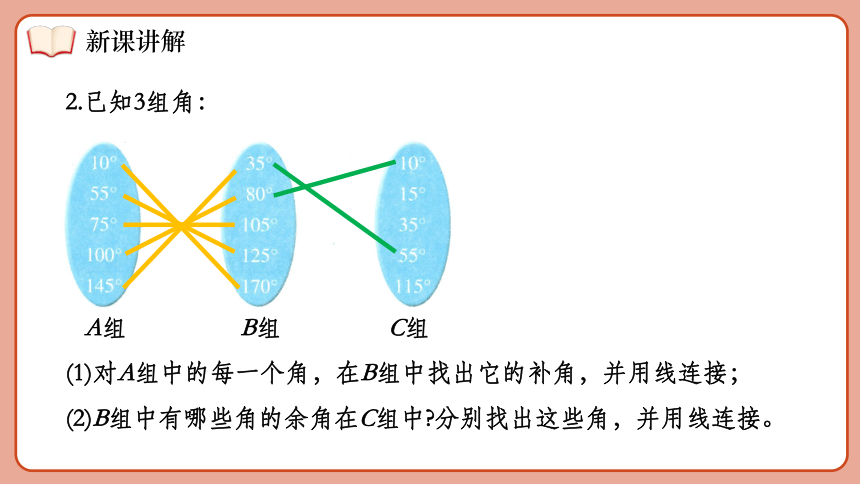
2.已知3组角:
A组 B组 C组
(1)对A组中的每一个角,在B组中找出它的补角,并用线连接;
(2)B组中有哪些角的余角在C组中 分别找出这些角,并用线连接。
新课讲解
问题——如果∠α与∠β互为补角,∠α与∠γ互为补角,
那么∠β与∠γ有怎样的数量关系
∵∠α与∠β互为补角,即∠α+∠β=180°,
∴∠β=180°-∠α,
同理,∠γ=180°-∠α,
∴∠β=∠γ。
新课讲解
补角、余角的性质
于是,我们得到如下结论:
你能证明出余角的性质吗?
同角(等角)的补角相等。
类似地,可以得到:
同角(等角)的余角相等。
新课讲解
如果∠α与∠β互为余角,∠α与∠γ互为余角,
证明:∠β=∠γ。
∵∠α与∠β互为余角,即∠α+∠β=90°,
∴∠β=90°-∠α,
同理,∠γ=90°-∠α,
∴∠β=∠γ。
新课讲解
例1、(1)若∠A=53°18',则∠A的补角的度数为( )
A.36°42' B.36°82' C.126°42' D.126°82'
【分析】由补角的定义可得:
∠A=180°-53°18′=126°42′。
C
例题讲解
例1、(2)若钝角∠1与∠2互补,∠2与∠3互余,则∠1与∠3的关系满足( )
A.∠1-∠3=90° B.∠1+∠3=90°
C.∠1+∠3=180° D.∠1=∠3
【分析】由补角、余角的定义可得:∠1+∠2=180°,∠2+∠3=90°,
∴∠2=180°-∠1,∠2=90°-∠3,
∴180°-∠1=90°-∠3,
∴∠1-∠3=90°。
A
例题讲解
例1、(3)若一个角的余角是它的补角的,则这个角的度数是( )
A.30° B.60° C.120° D.150°
【分析】设这个角为α,
则由补角、余角的定义可得:它的余角为90°-α,它的补角为180°-α,
∵一个角的余角是它的补角的,
∴90°-α=(180°-α),解得:α=30°。
A
例题讲解
例2、如图,若将三个含45°的直角三角板的直角顶点重合放置,若∠2=25°,∠3=35°,则∠1的度数为( )
A.25° B.30° C.35° D.40°
【分析】∵∠COD=∠AOB=90°,
∴∠4=∠2=25°(同角的余角相等),
∴∠1=∠EOF-∠2-∠3=90°-25°-35°=30°。
B
例题讲解
如果已知两个角的度数,那么可以通过度数来比较角的大小,
如果不知道两个角的度数,那么如何确定它们之间的大小关系呢
问题——下面两个钟面的大小相同,指针之间的夹角哪一个更大
新课讲解
角的大小比较、尺规作图、角的平分线
用叠合的方法比较大小。
O
B
A
O’
B’
A’
比较AB与A’B’的长短。
B’
A’
A
B
新课讲解
【法一】用叠合的方法比较大小的具体操作:
移动∠A’O’B’,使顶点O’与O重合,边O’B’与边OB重合,并使O’A’与OA在OB的同侧。
图1
O’
B’
A’
O
B
A
图2
O
B
A
O’
B’
A’
①若O’A’落在∠AOB的外部,则∠A’O’B’>∠AOB。
②若O’A’与OA重合,则∠A’O’B’=∠AOB。
③若O’A’落在∠AOB的内部,则∠A’O’B’<∠AOB。
叠合法比较角的大小
新课讲解
【法二】比较AB与A’B’的长短。
①若A’B’>AB,则∠A’O’B’>∠AOB。
②若A’B’=AB,则∠A’O’B’=∠AOB。
③若A’B’B’
A’
A
B
O
O’
新课讲解
角的大小比较
对于任意的∠α和∠β,下列三种关系中有且只有一种成立:
∠α<β,∠α=∠β,∠α>∠β。
新课讲解
如图,∠AOB可以看成是OB从OA出发,绕点O按逆时针方向旋转形成的,当点A,B之间的距离确定时,∠AOB的大小也随之确定。
利用上面的思路,我们可以用直尺和圆规作一个角等于已知角。
A
B
O
新课讲解
操作——尺规作图:如图,已知∠AOB,作∠A’O’B’,
使∠A’O’B’=∠AOB。
①以点O为圆心,任意长为半径作弧,分别交OA,OB于点C,D。
O
A
B
O
A
B
C
D
②作射线O’A’,以点O’为圆心,OC长为半径作弧PQ,交O’A’于点C’。
O’
A’
C’
P
Q
尺规作一个与已知角相等的角
新课讲解
③以点C’为圆心,CD长为半径作弧,交弧PQ于点D’。
④过点O’,D’作射线O’B’。
∠A’O’B’即为所求。
O’
A’
C’
D’
P
Q
O’
A’
B’
C’
D’
P
Q
尺规作一个与已知角相等的角
新课讲解
活动——在透明纸上画一个角,把这个角对折,使角的两边重合,再展开纸片,折痕把这个角分成的两个角相等吗
Yes
新课讲解
角的平分线
如果从角的顶点出发的一条射线把这个角分成两个相等的角,那么,这条射线叫作这个角的平分线。
如图,如果OC是∠AOB的平分线,
那么∠AOC=∠BOC=∠AOB或
∠AOB=2∠AOC=2∠BOC。
注意:角的平分线是一条射线。
新课讲解
操作——只用直尺和圆规,怎样作一个已知角(∠AOB)的平分线?
作法 图形
1.以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N;
2.分别以点M,N为圆心,大于MN的长为半径画弧在∠AOB的内部相交于点C; 3.画射线OC。射线OC即为所求。
尺规作一个角的平分线
新课讲解
讨论——如图,射线OC从∠AOB的边OA出发,
绕点O向边OB旋转,∠1和∠2的大小关系发生了怎样的变化
O
A
C
B
1
2
【分析】∠1逐渐增大,∠2的逐渐减小。
如图,作∠AOB的角平分线OD,
D
当射线OC绕点O旋转至射线OD前,∠1<∠2;
当射线OC绕点O旋转至射线OD时,∠1=∠2;
当射线OC绕点O旋转过射线OD后,∠1>∠2。
新课讲解
例1、如图,小明在用量角器度量∠AOB的大小时,将边OB放在0刻度线上,但是顶点O放在中心点的右侧,此时边OA刚好过50°刻度线,则∠AOB________50°。(选填“<”,“=”或“>”)
【分析】
设中心点是点C,过点C作CD∥AO。
>
C
D
例题讲解
例2、如图,OC为∠AOB内的一条射线,下列条件中不能确定OC平分∠AOB的是( )
A.∠AOC=∠BOC
B.∠AOC+∠COB=∠AOB
C.∠AOB=2∠BOC
D.∠AOC=∠AOB
B
例题讲解
课堂练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
例3、(1)如图,OA方向是北偏西40°方向,OB平分∠AOC,则∠BOC的度数为( )
A.50° B.55° C.60° D.65°
D
【分析】
∵OA方向是北偏西40°方向,
∴∠AOC=40°+90°=130°,
∵OB平分∠AOC,
∴∠BOC=∠AOC=65°。
课堂练习
例3、(2)如图,点O在直线AE上,OC平分∠AOE,∠DOB是直角,若∠1=25°,那么∠AOB的度数是_________。
25°
【分析】
∵点O在直线AE上,∴∠AOE=180°,
∵OC平分∠AOE,∴∠AOC=∠AOE=90°,
∴∠AOB+∠BOC=90°,
∵∠DOB是直角,∴∠DOB=∠BOC+∠1=90°,
∴∠AOB=∠1=25°。
课堂练习
例3、(3)如图,∠AOB=120°,OC是∠AOB内部任意一条射线,OD、OE分别是∠AOC、∠BOC的角平分线,下列叙述正确的是( )
A.∠DOE的度数不能确定 B.∠AOD=∠EOC
C.∠AOD+∠BOE=60° D.∠BOE=2∠COD
C
【分析】∵OD、OE分别是∠AOC、∠BOC的平分线,
∴∠AOD=∠COD=∠AOC,∠BOE=∠COE=∠BOC,
∴∠AOD+∠BOE=∠DOE=(∠BOC+∠AOC)=∠AOB=60°。
课堂练习
例4、OC、OD是∠AOB内部任意两条射线,OM平分∠AOC,ON平分∠BOD,若∠MON=m°,∠COD=n°,则∠AOB=__________°(用含m、n的代数式表示)。
【分析】设∠AOM=α,∠BON=β,
∵OM平分∠AOC,ON平分∠BOD,
∴∠COM=∠AOM=α,∠DON=∠BON=β,
∴∠AOC=2∠AOM=2α,∠DOB=2∠DON=2β,
∵∠MON=∠COM+∠COD+∠DON,
∴α+n°+β=m°,即α+β=m°-n°,
∴∠AOB=∠AOC+∠COD+∠DOB=2α+n°+2β=2(α+β)+n°=2m°-n°。
(2m-n)
课堂练习
课后总结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
补角、余角的概念:
如果两个角的度数之和等于180°,那么这两个角互为补角,简称互补。
如果两个角的度数之和等于90°,那么这两个角互为余角,简称互余。
补角、余角的性质:同角(等角)的补角相等。同角(等角)的余角相等。
角的大小比较:对于任意的∠α和∠β,下列三种关系中有且只有一种成立:∠α<β,∠α=∠β,∠α>∠β。
角的平分线:如果从角的顶点出发的一条射线把这个角分成两个相等的角,那么,这条射线叫作这个角的平分线。
课后总结
第六章 平面图形的初步认识 6.2.2
角——
补角、余角、角的大小比较
苏科版(2024)七年级上册数学课件
第六章 平面图形的初步认识 6.2.2
角——
补角、余角、角的大小比较
苏科版(2024)七年级上册数学课件
01
学习目标
03
课堂练习
02
新课讲解
04
课后总结
目录
学习目标
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
学习目标
01 理解补角、余角的概念与性质
02 会用叠合的方法进行角的大小比较,
03 会用尺规作一个与已知角相等的角
04 理解角的平分线的概念,会用尺规作一个角的平分线
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
活动——在桌面上,分别把一副三角板摆成如图的位置,
判断∠α与∠β有怎样的关系。
∠α+∠β=90°
∠α+∠β=180°
新课讲解
补角、余角
补角的概念
如果两个角的度数之和等于180°,那么这两个角互为补角,简称互补。
eg:∠1=60°,∠2=120°,则∠1和∠2互为补角;
如图,∠α+∠β=180°,则∠α与∠β互补,∠α是∠β的补角,∠β是∠α的补角。
新课讲解
余角的概念
如果两个角的度数之和等于90°,那么这两个角互为余角,简称互余。
eg:∠3=20°,∠4=70°,则∠3和∠4互为余角;
如图,∠α+∠β=90°,则∠α与∠β互余,∠α是∠β的余角,∠β是∠α的余角。
新课讲解
练一练——1.填表:
∠α 50° n°(0
∠α的补角 120°
40°
130°
45°
135°
60°
30°
(90-n)°
(180-n)°
新课讲解
2.已知3组角:
A组 B组 C组
(1)对A组中的每一个角,在B组中找出它的补角,并用线连接;
(2)B组中有哪些角的余角在C组中 分别找出这些角,并用线连接。
新课讲解
问题——如果∠α与∠β互为补角,∠α与∠γ互为补角,
那么∠β与∠γ有怎样的数量关系
∵∠α与∠β互为补角,即∠α+∠β=180°,
∴∠β=180°-∠α,
同理,∠γ=180°-∠α,
∴∠β=∠γ。
新课讲解
补角、余角的性质
于是,我们得到如下结论:
你能证明出余角的性质吗?
同角(等角)的补角相等。
类似地,可以得到:
同角(等角)的余角相等。
新课讲解
如果∠α与∠β互为余角,∠α与∠γ互为余角,
证明:∠β=∠γ。
∵∠α与∠β互为余角,即∠α+∠β=90°,
∴∠β=90°-∠α,
同理,∠γ=90°-∠α,
∴∠β=∠γ。
新课讲解
例1、(1)若∠A=53°18',则∠A的补角的度数为( )
A.36°42' B.36°82' C.126°42' D.126°82'
【分析】由补角的定义可得:
∠A=180°-53°18′=126°42′。
C
例题讲解
例1、(2)若钝角∠1与∠2互补,∠2与∠3互余,则∠1与∠3的关系满足( )
A.∠1-∠3=90° B.∠1+∠3=90°
C.∠1+∠3=180° D.∠1=∠3
【分析】由补角、余角的定义可得:∠1+∠2=180°,∠2+∠3=90°,
∴∠2=180°-∠1,∠2=90°-∠3,
∴180°-∠1=90°-∠3,
∴∠1-∠3=90°。
A
例题讲解
例1、(3)若一个角的余角是它的补角的,则这个角的度数是( )
A.30° B.60° C.120° D.150°
【分析】设这个角为α,
则由补角、余角的定义可得:它的余角为90°-α,它的补角为180°-α,
∵一个角的余角是它的补角的,
∴90°-α=(180°-α),解得:α=30°。
A
例题讲解
例2、如图,若将三个含45°的直角三角板的直角顶点重合放置,若∠2=25°,∠3=35°,则∠1的度数为( )
A.25° B.30° C.35° D.40°
【分析】∵∠COD=∠AOB=90°,
∴∠4=∠2=25°(同角的余角相等),
∴∠1=∠EOF-∠2-∠3=90°-25°-35°=30°。
B
例题讲解
如果已知两个角的度数,那么可以通过度数来比较角的大小,
如果不知道两个角的度数,那么如何确定它们之间的大小关系呢
问题——下面两个钟面的大小相同,指针之间的夹角哪一个更大
新课讲解
角的大小比较、尺规作图、角的平分线
用叠合的方法比较大小。
O
B
A
O’
B’
A’
比较AB与A’B’的长短。
B’
A’
A
B
新课讲解
【法一】用叠合的方法比较大小的具体操作:
移动∠A’O’B’,使顶点O’与O重合,边O’B’与边OB重合,并使O’A’与OA在OB的同侧。
图1
O’
B’
A’
O
B
A
图2
O
B
A
O’
B’
A’
①若O’A’落在∠AOB的外部,则∠A’O’B’>∠AOB。
②若O’A’与OA重合,则∠A’O’B’=∠AOB。
③若O’A’落在∠AOB的内部,则∠A’O’B’<∠AOB。
叠合法比较角的大小
新课讲解
【法二】比较AB与A’B’的长短。
①若A’B’>AB,则∠A’O’B’>∠AOB。
②若A’B’=AB,则∠A’O’B’=∠AOB。
③若A’B’
A’
A
B
O
O’
新课讲解
角的大小比较
对于任意的∠α和∠β,下列三种关系中有且只有一种成立:
∠α<β,∠α=∠β,∠α>∠β。
新课讲解
如图,∠AOB可以看成是OB从OA出发,绕点O按逆时针方向旋转形成的,当点A,B之间的距离确定时,∠AOB的大小也随之确定。
利用上面的思路,我们可以用直尺和圆规作一个角等于已知角。
A
B
O
新课讲解
操作——尺规作图:如图,已知∠AOB,作∠A’O’B’,
使∠A’O’B’=∠AOB。
①以点O为圆心,任意长为半径作弧,分别交OA,OB于点C,D。
O
A
B
O
A
B
C
D
②作射线O’A’,以点O’为圆心,OC长为半径作弧PQ,交O’A’于点C’。
O’
A’
C’
P
Q
尺规作一个与已知角相等的角
新课讲解
③以点C’为圆心,CD长为半径作弧,交弧PQ于点D’。
④过点O’,D’作射线O’B’。
∠A’O’B’即为所求。
O’
A’
C’
D’
P
Q
O’
A’
B’
C’
D’
P
Q
尺规作一个与已知角相等的角
新课讲解
活动——在透明纸上画一个角,把这个角对折,使角的两边重合,再展开纸片,折痕把这个角分成的两个角相等吗
Yes
新课讲解
角的平分线
如果从角的顶点出发的一条射线把这个角分成两个相等的角,那么,这条射线叫作这个角的平分线。
如图,如果OC是∠AOB的平分线,
那么∠AOC=∠BOC=∠AOB或
∠AOB=2∠AOC=2∠BOC。
注意:角的平分线是一条射线。
新课讲解
操作——只用直尺和圆规,怎样作一个已知角(∠AOB)的平分线?
作法 图形
1.以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N;
2.分别以点M,N为圆心,大于MN的长为半径画弧在∠AOB的内部相交于点C; 3.画射线OC。射线OC即为所求。
尺规作一个角的平分线
新课讲解
讨论——如图,射线OC从∠AOB的边OA出发,
绕点O向边OB旋转,∠1和∠2的大小关系发生了怎样的变化
O
A
C
B
1
2
【分析】∠1逐渐增大,∠2的逐渐减小。
如图,作∠AOB的角平分线OD,
D
当射线OC绕点O旋转至射线OD前,∠1<∠2;
当射线OC绕点O旋转至射线OD时,∠1=∠2;
当射线OC绕点O旋转过射线OD后,∠1>∠2。
新课讲解
例1、如图,小明在用量角器度量∠AOB的大小时,将边OB放在0刻度线上,但是顶点O放在中心点的右侧,此时边OA刚好过50°刻度线,则∠AOB________50°。(选填“<”,“=”或“>”)
【分析】
设中心点是点C,过点C作CD∥AO。
>
C
D
例题讲解
例2、如图,OC为∠AOB内的一条射线,下列条件中不能确定OC平分∠AOB的是( )
A.∠AOC=∠BOC
B.∠AOC+∠COB=∠AOB
C.∠AOB=2∠BOC
D.∠AOC=∠AOB
B
例题讲解
课堂练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
例3、(1)如图,OA方向是北偏西40°方向,OB平分∠AOC,则∠BOC的度数为( )
A.50° B.55° C.60° D.65°
D
【分析】
∵OA方向是北偏西40°方向,
∴∠AOC=40°+90°=130°,
∵OB平分∠AOC,
∴∠BOC=∠AOC=65°。
课堂练习
例3、(2)如图,点O在直线AE上,OC平分∠AOE,∠DOB是直角,若∠1=25°,那么∠AOB的度数是_________。
25°
【分析】
∵点O在直线AE上,∴∠AOE=180°,
∵OC平分∠AOE,∴∠AOC=∠AOE=90°,
∴∠AOB+∠BOC=90°,
∵∠DOB是直角,∴∠DOB=∠BOC+∠1=90°,
∴∠AOB=∠1=25°。
课堂练习
例3、(3)如图,∠AOB=120°,OC是∠AOB内部任意一条射线,OD、OE分别是∠AOC、∠BOC的角平分线,下列叙述正确的是( )
A.∠DOE的度数不能确定 B.∠AOD=∠EOC
C.∠AOD+∠BOE=60° D.∠BOE=2∠COD
C
【分析】∵OD、OE分别是∠AOC、∠BOC的平分线,
∴∠AOD=∠COD=∠AOC,∠BOE=∠COE=∠BOC,
∴∠AOD+∠BOE=∠DOE=(∠BOC+∠AOC)=∠AOB=60°。
课堂练习
例4、OC、OD是∠AOB内部任意两条射线,OM平分∠AOC,ON平分∠BOD,若∠MON=m°,∠COD=n°,则∠AOB=__________°(用含m、n的代数式表示)。
【分析】设∠AOM=α,∠BON=β,
∵OM平分∠AOC,ON平分∠BOD,
∴∠COM=∠AOM=α,∠DON=∠BON=β,
∴∠AOC=2∠AOM=2α,∠DOB=2∠DON=2β,
∵∠MON=∠COM+∠COD+∠DON,
∴α+n°+β=m°,即α+β=m°-n°,
∴∠AOB=∠AOC+∠COD+∠DOB=2α+n°+2β=2(α+β)+n°=2m°-n°。
(2m-n)
课堂练习
课后总结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
补角、余角的概念:
如果两个角的度数之和等于180°,那么这两个角互为补角,简称互补。
如果两个角的度数之和等于90°,那么这两个角互为余角,简称互余。
补角、余角的性质:同角(等角)的补角相等。同角(等角)的余角相等。
角的大小比较:对于任意的∠α和∠β,下列三种关系中有且只有一种成立:∠α<β,∠α=∠β,∠α>∠β。
角的平分线:如果从角的顶点出发的一条射线把这个角分成两个相等的角,那么,这条射线叫作这个角的平分线。
课后总结
第六章 平面图形的初步认识 6.2.2
角——
补角、余角、角的大小比较
苏科版(2024)七年级上册数学课件
同课章节目录
