苏科版新版数学七年级上册 教学课件 6.4 平行线——平行线的判定(二)(30张PPT)
文档属性
| 名称 | 苏科版新版数学七年级上册 教学课件 6.4 平行线——平行线的判定(二)(30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 40.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 07:58:32 | ||
图片预览






文档简介
(共30张PPT)
第六章 平面图形的初步认识 6.4.3
平行线——平行线
的判定(二)
苏科版(2024)七年级上册数学课件
01
学习目标
03
课堂练习
02
新课讲解
04
课后总结
目录
学习目标
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
01 借助于“三线八角”理解同旁内角的概念
02 掌握平行线的判定定理以及判定平行的其他方法,并将其熟练地应用于平行线的判定与证明当中去
学习目标
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
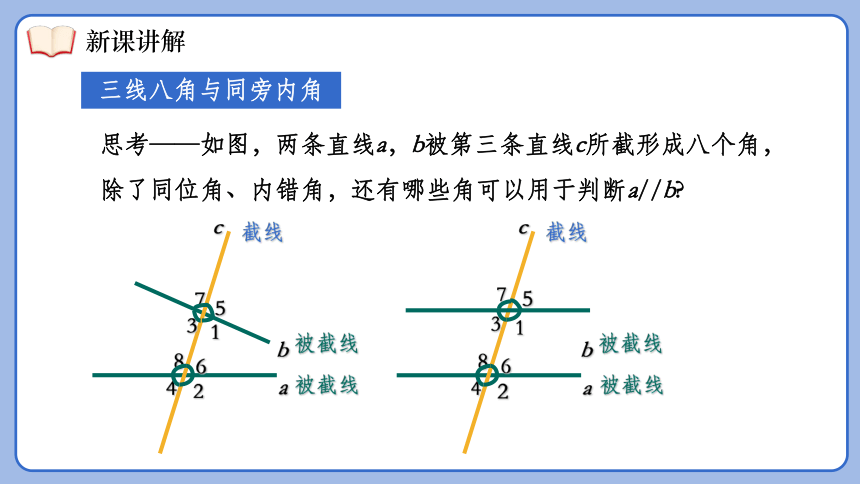
思考——如图,两条直线a,b被第三条直线c所截形成八个角,
除了同位角、内错角,还有哪些角可以用于判断a//b
b
a
c
被截线
被截线
截线
1
5
7
3
8
4
6
2
b
a
c
被截线
被截线
截线
1
5
7
3
8
4
6
2
新课讲解
三线八角与同旁内角
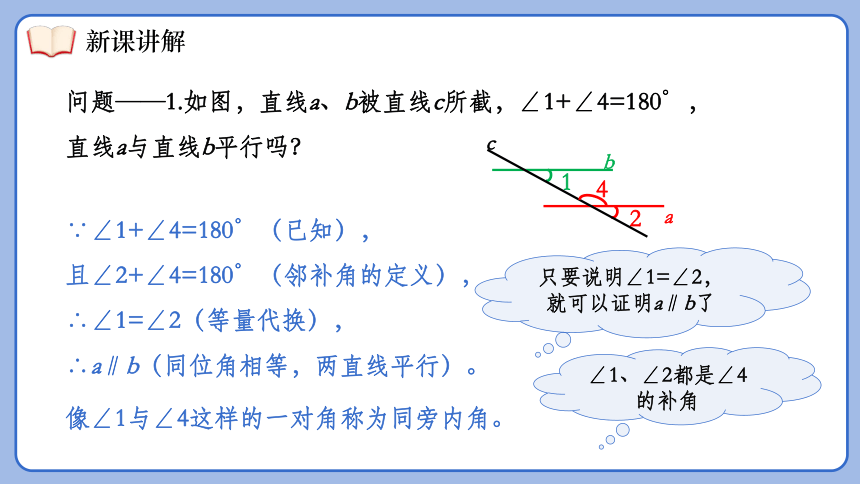
问题——1.如图,直线a、b被直线c所截,∠1+∠4=180°,
直线a与直线b平行吗?
只要说明∠1=∠2,就可以证明a∥b了
∠1、∠2都是∠4的补角
像∠1与∠4这样的一对角称为同旁内角。
a
b
2
1
c
4
∵∠1+∠4=180°(已知),
且∠2+∠4=180°(邻补角的定义),
∴∠1=∠2(等量代换),
∴a∥b(同位角相等,两直线平行)。
新课讲解
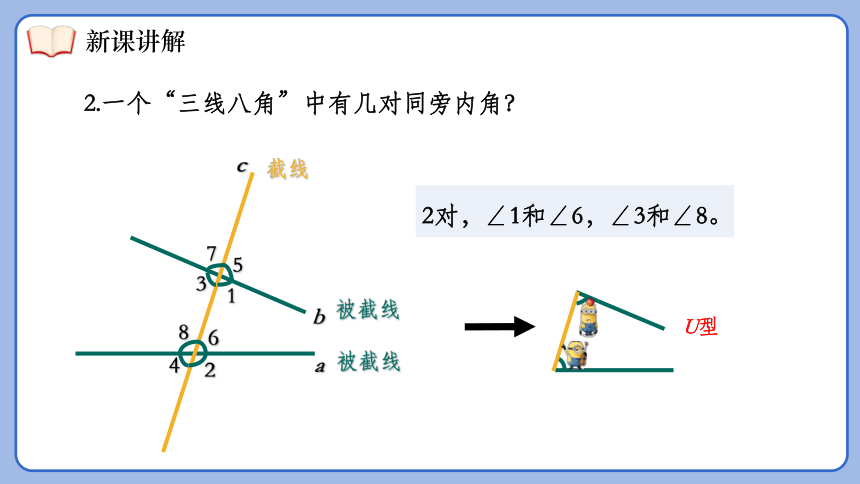
2.一个“三线八角”中有几对同旁内角?
2对,∠1和∠6,∠3和∠8。
b
a
c
被截线
被截线
截线
1
5
7
3
8
4
6
2
U型
新课讲解
3.同旁内角与被截线、截线之间有何位置关系?
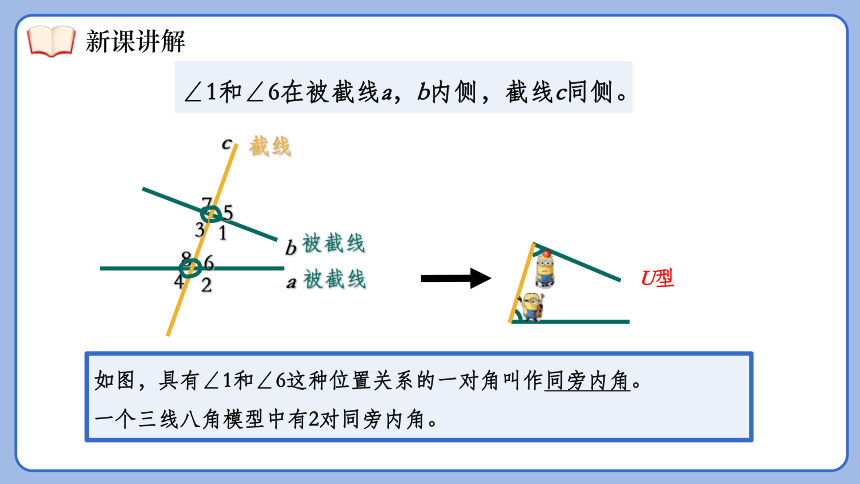
同旁内角在被截线内侧,截线同侧。
U型
新课讲解
如图,具有∠1和∠6这种位置关系的一对角叫作同旁内角。
一个三线八角模型中有2对同旁内角。
b
a
c
被截线
被截线
截线
1
5
7
3
8
4
6
2
∠1和∠6在被截线a,b内侧,截线c同侧。
U型
新课讲解
从“同位角相等,两直线平行”这个基本事实出发,可以得到平行线的判定定理:
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。(简单说成:同旁内角互补,两直线平行。)
平行线的判定定理
a
b
1
c
4
【符号语言】
∵∠1+∠4=180°(已知),
∴a∥b(同旁内角互补,两直线平行)。
新课讲解
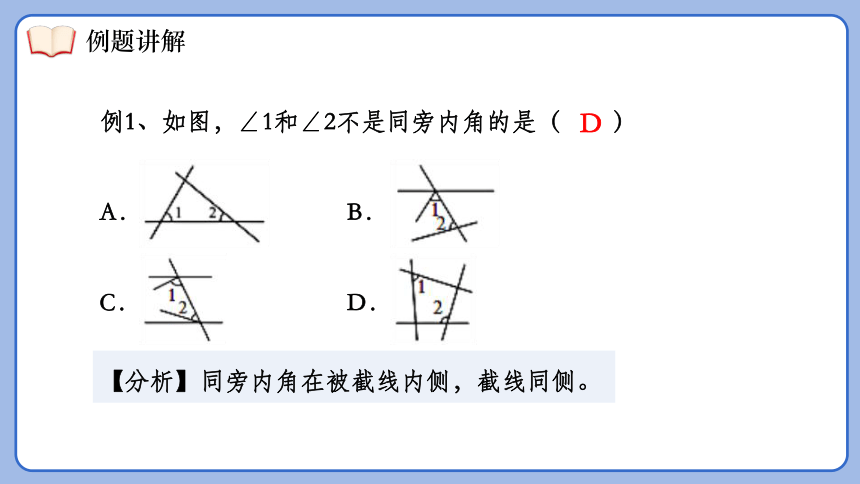
例1、如图,∠1和∠2不是同旁内角的是( )
A. B.
C. D.
D
【分析】同旁内角在被截线内侧,截线同侧。
例题讲解
例2、如图,直线AD、BE被直线BF和AC所截,下列说法正确的是( )
A.∠3与∠4是同旁内角
B.∠2与∠5是同位角
C.∠6与∠1是内错角
D.∠2与∠6是同旁内角
D
例题讲解
例3、若∠1与∠2是同旁内角,则( )
A.∠1与∠2不可能相等 B.∠1与∠2一定互补
C.∠1与∠2可能互余 D.∠1与∠2一定相等
C
【分析】
不要把“同旁内角”与“互补”画上等号!
例题讲解
例4、如图,直线EF交AB于G,交CD于M。
(1)图中有多少对同位角;
(2)图中有多少对内错角;
(3)图中有多少对同旁内角。
【分析1】如图,一个完整的三线八角模型,
有4对同位角,2对内错角,2对同旁内角。
例题讲解
例4、如图,直线EF交AB于G,交CD于M。
(1)图中有多少对同位角;
(2)图中有多少对内错角;
(3)图中有多少对同旁内角。
【分析2】如图,这个残缺的三线八角模型,
有2对同位角:∠EGH与∠EMD,∠DMF与∠HGF;
有1对内错角:∠CMG和∠HGM;
有1对同旁内角:∠DMG与∠HGM。
例题讲解
例4、如图,直线EF交AB于G,交CD于M。
(1)图中有多少对同位角;
(2)图中有多少对内错角;
(3)图中有多少对同旁内角。
【分析3】如图,这个残缺的三线八角模型,
有2对同位角:∠AGE与∠NME,∠NMF与∠AGF;
有1对内错角:∠NMG和∠BGM;
有1对同旁内角:∠AGM与∠NMG。
例题讲解
例4、如图,直线EF交AB于G,交CD于M。
(1)图中有多少对同位角;
(2)图中有多少对内错角;
(3)图中有多少对同旁内角。
【分析4】如图,这个残缺的三线八角模型,
有1对内错角:∠NMG和∠HGM。
综上,图中有8对同位角,图中有5对内错角,图中有4对同旁内角。
例题讲解
例5、如图,下列条件中,能判断AD∥BE的是( )
A.∠B=∠DCE
B.∠1=∠3
C.∠B+∠BCD=180°
D.∠B+∠BAD=180°
【分析】A.∠B=∠DCE→AB∥CD;
B.∠1=∠3→AB∥CD;
C.∠B+∠BCD=180°→AB∥CD;
D.∠B+∠BAD=180°→AD∥BE。
D
例题讲解
例6、已知:如图,BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90°,求证:AB∥CD。
证明:∵DE平分∠BDC(已知),
∴∠BDC=2∠1(角平分线的定义).
同理:∠ABD=2∠2(角平分线的定义),
∴∠BDC+∠ABD=2∠1+2∠2=2(∠1+∠2)(等式的性质),∵∠1+∠2=90°(已知),
∴∠ABD+∠BDC=180°(等量代换),
∴AB∥CD(同旁内角互补,两直线平行)。
例题讲解
探究——1.若a∥b,b∥c,则直线a与直线c有什么关系?
a∥c
b
a
c
【总结】平行于同一条直线的两直线平行。
新课讲解
判定平行的其他方法
2.若a⊥b,b⊥c,则直线a与直线c有什么关系?
b
a
c
若在同一平面内,则a∥c
b
c1
a
c2
若没有“在同一平面内”这一前提,则a∥c或a与c异面
【总结】在同一平面内,垂直于同一条直线的两直线平行。
新课讲解
1.平行的传递性:平行于同一条直线的两直线平行。
2.在同一平面内,垂直于同一条直线的两直线平行。
【符号语言】
若a∥b,b∥c,则a∥c。
在同一平面内,若a⊥b,b⊥c,则a∥c。
新课讲解
例1、下列命题中是真命题的是( )
A.同位角相等
B.平行于同一条直线的两直线平行
C.垂直于同一条直线的两直线平行
D.过一点作已知直线的平行线,有且只有一条
B
【分析】A、同位角不一定相等;
C、在同一平面内,垂直于同一条直线的两直线平行;
D、过直线外一点作已知直线的平行线,有且只有一条。
例题讲解
课堂练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
例2、画出的直线a与b不一定平行的是( )
A. B.
C. D.
A
【分析】 B.在同一平面内,垂直于同一条直线的两直线平行;
D.同位角相等,两直线平行。
课堂练习
例3、如图,∠BEC=∠B+∠C,求证:AB∥CD。
证明:如图,作∠FEB=∠B,
∵∠FEB=∠B(已知),
∴AB∥EF( 内错角相等,两直线平行),
又∵∠BEC=∠B+∠C=∠FEB+∠FEC(已知),
∴∠FEB+∠C=∠FEB+∠FEC,即∠C=∠FEC(等量代换),∴EF∥CD( 内错角相等,两直线平行),
∴AB∥CD(平行于同一条直线的两直线平行)。
F
课堂练习
课后总结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
三线八角与同位角、内错角:
如图,两条直线a、b被第三条直线c所截,形成8个角。
如图,具有∠1和∠6这种位置关系的一对角叫作同旁内角。一个三线八角模型中有2对同旁内角。
平行线的判定定理:同位角相等,两直线平行。内错角相等,两直线平行。同旁内角互补,两直线平行。
判定平行的其他方法:
1.平行的传递性:平行于同一条直线的两直线平行。
2.在同一平面内,垂直于同一条直线的两直线平行。
课后总结
第六章 平面图形的初步认识 6.4.3
平行线——平行线
的判定(二)
苏科版(2024)七年级上册数学课件
第六章 平面图形的初步认识 6.4.3
平行线——平行线
的判定(二)
苏科版(2024)七年级上册数学课件
01
学习目标
03
课堂练习
02
新课讲解
04
课后总结
目录
学习目标
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
01 借助于“三线八角”理解同旁内角的概念
02 掌握平行线的判定定理以及判定平行的其他方法,并将其熟练地应用于平行线的判定与证明当中去
学习目标
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
思考——如图,两条直线a,b被第三条直线c所截形成八个角,
除了同位角、内错角,还有哪些角可以用于判断a//b
b
a
c
被截线
被截线
截线
1
5
7
3
8
4
6
2
b
a
c
被截线
被截线
截线
1
5
7
3
8
4
6
2
新课讲解
三线八角与同旁内角
问题——1.如图,直线a、b被直线c所截,∠1+∠4=180°,
直线a与直线b平行吗?
只要说明∠1=∠2,就可以证明a∥b了
∠1、∠2都是∠4的补角
像∠1与∠4这样的一对角称为同旁内角。
a
b
2
1
c
4
∵∠1+∠4=180°(已知),
且∠2+∠4=180°(邻补角的定义),
∴∠1=∠2(等量代换),
∴a∥b(同位角相等,两直线平行)。
新课讲解
2.一个“三线八角”中有几对同旁内角?
2对,∠1和∠6,∠3和∠8。
b
a
c
被截线
被截线
截线
1
5
7
3
8
4
6
2
U型
新课讲解
3.同旁内角与被截线、截线之间有何位置关系?
同旁内角在被截线内侧,截线同侧。
U型
新课讲解
如图,具有∠1和∠6这种位置关系的一对角叫作同旁内角。
一个三线八角模型中有2对同旁内角。
b
a
c
被截线
被截线
截线
1
5
7
3
8
4
6
2
∠1和∠6在被截线a,b内侧,截线c同侧。
U型
新课讲解
从“同位角相等,两直线平行”这个基本事实出发,可以得到平行线的判定定理:
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。(简单说成:同旁内角互补,两直线平行。)
平行线的判定定理
a
b
1
c
4
【符号语言】
∵∠1+∠4=180°(已知),
∴a∥b(同旁内角互补,两直线平行)。
新课讲解
例1、如图,∠1和∠2不是同旁内角的是( )
A. B.
C. D.
D
【分析】同旁内角在被截线内侧,截线同侧。
例题讲解
例2、如图,直线AD、BE被直线BF和AC所截,下列说法正确的是( )
A.∠3与∠4是同旁内角
B.∠2与∠5是同位角
C.∠6与∠1是内错角
D.∠2与∠6是同旁内角
D
例题讲解
例3、若∠1与∠2是同旁内角,则( )
A.∠1与∠2不可能相等 B.∠1与∠2一定互补
C.∠1与∠2可能互余 D.∠1与∠2一定相等
C
【分析】
不要把“同旁内角”与“互补”画上等号!
例题讲解
例4、如图,直线EF交AB于G,交CD于M。
(1)图中有多少对同位角;
(2)图中有多少对内错角;
(3)图中有多少对同旁内角。
【分析1】如图,一个完整的三线八角模型,
有4对同位角,2对内错角,2对同旁内角。
例题讲解
例4、如图,直线EF交AB于G,交CD于M。
(1)图中有多少对同位角;
(2)图中有多少对内错角;
(3)图中有多少对同旁内角。
【分析2】如图,这个残缺的三线八角模型,
有2对同位角:∠EGH与∠EMD,∠DMF与∠HGF;
有1对内错角:∠CMG和∠HGM;
有1对同旁内角:∠DMG与∠HGM。
例题讲解
例4、如图,直线EF交AB于G,交CD于M。
(1)图中有多少对同位角;
(2)图中有多少对内错角;
(3)图中有多少对同旁内角。
【分析3】如图,这个残缺的三线八角模型,
有2对同位角:∠AGE与∠NME,∠NMF与∠AGF;
有1对内错角:∠NMG和∠BGM;
有1对同旁内角:∠AGM与∠NMG。
例题讲解
例4、如图,直线EF交AB于G,交CD于M。
(1)图中有多少对同位角;
(2)图中有多少对内错角;
(3)图中有多少对同旁内角。
【分析4】如图,这个残缺的三线八角模型,
有1对内错角:∠NMG和∠HGM。
综上,图中有8对同位角,图中有5对内错角,图中有4对同旁内角。
例题讲解
例5、如图,下列条件中,能判断AD∥BE的是( )
A.∠B=∠DCE
B.∠1=∠3
C.∠B+∠BCD=180°
D.∠B+∠BAD=180°
【分析】A.∠B=∠DCE→AB∥CD;
B.∠1=∠3→AB∥CD;
C.∠B+∠BCD=180°→AB∥CD;
D.∠B+∠BAD=180°→AD∥BE。
D
例题讲解
例6、已知:如图,BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90°,求证:AB∥CD。
证明:∵DE平分∠BDC(已知),
∴∠BDC=2∠1(角平分线的定义).
同理:∠ABD=2∠2(角平分线的定义),
∴∠BDC+∠ABD=2∠1+2∠2=2(∠1+∠2)(等式的性质),∵∠1+∠2=90°(已知),
∴∠ABD+∠BDC=180°(等量代换),
∴AB∥CD(同旁内角互补,两直线平行)。
例题讲解
探究——1.若a∥b,b∥c,则直线a与直线c有什么关系?
a∥c
b
a
c
【总结】平行于同一条直线的两直线平行。
新课讲解
判定平行的其他方法
2.若a⊥b,b⊥c,则直线a与直线c有什么关系?
b
a
c
若在同一平面内,则a∥c
b
c1
a
c2
若没有“在同一平面内”这一前提,则a∥c或a与c异面
【总结】在同一平面内,垂直于同一条直线的两直线平行。
新课讲解
1.平行的传递性:平行于同一条直线的两直线平行。
2.在同一平面内,垂直于同一条直线的两直线平行。
【符号语言】
若a∥b,b∥c,则a∥c。
在同一平面内,若a⊥b,b⊥c,则a∥c。
新课讲解
例1、下列命题中是真命题的是( )
A.同位角相等
B.平行于同一条直线的两直线平行
C.垂直于同一条直线的两直线平行
D.过一点作已知直线的平行线,有且只有一条
B
【分析】A、同位角不一定相等;
C、在同一平面内,垂直于同一条直线的两直线平行;
D、过直线外一点作已知直线的平行线,有且只有一条。
例题讲解
课堂练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
例2、画出的直线a与b不一定平行的是( )
A. B.
C. D.
A
【分析】 B.在同一平面内,垂直于同一条直线的两直线平行;
D.同位角相等,两直线平行。
课堂练习
例3、如图,∠BEC=∠B+∠C,求证:AB∥CD。
证明:如图,作∠FEB=∠B,
∵∠FEB=∠B(已知),
∴AB∥EF( 内错角相等,两直线平行),
又∵∠BEC=∠B+∠C=∠FEB+∠FEC(已知),
∴∠FEB+∠C=∠FEB+∠FEC,即∠C=∠FEC(等量代换),∴EF∥CD( 内错角相等,两直线平行),
∴AB∥CD(平行于同一条直线的两直线平行)。
F
课堂练习
课后总结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
三线八角与同位角、内错角:
如图,两条直线a、b被第三条直线c所截,形成8个角。
如图,具有∠1和∠6这种位置关系的一对角叫作同旁内角。一个三线八角模型中有2对同旁内角。
平行线的判定定理:同位角相等,两直线平行。内错角相等,两直线平行。同旁内角互补,两直线平行。
判定平行的其他方法:
1.平行的传递性:平行于同一条直线的两直线平行。
2.在同一平面内,垂直于同一条直线的两直线平行。
课后总结
第六章 平面图形的初步认识 6.4.3
平行线——平行线
的判定(二)
苏科版(2024)七年级上册数学课件
同课章节目录
