第五章 基本平面图形 综合测试题

第五章
基本平面图形
综合测试题
(45分钟
100分)
一、选择题(每小题4分,共28分)
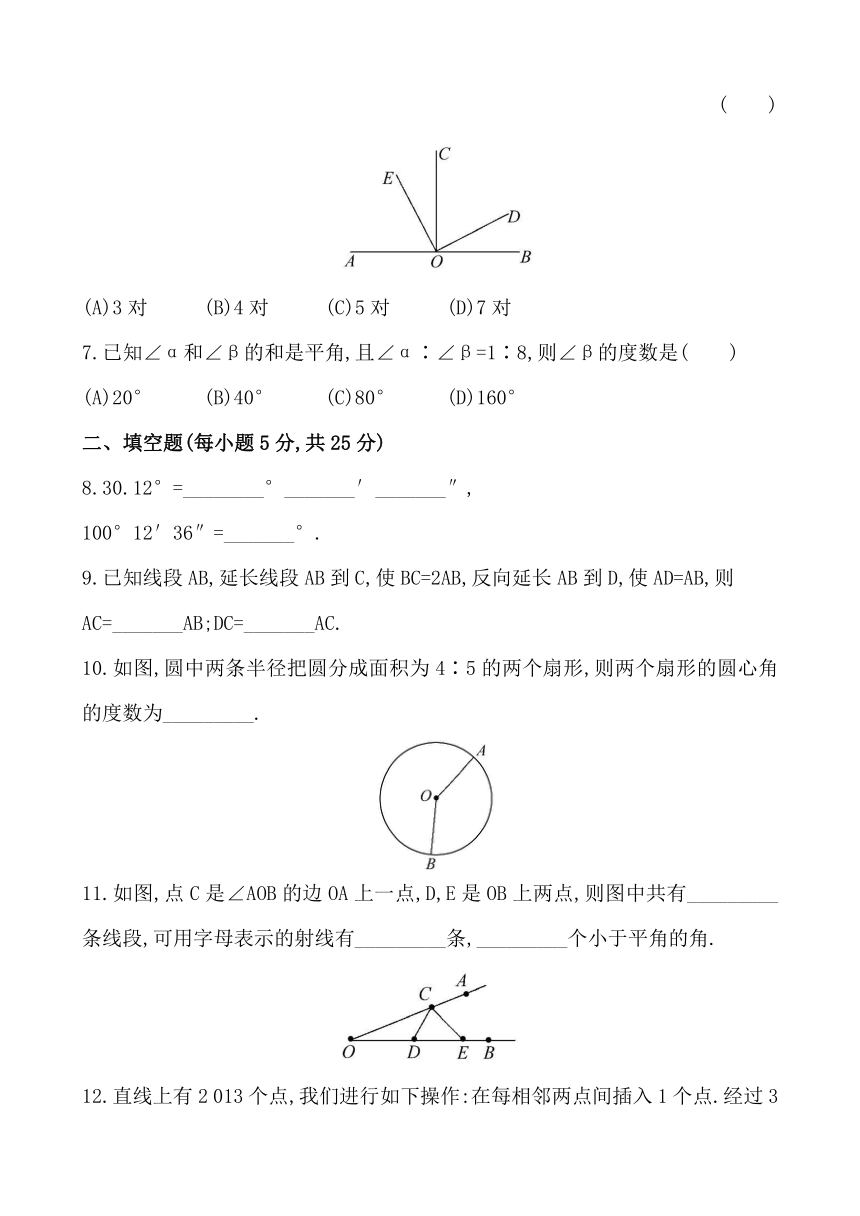
1.下列说法:①射线AB与射线BA是同一条射线;②线段AB是直线AB的一部分;③延长线段AB到C,使AB=AC;④射线AB与射线BA的公共部分是线段AB.正确的个数是(　　)
(A)1　　
(B)2　
　
(C)3　
　(D)4
2.如图所示,长度为12
cm的线段AB的中点为M,C为线段MB上一点,且MC∶CB=1∶2,则线段AC的长度为(　　)
(A)2
cm
(B)8
cm
(C)6
cm
(D)4
cm
3.下列说法正确的是(　　)
(A)角的两边可以度量
(B)一条直线可看成一个平角
(C)角是由一点引出的两条射线组成的图形
(D)一条射线可看成一个周角
4.如图,∠1=20°,∠AOC=90°,点B,O,D在同一条直线上,则∠2的度数为(　　)
(A)95°
(B)100°
(C)110°
(D)120°
5.如图,已知C是线段AB的中点,D是BC的中点,E是AD的中点,F是AE的中点,那么线段AF是线段AC的(　　)
(A)
(B)
QUOTE
(C)
(D)
6.如图,点O在直线AB上,∠COB=∠DOE=90°,那么图中相等的角的对数是
(　　)
(A)3对
(B)4对
(C)5对
(D)7对
7.已知∠α和∠β的和是平角,且∠α∶∠β=1∶8,则∠β的度数是(　　)
(A)20°
(B)40°
(C)80°
(D)160°
二、填空题(每小题5分,共25分)
8.30.12°=________°_______′_______″,
100°12′36″=_______°.
9.已知线段AB,延长线段AB到C,使BC=2AB,反向延长AB到D,使AD=AB,则
AC=_______AB;DC=_______AC.
10.如图,圆中两条半径把圆分成面积为4∶5的两个扇形,则两个扇形的圆心角的度数为_________.
11.如图,点C是∠AOB的边OA上一点,D,E是OB上两点,则图中共有_________条线段,可用字母表示的射线有_________条,_________个小于平角的角.
12.直线上有2
013个点,我们进行如下操作:在每相邻两点间插入1个点.经过3次这样的操作后,直线上共有_________个点.
三、解答题(共47分)
13.(11分)如图,已知C是AB的中点,D是AC的中点,E是BC的中点.
(1)若AB=18
cm,求DE的长;
(2)若CE=5
cm,求BD的长.
14.(11分)如图所示,∠AOB=30°,∠BOC=40°,∠COD=
26°,OE平分∠AOD.求∠BOE的度数.
15.(12分)如图所示,回答下列问题.
(1)2条直线相交有几个交点
(2)3条直线两两相交,最多有几个交点
(3)4条直线两两相交,最多有几个交点
(4)根据(1)(2)(3)总结:n(n为大于或等于2的正整数)条直线两两相交,最多有几个交点;
(5)根据上述结论,求100条直线两两相交最多有几个交点.
16.(13分)(1)如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;
(2)如果(1)中的∠AOB=α(OC在∠AOB外),其他条件不变,求∠MON的度数;
(3)如果(1)中的∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1)(2)(3)的结论中能得出什么结论
答案解析
1.【解析】选B.射线的端点不同,射线就不同,所以射线AB与射线BA不是同一条射线,①错;②对;③错,因为无法使AB=AC;④对;所以选B.
2.【解析】选B.因为AM=MB=AB=6(cm),MC=6×=2(cm),
所以AC=AM+MC=6+2=8(cm),故选B.
3.【解析】选C.角是由具有公共端点的两条射线组成的,可知C正确;射线不可以度量,故A错;角有顶点和两条边,故B,D错,因此选C.
4.【解析】选C.因为∠BOC=90°-20°=70°,
所以∠2=180°-∠BOC=180°-70°=110°.
5.【解析】选C.根据题意可设CD=DB=x,
则AC=CB=2DB=2x,AD=3x,AE=x,AF=AE=x,所以,故选C.
6.【解析】选C.因为∠COB=∠DOE=90°,
所以∠COE+∠COD=90°,∠COD+∠BOD=90°,
所以∠COE=∠BOD;因为∠AOC=∠DOE,所以∠COE+∠COD=90°,∠AOE+∠COE=
90°,所以∠AOE=∠COD;∠AOC=∠BOC.故选C.
7.【解析】选D.可设∠α=x,∠β=8x,
则x+8x=180°,x=20°,
所以∠β=8x=160°,故选D.
8.【解析】0.12°=0.12×60'=7.2',
0.2'=0.2×60″=12″,
所以30.12°=30°7'12″,
36″=36×()'=0.6',
12.6'=12.6×()°=0.21°,
所以100°12'36″=100.21°.
答案:30　
7
　
12　
100.21
9.【解析】如图所示,AC=3AB,DC=4AB,
所以DC=AC.
答案:3
10.【解析】两个扇形圆心角的度数分别为360°×=160°和360°×=200°.
答案:160°,200°
11.【解析】图中有线段OD,OE,OB,DE,DB,EB,OC,OA,CA,DC,EC,共11条,射线OA,CA,OB,DB,EB,共5条,小于平角的角有∠O,∠ODC,∠CDE,∠CED,∠CEB,∠ACE,∠ECD,∠DCO,∠ACD,∠OCE,共10个.
答案:11　
5　
10
12.【解析】2
013+2
012=4
025,4
025+4
024=8
049,8
049+8
048=16
097.
答案:16
097
13.【解析】(1)因为C是AB的中点,所以AC=BC=AB=9
cm.因为D是AC的中点,所以AD=DC=AC=
cm.因为E是BC的中点,所以CE=BE=BC=
cm.
又因为DE=DC+CE,所以DE=+=9(cm).
(2)由(1)知AD=DC=CE=BE,所以CE=BD.
因为CE=5
cm,所以BD=15
cm.
14.【解析】因为∠AOB=30°,∠BOC=40°,∠COD=26°,所以∠AOD=∠AOB+∠BOC+∠COD=30°+40°+26°=96°,
又因为OE平分∠AOD,
所以∠AOE=∠AOD=×96°=48°,
所以∠BOE=∠AOE-∠AOB=48°-30°=18°.
15.【解析】(1)由图可知,2条直线相交有1个交点.
(2)3条直线两两相交,最多有2+1=3个交点.
(3)4条直线两两相交,最多有3+2+1=6个交点.
(4)依此类推,n条直线两两相交最多有
n-1+…+3+2+1=个交点.
(5)根据上述结论,当n=100时,
==4
950个交点.
16.【解析】(1)因为ON是∠BOC的平分线,
所以∠CON=∠BON=∠BOC=×30°=15°.
因为OM是∠AOC的平分线,
所以∠COM=∠AOM=∠AOC
=(∠AOB+∠BOC)=
(90°+30°)=60°,
所以∠MON=∠COM-∠CON=60°-15°=45°.
(2)当∠AOB=α,其他条件不变时,
由(1)得∠CON=15°.因为OM是∠AOC的平分线,
所以∠COM=∠AOM=∠AOC=(∠AOB+∠BOC)=
(α+30°)=
α+15°,
所以∠MON=∠COM-∠CON=α+15°-15°
=α.
(3)当∠BOC=β,其他条件不变时,因为ON是∠BOC的平分线,所以∠CON=∠BON=
∠BOC=β,因为OM是∠AOC的平分线,所以∠COM=∠AOM=∠AOC=(∠AOB+
∠BOC)=
(90°+β)=45°+β,所以∠MON=∠COM-∠CON=45°+β-β=
45°.
(4)∠MON的度数总等于∠AOB的一半,而与锐角∠BOC的度数没有关系.