【期末押题卷】江苏省南京市2025-2026学年五年级上学期期末模拟数学预测卷苏教版(含解析)
文档属性
| 名称 | 【期末押题卷】江苏省南京市2025-2026学年五年级上学期期末模拟数学预测卷苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 22:22:30 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
江苏省南京市2025-2026学年五年级上学期期末模拟数学预测卷
一.计算题(共3小题,满分18分,每小题6分)
1.(6分)直接写得数。
2.5÷5= 75÷2.5= 6.2×2= 8÷3=
10.5÷0.5= 12÷11= 5.9﹣0.9= 6.06÷0.01=
2.(6分)计算下面各题,能简便的要用简便方法算。
(1)1.25×7.9×0.8 (2)63÷(1.7+1.9)+4.8
(3)8.4×13.5﹣3.5×8.4 (4)9.2÷0.25÷0.4
3.(6分)如图,在大正方形中,已知两个长方形的面积分别为15m2和40m2,求阴影正方形的面积。(请写出主要过程)
二.填空题(共8小题,满分16分,每小题2分)
4.(2分)体育老师对六年级女生进行了仰卧起坐的测验。每分钟19个为及格,记作0。小红的成绩记作+3,则她仰卧起坐的个数是 个。
5.(2分)亮亮今年12岁,比爸爸小m岁。5年后爸爸的年龄用含有字母的式子表示为 岁。
6.(2分)12支球队参加比赛,如果每2个球队之间进行一次比赛,至少要比赛 场。
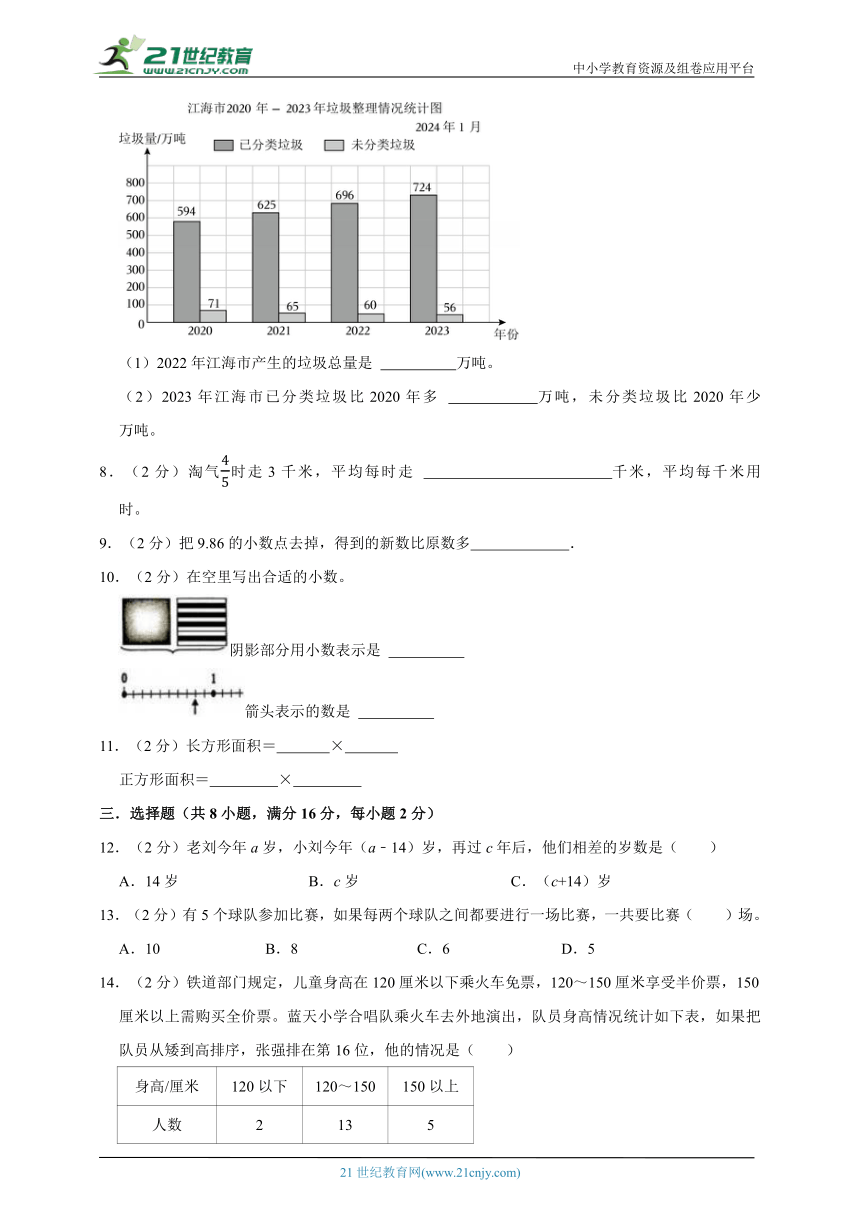
7.(2分)如图是江海市实行垃圾分类以来的垃圾整理情况统计图。
(1)2022年江海市产生的垃圾总量是 万吨。
(2)2023年江海市已分类垃圾比2020年多 万吨,未分类垃圾比2020年少 万吨。
8.(2分)淘气时走3千米,平均每时走 千米,平均每千米用 时。
9.(2分)把9.86的小数点去掉,得到的新数比原数多 .
10.(2分)在空里写出合适的小数。
阴影部分用小数表示是
箭头表示的数是
11.(2分)长方形面积= ×
正方形面积= ×
三.选择题(共8小题,满分16分,每小题2分)
12.(2分)老刘今年a岁,小刘今年(a﹣14)岁,再过c年后,他们相差的岁数是( )
A.14岁 B.c岁 C.(c+14)岁
13.(2分)有5个球队参加比赛,如果每两个球队之间都要进行一场比赛,一共要比赛( )场。
A.10 B.8 C.6 D.5
14.(2分)铁道部门规定,儿童身高在120厘米以下乘火车免票,120~150厘米享受半价票,150厘米以上需购买全价票。蓝天小学合唱队乘火车去外地演出,队员身高情况统计如下表,如果把队员从矮到高排序,张强排在第16位,他的情况是( )
身高/厘米 120以下 120~150 150以上
人数 2 13 5
A.免票 B.购买半价票
C.购买全价票
15.(2分)下列式子中,与2.6×1.2的积不相等的是( )
A.26×0.12 B.1.3×2.4 C.0.26×12 D.2.6×120
16.(2分)被减数有三位小数,减数有两位小数,差一定是( )位小数。
A.一 B.二 C.三 D.四
17.(2分)8.743中的“7”表示( )
A.7个十分之一 B.7个0.01
C.7个千分之一
18.(2分)淘气早上喝一袋牛奶容积是250( )
A.L B.mL C.立方分米
19.(2分)在﹣3,0,+5,﹣3,+3.1,,2003,+2008中负数有( )
A.2个 B.3个 C.4个
四.判断题(共4小题,满分8分,每小题2分)
20.(2分)一个长9分米、宽5分米的长方形纸板,最多能剪出11个边长是2分米的正方形。
21.(2分)(),利用了乘法的交换律和结合律。
22.(2分)通过割补法把一个平行四边形转化成一个长方形,这个长方形和平行四边形相比,周长和面积都不变。
23.(2分)某城市一天的最高气温为 9°C,最低气温为﹣2°C,该城市当天的温差为 7°C。
五.作图题(共1小题,满分6分,每小题6分)
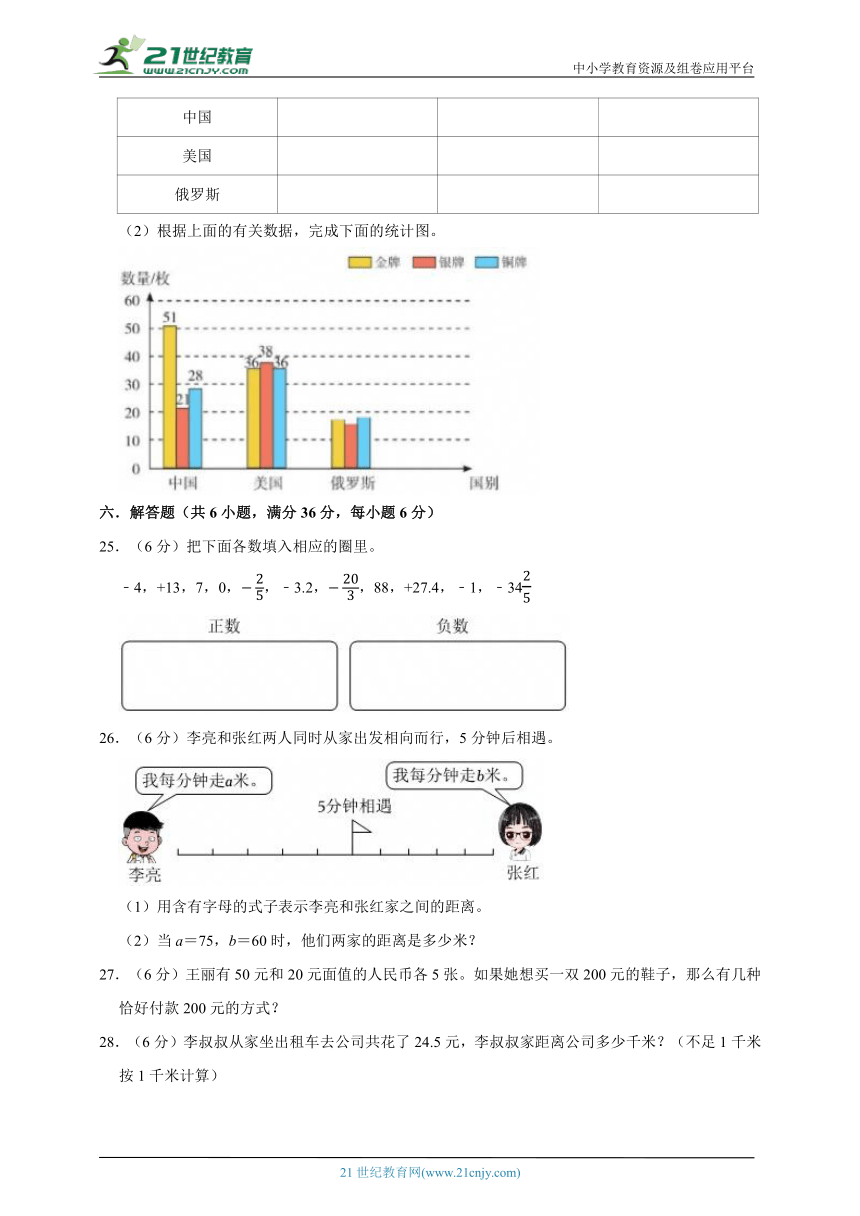
24.(6分)第29届奥林匹克运动会于8月8日在北京举行。赛后金牌数位居前三位的国家获三种奖牌情况如下:
中国 金牌51枚 银牌21枚 铜牌28枚
美国 金牌36枚 银牌38枚 铜牌36枚
俄罗斯 金牌23枚 银牌21枚 铜牌28枚
(1)根据以上资料,完成下面的统计表。
第29届奥运会金牌数位居前三位的国家获奖牌情况统计表
数量/枚 牌别 国别 金牌 银牌 铜牌
合计
中国
美国
俄罗斯
(2)根据上面的有关数据,完成下面的统计图。
六.解答题(共6小题,满分36分,每小题6分)
25.(6分)把下面各数填入相应的圈里。
﹣4,+13,7,0,,﹣3.2,,88,+27.4,﹣1,﹣34
26.(6分)李亮和张红两人同时从家出发相向而行,5分钟后相遇。
(1)用含有字母的式子表示李亮和张红家之间的距离。
(2)当a=75,b=60时,他们两家的距离是多少米?
27.(6分)王丽有50元和20元面值的人民币各5张。如果她想买一双200元的鞋子,那么有几种恰好付款200元的方式?
28.(6分)李叔叔从家坐出租车去公司共花了24.5元,李叔叔家距离公司多少千米?(不足1千米按1千米计算)
29.(6分)把一个边长是6分米的正方形铁丝框架拆开,用这些铁丝围成一个最大的等边三角形,这个等边三角形的边长是多少分米?
30.(6分)下图是某学校2019年春季达标运动会六年级(1)~(4)班体育达标情况统计图。
六年级(1)~(4)班体育达标情况统计图
请根据统计图中的信息完成上面的统计表,并回答下面的问题。
1.达标率最高的班级是( )达标率最低的班级是( )。
2.四个班的总人数是( )人,达标人数一共有( )人,估算总体达标率约为( )%。
参考答案与试题解析
计算题(共3小题,满分18分,每小题6分)
1.(6分)直接写得数。
2.5÷5= 75÷2.5= 6.2×2= 8÷3=
10.5÷0.5= 12÷11= 5.9﹣0.9= 6.06÷0.01=
【考点】小数除法;小数乘小数;小数乘法.
【专题】运算能力.
【答案】0.5;30;12.4;2.;21;1.;5;606。
【分析】根据小数减法、小数乘法、小数除法的运算法则直接写出得数即可。
【解答】解:
2.5÷5=0.5 75÷2.5=30 6.2×2=12.4 8÷3=2.
10.5÷0.5=21 12÷11=1. 5.9﹣0.9=5 6.06÷0.01=606
【点评】本题主要考查了小数减法、小数乘法、小数除法的运算,属于基本的计算,在平时注意积累经验,逐步提高运算的速度和准确性。
2.(6分)计算下面各题,能简便的要用简便方法算。
(1)1.25×7.9×0.8 (2)63÷(1.7+1.9)+4.8
(3)8.4×13.5﹣3.5×8.4 (4)9.2÷0.25÷0.4
【考点】小数乘法(推广整数乘法运算定律);小数四则混合运算;运算定律与简便运算.
【专题】数的运算;运算能力.
【答案】(1)7.9;
(2)22.3;
(3)84;
(4)92
【分析】(1)运用乘法的交换律、结合律进行简便计算。
(2)按照小数四则混合运算的顺序计算。
(3)运用乘法的分配律进行简便计算。
(4)根据除法的性质进行简算。
【解答】解:(1)1.25×7.9×0.8
=(1.25×0.8)×7.9
=1×7.9
=7.9
(2)63÷(1.7+1.9)+4.8
=63÷3.6+4.8
=17.5+4.8
=22.3
(3)8.4×13.5﹣3.5×8.4
=8.4×(13.5﹣3.5)
=8.4×10
=84
(4)9.2÷0.25÷0.4
=9.2÷(0.25×0.4)
=9.2÷0.1
=92
【点评】本题考查了运用运算定律进行简便计算和小数的四则混合运算。
3.(6分)如图,在大正方形中,已知两个长方形的面积分别为15m2和40m2,求阴影正方形的面积。(请写出主要过程)
【考点】组合图形的面积.
【专题】综合题;几何直观.
【答案】15的因数有1、3、5、15,40的因数有1、2、5、8、20、40,3×5=15,5×8=40,3+5=8(厘米),阴影正方形的边长是3厘米,3×3=9(平方厘米)。
【分析】依据题意结合图示可知,15的因数有1、3、5、15,40的因数有1、2、5、8、20、40,利用长方形的面积=长×宽,正方形的特点去解答。
【解答】解:15的因数有1、3、5、15,40的因数有1、2、5、8、20、40,3×5=15,5×8=40,3+5=8(厘米),阴影正方形的边长是3厘米,3×3=9(平方厘米)。
【点评】本题考查的是组合图形的面积的应用。
二.填空题(共8小题,满分16分,每小题2分)
4.(2分)体育老师对六年级女生进行了仰卧起坐的测验。每分钟19个为及格,记作0。小红的成绩记作+3,则她仰卧起坐的个数是 22 个。
【考点】负数的意义及其应用.
【答案】22。
【分析】用正负数表示意义相反的两种量:高于19分记作正,则低于19分就记作负。由此得解。
【解答】解:19+3=22(个)
答:小红的成绩记作+3,则她仰卧起坐的个数是22个。
故答案为:22。
【点评】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
5.(2分)亮亮今年12岁,比爸爸小m岁。5年后爸爸的年龄用含有字母的式子表示为 17+m 岁。
【考点】用字母表示数.
【专题】用字母表示数;应用意识.
【答案】17+m。
【分析】亮亮的年龄加上亮亮比爸爸小的年龄,求出爸爸今年的年龄,再用爸爸今年的年龄加上5,求出5年后爸爸的年龄。
【解答】解:12+m+5=17+m
答:5年后爸爸的年龄用含有字母的式子表示为(17+m)岁。
故答案为:17+m。
【点评】本题考查用字母表示数,明确数量间的关系是解题的关键。
6.(2分)12支球队参加比赛,如果每2个球队之间进行一次比赛,至少要比赛 66 场。
【考点】握手问题.
【专题】推理能力;应用意识.
【答案】66。
【分析】每两个队之间赛一场,那么每个队要赛11场,一共是(11×12)场,但是两队比赛是同一场比赛,所以(11×12)场比赛就多算了一倍,再除以2即可。
【解答】解:12×(12﹣1)÷2
=132÷2
=66(场)
答:至少要比赛66场。
故答案为:66。
【点评】本题属于握手问题,可利用握手问题的公式求解:握手次数=人数×(人数﹣1)÷2进行求解。
7.(2分)如图是江海市自2020年实行垃圾分类以来的垃圾整理情况统计图。
(1)2022年江海市产生的垃圾总量是 756 万吨。
(2)2023年江海市已分类垃圾比2020年多 130 万吨,未分类垃圾比2020年少 15 万吨。
【考点】以一当五(或以上)的条形统计图;从统计图表中获取信息.
【专题】综合填空题;应用意识.
【答案】(1)756;
(2)130,15。
【分析】(1)依据统计图用加法列式计算2022年江海市产生的垃圾总量;
(2)用减法列式计算2023年江海市已分类垃圾比2020年多多少万吨,用减法列式计算未分类垃圾比2020年少多少万吨。
【解答】解:(1)696+60=756(万吨)
答:2022年江海市产生的垃圾总量756万吨。
(2)724﹣594=130(万吨)
71﹣56=15(万吨)
答:2023年江海市已分类垃圾比2020年多130万吨,未分类垃圾比2020年少15万吨。
故答案为:(1)756;(2)130,15。
【点评】本题考查的是统计图的应用。
8.(2分)淘气时走3千米,平均每时走 千米,平均每千米用 时。
【考点】简单的行程问题.
【专题】应用题;数据分析观念.
【答案】,。
【分析】根据“淘气时走3千米”可根据“速度=路程÷时间”代入数值,求出淘气每小时走的路程,已知淘气走了1千米,可根据“时间=路程÷速度”对应数值求出平均每千米需要的时间,据此解答。
【解答】解:3(千米)
1(时)
答:平均每时走千米,平均每千米用时。
故答案为:,。
【点评】此题主要考查路程、速度、时间三者的关系式:路程=速度×时间,速度=路程÷时间,时间=路程÷速度,灵活变形列式解决问题。
9.(2分)把9.86的小数点去掉,得到的新数比原数多 976.14 .
【考点】小数的加法和减法.
【专题】文字叙述题.
【答案】见试题解答内容
【分析】9.86去掉小数点后是986,它比原数多多少,只要再减去原数即可.
【解答】解:986﹣9.86=976.14.
答:得到的新数比原数多976.14.
故答案为:976.14.
【点评】本题的重点是求出去掉小数点后的新数,再根据减法的意义解答.
10.(2分)在空里写出合适的小数。
阴影部分用小数表示是 1.4
箭头表示的数是 0.8
【考点】小数的读写、意义及分类.
【专题】数感.
【答案】1.4,0.8。
【分析】把整个图形看作单位“1”平均分成10份,每份表示0.1,则题中的阴影部分用小数表示为1.4;
把1平均分成10份,每份表示0.1,所以箭头表示的数是 0.8;由此解答即可。
【解答】解:阴影部分用小数表示是 1.4
箭头表示的数是 0.8
故答案为:1.4,0.8。
【点评】此题考查小数的意义和表示方法,明确每个单位长度表示多少,是解答此题的关键。
11.(2分)长方形面积= 长 × 宽
正方形面积= 边长 × 边长
【考点】长方形、正方形的面积.
【专题】应用意识.
【答案】长,宽,边长,边长。
【分析】根据长方形、正方形的面积公式解答即可。
【解答】解:长方形的面积=长×宽,正方形的面积=边长×边长。
故答案为:长,宽,边长,边长。
【点评】此题考查的目的是理解掌握长方形、正方形的面积公式及应用。
三.选择题(共8小题,满分16分,每小题2分)
12.(2分)老刘今年a岁,小刘今年(a﹣14)岁,再过c年后,他们相差的岁数是( )
A.14岁 B.c岁 C.(c+14)岁
【考点】年龄问题;用字母表示数.
【专题】综合填空题;设数法;年龄问题.
【答案】A
【分析】因为年龄差是一个不变的数值,所以老王和小李c年后的年龄差,也就是今年的年龄差.
【解答】解:a﹣(a﹣14)=14(岁)
现在相差14岁,c年后还是相差19岁.
答:再过c年后,他们相差的岁数是14岁.
故选:A.
【点评】此题考查年龄问题,要注意:两个人的年龄差是一个永远也不变的数值.
13.(2分)有5个球队参加比赛,如果每两个球队之间都要进行一场比赛,一共要比赛( )场。
A.10 B.8 C.6 D.5
【考点】排列组合;握手问题.
【专题】压轴题;应用意识.
【答案】A
【分析】如果每两个球队之间都要进行一场比赛,相当于两两组合,根据握手问题的公式n(n﹣1)÷2解答即可。
【解答】解:5×(5﹣1)÷2
=20÷2
=10(场)
答:一共要比赛10场。
故选:A。
【点评】本题考查了握手问题的实际应用,要注意去掉重复计算的情况,如果数量比较少可以用枚举法解答,如果数量比较多可以用公式n(n﹣1)÷2解答。
14.(2分)铁道部门规定,儿童身高在120厘米以下乘火车免票,120~150厘米享受半价票,150厘米以上需购买全价票。蓝天小学合唱队乘火车去外地演出,队员身高情况统计如下表,如果把队员从矮到高排序,张强排在第16位,他的情况是( )
身高/厘米 120以下 120~150 150以上
人数 2 13 5
A.免票 B.购买半价票
C.购买全价票
【考点】从统计图表中获取信息.
【专题】应用题;应用意识.
【答案】C
【分析】通过观察统计表可知,蓝天小学合唱队共有20人,其中120厘米以下的有2人,150厘米以上的5人,把合唱队员从矮到高排成一排,张强排在第16位,由此可知,张强的身高在150厘米以上,所以按规定张强应购买全价票。据此解答。
【解答】解:蓝天小学合唱队共有20人,其中120厘米以下的有2人,150厘米以上的5人,把合唱队员从矮到高排成一排,张强排在第16位,由此可知,张强的身高在150厘米以上,所以按规定张强应购买全价票。
故选:C。
【点评】本题考查的目的是理解掌握统计表的特点及作用,并且能够根据统计表提供的信息,解决有关的实际问题。
15.(2分)下列式子中,与2.6×1.2的积不相等的是( )
A.26×0.12 B.1.3×2.4 C.0.26×12 D.2.6×120
【考点】小数乘法.
【专题】计算题;运算能力;应用意识.
【答案】D
【分析】根据积不变的性质,一个因数扩大或缩小几倍(0除外),另一个因数缩小或扩大相同的倍数,积不变。据此解答即可。
【解答】解:列式子中,与2.6×1.2的积不相等的是2.6×120。
故选:D。
【点评】此题考查的目的是理解掌握积不变的性质及应用。
16.(2分)被减数有三位小数,减数有两位小数,差一定是( )位小数。
A.一 B.二 C.三 D.四
【考点】小数的加法和减法.
【专题】计算题;小数的认识;运算能力.
【答案】C
【分析】三位小数减两位小数,差还是三位小数,可举例说明。
【解答】解:如3.221﹣1.22=2.001
故差一定是三位小数。
故选:C。
【点评】用赋值法更能直观的进行说明。
17.(2分)8.743中的“7”表示( )
A.7个十分之一 B.7个0.01
C.7个千分之一
【考点】小数的读写、意义及分类.
【专题】小数的认识.
【答案】A
【分析】首先搞清这个数字在整数的什么数位上和这个数位的计数单位,它就表示有几个这样的计数单位;据此解答.
【解答】解:8.743中的“7”表示7个十分之一.
故选:A.
【点评】此题考查小数、整数中的数字所表示的意义:有几个计数单位;解答时一定要看清数位和这个数位的计数单位.
18.(2分)淘气早上喝一袋牛奶容积是250( )
A.L B.mL C.立方分米
【考点】根据情景选择合适的计量单位.
【专题】长度、面积、体积单位;应用意识.
【答案】B
【分析】根据生活经验以及数据的大小,选择合适的计量单位,即可解答。
【解答】解:淘气早上喝一袋牛奶容积是250毫升。
故选:B。
【点评】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
19.(2分)在﹣3,0,+5,﹣3,+3.1,,2003,+2008中负数有( )
A.2个 B.3个 C.4个
【考点】负数的意义及其应用.
【专题】数的认识.
【答案】B
【分析】负数与正数表示意义相反的量,负数负数用负号“﹣”和一个正数标记,0既不是正数,也不是负数,据此判断即可.
【解答】解:在﹣3,0,+5,﹣3,+3.1,,2003,+2008中负数有3个:
﹣3,﹣3,.
故选:B.
【点评】此题主要考查了正、负数、0的判断,要熟练掌握.
四.判断题(共4小题,满分8分,每小题2分)
20.(2分)一个长9分米、宽5分米的长方形纸板,最多能剪出11个边长是2分米的正方形。 ×
【考点】图形的拼组.
【专题】几何直观.
【答案】×
【分析】根据题干分析可得,分别计算长方形的长和宽分别包含几个正方形的边长,再把它们相乘即可求解。
【解答】解:根据题干分析可得:
9÷2≈4(个)
5÷2≈2(个)
4×2=8(个)
所以多能截出8个这样的正方形。所以原题说法错误。
故答案为:×。
【点评】此题考查了图形的拼组知识,结合题意分析解答即可。
21.(2分)(),利用了乘法的交换律和结合律。 √
【考点】运算定律与简便运算.
【专题】运算能力.
【答案】√
【分析】乘法交换律是指两个数相乘,交换因数的位置,积不变;
乘法结合律是指三个数相乘,可以先把前两个数相乘,再同第三个数相乘,也可以先把后两个数相乘,再同第一个数相乘,结果不变;由此判断即可。
【解答】解:(),是把和交换位置,再把和相结合,利用了乘法的交换律和结合律,说法正确。
故答案为:√。
【点评】本题主要考查了学生对运算定律的熟练掌握情况,牢记定律的内容是关键。
22.(2分)通过割补法把一个平行四边形转化成一个长方形,这个长方形和平行四边形相比,周长和面积都不变。 ×
【考点】平行四边形的面积;平行四边形的周长.
【专题】几何直观;推理能力;应用意识.
【答案】×
【分析】根据平行四边形面积公式的推导过程可知,把一个平行四边形通过割补法转化成一个长方形,这个长方形和平行四边形的面积相等,平行四边形的周长大于长方形的周长。据此判断。
【解答】解:把一个平行四边形通过割补法转化成一个长方形,这个长方形和平行四边形的面积相等,平行四边形的周长大于长方形的周长。
因此,题干中的结论是错误的。
故答案为:×。
【点评】此题考查的目的是理解掌握平行四边形面积公式的推导过程及应用,以及平行四边形、长方形周长的意义及应用。
23.(2分)某城市一天的最高气温为 9°C,最低气温为﹣2°C,该城市当天的温差为 7°C。 ×
【考点】正、负数的运算.
【专题】整数的认识;数据分析观念.
【答案】×
【分析】利用最高温度减去最低温度即可。
【解答】解:9℃﹣(﹣2℃)=11℃
因此这一天的最高气温和最低气温相差11°C。原题说法错误。
故答案为:×。
【点评】本题考查了正负数的运算及生活中的应用。
五.解答题(共1小题,满分6分,每小题6分)
24.(6分)第29届奥林匹克运动会于8月8日在北京举行。赛后金牌数位居前三位的国家获三种奖牌情况如下:
中国 金牌51枚 银牌21枚 铜牌28枚
美国 金牌36枚 银牌38枚 铜牌36枚
俄罗斯 金牌23枚 银牌21枚 铜牌28枚
(1)根据以上资料,完成下面的统计表。
第29届奥运会金牌数位居前三位的国家获奖牌情况统计表
数量/枚 牌别 国别 金牌 银牌 铜牌
合计
中国
美国
俄罗斯
(2)根据上面的有关数据,完成下面的统计图。
【考点】统计图表的填补;绘制条形统计图.
【专题】统计图表的制作与应用;应用意识.
【答案】(1)
数量/枚 牌别 国别 金牌 银牌 铜牌
合计 100 110 72
中国 51 36 23
美国 21 38 21
俄罗斯 28 36 28
(2)
。
【分析】(1)根据统计表记录的数据,用加法分别求出金牌、银牌、铜牌的总和,再填表。
(2)根据统计表中的数据,把统计图中俄罗斯的奖牌的数量补充完整。
【解答】解:(1)51+21+28=100(枚)
36+38+36=110(枚)
23+21+28=72(枚)
统计表如下:
数量/枚 牌别 国别 金牌 银牌 铜牌
合计 100 110 72
中国 51 36 23
美国 21 38 21
俄罗斯 28 36 28
(2)统计图如下:
【点评】本题主要考查了统计表和统计图的填充。
六.解答题(共6小题,满分36分,每小题6分)
25.(6分)把下面各数填入相应的圈里。
﹣4,+13,7,0,,﹣3.2,,88,+27.4,﹣1,﹣34
【考点】负数的意义及其应用.
【专题】整数的认识;数据分析观念.
【答案】
【分析】根据正、负数的意义,数的前面加有“+”号的数,就是正数;数的前面加有“﹣”号的数,就是负数,0既不是正数也不是负数,据此判断即可。
【解答】解:如图:
【点评】此题考查正、负数的意义和分类。
26.(6分)李亮和张红两人同时从家出发相向而行,5分钟后相遇。
(1)用含有字母的式子表示李亮和张红家之间的距离。
(2)当a=75,b=60时,他们两家的距离是多少米?
【考点】含字母式子的求值;用字母表示数.
【专题】用字母表示数;运算能力.
【答案】(1)5(a+b)米;(2)675米。
【分析】(1)路程=速度×时间,据此求出李亮和张红5分钟各自行驶的路程,再将两人行驶的路程相加即可求出李亮和张红家之间的距离;
(2)将a、b的取值代入(1)题的数量关系式即可求出他们两家距离的具体数值。
【解答】解:(1)5×a+5×b
=5a+5b
=5(a+b)(米)
答:用含有字母的式子表示李亮和张红家之间的距离是5(a+b)米。
(2)当a=75,b=60时,
5×(75+60)
=5×135
=675(米)
答:他们两家的距离是675米。
【点评】用字母表示表示数时,数字与字母,字母与字母之间的乘号可以省略,也可以用小圆点“ ”表示;字母与数字相乘时,省略乘号,并且把数字放在字母的前面。当数字是“1”时,“1”常常省略不写;多个字母相乘时,一般按字母顺序书写。
27.(6分)王丽有50元和20元面值的人民币各5张。如果她想买一双200元的鞋子,那么有几种恰好付款200元的方式?
【考点】筛选与枚举.
【专题】压轴题;应用意识.
【答案】按方案①和③这两种付钱,恰好付款200元。
【分析】50元的最多用:200÷50=4(张),然后从4张开始分别列举即可。
【解答】解:
付钱方案 50元 20元 总额
① 4张 0张 200元√
② 3张 3张 210元
③ 2张 5张 200元√
答:可以按方案①和③这两种付钱,恰好付款200元。
【点评】此题是较复杂的筛选与枚举问题,要弄清题意,分情况分析推理。
28.(6分)李叔叔从家坐出租车去公司共花了24.5元,李叔叔家距离公司多少千米?(不足1千米按1千米计算)
【考点】整数、小数复合应用题.
【专题】简单应用题和一般复合应用题;应用意识.
【答案】8千米。
【分析】李叔叔一共花的钱数减去3千米内收的钱数,求出超出部分收的钱数,再用超出部分收的钱数除以超出部分每千米的收费数,求出超出3千米的路程,最后加上3千米即为李叔叔家距离公司的千米数。
【解答】解:24.5﹣12.5=12(元)
12÷2.4=5(千米)
3+5=8(千米)
答:李叔叔家距离公司8千米。
【点评】本题考查分段付费问题,先求出超出3千米部分的千米数是解题的关键。
29.(6分)把一个边长是6分米的正方形铁丝框架拆开,用这些铁丝围成一个最大的等边三角形,这个等边三角形的边长是多少分米?
【考点】三角形的周长和面积;正方形的周长.
【专题】数的运算.
【答案】8分米。
【分析】根据正方形的周长=边长×4,求出铁丝的长,再除以3即可。
【解答】解:6×4÷3
=24÷3
=8(分米)
答:这个等边三角形的边长是8分米。
【点评】熟练掌握正方形的周长公式和等边三角形的性质,是解答此题的关键。
30.(6分)下图是某学校2019年春季达标运动会六年级(1)~(4)班体育达标情况统计图。
六年级(1)~(4)班体育达标情况统计图
请根据统计图中的信息完成上面的统计表,并回答下面的问题。
1.达标率最高的班级是( )达标率最低的班级是( )。
2.四个班的总人数是( )人,达标人数一共有( )人,估算总体达标率约为( )%。
【考点】统计图表的填补;从统计图表中获取信息;两种不同形式的复式条形统计图.
【专题】数据分析观念.
【答案】
1.六(3),六(4);
2.195,106,54.4。
【分析】用每班的达标人数除以全班人数分别求出达标率,至此即可完成统计表;
1.比较百分数的大小,最大的百分数就是达标率最高的班级,最小的百分数的就是达标率最低的班级;
2.把四个班的全班人数加起来的和就是四个班的总人数,把四个班的达标人数加起来的和就是一共达标的人数,一共达标的人数除以四个班的总人数可求出总体达标率。
【解答】解:各班达标率分别为:
27÷45=60%
21÷50=42%
38÷50=76%
20÷50=40%
根据统计图中的数据完成统计表如下:
1.76%>60%>42%>40%
答:达标率最高的班级是六(3)班,达标率最低的班级是六(4)班。
2.45+50×3
=45+150
=195(人)
27+21+38+20=106(人)
106÷195≈54.4%
答:四个班的总人数是195人,达标人数一共有106人,估算总体达标率约为54.4%。
【点评】本题考查了条形统计图的认识,根据条形统计图正确进行分析可解答问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
江苏省南京市2025-2026学年五年级上学期期末模拟数学预测卷
一.计算题(共3小题,满分18分,每小题6分)
1.(6分)直接写得数。
2.5÷5= 75÷2.5= 6.2×2= 8÷3=
10.5÷0.5= 12÷11= 5.9﹣0.9= 6.06÷0.01=
2.(6分)计算下面各题,能简便的要用简便方法算。
(1)1.25×7.9×0.8 (2)63÷(1.7+1.9)+4.8
(3)8.4×13.5﹣3.5×8.4 (4)9.2÷0.25÷0.4
3.(6分)如图,在大正方形中,已知两个长方形的面积分别为15m2和40m2,求阴影正方形的面积。(请写出主要过程)
二.填空题(共8小题,满分16分,每小题2分)
4.(2分)体育老师对六年级女生进行了仰卧起坐的测验。每分钟19个为及格,记作0。小红的成绩记作+3,则她仰卧起坐的个数是 个。
5.(2分)亮亮今年12岁,比爸爸小m岁。5年后爸爸的年龄用含有字母的式子表示为 岁。
6.(2分)12支球队参加比赛,如果每2个球队之间进行一次比赛,至少要比赛 场。
7.(2分)如图是江海市实行垃圾分类以来的垃圾整理情况统计图。
(1)2022年江海市产生的垃圾总量是 万吨。
(2)2023年江海市已分类垃圾比2020年多 万吨,未分类垃圾比2020年少 万吨。
8.(2分)淘气时走3千米,平均每时走 千米,平均每千米用 时。
9.(2分)把9.86的小数点去掉,得到的新数比原数多 .
10.(2分)在空里写出合适的小数。
阴影部分用小数表示是
箭头表示的数是
11.(2分)长方形面积= ×
正方形面积= ×
三.选择题(共8小题,满分16分,每小题2分)
12.(2分)老刘今年a岁,小刘今年(a﹣14)岁,再过c年后,他们相差的岁数是( )
A.14岁 B.c岁 C.(c+14)岁
13.(2分)有5个球队参加比赛,如果每两个球队之间都要进行一场比赛,一共要比赛( )场。
A.10 B.8 C.6 D.5
14.(2分)铁道部门规定,儿童身高在120厘米以下乘火车免票,120~150厘米享受半价票,150厘米以上需购买全价票。蓝天小学合唱队乘火车去外地演出,队员身高情况统计如下表,如果把队员从矮到高排序,张强排在第16位,他的情况是( )
身高/厘米 120以下 120~150 150以上
人数 2 13 5
A.免票 B.购买半价票
C.购买全价票
15.(2分)下列式子中,与2.6×1.2的积不相等的是( )
A.26×0.12 B.1.3×2.4 C.0.26×12 D.2.6×120
16.(2分)被减数有三位小数,减数有两位小数,差一定是( )位小数。
A.一 B.二 C.三 D.四
17.(2分)8.743中的“7”表示( )
A.7个十分之一 B.7个0.01
C.7个千分之一
18.(2分)淘气早上喝一袋牛奶容积是250( )
A.L B.mL C.立方分米
19.(2分)在﹣3,0,+5,﹣3,+3.1,,2003,+2008中负数有( )
A.2个 B.3个 C.4个
四.判断题(共4小题,满分8分,每小题2分)
20.(2分)一个长9分米、宽5分米的长方形纸板,最多能剪出11个边长是2分米的正方形。
21.(2分)(),利用了乘法的交换律和结合律。
22.(2分)通过割补法把一个平行四边形转化成一个长方形,这个长方形和平行四边形相比,周长和面积都不变。
23.(2分)某城市一天的最高气温为 9°C,最低气温为﹣2°C,该城市当天的温差为 7°C。
五.作图题(共1小题,满分6分,每小题6分)
24.(6分)第29届奥林匹克运动会于8月8日在北京举行。赛后金牌数位居前三位的国家获三种奖牌情况如下:
中国 金牌51枚 银牌21枚 铜牌28枚
美国 金牌36枚 银牌38枚 铜牌36枚
俄罗斯 金牌23枚 银牌21枚 铜牌28枚
(1)根据以上资料,完成下面的统计表。
第29届奥运会金牌数位居前三位的国家获奖牌情况统计表
数量/枚 牌别 国别 金牌 银牌 铜牌
合计
中国
美国
俄罗斯
(2)根据上面的有关数据,完成下面的统计图。
六.解答题(共6小题,满分36分,每小题6分)
25.(6分)把下面各数填入相应的圈里。
﹣4,+13,7,0,,﹣3.2,,88,+27.4,﹣1,﹣34
26.(6分)李亮和张红两人同时从家出发相向而行,5分钟后相遇。
(1)用含有字母的式子表示李亮和张红家之间的距离。
(2)当a=75,b=60时,他们两家的距离是多少米?
27.(6分)王丽有50元和20元面值的人民币各5张。如果她想买一双200元的鞋子,那么有几种恰好付款200元的方式?
28.(6分)李叔叔从家坐出租车去公司共花了24.5元,李叔叔家距离公司多少千米?(不足1千米按1千米计算)
29.(6分)把一个边长是6分米的正方形铁丝框架拆开,用这些铁丝围成一个最大的等边三角形,这个等边三角形的边长是多少分米?
30.(6分)下图是某学校2019年春季达标运动会六年级(1)~(4)班体育达标情况统计图。
六年级(1)~(4)班体育达标情况统计图
请根据统计图中的信息完成上面的统计表,并回答下面的问题。
1.达标率最高的班级是( )达标率最低的班级是( )。
2.四个班的总人数是( )人,达标人数一共有( )人,估算总体达标率约为( )%。
参考答案与试题解析
计算题(共3小题,满分18分,每小题6分)
1.(6分)直接写得数。
2.5÷5= 75÷2.5= 6.2×2= 8÷3=
10.5÷0.5= 12÷11= 5.9﹣0.9= 6.06÷0.01=
【考点】小数除法;小数乘小数;小数乘法.
【专题】运算能力.
【答案】0.5;30;12.4;2.;21;1.;5;606。
【分析】根据小数减法、小数乘法、小数除法的运算法则直接写出得数即可。
【解答】解:
2.5÷5=0.5 75÷2.5=30 6.2×2=12.4 8÷3=2.
10.5÷0.5=21 12÷11=1. 5.9﹣0.9=5 6.06÷0.01=606
【点评】本题主要考查了小数减法、小数乘法、小数除法的运算,属于基本的计算,在平时注意积累经验,逐步提高运算的速度和准确性。
2.(6分)计算下面各题,能简便的要用简便方法算。
(1)1.25×7.9×0.8 (2)63÷(1.7+1.9)+4.8
(3)8.4×13.5﹣3.5×8.4 (4)9.2÷0.25÷0.4
【考点】小数乘法(推广整数乘法运算定律);小数四则混合运算;运算定律与简便运算.
【专题】数的运算;运算能力.
【答案】(1)7.9;
(2)22.3;
(3)84;
(4)92
【分析】(1)运用乘法的交换律、结合律进行简便计算。
(2)按照小数四则混合运算的顺序计算。
(3)运用乘法的分配律进行简便计算。
(4)根据除法的性质进行简算。
【解答】解:(1)1.25×7.9×0.8
=(1.25×0.8)×7.9
=1×7.9
=7.9
(2)63÷(1.7+1.9)+4.8
=63÷3.6+4.8
=17.5+4.8
=22.3
(3)8.4×13.5﹣3.5×8.4
=8.4×(13.5﹣3.5)
=8.4×10
=84
(4)9.2÷0.25÷0.4
=9.2÷(0.25×0.4)
=9.2÷0.1
=92
【点评】本题考查了运用运算定律进行简便计算和小数的四则混合运算。
3.(6分)如图,在大正方形中,已知两个长方形的面积分别为15m2和40m2,求阴影正方形的面积。(请写出主要过程)
【考点】组合图形的面积.
【专题】综合题;几何直观.
【答案】15的因数有1、3、5、15,40的因数有1、2、5、8、20、40,3×5=15,5×8=40,3+5=8(厘米),阴影正方形的边长是3厘米,3×3=9(平方厘米)。
【分析】依据题意结合图示可知,15的因数有1、3、5、15,40的因数有1、2、5、8、20、40,利用长方形的面积=长×宽,正方形的特点去解答。
【解答】解:15的因数有1、3、5、15,40的因数有1、2、5、8、20、40,3×5=15,5×8=40,3+5=8(厘米),阴影正方形的边长是3厘米,3×3=9(平方厘米)。
【点评】本题考查的是组合图形的面积的应用。
二.填空题(共8小题,满分16分,每小题2分)
4.(2分)体育老师对六年级女生进行了仰卧起坐的测验。每分钟19个为及格,记作0。小红的成绩记作+3,则她仰卧起坐的个数是 22 个。
【考点】负数的意义及其应用.
【答案】22。
【分析】用正负数表示意义相反的两种量:高于19分记作正,则低于19分就记作负。由此得解。
【解答】解:19+3=22(个)
答:小红的成绩记作+3,则她仰卧起坐的个数是22个。
故答案为:22。
【点评】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
5.(2分)亮亮今年12岁,比爸爸小m岁。5年后爸爸的年龄用含有字母的式子表示为 17+m 岁。
【考点】用字母表示数.
【专题】用字母表示数;应用意识.
【答案】17+m。
【分析】亮亮的年龄加上亮亮比爸爸小的年龄,求出爸爸今年的年龄,再用爸爸今年的年龄加上5,求出5年后爸爸的年龄。
【解答】解:12+m+5=17+m
答:5年后爸爸的年龄用含有字母的式子表示为(17+m)岁。
故答案为:17+m。
【点评】本题考查用字母表示数,明确数量间的关系是解题的关键。
6.(2分)12支球队参加比赛,如果每2个球队之间进行一次比赛,至少要比赛 66 场。
【考点】握手问题.
【专题】推理能力;应用意识.
【答案】66。
【分析】每两个队之间赛一场,那么每个队要赛11场,一共是(11×12)场,但是两队比赛是同一场比赛,所以(11×12)场比赛就多算了一倍,再除以2即可。
【解答】解:12×(12﹣1)÷2
=132÷2
=66(场)
答:至少要比赛66场。
故答案为:66。
【点评】本题属于握手问题,可利用握手问题的公式求解:握手次数=人数×(人数﹣1)÷2进行求解。
7.(2分)如图是江海市自2020年实行垃圾分类以来的垃圾整理情况统计图。
(1)2022年江海市产生的垃圾总量是 756 万吨。
(2)2023年江海市已分类垃圾比2020年多 130 万吨,未分类垃圾比2020年少 15 万吨。
【考点】以一当五(或以上)的条形统计图;从统计图表中获取信息.
【专题】综合填空题;应用意识.
【答案】(1)756;
(2)130,15。
【分析】(1)依据统计图用加法列式计算2022年江海市产生的垃圾总量;
(2)用减法列式计算2023年江海市已分类垃圾比2020年多多少万吨,用减法列式计算未分类垃圾比2020年少多少万吨。
【解答】解:(1)696+60=756(万吨)
答:2022年江海市产生的垃圾总量756万吨。
(2)724﹣594=130(万吨)
71﹣56=15(万吨)
答:2023年江海市已分类垃圾比2020年多130万吨,未分类垃圾比2020年少15万吨。
故答案为:(1)756;(2)130,15。
【点评】本题考查的是统计图的应用。
8.(2分)淘气时走3千米,平均每时走 千米,平均每千米用 时。
【考点】简单的行程问题.
【专题】应用题;数据分析观念.
【答案】,。
【分析】根据“淘气时走3千米”可根据“速度=路程÷时间”代入数值,求出淘气每小时走的路程,已知淘气走了1千米,可根据“时间=路程÷速度”对应数值求出平均每千米需要的时间,据此解答。
【解答】解:3(千米)
1(时)
答:平均每时走千米,平均每千米用时。
故答案为:,。
【点评】此题主要考查路程、速度、时间三者的关系式:路程=速度×时间,速度=路程÷时间,时间=路程÷速度,灵活变形列式解决问题。
9.(2分)把9.86的小数点去掉,得到的新数比原数多 976.14 .
【考点】小数的加法和减法.
【专题】文字叙述题.
【答案】见试题解答内容
【分析】9.86去掉小数点后是986,它比原数多多少,只要再减去原数即可.
【解答】解:986﹣9.86=976.14.
答:得到的新数比原数多976.14.
故答案为:976.14.
【点评】本题的重点是求出去掉小数点后的新数,再根据减法的意义解答.
10.(2分)在空里写出合适的小数。
阴影部分用小数表示是 1.4
箭头表示的数是 0.8
【考点】小数的读写、意义及分类.
【专题】数感.
【答案】1.4,0.8。
【分析】把整个图形看作单位“1”平均分成10份,每份表示0.1,则题中的阴影部分用小数表示为1.4;
把1平均分成10份,每份表示0.1,所以箭头表示的数是 0.8;由此解答即可。
【解答】解:阴影部分用小数表示是 1.4
箭头表示的数是 0.8
故答案为:1.4,0.8。
【点评】此题考查小数的意义和表示方法,明确每个单位长度表示多少,是解答此题的关键。
11.(2分)长方形面积= 长 × 宽
正方形面积= 边长 × 边长
【考点】长方形、正方形的面积.
【专题】应用意识.
【答案】长,宽,边长,边长。
【分析】根据长方形、正方形的面积公式解答即可。
【解答】解:长方形的面积=长×宽,正方形的面积=边长×边长。
故答案为:长,宽,边长,边长。
【点评】此题考查的目的是理解掌握长方形、正方形的面积公式及应用。
三.选择题(共8小题,满分16分,每小题2分)
12.(2分)老刘今年a岁,小刘今年(a﹣14)岁,再过c年后,他们相差的岁数是( )
A.14岁 B.c岁 C.(c+14)岁
【考点】年龄问题;用字母表示数.
【专题】综合填空题;设数法;年龄问题.
【答案】A
【分析】因为年龄差是一个不变的数值,所以老王和小李c年后的年龄差,也就是今年的年龄差.
【解答】解:a﹣(a﹣14)=14(岁)
现在相差14岁,c年后还是相差19岁.
答:再过c年后,他们相差的岁数是14岁.
故选:A.
【点评】此题考查年龄问题,要注意:两个人的年龄差是一个永远也不变的数值.
13.(2分)有5个球队参加比赛,如果每两个球队之间都要进行一场比赛,一共要比赛( )场。
A.10 B.8 C.6 D.5
【考点】排列组合;握手问题.
【专题】压轴题;应用意识.
【答案】A
【分析】如果每两个球队之间都要进行一场比赛,相当于两两组合,根据握手问题的公式n(n﹣1)÷2解答即可。
【解答】解:5×(5﹣1)÷2
=20÷2
=10(场)
答:一共要比赛10场。
故选:A。
【点评】本题考查了握手问题的实际应用,要注意去掉重复计算的情况,如果数量比较少可以用枚举法解答,如果数量比较多可以用公式n(n﹣1)÷2解答。
14.(2分)铁道部门规定,儿童身高在120厘米以下乘火车免票,120~150厘米享受半价票,150厘米以上需购买全价票。蓝天小学合唱队乘火车去外地演出,队员身高情况统计如下表,如果把队员从矮到高排序,张强排在第16位,他的情况是( )
身高/厘米 120以下 120~150 150以上
人数 2 13 5
A.免票 B.购买半价票
C.购买全价票
【考点】从统计图表中获取信息.
【专题】应用题;应用意识.
【答案】C
【分析】通过观察统计表可知,蓝天小学合唱队共有20人,其中120厘米以下的有2人,150厘米以上的5人,把合唱队员从矮到高排成一排,张强排在第16位,由此可知,张强的身高在150厘米以上,所以按规定张强应购买全价票。据此解答。
【解答】解:蓝天小学合唱队共有20人,其中120厘米以下的有2人,150厘米以上的5人,把合唱队员从矮到高排成一排,张强排在第16位,由此可知,张强的身高在150厘米以上,所以按规定张强应购买全价票。
故选:C。
【点评】本题考查的目的是理解掌握统计表的特点及作用,并且能够根据统计表提供的信息,解决有关的实际问题。
15.(2分)下列式子中,与2.6×1.2的积不相等的是( )
A.26×0.12 B.1.3×2.4 C.0.26×12 D.2.6×120
【考点】小数乘法.
【专题】计算题;运算能力;应用意识.
【答案】D
【分析】根据积不变的性质,一个因数扩大或缩小几倍(0除外),另一个因数缩小或扩大相同的倍数,积不变。据此解答即可。
【解答】解:列式子中,与2.6×1.2的积不相等的是2.6×120。
故选:D。
【点评】此题考查的目的是理解掌握积不变的性质及应用。
16.(2分)被减数有三位小数,减数有两位小数,差一定是( )位小数。
A.一 B.二 C.三 D.四
【考点】小数的加法和减法.
【专题】计算题;小数的认识;运算能力.
【答案】C
【分析】三位小数减两位小数,差还是三位小数,可举例说明。
【解答】解:如3.221﹣1.22=2.001
故差一定是三位小数。
故选:C。
【点评】用赋值法更能直观的进行说明。
17.(2分)8.743中的“7”表示( )
A.7个十分之一 B.7个0.01
C.7个千分之一
【考点】小数的读写、意义及分类.
【专题】小数的认识.
【答案】A
【分析】首先搞清这个数字在整数的什么数位上和这个数位的计数单位,它就表示有几个这样的计数单位;据此解答.
【解答】解:8.743中的“7”表示7个十分之一.
故选:A.
【点评】此题考查小数、整数中的数字所表示的意义:有几个计数单位;解答时一定要看清数位和这个数位的计数单位.
18.(2分)淘气早上喝一袋牛奶容积是250( )
A.L B.mL C.立方分米
【考点】根据情景选择合适的计量单位.
【专题】长度、面积、体积单位;应用意识.
【答案】B
【分析】根据生活经验以及数据的大小,选择合适的计量单位,即可解答。
【解答】解:淘气早上喝一袋牛奶容积是250毫升。
故选:B。
【点评】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
19.(2分)在﹣3,0,+5,﹣3,+3.1,,2003,+2008中负数有( )
A.2个 B.3个 C.4个
【考点】负数的意义及其应用.
【专题】数的认识.
【答案】B
【分析】负数与正数表示意义相反的量,负数负数用负号“﹣”和一个正数标记,0既不是正数,也不是负数,据此判断即可.
【解答】解:在﹣3,0,+5,﹣3,+3.1,,2003,+2008中负数有3个:
﹣3,﹣3,.
故选:B.
【点评】此题主要考查了正、负数、0的判断,要熟练掌握.
四.判断题(共4小题,满分8分,每小题2分)
20.(2分)一个长9分米、宽5分米的长方形纸板,最多能剪出11个边长是2分米的正方形。 ×
【考点】图形的拼组.
【专题】几何直观.
【答案】×
【分析】根据题干分析可得,分别计算长方形的长和宽分别包含几个正方形的边长,再把它们相乘即可求解。
【解答】解:根据题干分析可得:
9÷2≈4(个)
5÷2≈2(个)
4×2=8(个)
所以多能截出8个这样的正方形。所以原题说法错误。
故答案为:×。
【点评】此题考查了图形的拼组知识,结合题意分析解答即可。
21.(2分)(),利用了乘法的交换律和结合律。 √
【考点】运算定律与简便运算.
【专题】运算能力.
【答案】√
【分析】乘法交换律是指两个数相乘,交换因数的位置,积不变;
乘法结合律是指三个数相乘,可以先把前两个数相乘,再同第三个数相乘,也可以先把后两个数相乘,再同第一个数相乘,结果不变;由此判断即可。
【解答】解:(),是把和交换位置,再把和相结合,利用了乘法的交换律和结合律,说法正确。
故答案为:√。
【点评】本题主要考查了学生对运算定律的熟练掌握情况,牢记定律的内容是关键。
22.(2分)通过割补法把一个平行四边形转化成一个长方形,这个长方形和平行四边形相比,周长和面积都不变。 ×
【考点】平行四边形的面积;平行四边形的周长.
【专题】几何直观;推理能力;应用意识.
【答案】×
【分析】根据平行四边形面积公式的推导过程可知,把一个平行四边形通过割补法转化成一个长方形,这个长方形和平行四边形的面积相等,平行四边形的周长大于长方形的周长。据此判断。
【解答】解:把一个平行四边形通过割补法转化成一个长方形,这个长方形和平行四边形的面积相等,平行四边形的周长大于长方形的周长。
因此,题干中的结论是错误的。
故答案为:×。
【点评】此题考查的目的是理解掌握平行四边形面积公式的推导过程及应用,以及平行四边形、长方形周长的意义及应用。
23.(2分)某城市一天的最高气温为 9°C,最低气温为﹣2°C,该城市当天的温差为 7°C。 ×
【考点】正、负数的运算.
【专题】整数的认识;数据分析观念.
【答案】×
【分析】利用最高温度减去最低温度即可。
【解答】解:9℃﹣(﹣2℃)=11℃
因此这一天的最高气温和最低气温相差11°C。原题说法错误。
故答案为:×。
【点评】本题考查了正负数的运算及生活中的应用。
五.解答题(共1小题,满分6分,每小题6分)
24.(6分)第29届奥林匹克运动会于8月8日在北京举行。赛后金牌数位居前三位的国家获三种奖牌情况如下:
中国 金牌51枚 银牌21枚 铜牌28枚
美国 金牌36枚 银牌38枚 铜牌36枚
俄罗斯 金牌23枚 银牌21枚 铜牌28枚
(1)根据以上资料,完成下面的统计表。
第29届奥运会金牌数位居前三位的国家获奖牌情况统计表
数量/枚 牌别 国别 金牌 银牌 铜牌
合计
中国
美国
俄罗斯
(2)根据上面的有关数据,完成下面的统计图。
【考点】统计图表的填补;绘制条形统计图.
【专题】统计图表的制作与应用;应用意识.
【答案】(1)
数量/枚 牌别 国别 金牌 银牌 铜牌
合计 100 110 72
中国 51 36 23
美国 21 38 21
俄罗斯 28 36 28
(2)
。
【分析】(1)根据统计表记录的数据,用加法分别求出金牌、银牌、铜牌的总和,再填表。
(2)根据统计表中的数据,把统计图中俄罗斯的奖牌的数量补充完整。
【解答】解:(1)51+21+28=100(枚)
36+38+36=110(枚)
23+21+28=72(枚)
统计表如下:
数量/枚 牌别 国别 金牌 银牌 铜牌
合计 100 110 72
中国 51 36 23
美国 21 38 21
俄罗斯 28 36 28
(2)统计图如下:
【点评】本题主要考查了统计表和统计图的填充。
六.解答题(共6小题,满分36分,每小题6分)
25.(6分)把下面各数填入相应的圈里。
﹣4,+13,7,0,,﹣3.2,,88,+27.4,﹣1,﹣34
【考点】负数的意义及其应用.
【专题】整数的认识;数据分析观念.
【答案】
【分析】根据正、负数的意义,数的前面加有“+”号的数,就是正数;数的前面加有“﹣”号的数,就是负数,0既不是正数也不是负数,据此判断即可。
【解答】解:如图:
【点评】此题考查正、负数的意义和分类。
26.(6分)李亮和张红两人同时从家出发相向而行,5分钟后相遇。
(1)用含有字母的式子表示李亮和张红家之间的距离。
(2)当a=75,b=60时,他们两家的距离是多少米?
【考点】含字母式子的求值;用字母表示数.
【专题】用字母表示数;运算能力.
【答案】(1)5(a+b)米;(2)675米。
【分析】(1)路程=速度×时间,据此求出李亮和张红5分钟各自行驶的路程,再将两人行驶的路程相加即可求出李亮和张红家之间的距离;
(2)将a、b的取值代入(1)题的数量关系式即可求出他们两家距离的具体数值。
【解答】解:(1)5×a+5×b
=5a+5b
=5(a+b)(米)
答:用含有字母的式子表示李亮和张红家之间的距离是5(a+b)米。
(2)当a=75,b=60时,
5×(75+60)
=5×135
=675(米)
答:他们两家的距离是675米。
【点评】用字母表示表示数时,数字与字母,字母与字母之间的乘号可以省略,也可以用小圆点“ ”表示;字母与数字相乘时,省略乘号,并且把数字放在字母的前面。当数字是“1”时,“1”常常省略不写;多个字母相乘时,一般按字母顺序书写。
27.(6分)王丽有50元和20元面值的人民币各5张。如果她想买一双200元的鞋子,那么有几种恰好付款200元的方式?
【考点】筛选与枚举.
【专题】压轴题;应用意识.
【答案】按方案①和③这两种付钱,恰好付款200元。
【分析】50元的最多用:200÷50=4(张),然后从4张开始分别列举即可。
【解答】解:
付钱方案 50元 20元 总额
① 4张 0张 200元√
② 3张 3张 210元
③ 2张 5张 200元√
答:可以按方案①和③这两种付钱,恰好付款200元。
【点评】此题是较复杂的筛选与枚举问题,要弄清题意,分情况分析推理。
28.(6分)李叔叔从家坐出租车去公司共花了24.5元,李叔叔家距离公司多少千米?(不足1千米按1千米计算)
【考点】整数、小数复合应用题.
【专题】简单应用题和一般复合应用题;应用意识.
【答案】8千米。
【分析】李叔叔一共花的钱数减去3千米内收的钱数,求出超出部分收的钱数,再用超出部分收的钱数除以超出部分每千米的收费数,求出超出3千米的路程,最后加上3千米即为李叔叔家距离公司的千米数。
【解答】解:24.5﹣12.5=12(元)
12÷2.4=5(千米)
3+5=8(千米)
答:李叔叔家距离公司8千米。
【点评】本题考查分段付费问题,先求出超出3千米部分的千米数是解题的关键。
29.(6分)把一个边长是6分米的正方形铁丝框架拆开,用这些铁丝围成一个最大的等边三角形,这个等边三角形的边长是多少分米?
【考点】三角形的周长和面积;正方形的周长.
【专题】数的运算.
【答案】8分米。
【分析】根据正方形的周长=边长×4,求出铁丝的长,再除以3即可。
【解答】解:6×4÷3
=24÷3
=8(分米)
答:这个等边三角形的边长是8分米。
【点评】熟练掌握正方形的周长公式和等边三角形的性质,是解答此题的关键。
30.(6分)下图是某学校2019年春季达标运动会六年级(1)~(4)班体育达标情况统计图。
六年级(1)~(4)班体育达标情况统计图
请根据统计图中的信息完成上面的统计表,并回答下面的问题。
1.达标率最高的班级是( )达标率最低的班级是( )。
2.四个班的总人数是( )人,达标人数一共有( )人,估算总体达标率约为( )%。
【考点】统计图表的填补;从统计图表中获取信息;两种不同形式的复式条形统计图.
【专题】数据分析观念.
【答案】
1.六(3),六(4);
2.195,106,54.4。
【分析】用每班的达标人数除以全班人数分别求出达标率,至此即可完成统计表;
1.比较百分数的大小,最大的百分数就是达标率最高的班级,最小的百分数的就是达标率最低的班级;
2.把四个班的全班人数加起来的和就是四个班的总人数,把四个班的达标人数加起来的和就是一共达标的人数,一共达标的人数除以四个班的总人数可求出总体达标率。
【解答】解:各班达标率分别为:
27÷45=60%
21÷50=42%
38÷50=76%
20÷50=40%
根据统计图中的数据完成统计表如下:
1.76%>60%>42%>40%
答:达标率最高的班级是六(3)班,达标率最低的班级是六(4)班。
2.45+50×3
=45+150
=195(人)
27+21+38+20=106(人)
106÷195≈54.4%
答:四个班的总人数是195人,达标人数一共有106人,估算总体达标率约为54.4%。
【点评】本题考查了条形统计图的认识,根据条形统计图正确进行分析可解答问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
