【期末押题卷】江苏省南京市2025-2026学年六年级上学期期末模拟数学预测卷苏教版(含解析)
文档属性
| 名称 | 【期末押题卷】江苏省南京市2025-2026学年六年级上学期期末模拟数学预测卷苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 515.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 22:24:03 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
江苏省南京市2025-2026学年六年级上学期期末模拟数学预测卷
一.选择题(共6小题,满分12分,每小题2分)
1.(2分)下列( )个图形能折成正方体.
A. B. C.
2.(2分)下面与:的比值相等的比是( )
A.0.5:0.4 B.5:4 C.20:25
3.(2分)20cm增加后是( )cm。
A. B.24 C.25 D.30
4.(2分)如果一个圆柱的侧面展开图是一个正方形,那么该图柱的高和底面周长的比是( )
A.2π:1 B.1:π C.1:1 D.π:1
5.(2分)平行四边形和三角形的高相等,面积也相等,平行四边形的底是20厘米,三角形的底是( )
A.10厘米 B.20厘米 C.40厘米
6.(2分)有两个杯子,甲杯有100克水,乙杯有90克水.往甲杯中放25克糖,往乙杯中放20克糖,则两杯水相比较,( )
A.甲杯甜 B.乙杯甜 C.一样甜
二.解答题(共12小题,满分23分)
7.(4分) :1580%= ÷40= (填小数)= (成数)
8.(2分)24千克的是 千克;24千克比 千克多。
9.(2分)一个长8米、宽6米、高5米的长方体,占地面积最小是 平方米,这个长方体的棱长之和是 米,表面积是 平方米,体积是 立方米。
10.(2分)一台拖拉机小时耕地公顷,这台拖拉机1小时耕地 公顷;耕地1公顷需要 小时。
11.(2分)某种电器原售价500元,三月初涨价10%,四月初又在三月初的基础上降价20%。现在这款电器的售价为 元。
12.(1分)在400g盐水中,含盐80g,盐占盐水的 %。
13.(1分)2022年春节佳佳把2500元压岁钱存入银行,整存整取两年,年利率3.75%,到期时佳佳可以从银行中取出 元。
14.(2分)一本科技书有240页,张明第一天看了这本书的,第二天看了这本书的,张明两天看了 页,第三天应从第 页看起。
15.(2分)10克盐加入到40克水中,盐占盐水的 %,水与盐水的比为 。
16.(3分)学校三、四、五年级学生共100人参加植树活动,共植树566棵。已知三、四年级的人数相等,三年级学生平均每人植树4棵,四年级学生平均每人植树5棵,五年级学生平均每人植树6.5棵。三年级学生共植树 棵。
17.(1分)淘气在看一本90页的《七彩阳光》,已经看了一周,还剩27页没看。过去的一周他平均每天看 页。
18.(1分)甲、乙两筐西瓜共重360千克,从甲筐取出放入乙筐,两筐西瓜就一样重.原来甲筐西瓜重 千克,乙筐西瓜重 千克。
三.计算题(共4小题,满分35分)
19.(8分)直接写出得数。
106﹣97= 0.72÷0.4=
2.5×0.6= 0.19+0.76= 0.1﹣0.01= 0.33=
20.(12分)计算下面各题,能简算的要简算。
(1) (2) (3)40
(4)5136 (5)()×9×10 (6)2025
21.(9分)解方程。
70%x=5.6
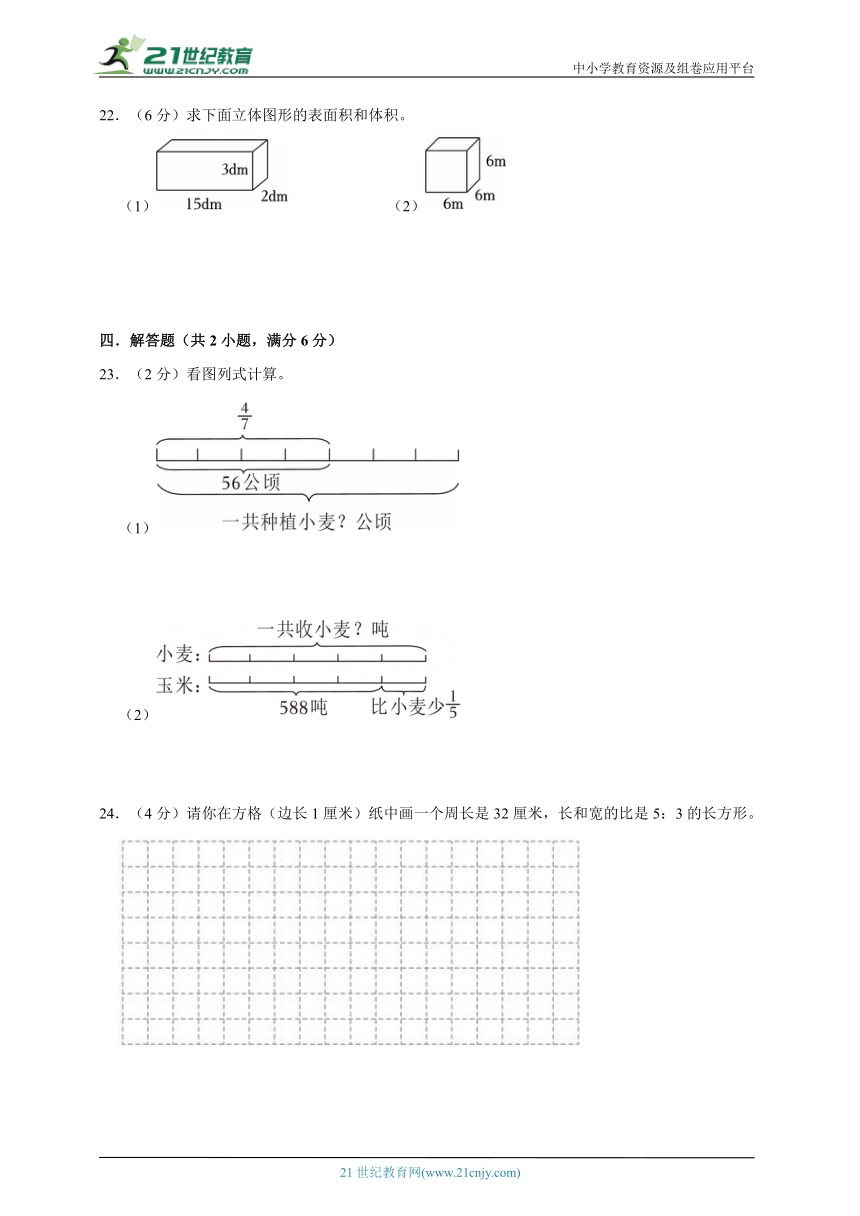
22.(6分)求下面立体图形的表面积和体积。
(1) (2)
四.解答题(共2小题,满分6分)
23.(2分)看图列式计算。
(1)
24.(4分)请你在方格(边长1厘米)纸中画一个周长是32厘米,长和宽的比是5:3的长方形。
五.解答题(共6小题,满分24分)
25.(5分)一个长方体文具盒,底面积是200cm2,高是3cm,这个文具盒的体积是多少立方厘米?合多少立方分米?
26.(4分)学校图书室今年有图书2760册,比去年图书数量增加了15%。学校图书室去年有图书多少册?
27.(4分)某电脑商店四周卖出一批电脑,第一周卖出总台数的,第二周卖出总台数的,第三周与第四周卖出的台数比是5:2,已知第四周比第三周少卖出了180台,第三周和第四周一共卖出了多少台?这批电脑原有多少台?
28.(4分)笑笑读一本故事书,已读页数是全书的,如果再读14页,这时已读页数和全书的页数之比是3:8,这本书共有多少页?
29.(4分)某校语文老师、科学老师、音乐老师的人数比是15:3:2,如果该校音乐老师有6人,那么语文老师和科学老师各有多少人?
30.(3分)有一块边长2米的正方形铁板,把它锯成一个最大的圆,面积会比原来减少百分之几?
参考答案与试题解析
一.选择题(共6小题,满分12分,每小题2分)
1.(2分)下列( )个图形能折成正方体.
A. B. C.
【考点】正方体的展开图.
【专题】作图题;图形与变换.
【答案】B
【分析】根据正方体展开图的11种特征,选项A和选项C不属于正方体展开图,不能折成正方体;选项B属于正方体展开图的“1﹣4﹣1”型,能折成正方体.
【解答】解:根据正方体展开图的特征,选项A和选项C不能折成正方体;选项B能折成正方体.
故选:B.
【点评】正方体展开图有11种特征,分四种类型,即:第一种:“1﹣4﹣1”结构,即第一行放1个,第二行放4个,第三行放1个;第二种:“2﹣2﹣2”结构,即每一行放2个正方形,此种结构只有一种展开图;第三种:“3﹣3”结构,即每一行放3个正方形,只有一种展开图;第四种:“1﹣3﹣2”结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形.
2.(2分)下面与:的比值相等的比是( )
A.0.5:0.4 B.5:4 C.20:25
【考点】求比值和化简比.
【专题】比和比例;运算能力.
【答案】C
【分析】先用比:的前项除以后项,得出比值,再用同样的方法求出每一个选项中比的比值,进而找出与:的比值相等的比得解.
【解答】解::
A、0.5:0.4=0.5÷0.4,因为,所以不符合题意
B、5:4=5÷4,因为,所以不符合题意
C、20:25=20÷25,因为,所以符合题意.
故选:C.
【点评】此题考查学生求比值的方法的运用.
3.(2分)20cm增加后是( )cm。
A. B.24 C.25 D.30
【考点】分数乘法.
【专题】应用意识.
【答案】B
【分析】将20厘米看作单位“1”,用20厘米乘(1),即可求出20厘米增加后是多少厘米,据此解答。
【解答】解:20×(1)
=20
=24(cm)
答:20cm增加后是24cm。
故选:B。
【点评】求比一个数多这个数的几分之几是多少,用乘加混合运算解答。
4.(2分)如果一个圆柱的侧面展开图是一个正方形,那么该图柱的高和底面周长的比是( )
A.2π:1 B.1:π C.1:1 D.π:1
【考点】比的意义.
【专题】应用题;应用意识.
【答案】C
【分析】圆柱侧面展开图的一边为圆柱的底面周长,另一边为圆柱的高。
【解答】解:如果一个圆柱的侧面展开图是一个正方形,那么它的高与底面周长相等,它们的比是1:1。
故选:C。
【点评】此题主要考查圆柱的侧面展开图以及圆柱的底面半径和底面周长之间的关系,应灵活掌握,学以致用。
5.(2分)平行四边形和三角形的高相等,面积也相等,平行四边形的底是20厘米,三角形的底是( )
A.10厘米 B.20厘米 C.40厘米
【考点】三角形的周长和面积.
【专题】平面图形的认识与计算;几何直观;应用意识.
【答案】C
【分析】因为等底等高的三角形的面积是平行四边形面积的一半,所以当三角形和平行四边形的面积相等,高相等时,三角形的底是平行四边形底的2倍.据此解答.
【解答】解:20×2=40(厘米)
答:三角形的底是40厘米.
故选:C.
【点评】此题考查的目的是理解掌握等底等高的三角形和平行四边形面积之间的关系及应用.
6.(2分)有两个杯子,甲杯有100克水,乙杯有90克水.往甲杯中放25克糖,往乙杯中放20克糖,则两杯水相比较,( )
A.甲杯甜 B.乙杯甜 C.一样甜
【考点】百分率应用题.
【专题】分数百分数应用题;应用意识.
【答案】A
【分析】要求哪杯水甜,就是求哪杯水的含糖量高,用糖的重量除以糖水的总重量分别求出它们的含糖量,含糖量高的就甜.
【解答】解:甲杯的含糖量:
25÷(100+25)
=25÷125
=20%
乙杯的含糖量:
20÷(90+20)
=20÷110
≈18.2%
20%>18.2%,甲杯甜.
故选:A.
【点评】本题也可以求出糖的重量占水的几分之几,这一分率高的就甜.
二.解答题(共12小题,满分23分)
7.(4分) 12 :1580%= 32 ÷40= 0.8 (填小数)= 八成 (成数)
【考点】比与分数、除法的关系;小数、分数和百分数之间的关系及其转化;成数.
【专题】数感.
【答案】12,5,32,0.8,八成。
【分析】把80%化成分母是100的分数再化简是;根据比与分数的关系4:5,再根据比的性质,比的前、后项都乘3就是12:15;根据分数与除法的关系4÷5,再根据商不变的性质,被除数、除数都乘8就是32÷40;把80%的小数点向左移动两位同时去掉百分号就是0.8;根据成数的意义80%就是八成。
【解答】解:12:1580%=32÷40=0.8=八成
故答案为:12,5,32,0.8,八成。
【点评】此题主要是考查小数、分数、百分数、除法、比、成数之间的关系及转化。利用它们之间的关系和性质进行转化即可。
8.(2分)24千克的是 3 千克;24千克比 21 千克多。
【考点】分数除法;分数乘法.
【专题】文字题;应用意识.
【答案】3,21。
【分析】用24乘即可求出24千克的是多少千克;用24除以(1)即可求出24千克比多少千克多。
【解答】解:243(千克)
24÷(1)
=24
=21(千克)
故答案为:3,21。
【点评】此题考查了运用分数乘除法解决实际问题。
9.(2分)一个长8米、宽6米、高5米的长方体,占地面积最小是 30 平方米,这个长方体的棱长之和是 76 米,表面积是 236 平方米,体积是 240 立方米。
【考点】长方体、正方体表面积与体积计算的应用.
【专题】立体图形的认识与计算;几何直观.
【答案】30;76;236;240。
【分析】占地面积最小就是求以6米、5米为边长的长方形的面积,长方形面积=长×宽,代入数据计算即可;长方体棱长总和=(长+宽+高)×4,据此代入数据计算即可求出棱长总和;长方体表面积=(长×宽+长×高+宽×高)×2,据此代入数据计算即可求出表面积;长方体体积=长×宽×高,据此代入数据计算即可求出体积。
【解答】解:6×5=30(平方米)
(8+6+5)×4
=19×4
=76(米)
(8×6+8×5+6×5)×2
=(48+40+30)×2
=118×2
=236(平方米)
8×6×5
=48×5
=240(立方米)
答:占地面积最小是30平方米,这个长方体的棱长之和是76米,表面积是236平方米,体积是240立方米。
故答案为:30;76;236;240。
【点评】此题考查长方体棱长总和、表面积和体积计算。掌握计算公式是解答的关键。
10.(2分)一台拖拉机小时耕地公顷,这台拖拉机1小时耕地 公顷;耕地1公顷需要 小时。
【考点】分数除法应用题.
【专题】运算能力;应用意识.
【答案】,。
【分析】一台拖拉机小时耕地公顷,求这台拖拉机1小时耕地的公顷数,即求这台拖拉机的工作效率,根据“工作效率=工作量÷工作时间”即可解答;求耕地1公顷需要的时间,根据“工作时间=工作量÷工作效率”即可解答,或直接用小时除以。
【解答】解:(公顷)
1(小时)
或(小时)
答:这台拖拉机1小时耕地公顷;耕地1公顷需要小时。
故答案为:,。
【点评】此题是考查分数除法的应用。关键是工作量、工作效率、工作时间三者之间的关系。
11.(2分)某种电器原售价500元,三月初涨价10%,四月初又在三月初的基础上降价20%。现在这款电器的售价为 440 元。
【考点】百分数的实际应用.
【专题】应用题;应用意识.
【答案】440。
【分析】根据题意,先把500元看作是单位“1”,三月初涨价10%,那么三月份售价是[500×(1+10%)]元,然后把三月份售价看作是单位“1”,用三月份售价乘(1﹣20%)就是四月份的售价,据此列式计算即可。
【解答】解:500×(1+10%)×(1﹣20%)
=500×1.1×80%
=550×80%
=440(元)
答:现在这款电器的售价为440元。
故答案为:440。
【点评】解答此题的关键是找准单位“1”的量。
12.(1分)在400g盐水中,含盐80g,盐占盐水的 20 %。
【考点】百分率应用题.
【专题】运算能力;应用意识.
【答案】20。
【分析】盐占盐水的百分之几=盐的质量÷盐水的质量×100%。
【解答】解:80÷400×100%=20%
答:盐占盐水的20%。
故答案为:20。
【点评】本题主要考查了百分率应用题,求一个数占另一个数的百分之几,用除法计算。
13.(1分)2022年春节佳佳把2500元压岁钱存入银行,整存整取两年,年利率3.75%,到期时佳佳可以从银行中取出 2687.5 元。
【考点】存款利息与纳税相关问题.
【专题】应用意识.
【答案】2687.5。
【分析】根据本息和=本金+本金×利率×存期,代入数据解答即可。
【解答】解:2500+2500×2×3.75%
=2500+187.5
=2687.5(元)
答:到期时佳佳可以从银行中取出2687.5元。
故答案为:2687.5。
【点评】本题考查了存款利息相关问题,公式:本息和=本金+本金×利率×存期。
14.(2分)一本科技书有240页,张明第一天看了这本书的,第二天看了这本书的,张明两天看了 170 页,第三天应从第 171 页看起。
【考点】分数四则复合应用题.
【专题】应用意识.
【答案】170;171。
【分析】把这本科技书的总页数看作单位“1”,则两天一共看了这本书的(),用总页数数乘()即可求出张明两天看了多少页;用两天一共看的页数加上1,即可求出第三天应从第几页看起。
【解答】解:240×()
=240
=170(页)
170+1=171(页)
答:张明两天看了170页,第三天应从第171页看起。
故答案为:170;171。
【点评】解答此类问题,首先找清单位“1”,进一步理清解答思路,列式的顺序,从而较好地解答问题。
15.(2分)10克盐加入到40克水中,盐占盐水的 20 %,水与盐水的比为 4:5 。
【考点】百分数的实际应用;比的意义.
【专题】比和比例;分数百分数应用题;运算能力;应用意识.
【答案】20,4:5。
【分析】10克盐加入到40克水中,盐水的质量就是(10+40)克,求盐占盐水的百分之几,用盐的质量除以盐水的质量;根据比的意义即可写出水与盐水的比,并化成最简整数比。
【解答】解:10÷(10+40)
=10÷50
=0.2
=20%
40:(10+40)
=40:50
=4:5
答:盐占盐水的20%,水与盐水的比为4:5。
故答案为:20,4:5。
【点评】求一个数是另一个数的百分之几,用这个数除以另一个数;根据比的意义即可写出水与盐水的比。
16.(3分)学校三、四、五年级学生共100人参加植树活动,共植树566棵。已知三、四年级的人数相等,三年级学生平均每人植树4棵,四年级学生平均每人植树5棵,五年级学生平均每人植树6.5棵。三年级学生共植树 84 棵。
【考点】平均数的含义及求平均数的方法.
【专题】运算能力;应用意识.
【答案】84。
【分析】设三年级或四年级的人数为未知数,表示出五年级的人数,根据植树棵数列方程求解。
【解答】解:设三年级x的学生,那么四年级x个学生,五年级(100﹣2x)个学生;
4x+5x+6.5×(100﹣2x)=566
9x+650﹣13x=566
4x=84
x=21
21×4=84(棵)
答:三年级学生共植树84棵。
故答案为:84。
【点评】列方程求解应用题的时候,首先要合理设未知数,然后找准等量关系。
17.(1分)淘气在看一本90页的《七彩阳光》,已经看了一周,还剩27页没看。过去的一周他平均每天看 9 页。
【考点】带括号的表内除加、除减.
【专题】运算能力;应用意识.
【答案】9。
【分析】根据题意,用90页减去还剩下的页数,求出一周看的页数,然后再除以看的天数即可求解。
【解答】解:(90﹣27)÷7
=63÷7
=9(页)
答:过去的一周他平均每天看9页。
故答案为:9。
【点评】本题主要考查了整数除法的意义和实际应用,求出已经看的页数是关键。
18.(1分)甲、乙两筐西瓜共重360千克,从甲筐取出放入乙筐,两筐西瓜就一样重.原来甲筐西瓜重 220 千克,乙筐西瓜重 140 千克。
【考点】分数四则复合应用题.
【专题】分数百分数应用题;应用意识.
【答案】220;140。
【分析】根据题意,甲、乙两筐西瓜共重360千克,后来两筐西瓜就一样重,即后来甲乙两筐西瓜重量是每筐360÷2=180(千克),从甲筐取出放入乙筐,得到甲筐重量是180千克,所以甲筐原来西瓜重:220(千克),总重量﹣甲筐西瓜重量=乙筐西瓜重量,据此解答。
【解答】解:360÷2=180(千克),
原来甲筐西瓜重:220(千克),
乙筐西瓜重:360﹣220=140(千克)。
答:原来甲筐西瓜重220千克,乙筐西瓜重140千克。
故答案为:220;140。
【点评】本题考查了分数的应用,解决本题的关键是求出原来甲筐西瓜的重量。
三.计算题(共4小题,满分35分)
19.(8分)直接写出得数。
106﹣97= 0.72÷0.4=
2.5×0.6= 0.19+0.76= 0.1﹣0.01= 0.33=
【考点】分数除法;乘方;千以内加减法;小数的加法和减法;小数乘法;小数除法;分数乘法.
【专题】运算能力.
【答案】9;1.8;0.9;;1.5;0.95;0.09;0.027。
【分析】根据整数、小数、分数加减乘除法的计算方法,直接进行口算即可。
【解答】解:
106﹣97=9 0.72÷0.4=1.8 0.9
2.5×0.6=1.5 0.19+0.76=0.95 0.1﹣0.01=0.09 0.33=0.027
【点评】本题考查了简单的计算,计算时要细心,注意平时积累经验,提高计算的水平。
20.(12分)计算下面各题,能简算的要简算。
(1) (2) (3)40
(4)5136 (5)()×9×10 (6)2025
【考点】分数的四则混合运算;运算定律与简便运算.
【专题】运算能力.
【答案】(1);(2);(3)25;(4)60;(5)2;(6)2023。
【分析】(1)按照从左向右的顺序进行计算;
(2)根据乘法交换律进行计算;
(3)(5)(6)根据乘法分配律进行计算;
(4)根据乘法结合律进行计算。
【解答】解:(1)
(2)
(3)40
(40﹣1)
39
=25
(4)5136
=(51)×(36)
=6×10
=60
(5)()×9×10
9×109×10
=72﹣70
=2
(6)2025
=(2024+1)
=20241
=2023
=2023
【点评】考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
21.(9分)解方程。
70%x=5.6
【考点】百分数方程求解;分数方程求解.
【专题】运算能力.
【答案】x=8;x=60。
【分析】根据等式的基本性质,方程两边同时除以70%。
先计算出方程左边xxx,再根据等式的性质,方程两边同时除以。
【解答】解:70%x=5.6
70%x÷70%=5.6÷70%
x=8
xx=15
x=15
x15
x=60
【点评】解方程的依据是等式的性质。解答过程要注意书写格式:上、下行等号对齐;不能连等。
22.(6分)求下面立体图形的表面积和体积。
(1)
(2)
【考点】长方体和正方体的体积;长方体和正方体的表面积.
【专题】计算题;几何直观.
【答案】(1)表面积是162平方分米,体积是90立方分米;
(2)216平方米,体积是216立方米。
【分析】(1)利用长方体的表面积和体积公式结合图中数据计算即可;
(1)利用正方体的表面积和体积公式结合图中数据计算即可。
【解答】解:(1)(15×3+15×2+3×2)×2
=81×2
=162(平方分米)
15×3×2=90(立方分米)
答:图形的表面积是162平方分米,体积是90立方分米。
(2)6×6×6=216(平方米)
6×6×6=216(立方米)
答:图形的表面积是216平方米,体积是216立方米。
【点评】本题考查的是长方体、正方体的表面积、体积公式的应用。
四.解答题(共2小题,满分6分)
23.(2分)看图列式计算。
(1)
(2)
【考点】分数除法应用题.
【专题】应用题;应用意识.
【答案】(1)98公顷;(2)735吨。
【分析】(1)把总面积看作单位“1”,用56公顷除以即可。
(2)把小麦的质量看作单位“1”,用小麦的质量除以(1)即可。
【解答】解:(1)5698(公顷)
(2)588÷(1)
=588
=735(吨)
【点评】本题考查了分数除法应用题,关键是确定单位“1”,找到具体数量对应的分率;解答依据是:已知一个数的几分之几是多少,求这个数用除法计算。
24.(4分)请你在方格(边长1厘米)纸中画一个周长是32厘米,长和宽的比是5:3的长方形。
【考点】比的应用;画指定周长的长方形、正方形.
【专题】作图题;应用意识.
【答案】
【分析】用周长÷2,先求出一组长和宽的和,已知长和宽的比,按照比例分配,即可求出长和宽,画图即可。
【解答】解:32÷2=16(厘米)
长:1610(厘米)
宽:166(厘米)
如下图所示:
【点评】本题考查按比例分配,先求出长方形的长与宽是解题的关键,注意周长除以2。
五.解答题(共6小题,满分24分)
25.(5分)一个长方体文具盒,底面积是200cm2,高是3cm,这个文具盒的体积是多少立方厘米?合多少立方分米?
【考点】长方体和正方体的体积.
【专题】应用题;立体图形的认识与计算.
【答案】见试题解答内容
【分析】根据长方体的体积公式:V=Sh,把数据代入公式解答即可求出这个文具盒的体积,然后转化单位即可.
【解答】解:200×3=600(立方厘米)
600立方厘米=0.6立方分米
答:这个文具盒的体积是600立方厘米,合0.6立方分米.
【点评】此题主要考查长方体的体积(容积)公式V=Sh的灵活运用.
26.(4分)学校图书室今年有图书2760册,比去年图书数量增加了15%。学校图书室去年有图书多少册?
【考点】百分数的实际应用.
【专题】应用题;应用意识.
【答案】2400册。
【分析】把去年图书的数量看作单位“1”,则今年的是(1+15%),根据已知一个数的百分之几是多少,求这个数用除法计算即可。
【解答】解:2760÷(1+15%)
=2760÷1.15
=2400(册)
答:学校图书室去年有图书2400册。
【点评】本题考查的是百分数除法意义的运用。
27.(4分)某电脑商店四周卖出一批电脑,第一周卖出总台数的,第二周卖出总台数的,第三周与第四周卖出的台数比是5:2,已知第四周比第三周少卖出了180台,第三周和第四周一共卖出了多少台?这批电脑原有多少台?
【考点】分数四则复合应用题.
【专题】应用题;应用意识.
【答案】420台,640台。
【分析】已知第三周与第四周卖出台数的比是5:2,可以看作第三周卖出的占5份,第四周卖出的占2份,相差3份,用180除以3求出每份是多少,再乘(5+2)求出第三周和第四周一共卖出的台数。把这批电脑看作单位“1”,减去第一周和第二周卖出的分率,正好与第三周和第四周共卖出的台数相对应,用除法求出这批电脑的总台数。据此解答。
【解答】解:180÷(5﹣2)×(5+2)
=60×7
=420(台)
420÷(1)
=420
=640(台)
答:第三周和第四周一共卖出了420台。这批电脑原有640台。
【点评】解答本题的关键是找出与第三周和第四周卖出台数相对应的分率,进而求出总数。
28.(4分)笑笑读一本故事书,已读页数是全书的,如果再读14页,这时已读页数和全书的页数之比是3:8,这本书共有多少页?
【考点】比的应用.
【专题】运算能力;应用意识.
【答案】112页。
【分析】把这本书的页数看作单位“1”,已读页数是全书的,如果再读14页,已读的页数就占全书的,则14页占全书的(),根据分数除法的意义,用14页除以(),就是这本书的页数。
【解答】解:14÷()
=14
=112(页)
答:这本书共有112页。
【点评】解答此题的关键是把比转化成分数,然后再根据分数除法的意义解答。
29.(4分)某校语文老师、科学老师、音乐老师的人数比是15:3:2,如果该校音乐老师有6人,那么语文老师和科学老师各有多少人?
【考点】比的应用.
【专题】比和比例应用题;应用意识.
【答案】45人;9人。
【分析】根据题意可得音乐老师人数占语文老师、科学老师、音乐老师总人数的分率:2÷(15+3+2),三科总人数=音乐老师人数÷音乐老师占三科总人数的分率,据此求出三科总人数,再用三科总人数分别乘语文老师人数和科学老师人数占总人数的百分率,即可求出语文老师和科学老师各有多少人。
【解答】解:2÷(15+3+2)
=2÷20
660(人)
60
=60
=45(人)
60
=60
=9(人)
答:语文老师有45人,科学老师有9人。
【点评】此题考查比的应用。
30.(3分)有一块边长2米的正方形铁板,把它锯成一个最大的圆,面积会比原来减少百分之几?
【考点】百分数的实际应用.
【专题】应用题;应用意识.
【答案】21.5%。
【分析】由题意知,在正方形内锯成面积最大的圆,其直径就等于正方形的边长,即2米;可利用圆的面积=圆周率×半径的平方,求出圆的面积,则减少的面积就等于正方形的面积与圆的面积之差,然后再用这个差除以正方形的面积,即可求出减少的百分数。
【解答】解:2×2﹣3.14×(2÷2)2
=4﹣3.14
=0.86(平方米)
0.86÷(2×2)
=0.86÷4
=21.5%
答:面积会比原来减少了21.5%。
【点评】解答此题要明确:在正方形内锯成面积最大的圆,其直径就等于正方形的边长。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
江苏省南京市2025-2026学年六年级上学期期末模拟数学预测卷
一.选择题(共6小题,满分12分,每小题2分)
1.(2分)下列( )个图形能折成正方体.
A. B. C.
2.(2分)下面与:的比值相等的比是( )
A.0.5:0.4 B.5:4 C.20:25
3.(2分)20cm增加后是( )cm。
A. B.24 C.25 D.30
4.(2分)如果一个圆柱的侧面展开图是一个正方形,那么该图柱的高和底面周长的比是( )
A.2π:1 B.1:π C.1:1 D.π:1
5.(2分)平行四边形和三角形的高相等,面积也相等,平行四边形的底是20厘米,三角形的底是( )
A.10厘米 B.20厘米 C.40厘米
6.(2分)有两个杯子,甲杯有100克水,乙杯有90克水.往甲杯中放25克糖,往乙杯中放20克糖,则两杯水相比较,( )
A.甲杯甜 B.乙杯甜 C.一样甜
二.解答题(共12小题,满分23分)
7.(4分) :1580%= ÷40= (填小数)= (成数)
8.(2分)24千克的是 千克;24千克比 千克多。
9.(2分)一个长8米、宽6米、高5米的长方体,占地面积最小是 平方米,这个长方体的棱长之和是 米,表面积是 平方米,体积是 立方米。
10.(2分)一台拖拉机小时耕地公顷,这台拖拉机1小时耕地 公顷;耕地1公顷需要 小时。
11.(2分)某种电器原售价500元,三月初涨价10%,四月初又在三月初的基础上降价20%。现在这款电器的售价为 元。
12.(1分)在400g盐水中,含盐80g,盐占盐水的 %。
13.(1分)2022年春节佳佳把2500元压岁钱存入银行,整存整取两年,年利率3.75%,到期时佳佳可以从银行中取出 元。
14.(2分)一本科技书有240页,张明第一天看了这本书的,第二天看了这本书的,张明两天看了 页,第三天应从第 页看起。
15.(2分)10克盐加入到40克水中,盐占盐水的 %,水与盐水的比为 。
16.(3分)学校三、四、五年级学生共100人参加植树活动,共植树566棵。已知三、四年级的人数相等,三年级学生平均每人植树4棵,四年级学生平均每人植树5棵,五年级学生平均每人植树6.5棵。三年级学生共植树 棵。
17.(1分)淘气在看一本90页的《七彩阳光》,已经看了一周,还剩27页没看。过去的一周他平均每天看 页。
18.(1分)甲、乙两筐西瓜共重360千克,从甲筐取出放入乙筐,两筐西瓜就一样重.原来甲筐西瓜重 千克,乙筐西瓜重 千克。
三.计算题(共4小题,满分35分)
19.(8分)直接写出得数。
106﹣97= 0.72÷0.4=
2.5×0.6= 0.19+0.76= 0.1﹣0.01= 0.33=
20.(12分)计算下面各题,能简算的要简算。
(1) (2) (3)40
(4)5136 (5)()×9×10 (6)2025
21.(9分)解方程。
70%x=5.6
22.(6分)求下面立体图形的表面积和体积。
(1) (2)
四.解答题(共2小题,满分6分)
23.(2分)看图列式计算。
(1)
24.(4分)请你在方格(边长1厘米)纸中画一个周长是32厘米,长和宽的比是5:3的长方形。
五.解答题(共6小题,满分24分)
25.(5分)一个长方体文具盒,底面积是200cm2,高是3cm,这个文具盒的体积是多少立方厘米?合多少立方分米?
26.(4分)学校图书室今年有图书2760册,比去年图书数量增加了15%。学校图书室去年有图书多少册?
27.(4分)某电脑商店四周卖出一批电脑,第一周卖出总台数的,第二周卖出总台数的,第三周与第四周卖出的台数比是5:2,已知第四周比第三周少卖出了180台,第三周和第四周一共卖出了多少台?这批电脑原有多少台?
28.(4分)笑笑读一本故事书,已读页数是全书的,如果再读14页,这时已读页数和全书的页数之比是3:8,这本书共有多少页?
29.(4分)某校语文老师、科学老师、音乐老师的人数比是15:3:2,如果该校音乐老师有6人,那么语文老师和科学老师各有多少人?
30.(3分)有一块边长2米的正方形铁板,把它锯成一个最大的圆,面积会比原来减少百分之几?
参考答案与试题解析
一.选择题(共6小题,满分12分,每小题2分)
1.(2分)下列( )个图形能折成正方体.
A. B. C.
【考点】正方体的展开图.
【专题】作图题;图形与变换.
【答案】B
【分析】根据正方体展开图的11种特征,选项A和选项C不属于正方体展开图,不能折成正方体;选项B属于正方体展开图的“1﹣4﹣1”型,能折成正方体.
【解答】解:根据正方体展开图的特征,选项A和选项C不能折成正方体;选项B能折成正方体.
故选:B.
【点评】正方体展开图有11种特征,分四种类型,即:第一种:“1﹣4﹣1”结构,即第一行放1个,第二行放4个,第三行放1个;第二种:“2﹣2﹣2”结构,即每一行放2个正方形,此种结构只有一种展开图;第三种:“3﹣3”结构,即每一行放3个正方形,只有一种展开图;第四种:“1﹣3﹣2”结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形.
2.(2分)下面与:的比值相等的比是( )
A.0.5:0.4 B.5:4 C.20:25
【考点】求比值和化简比.
【专题】比和比例;运算能力.
【答案】C
【分析】先用比:的前项除以后项,得出比值,再用同样的方法求出每一个选项中比的比值,进而找出与:的比值相等的比得解.
【解答】解::
A、0.5:0.4=0.5÷0.4,因为,所以不符合题意
B、5:4=5÷4,因为,所以不符合题意
C、20:25=20÷25,因为,所以符合题意.
故选:C.
【点评】此题考查学生求比值的方法的运用.
3.(2分)20cm增加后是( )cm。
A. B.24 C.25 D.30
【考点】分数乘法.
【专题】应用意识.
【答案】B
【分析】将20厘米看作单位“1”,用20厘米乘(1),即可求出20厘米增加后是多少厘米,据此解答。
【解答】解:20×(1)
=20
=24(cm)
答:20cm增加后是24cm。
故选:B。
【点评】求比一个数多这个数的几分之几是多少,用乘加混合运算解答。
4.(2分)如果一个圆柱的侧面展开图是一个正方形,那么该图柱的高和底面周长的比是( )
A.2π:1 B.1:π C.1:1 D.π:1
【考点】比的意义.
【专题】应用题;应用意识.
【答案】C
【分析】圆柱侧面展开图的一边为圆柱的底面周长,另一边为圆柱的高。
【解答】解:如果一个圆柱的侧面展开图是一个正方形,那么它的高与底面周长相等,它们的比是1:1。
故选:C。
【点评】此题主要考查圆柱的侧面展开图以及圆柱的底面半径和底面周长之间的关系,应灵活掌握,学以致用。
5.(2分)平行四边形和三角形的高相等,面积也相等,平行四边形的底是20厘米,三角形的底是( )
A.10厘米 B.20厘米 C.40厘米
【考点】三角形的周长和面积.
【专题】平面图形的认识与计算;几何直观;应用意识.
【答案】C
【分析】因为等底等高的三角形的面积是平行四边形面积的一半,所以当三角形和平行四边形的面积相等,高相等时,三角形的底是平行四边形底的2倍.据此解答.
【解答】解:20×2=40(厘米)
答:三角形的底是40厘米.
故选:C.
【点评】此题考查的目的是理解掌握等底等高的三角形和平行四边形面积之间的关系及应用.
6.(2分)有两个杯子,甲杯有100克水,乙杯有90克水.往甲杯中放25克糖,往乙杯中放20克糖,则两杯水相比较,( )
A.甲杯甜 B.乙杯甜 C.一样甜
【考点】百分率应用题.
【专题】分数百分数应用题;应用意识.
【答案】A
【分析】要求哪杯水甜,就是求哪杯水的含糖量高,用糖的重量除以糖水的总重量分别求出它们的含糖量,含糖量高的就甜.
【解答】解:甲杯的含糖量:
25÷(100+25)
=25÷125
=20%
乙杯的含糖量:
20÷(90+20)
=20÷110
≈18.2%
20%>18.2%,甲杯甜.
故选:A.
【点评】本题也可以求出糖的重量占水的几分之几,这一分率高的就甜.
二.解答题(共12小题,满分23分)
7.(4分) 12 :1580%= 32 ÷40= 0.8 (填小数)= 八成 (成数)
【考点】比与分数、除法的关系;小数、分数和百分数之间的关系及其转化;成数.
【专题】数感.
【答案】12,5,32,0.8,八成。
【分析】把80%化成分母是100的分数再化简是;根据比与分数的关系4:5,再根据比的性质,比的前、后项都乘3就是12:15;根据分数与除法的关系4÷5,再根据商不变的性质,被除数、除数都乘8就是32÷40;把80%的小数点向左移动两位同时去掉百分号就是0.8;根据成数的意义80%就是八成。
【解答】解:12:1580%=32÷40=0.8=八成
故答案为:12,5,32,0.8,八成。
【点评】此题主要是考查小数、分数、百分数、除法、比、成数之间的关系及转化。利用它们之间的关系和性质进行转化即可。
8.(2分)24千克的是 3 千克;24千克比 21 千克多。
【考点】分数除法;分数乘法.
【专题】文字题;应用意识.
【答案】3,21。
【分析】用24乘即可求出24千克的是多少千克;用24除以(1)即可求出24千克比多少千克多。
【解答】解:243(千克)
24÷(1)
=24
=21(千克)
故答案为:3,21。
【点评】此题考查了运用分数乘除法解决实际问题。
9.(2分)一个长8米、宽6米、高5米的长方体,占地面积最小是 30 平方米,这个长方体的棱长之和是 76 米,表面积是 236 平方米,体积是 240 立方米。
【考点】长方体、正方体表面积与体积计算的应用.
【专题】立体图形的认识与计算;几何直观.
【答案】30;76;236;240。
【分析】占地面积最小就是求以6米、5米为边长的长方形的面积,长方形面积=长×宽,代入数据计算即可;长方体棱长总和=(长+宽+高)×4,据此代入数据计算即可求出棱长总和;长方体表面积=(长×宽+长×高+宽×高)×2,据此代入数据计算即可求出表面积;长方体体积=长×宽×高,据此代入数据计算即可求出体积。
【解答】解:6×5=30(平方米)
(8+6+5)×4
=19×4
=76(米)
(8×6+8×5+6×5)×2
=(48+40+30)×2
=118×2
=236(平方米)
8×6×5
=48×5
=240(立方米)
答:占地面积最小是30平方米,这个长方体的棱长之和是76米,表面积是236平方米,体积是240立方米。
故答案为:30;76;236;240。
【点评】此题考查长方体棱长总和、表面积和体积计算。掌握计算公式是解答的关键。
10.(2分)一台拖拉机小时耕地公顷,这台拖拉机1小时耕地 公顷;耕地1公顷需要 小时。
【考点】分数除法应用题.
【专题】运算能力;应用意识.
【答案】,。
【分析】一台拖拉机小时耕地公顷,求这台拖拉机1小时耕地的公顷数,即求这台拖拉机的工作效率,根据“工作效率=工作量÷工作时间”即可解答;求耕地1公顷需要的时间,根据“工作时间=工作量÷工作效率”即可解答,或直接用小时除以。
【解答】解:(公顷)
1(小时)
或(小时)
答:这台拖拉机1小时耕地公顷;耕地1公顷需要小时。
故答案为:,。
【点评】此题是考查分数除法的应用。关键是工作量、工作效率、工作时间三者之间的关系。
11.(2分)某种电器原售价500元,三月初涨价10%,四月初又在三月初的基础上降价20%。现在这款电器的售价为 440 元。
【考点】百分数的实际应用.
【专题】应用题;应用意识.
【答案】440。
【分析】根据题意,先把500元看作是单位“1”,三月初涨价10%,那么三月份售价是[500×(1+10%)]元,然后把三月份售价看作是单位“1”,用三月份售价乘(1﹣20%)就是四月份的售价,据此列式计算即可。
【解答】解:500×(1+10%)×(1﹣20%)
=500×1.1×80%
=550×80%
=440(元)
答:现在这款电器的售价为440元。
故答案为:440。
【点评】解答此题的关键是找准单位“1”的量。
12.(1分)在400g盐水中,含盐80g,盐占盐水的 20 %。
【考点】百分率应用题.
【专题】运算能力;应用意识.
【答案】20。
【分析】盐占盐水的百分之几=盐的质量÷盐水的质量×100%。
【解答】解:80÷400×100%=20%
答:盐占盐水的20%。
故答案为:20。
【点评】本题主要考查了百分率应用题,求一个数占另一个数的百分之几,用除法计算。
13.(1分)2022年春节佳佳把2500元压岁钱存入银行,整存整取两年,年利率3.75%,到期时佳佳可以从银行中取出 2687.5 元。
【考点】存款利息与纳税相关问题.
【专题】应用意识.
【答案】2687.5。
【分析】根据本息和=本金+本金×利率×存期,代入数据解答即可。
【解答】解:2500+2500×2×3.75%
=2500+187.5
=2687.5(元)
答:到期时佳佳可以从银行中取出2687.5元。
故答案为:2687.5。
【点评】本题考查了存款利息相关问题,公式:本息和=本金+本金×利率×存期。
14.(2分)一本科技书有240页,张明第一天看了这本书的,第二天看了这本书的,张明两天看了 170 页,第三天应从第 171 页看起。
【考点】分数四则复合应用题.
【专题】应用意识.
【答案】170;171。
【分析】把这本科技书的总页数看作单位“1”,则两天一共看了这本书的(),用总页数数乘()即可求出张明两天看了多少页;用两天一共看的页数加上1,即可求出第三天应从第几页看起。
【解答】解:240×()
=240
=170(页)
170+1=171(页)
答:张明两天看了170页,第三天应从第171页看起。
故答案为:170;171。
【点评】解答此类问题,首先找清单位“1”,进一步理清解答思路,列式的顺序,从而较好地解答问题。
15.(2分)10克盐加入到40克水中,盐占盐水的 20 %,水与盐水的比为 4:5 。
【考点】百分数的实际应用;比的意义.
【专题】比和比例;分数百分数应用题;运算能力;应用意识.
【答案】20,4:5。
【分析】10克盐加入到40克水中,盐水的质量就是(10+40)克,求盐占盐水的百分之几,用盐的质量除以盐水的质量;根据比的意义即可写出水与盐水的比,并化成最简整数比。
【解答】解:10÷(10+40)
=10÷50
=0.2
=20%
40:(10+40)
=40:50
=4:5
答:盐占盐水的20%,水与盐水的比为4:5。
故答案为:20,4:5。
【点评】求一个数是另一个数的百分之几,用这个数除以另一个数;根据比的意义即可写出水与盐水的比。
16.(3分)学校三、四、五年级学生共100人参加植树活动,共植树566棵。已知三、四年级的人数相等,三年级学生平均每人植树4棵,四年级学生平均每人植树5棵,五年级学生平均每人植树6.5棵。三年级学生共植树 84 棵。
【考点】平均数的含义及求平均数的方法.
【专题】运算能力;应用意识.
【答案】84。
【分析】设三年级或四年级的人数为未知数,表示出五年级的人数,根据植树棵数列方程求解。
【解答】解:设三年级x的学生,那么四年级x个学生,五年级(100﹣2x)个学生;
4x+5x+6.5×(100﹣2x)=566
9x+650﹣13x=566
4x=84
x=21
21×4=84(棵)
答:三年级学生共植树84棵。
故答案为:84。
【点评】列方程求解应用题的时候,首先要合理设未知数,然后找准等量关系。
17.(1分)淘气在看一本90页的《七彩阳光》,已经看了一周,还剩27页没看。过去的一周他平均每天看 9 页。
【考点】带括号的表内除加、除减.
【专题】运算能力;应用意识.
【答案】9。
【分析】根据题意,用90页减去还剩下的页数,求出一周看的页数,然后再除以看的天数即可求解。
【解答】解:(90﹣27)÷7
=63÷7
=9(页)
答:过去的一周他平均每天看9页。
故答案为:9。
【点评】本题主要考查了整数除法的意义和实际应用,求出已经看的页数是关键。
18.(1分)甲、乙两筐西瓜共重360千克,从甲筐取出放入乙筐,两筐西瓜就一样重.原来甲筐西瓜重 220 千克,乙筐西瓜重 140 千克。
【考点】分数四则复合应用题.
【专题】分数百分数应用题;应用意识.
【答案】220;140。
【分析】根据题意,甲、乙两筐西瓜共重360千克,后来两筐西瓜就一样重,即后来甲乙两筐西瓜重量是每筐360÷2=180(千克),从甲筐取出放入乙筐,得到甲筐重量是180千克,所以甲筐原来西瓜重:220(千克),总重量﹣甲筐西瓜重量=乙筐西瓜重量,据此解答。
【解答】解:360÷2=180(千克),
原来甲筐西瓜重:220(千克),
乙筐西瓜重:360﹣220=140(千克)。
答:原来甲筐西瓜重220千克,乙筐西瓜重140千克。
故答案为:220;140。
【点评】本题考查了分数的应用,解决本题的关键是求出原来甲筐西瓜的重量。
三.计算题(共4小题,满分35分)
19.(8分)直接写出得数。
106﹣97= 0.72÷0.4=
2.5×0.6= 0.19+0.76= 0.1﹣0.01= 0.33=
【考点】分数除法;乘方;千以内加减法;小数的加法和减法;小数乘法;小数除法;分数乘法.
【专题】运算能力.
【答案】9;1.8;0.9;;1.5;0.95;0.09;0.027。
【分析】根据整数、小数、分数加减乘除法的计算方法,直接进行口算即可。
【解答】解:
106﹣97=9 0.72÷0.4=1.8 0.9
2.5×0.6=1.5 0.19+0.76=0.95 0.1﹣0.01=0.09 0.33=0.027
【点评】本题考查了简单的计算,计算时要细心,注意平时积累经验,提高计算的水平。
20.(12分)计算下面各题,能简算的要简算。
(1) (2) (3)40
(4)5136 (5)()×9×10 (6)2025
【考点】分数的四则混合运算;运算定律与简便运算.
【专题】运算能力.
【答案】(1);(2);(3)25;(4)60;(5)2;(6)2023。
【分析】(1)按照从左向右的顺序进行计算;
(2)根据乘法交换律进行计算;
(3)(5)(6)根据乘法分配律进行计算;
(4)根据乘法结合律进行计算。
【解答】解:(1)
(2)
(3)40
(40﹣1)
39
=25
(4)5136
=(51)×(36)
=6×10
=60
(5)()×9×10
9×109×10
=72﹣70
=2
(6)2025
=(2024+1)
=20241
=2023
=2023
【点评】考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
21.(9分)解方程。
70%x=5.6
【考点】百分数方程求解;分数方程求解.
【专题】运算能力.
【答案】x=8;x=60。
【分析】根据等式的基本性质,方程两边同时除以70%。
先计算出方程左边xxx,再根据等式的性质,方程两边同时除以。
【解答】解:70%x=5.6
70%x÷70%=5.6÷70%
x=8
xx=15
x=15
x15
x=60
【点评】解方程的依据是等式的性质。解答过程要注意书写格式:上、下行等号对齐;不能连等。
22.(6分)求下面立体图形的表面积和体积。
(1)
(2)
【考点】长方体和正方体的体积;长方体和正方体的表面积.
【专题】计算题;几何直观.
【答案】(1)表面积是162平方分米,体积是90立方分米;
(2)216平方米,体积是216立方米。
【分析】(1)利用长方体的表面积和体积公式结合图中数据计算即可;
(1)利用正方体的表面积和体积公式结合图中数据计算即可。
【解答】解:(1)(15×3+15×2+3×2)×2
=81×2
=162(平方分米)
15×3×2=90(立方分米)
答:图形的表面积是162平方分米,体积是90立方分米。
(2)6×6×6=216(平方米)
6×6×6=216(立方米)
答:图形的表面积是216平方米,体积是216立方米。
【点评】本题考查的是长方体、正方体的表面积、体积公式的应用。
四.解答题(共2小题,满分6分)
23.(2分)看图列式计算。
(1)
(2)
【考点】分数除法应用题.
【专题】应用题;应用意识.
【答案】(1)98公顷;(2)735吨。
【分析】(1)把总面积看作单位“1”,用56公顷除以即可。
(2)把小麦的质量看作单位“1”,用小麦的质量除以(1)即可。
【解答】解:(1)5698(公顷)
(2)588÷(1)
=588
=735(吨)
【点评】本题考查了分数除法应用题,关键是确定单位“1”,找到具体数量对应的分率;解答依据是:已知一个数的几分之几是多少,求这个数用除法计算。
24.(4分)请你在方格(边长1厘米)纸中画一个周长是32厘米,长和宽的比是5:3的长方形。
【考点】比的应用;画指定周长的长方形、正方形.
【专题】作图题;应用意识.
【答案】
【分析】用周长÷2,先求出一组长和宽的和,已知长和宽的比,按照比例分配,即可求出长和宽,画图即可。
【解答】解:32÷2=16(厘米)
长:1610(厘米)
宽:166(厘米)
如下图所示:
【点评】本题考查按比例分配,先求出长方形的长与宽是解题的关键,注意周长除以2。
五.解答题(共6小题,满分24分)
25.(5分)一个长方体文具盒,底面积是200cm2,高是3cm,这个文具盒的体积是多少立方厘米?合多少立方分米?
【考点】长方体和正方体的体积.
【专题】应用题;立体图形的认识与计算.
【答案】见试题解答内容
【分析】根据长方体的体积公式:V=Sh,把数据代入公式解答即可求出这个文具盒的体积,然后转化单位即可.
【解答】解:200×3=600(立方厘米)
600立方厘米=0.6立方分米
答:这个文具盒的体积是600立方厘米,合0.6立方分米.
【点评】此题主要考查长方体的体积(容积)公式V=Sh的灵活运用.
26.(4分)学校图书室今年有图书2760册,比去年图书数量增加了15%。学校图书室去年有图书多少册?
【考点】百分数的实际应用.
【专题】应用题;应用意识.
【答案】2400册。
【分析】把去年图书的数量看作单位“1”,则今年的是(1+15%),根据已知一个数的百分之几是多少,求这个数用除法计算即可。
【解答】解:2760÷(1+15%)
=2760÷1.15
=2400(册)
答:学校图书室去年有图书2400册。
【点评】本题考查的是百分数除法意义的运用。
27.(4分)某电脑商店四周卖出一批电脑,第一周卖出总台数的,第二周卖出总台数的,第三周与第四周卖出的台数比是5:2,已知第四周比第三周少卖出了180台,第三周和第四周一共卖出了多少台?这批电脑原有多少台?
【考点】分数四则复合应用题.
【专题】应用题;应用意识.
【答案】420台,640台。
【分析】已知第三周与第四周卖出台数的比是5:2,可以看作第三周卖出的占5份,第四周卖出的占2份,相差3份,用180除以3求出每份是多少,再乘(5+2)求出第三周和第四周一共卖出的台数。把这批电脑看作单位“1”,减去第一周和第二周卖出的分率,正好与第三周和第四周共卖出的台数相对应,用除法求出这批电脑的总台数。据此解答。
【解答】解:180÷(5﹣2)×(5+2)
=60×7
=420(台)
420÷(1)
=420
=640(台)
答:第三周和第四周一共卖出了420台。这批电脑原有640台。
【点评】解答本题的关键是找出与第三周和第四周卖出台数相对应的分率,进而求出总数。
28.(4分)笑笑读一本故事书,已读页数是全书的,如果再读14页,这时已读页数和全书的页数之比是3:8,这本书共有多少页?
【考点】比的应用.
【专题】运算能力;应用意识.
【答案】112页。
【分析】把这本书的页数看作单位“1”,已读页数是全书的,如果再读14页,已读的页数就占全书的,则14页占全书的(),根据分数除法的意义,用14页除以(),就是这本书的页数。
【解答】解:14÷()
=14
=112(页)
答:这本书共有112页。
【点评】解答此题的关键是把比转化成分数,然后再根据分数除法的意义解答。
29.(4分)某校语文老师、科学老师、音乐老师的人数比是15:3:2,如果该校音乐老师有6人,那么语文老师和科学老师各有多少人?
【考点】比的应用.
【专题】比和比例应用题;应用意识.
【答案】45人;9人。
【分析】根据题意可得音乐老师人数占语文老师、科学老师、音乐老师总人数的分率:2÷(15+3+2),三科总人数=音乐老师人数÷音乐老师占三科总人数的分率,据此求出三科总人数,再用三科总人数分别乘语文老师人数和科学老师人数占总人数的百分率,即可求出语文老师和科学老师各有多少人。
【解答】解:2÷(15+3+2)
=2÷20
660(人)
60
=60
=45(人)
60
=60
=9(人)
答:语文老师有45人,科学老师有9人。
【点评】此题考查比的应用。
30.(3分)有一块边长2米的正方形铁板,把它锯成一个最大的圆,面积会比原来减少百分之几?
【考点】百分数的实际应用.
【专题】应用题;应用意识.
【答案】21.5%。
【分析】由题意知,在正方形内锯成面积最大的圆,其直径就等于正方形的边长,即2米;可利用圆的面积=圆周率×半径的平方,求出圆的面积,则减少的面积就等于正方形的面积与圆的面积之差,然后再用这个差除以正方形的面积,即可求出减少的百分数。
【解答】解:2×2﹣3.14×(2÷2)2
=4﹣3.14
=0.86(平方米)
0.86÷(2×2)
=0.86÷4
=21.5%
答:面积会比原来减少了21.5%。
【点评】解答此题要明确:在正方形内锯成面积最大的圆,其直径就等于正方形的边长。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
