【期末押题卷】安徽省合肥市2025-2026学年五年级上学期期末模拟数学预测卷苏教版(含解析)
文档属性
| 名称 | 【期末押题卷】安徽省合肥市2025-2026学年五年级上学期期末模拟数学预测卷苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 22:26:47 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
安徽省合肥市2025-2026学年五年级上学期期末模拟数学预测卷
一.填空题(共10小题,满分18分)
1.(2分)8个2.4是 ,2.4中有8个 。
2.(2分)若A×B=45,则(A×3)×B= ,(A×2)×(B×5)= 。若A÷B=5……2,则(A×10)÷(B×10)= …… 。
3.(2分)快快和乐乐在同一个班,乐乐的座位在第2列第5行,记作 ;快快的位置在第5列第4行,记作 。
4.(1分)□+□=□×□(□表示同一个数)□= .
5.(3分)不计算,直接写出下面各题的积或商。
(1)
(2)
6.(1分)每千克苹果a元,每千克香蕉b元,买5千克苹果要 元,买7千克香蕉要 元,买这两种水果一共花了 元.
7.(2分)0.363636……的循环节是 ,用简便方法记作 ,保留三位小数是 。
8.(2分)一个三角形的底是6米,高是4米,它的面积是 平方米.
9.(2分)如图所示的转盘停止转动后,指针最可能停在第 区域.指针停在奇数区域的可能性比停在偶数区域的可能性要 .
10.(1分)观察前三个算式,找规律完成后面的算式。
143×63=9009
143×56=8008
143×49=7007
143×35=
143× =3003
二.选择题(共10小题,满分20分,每小题2分)
11.(2分)某小学共有9个社团,人数最多的社团是42人,人数最少的社团是29人。对这所学校参加社团的总人数进行估计,结果正确的是( )
A.一定小于270人
B.一定大于400人
C.大于200人且小于400人
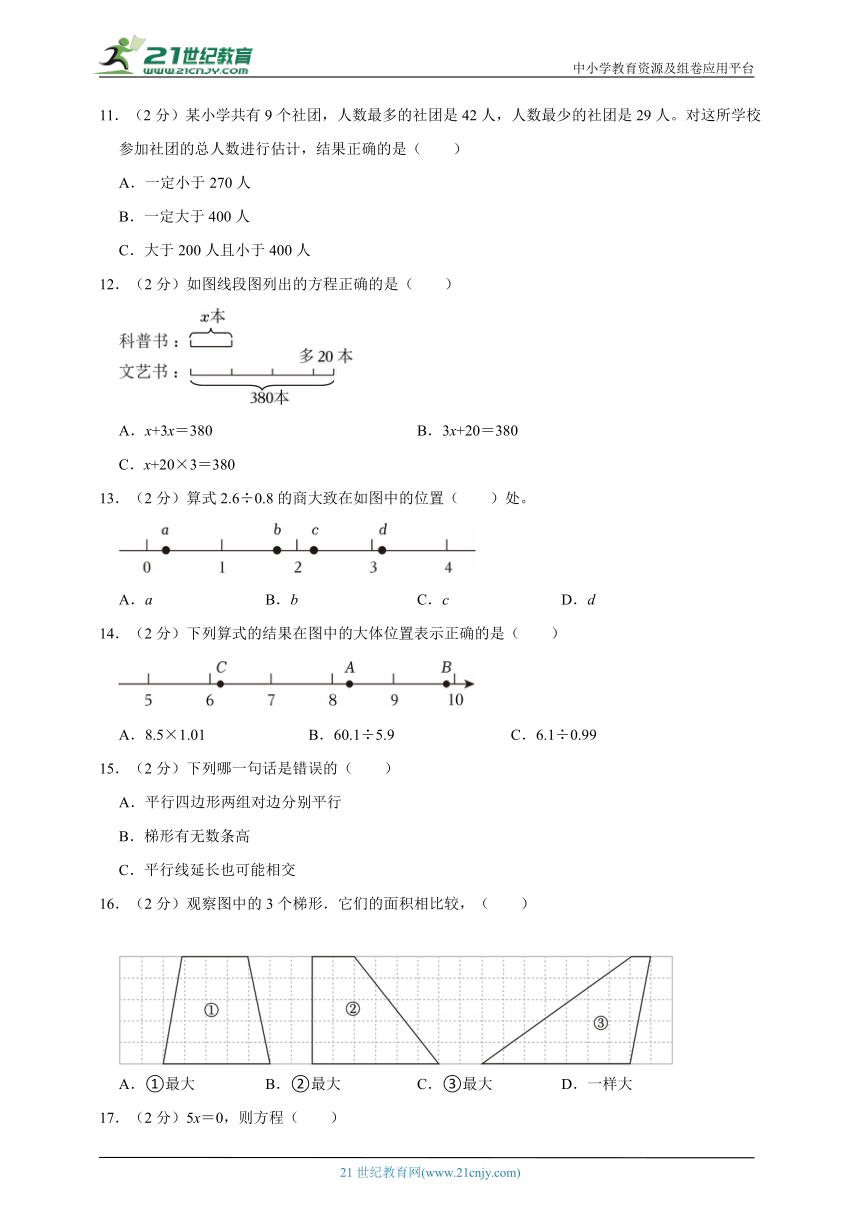
12.(2分)如图线段图列出的方程正确的是( )
A.x+3x=380 B.3x+20=380
C.x+20×3=380
13.(2分)算式2.6÷0.8的商大致在如图中的位置( )处。
A.a B.b C.c D.d
14.(2分)下列算式的结果在图中的大体位置表示正确的是( )
A.8.5×1.01 B.60.1÷5.9 C.6.1÷0.99
15.(2分)下列哪一句话是错误的( )
A.平行四边形两组对边分别平行
B.梯形有无数条高
C.平行线延长也可能相交
16.(2分)观察图中的3个梯形.它们的面积相比较,( )
A.①最大 B.②最大 C.③最大 D.一样大
17.(2分)5x=0,则方程( )
A.没有解 B.有无数个解
C.只有一个解
18.(2分)有7名同学围坐一圈,张老师有75张卡片,她依次每人每次发一张,直到发完为止,得到多于10张卡片的学生有( )人。
A.5 B.6 C.10
19.(2分)一个平行四边形的底不变,高扩大到原来的4倍,它的面积( )
A.不变 B.扩大到原来的2倍
C.扩大到原来的4倍 D.缩小到原来的
20.(2分)在一条长300米的公路两边种树,每隔3米种一棵。两端都种,一共种( )棵。
A.100 B.101 C.201 D.202
三.计算题(共4小题,满分33分)
21.(8分)列竖式计算下面各题,带*的要写出验算过程。
32.4×13= 20.5×2.6= *1.28×0.35=
27÷36= *9.01÷17= 0.76×1.4≈(结果保留两位小数)
22.(7分)用竖式计算。
1.09×2.3
0.468÷0.65
23.(12分)用简便方法计算。
(1)101×24﹣24 (2)6100÷25÷4 (3)23×46+23×54
24.(6分)解方程。
3×(x+2.1)=10.5
(x﹣3)÷2=7.5
四.操作题(共1小题,满分5分,每小题5分)
25.(5分)三角形ABC的顶点在左边方格中的位置是A(3,6),B(1,2),C(3,0)。
(1)请在方格中画出三角形ABC,并画出三角形ABC向右平移3格后的图形。
(2)在方格中画一个和三角形ABC面积相等的平行四边形。
(3)在方格中画一个梯形,要求面积是三角形ABC的2倍。
五.应用题(共5小题,满分24分)
26.(3分)学校共有620名同学参加大课间录像活动,如果要站成32列,平均每列多少名同学?还剩多少名同学?
27.(4分)加工一批零件,李师傅单独做,需要15天:赵师傅单独做,需要10天。两位师傅合作,多少天能完成任务?
28.(5分)一块近似于平行四边形的草坪,中间有一条1米宽的石子路(如图)。如果铺1平方米的草坪需要18元,铺好这块草坪一共需要多少元?
29.(5分)如图,阴影部分表示铺设人造草坪的区域。人造草坪的面积是多少平方米?(图中单位:米)
30.(7分)某市供电局规定:居民用电高峰时收费为每千瓦时0.55元,低谷时收费为每千瓦时0.35元。某户在3月份共用电120千瓦时,缴纳电费58元。则该用户高峰时的用电量是多少千瓦时?(用方程解答)
安徽省合肥市2025-2026学年五年级上学期期末模拟数学预测卷
参考答案与试题解析
一.填空题(共10小题,满分18分)
1.(2分)8个2.4是 19.2 ,2.4中有8个 0.3 。
【考点】小数乘法;小数除法.
【专题】运算能力.
【答案】19.2,0.3。
【分析】求8个2.4是多少,用2.4乘8进行计算;求2.4中有8个几,用2.4除以8进行计算。
【解答】解:2.4×8=19.2
2.4÷8=0.3
答:8个2.4是19.2,2.4中有8个0.3。
故答案为:19.2,0.3。
【点评】本题主要考查了小数乘法、小数除法的计算,求几个几是多少,用乘法计算;求一个数里面有几个几,用除法计算。
2.(2分)若A×B=45,则(A×3)×B= 135 ,(A×2)×(B×5)= 450 。若A÷B=5……2,则(A×10)÷(B×10)= 5 …… 20 。
【考点】积的变化规律;商不变的规律(被除数和除数同时乘或除以相同不为零的数).
【专题】数据分析观念.
【答案】135;450;5,20。
【分析】一个因数不变,另一个因数乘几或除以几(0除外),积也乘或除以几;两个因数相乘,一个因数乘m或除以m(0除外),另一个因数乘n或除以n(0除外),积就乘mn或除以mn;被除数和除数都乘或除以一个相同的数(0除外),商不变,余数也同时乘或除以一个相同的数(0除外)。据此判断即可。
【解答】解:若A×B=45,则(A×3)×B=45×3=135;
(A×2)×(B×5)=45×(2×5)=450;
若A÷B=5……2,则(A×10)÷(B×10)=5……20。
故答案为:135;450;5,20。
【点评】熟练掌握积的变化规律和商的变化规律是解题的关键。
3.(2分)快快和乐乐在同一个班,乐乐的座位在第2列第5行,记作 (2,5) ;快快的位置在第5列第4行,记作 (5,4) 。
【考点】数对与位置.
【专题】数据分析观念;应用意识.
【答案】(2,5);(5,4)。
【分析】根据利用数对是物体位置的方法,用数对表示物体的位置时,列数在前,行数在后。据此解答。
【解答】解:快快和乐乐在同一个班,乐乐的座位在第2列第5行,记作(2,5);快快的位置在第5列第4行,记作(5,4)。
故答案为:(2,5);(5,4)。
【点评】此题考查的目的是理解掌握利用数对表示物体位置的方法及应用,关键是明确:用数对表示物体的位置时,列数在前,行数在后。
4.(1分)□+□=□×□(□表示同一个数)□= 2 .
【考点】含字母式子的求值.
【专题】运算顺序及法则.
【答案】见试题解答内容
【分析】由题意知,两个数相加的和等于这两个数的乘积,所以是2+2=2×2,□=2据此即可解答.
【解答】解:由分析知:
2+2=2×2,
所以□=2;
故答案为:2.
【点评】此题考查了两个数相加的和等于这两个数的乘积,这个数是2这个特例.
5.(3分)不计算,直接写出下面各题的积或商。
(1)
(2)
【考点】积的变化规律;商的变化规律.
【专题】计算题;运算能力.
【答案】(1)400;1600;800;(2)27;18;9。
【分析】积的变化规律:一个因数不变,另一个因数乘(或除以)几(0除外),积也乘(或除以)相同的数;
商的变化规律:在除法里,被除数和除数同时乘(或除以)相同的数(0除外),商不变。
在除法里,被除数不变,除数乘(或除以)几(0除外),商反而除以(或乘)相同的数。
在除法里,除数不变,被除数乘(或除以)几(0除外),商也随之乘(或除以)相同的数。据此解答即可。
【解答】解:(1)16×25,第一个因数不变,第二个因数除以2,积也除以2,所以:16×25=400;
32×50,第一个因数乘2,第二个因数不变,积也乘2,所以:32×50=1600;
32×25,第一个因数乘2,第二个因数除以2,积不变,所以:16×25=800;
(2)54÷2,被除数不变,除数除以3,商反而乘3,所以:54÷2=27;
108÷6,被除数乘2,除数不变,商也乘2,所以:108÷6=18;
216÷24,被除数和除数同时乘4,商不变,所以:216÷24=9。
【点评】熟练掌握积和商的变化规律是解答本题的关键。
6.(1分)每千克苹果a元,每千克香蕉b元,买5千克苹果要 5a 元,买7千克香蕉要 7b 元,买这两种水果一共花了 5a+7b 元.
【考点】用字母表示数.
【专题】用字母表示数.
【答案】见试题解答内容
【分析】根据单价×数量=总价即可解答,这里要注意字母与数字的乘积,可以省略乘号,数字放在前面,字母放在后面,由此即可解答.
【解答】解:根据题干分析可得:
买5千克苹果要5a元,
买7千克香蕉要7b元,
买这两种水果一共花了5a+7b元.
故答案为:5a;7b;5a+7b.
【点评】此题考查了单价、数量与总价的关系的灵活应用以及字母表示数的写法.
7.(2分)0.363636……的循环节是 36 ,用简便方法记作 0. ,保留三位小数是 0.364 。
【考点】循环小数及其分类;小数的近似数及其求法.
【专题】综合填空题;运算能力.
【答案】36;0.;0.364。
【分析】循环节是指循环小数的小数部分依次不断重复出现的一个或几个数字;从小数点后某一位开始不断地重复出现前一个或一节数字的十进制无限小数,叫做循环小数,循环小数的缩写法是将第一个循环节以后的数字全部略去,而在第一个循环节首末两位上方各添一个小点;根据四舍五入的取近似数的方法可知,保留三位小数,万分位上的数字是6,根据五入法进1即可。
【解答】解:0.363636……的循环节是36,用简便方法记作0.,保留三位小数是0.364。
故答案为:36;0.;0.364。
【点评】本题重点考查了循环小数的循环节、记法及按要求取近似值的方法。
8.(2分)一个三角形的底是6米,高是4米,它的面积是 12 平方米.
【考点】三角形的周长和面积.
【专题】平面图形的认识与计算.
【答案】见试题解答内容
【分析】三角形的面积=底×高÷2,代入数据即可求解.
【解答】解:6×4÷2=12(平方米);
答:这个三角形的面积是12平方米.
故答案为:12.
【点评】此题主要考查三角形的面积的计算方法的灵活应用.
9.(2分)如图所示的转盘停止转动后,指针最可能停在第 2 区域.指针停在奇数区域的可能性比停在偶数区域的可能性要 小 .
【考点】可能性的大小.
【专题】可能性;推理能力.
【答案】见试题解答内容
【分析】把转盘分成大小不等的5个区域,其中第2区域最大,指针最可能停在该区域;在1、2、3、4、5区域中,1、3、5为奇数,2、4为偶数,区域3与区域4相等,很容易看出,奇数区域虽然比偶数区域多1个,但偶数区域占的面积要大于奇数区域占的面积,因此,指针停在奇数区域的可能性比停在偶数区域的可能性要小.
【解答】解:如图
转盘停止转动后,指针最可能停在第2区域.指针停在奇数区域的可能性比停在偶数区域的可能性要小.
故答案为:2,小.
【点评】转盘上哪个区域面积大,指针停在该区域的可能性就大,反之,停在该区域的可能性就小.
10.(1分)观察前三个算式,找规律完成后面的算式。
143×63=9009
143×56=8008
143×49=7007
143×35= 5005
143× 21 =3003
【考点】“式”的规律.
【专题】计算题;运算能力.
【答案】5005;21。
【分析】仔细观察算式可知,前三个算式都有相同的乘数143,另一个乘数都是7的倍数(63是7的9倍,56是7的8倍,49是7的7倍)。乘得的积都是四位数且百位和十位上的数都是0,前面的一个乘数是7的几倍,积的个位和千位上的数就是几。在算式143×35中,35÷7=5,即35是7的5倍,所以143×35=5005。在算式143×=3003中,3003的个位和千位上都是3,7×3=21,所以143×21=3003。
【解答】解:根据分析可知:
143×35=5005
143×21=3003
故答案为:5005;21。
【点评】解答此题的关键是观察所给出的算式,找出算式之间数与数的关系,得出规律,再根据规律解决问题。
二.选择题(共10小题,满分20分,每小题2分)
11.(2分)某小学共有9个社团,人数最多的社团是42人,人数最少的社团是29人。对这所学校参加社团的总人数进行估计,结果正确的是( )
A.一定小于270人
B.一定大于400人
C.大于200人且小于400人
【考点】数的估算.
【专题】整数的认识;运算能力.
【答案】C
【分析】利用人数乘社团的数量,找出取值范围即可,注意利用估算的方法解答。
【解答】解:9×42≈360(人)
9×29≈270(人)
由此可知这所学校参加社团的总人数大于200人且小于400人。
故选:C。
【点评】本题考查了整数乘法的估算方法及应用。
12.(2分)如图线段图列出的方程正确的是( )
A.x+3x=380 B.3x+20=380
C.x+20×3=380
【考点】列方程解应用题(两步需要逆思考).
【专题】应用题;应用意识.
【答案】B
【分析】观察图可知:科普书有x本,文艺书的本数比科普书本数的3倍多20本,是380本,根据倍数关系可知:科普书的本数×3+20=文艺书的本数,由此列出方程求解。
【解答】解:由分析可知,下列线段图列出的方程正确的是:3x+20=380。
故选:B。
【点评】解答此题,首先弄清题意,分清已知与所求,再找出基本数量关系,由此列式或方程解答。
13.(2分)算式2.6÷0.8的商大致在如图中的位置( )处。
A.a B.b C.c D.d
【考点】小数除法.
【专题】运算能力.
【答案】D
【分析】根据小数除法的计算方法计算出2.6÷0.8的商,再在数轴上找到合适的位置即可。
【解答】解:2.6÷0.8=3.25
算式2.6÷0.8的商大致在如图中的位置d处。
故选:D。
【点评】本题主要考查了小数除法的计算以及学生对数轴的认识。
14.(2分)下列算式的结果在图中的大体位置表示正确的是( )
A.8.5×1.01 B.60.1÷5.9 C.6.1÷0.99
【考点】小数除法;小数乘法.
【专题】运算能力.
【答案】C
【分析】观察图形可知,C点表示的数在6到7之间,接近6;点A表示的数在8到9之间,接近8;点B表示的数在9到10之间,接近10;再根据小数乘除法的计算方法,分别求出各项的结果,再与图形中各点表示的数对比即可。
【解答】解:A.8.5×1.01=8.585,点A表示的数在8到9之间,接近8,小于8.5,不符合题意;
B.60.1÷5.9≈10.19,点B表示的数在9到10之间,接近10,不符合题意;
C.6.1÷0.99≈6.16,C点表示的数在6到7之间,接近6,符合题意。
故选:C。
【点评】本题主要考查了小数乘法、小数除法的运算以及学生对数轴的认识。
15.(2分)下列哪一句话是错误的( )
A.平行四边形两组对边分别平行
B.梯形有无数条高
C.平行线延长也可能相交
【考点】梯形的特征及分类;垂直与平行的特征及性质;平行四边形的特征及性质.
【专题】平面图形的认识与计算;数据分析观念.
【答案】C
【分析】A、根据平行四边形的意义,有两组对边分别平行的四边形叫做平行四边形判断;
B、根据梯形的高的含义,在梯形上底上任取一点,过这一点向下底作垂线段即为梯形的高.这样的线段可以作无数条,因而一个梯形能画出无数条高;
C、根据在同一平面内,延长之后永不相交的两条直线叫做平行线判断;据此解答即可。
【解答】解:由分析得出:
A、平行四边形两组对边分别平行说法正确;
B、梯形有无数条高说法正确;
C、平行线延长之后永不相交,所以平行线延长也可能相交说法错误;
故选:C。
【点评】此题主要考查平行和垂直的基本概念的掌握情况,要逐题分析。
16.(2分)观察图中的3个梯形.它们的面积相比较,( )
A.①最大 B.②最大 C.③最大 D.一样大
【考点】梯形的面积;组合图形的面积.
【专题】平面图形的认识与计算;几何直观.
【答案】D
【分析】观察图发现,这三个梯形的高相等,根据梯形的面积=(上底+下底)×高÷2可知,只要比较梯形的上下底的和,即可得出这三个梯形面积之间的关系.
【解答】解:三个梯形的高相等;
①上底与下底的和:3+5=8(个格子)
②上底与下底的和:2+6=8(个格子)
③上底与下底的和:1+7=8(个格子)
三个梯形上下底的和都是8个格子,相等,高也相当,所以这三个梯形的面积一样大.
故选:D.
【点评】熟练掌握梯形的面积公式是解决本题的关键.
17.(2分)5x=0,则方程( )
A.没有解 B.有无数个解
C.只有一个解
【考点】整数方程求解.
【专题】运算能力.
【答案】C
【分析】据等式的性质,在方程两边同时除以5,得出方程的解,据此选择。
【解答】解:5x=0
5x÷5=0÷5
x=0
所以方程5x=0的解只有一个,即x=0。
故选:C。
【点评】此题考查根据等式的性质解方程,即在等式两边同时加上、减去、乘上或除以一个数(0除外),等式的左右两边仍相等;注意等号上下要对齐。
18.(2分)有7名同学围坐一圈,张老师有75张卡片,她依次每人每次发一张,直到发完为止,得到多于10张卡片的学生有( )人。
A.5 B.6 C.10
【考点】有余数的除法应用题.
【专题】简单应用题和一般复合应用题;应用意识.
【答案】A
【分析】把75平均分成7份,求每份是多少,根据单一量=总量÷数量,求出每份是10张,余数是几,就有几个人得到多于10张卡片,即可解答。
【解答】解:75÷7=10(张)……5(张)
答:得到多于10张卡片的学生有5人。
故选:A。
【点评】本题考查的是有余数除法应用题,理解商和余数的意义是解答关键。
19.(2分)一个平行四边形的底不变,高扩大到原来的4倍,它的面积( )
A.不变 B.扩大到原来的2倍
C.扩大到原来的4倍 D.缩小到原来的
【考点】平行四边形的面积.
【专题】平面图形的认识与计算;几何直观;应用意识.
【答案】C
【分析】根据平行四边形的面积公式:S=ah,再根据因数与积的变化规律,一个因数不变,另一个因数扩大几倍,积也扩大相同的倍数.据此解答.
【解答】解:因为平行四边形的面积=底×高,所以一个平行四边形的底不变,高扩大到原来的4倍,它的面积扩大到原来的4倍.
故选:C.
【点评】此题主要考查平行四边形面积公式的灵活运用,因数与积的变化规律的应用.
20.(2分)在一条长300米的公路两边种树,每隔3米种一棵。两端都种,一共种( )棵。
A.100 B.101 C.201 D.202
【考点】植树问题.
【专题】推理能力.
【答案】D
【分析】已知在一条长300米的公路两边种树,每隔3米种一棵,根据“全长÷间距=间隔数”,先求出公路一边种树的间隔数;因为两端都种,那么棵数=间隔数+1,即可求出公路一边种树的棵数,再乘2,即是公路两边种树的棵数。
【解答】解:公路一边种了:
300÷3+1
=100+1
=101(棵)
公路两边一共种:
101×2=202(棵)
答:一共种202棵。
故选:D。
【点评】本题考查植树问题,掌握沿直线上栽树的三种情况:两端都栽时,棵数=间隔数+1;两端都不栽时,棵数=间隔数﹣1;一端栽一端不栽时,棵数=间隔数。
三.计算题(共4小题,满分33分)
21.(8分)列竖式计算下面各题,带*的要写出验算过程。
32.4×13= 20.5×2.6= *1.28×0.35=
27÷36= *9.01÷17= 0.76×1.4≈(结果保留两位小数)
【考点】小数乘法;小数除法.
【专题】运算顺序及法则;运算能力.
【答案】421.2;53.3;0.448;0.75;0.53;1.06。
【分析】小数乘法法则:先把被乘数和乘数都看作整数,按照整数的乘法法则进行计算,求出整数乘法的积,然后,再看被乘数和乘数一共有几位小数,就从积的右边起数出几位,点上小数点。如果小数的末尾出现0时,根据小数的基本性质,要把它去掉。用交换因数的位置再乘一遍进行验算。
当除数是整数时,可以直接按照整数除法的法则进行计算,商的小数点要与被除数的小数点对齐.如果有余数,就在余数的右边补上0,再继续除.商的整数部分或小数部分哪一位不够1时,要写上0,补足位数。
用被除数=商×除数进行验算。
【解答】解:32.4×13=421.2
20.5×2.6=53.3
*1.28×0.35=0.448
27÷36=0.75
*9.01÷17=0.53
0.76×1.4≈1.06
【点评】本题考查了小数乘法、小数除法的笔算及验算。
22.(7分)用竖式计算。
1.09×2.3
0.468÷0.65
【考点】小数乘法;小数除法.
【专题】计算题;运算能力.
【答案】2.507;0.72。
【分析】利用小数乘法,小数除法的计算方法,结合题中算式分别计算即可。
【解答】解:1.09×2.3=2.507
0.468÷0.65=0.72
【点评】本题考查的是小数乘法,小数除法的计算方法。
23.(12分)用简便方法计算。
(1)101×24﹣24 (2)6100÷25÷4 (3)23×46+23×54
【考点】运算定律与简便运算.
【专题】运算能力.
【答案】(1)2400;(2)61;(3)2300。
【分析】(1)根据乘法分配律简算;
(2)根据除法的性质简算;
(3)根据乘法分配律简算。
【解答】解:(1)101×24﹣24
=24×(101﹣1)
=24×100
=2400
(2)6100÷25÷4
=6100÷(25×4)
=6100÷100
=61
(3)23×46+23×54
=23×(46+54)
=23×100
=2300
【点评】完成本题要注意分析式中数据,运用合适的简便方法计算。
24.(6分)解方程。
3×(x+2.1)=10.5
(x﹣3)÷2=7.5
【考点】小数方程求解.
【专题】简易方程;运算能力.
【答案】x=1.4;x=18。
【分析】(1)根据等式的性质,方程两边先同时除以3,再同时减去2.1求解。
(2)根据等式的性质,方程两边先同时乘2,再同时加上3求解。
【解答】解:(1)3×(x+2.1)=10.5
3×(x+2.1)÷3=10.5÷3
x+2.1=3.5
x+2.1﹣2.1=3.5﹣2.1
x=1.4
(2)(x﹣3)÷2=7.5
(x﹣3)÷2×2=7.5×2
x﹣3=15
x﹣3+3=15+3
x=18
【点评】本题考查解方程,解题的关键是掌握等式的性质:方程两边同时加上或减去相同的数,等式仍然成立;方程两边同时乘(或除以)相同的数(0除外),等式仍然成立。
四.操作题(共1小题,满分5分,每小题5分)
25.(5分)三角形ABC的顶点在左边方格中的位置是A(3,6),B(1,2),C(3,0)。
(1)请在方格中画出三角形ABC,并画出三角形ABC向右平移3格后的图形。
(2)在方格中画一个和三角形ABC面积相等的平行四边形。
(3)在方格中画一个梯形,要求面积是三角形ABC的2倍。
【考点】数对与位置;梯形的特征及分类;平行四边形的面积;三角形的周长和面积;作平移后的图形.
【专题】综合题;应用意识.
【答案】(平行四边形和梯形画法不唯一)
【分析】(1)根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行,据此标出点A、点B和点C的位置,再顺次连接各点即可;然后根据作平移图形的方法:先确定要平移图形的关键点,确定平移的方向是朝哪移的,然后确定移动的长度(格子数),最后把各点连接成图;
(2)三角形的面积=底×高÷2,平行四边形的面积=底×高;依据三角形的面积,求出平行四边形的底与高的格数,从而画出平行四边形;
(3)梯形的面积=(上底+下底)×高÷2,依据三角形的面积,求出梯形的上底、下底与高的格数,从而画出梯形。
【解答】解:(1)三角形ABC的顶点A(3,6),B(1,2),C(3,0)三点在方格中的位置,以及三角形ABC向右平移3格后的图形,如下图所示:
(2)6×2÷2
=12÷2
=6
3×2=6
即画一个底为3,高为2的平行四边形即可,如下图所示:
(画法不唯一)
(3)6×2=12
(2+4)×4÷2
=6×4÷2
=24÷2
=12
即画一个上底为2,下底为4,高为4的梯形即可:
(画法不唯一)
【点评】本题考查三角形、平行四边形和梯形的面积,熟记公式是解题的关键,以及平行四边形和梯形的画法、图形的平移。
五.应用题(共5小题,满分24分)
26.(3分)学校共有620名同学参加大课间录像活动,如果要站成32列,平均每列多少名同学?还剩多少名同学?
【考点】有余数的除法应用题.
【专题】应用意识.
【答案】19名;12名。
【分析】用620除以列数,商就是平均每列的同学,余数就是剩余的同学,据此解答。
【解答】解:620÷32=19(名)……12(名)
答:平均每列19名同学,还剩12名同学。
【点评】本题重点考查有余数除法的应用,熟练掌握整数除法的计算方法是解答本题的关键。
27.(4分)加工一批零件,李师傅单独做,需要15天:赵师傅单独做,需要10天。两位师傅合作,多少天能完成任务?
【考点】简单的工程问题.
【专题】工程问题;应用意识.
【答案】6天。
【分析】将这批零件的总数看作单位“1”,李师傅的工作效率就是,赵师傅的工作效率是,再用工作总量“1“除以合作的工作效率和即可求出需要的时间。
【解答】解:1÷()
=1
=6(天)
答:6天能完成任务。
【点评】此题主要考查工作时间、工作效率、工作总量三者之间的数量关系,解答时往往把工作总量看作“1”,再利用它们的数量关系解答。
28.(5分)一块近似于平行四边形的草坪,中间有一条1米宽的石子路(如图)。如果铺1平方米的草坪需要18元,铺好这块草坪一共需要多少元?
【考点】平行四边形的面积.
【专题】平面图形的认识与计算;几何直观;应用意识.
【答案】铺好这块草坪一共需要3078元。
【分析】根据题意可知,草坪中间有一条宽为1米的小路,用整块草坪的底减去1米就是草坪的实际底,根据平行四边形的面积公式:S=ah,把数据代入公式求出草坪的面积,然后用草坪的面积乘每平方米的费用即可。
【解答】解:20﹣1=19(米)
19×9=171(平方米)
171×18=3078(元)
答:铺好这块草坪一共需要3078元。
【点评】此题主要考查平行四边形面积公式的灵活运用,关键是熟记公式。
29.(5分)如图,阴影部分表示铺设人造草坪的区域。人造草坪的面积是多少平方米?(图中单位:米)
【考点】组合图形的面积.
【专题】几何直观.
【答案】1550平方米。
【分析】根据图示,阴影部分的面积等于长方形的面积减去梯形的面积,根据长方形的面积=长×宽,梯形的面积=(上底+下底)×高÷2,解答即可。
【解答】解:60×30﹣(20+30)×10÷2
=1800﹣250
=1550(平方米)
答:人造草坪的面积是1550平方米。
【点评】本题考查了长方形和梯形面积公式的灵活运用,结合题意分析解答即可。
30.(7分)某市供电局规定:居民用电高峰时收费为每千瓦时0.55元,低谷时收费为每千瓦时0.35元。某户在3月份共用电120千瓦时,缴纳电费58元。则该用户高峰时的用电量是多少千瓦时?(用方程解答)
【考点】列方程解应用题(两步需要逆思考);整数、小数复合应用题.
【专题】应用意识.
【答案】80千瓦时。
【分析】设高峰期的用电量为x度,则低谷时用电量为(120﹣x)度,根据等量关系:高峰期的电费+低谷时的电费=58,可列出方程并求解。
【解答】解:设高峰期的用电量为x度,则低谷时用电量为(120﹣x)度。
0.55x+0.35×(120﹣x)=58
0.55x+0.35×120﹣0.35x=58
0.55x+42﹣0.35x=58
0.2x+42=58
0.2x+42﹣42=58﹣42
0.2x=16
0.2x÷0.2=16÷0.2
x=80
答:该用户高峰时的用电量是80千瓦时。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
安徽省合肥市2025-2026学年五年级上学期期末模拟数学预测卷
一.填空题(共10小题,满分18分)
1.(2分)8个2.4是 ,2.4中有8个 。
2.(2分)若A×B=45,则(A×3)×B= ,(A×2)×(B×5)= 。若A÷B=5……2,则(A×10)÷(B×10)= …… 。
3.(2分)快快和乐乐在同一个班,乐乐的座位在第2列第5行,记作 ;快快的位置在第5列第4行,记作 。
4.(1分)□+□=□×□(□表示同一个数)□= .
5.(3分)不计算,直接写出下面各题的积或商。
(1)
(2)
6.(1分)每千克苹果a元,每千克香蕉b元,买5千克苹果要 元,买7千克香蕉要 元,买这两种水果一共花了 元.
7.(2分)0.363636……的循环节是 ,用简便方法记作 ,保留三位小数是 。
8.(2分)一个三角形的底是6米,高是4米,它的面积是 平方米.
9.(2分)如图所示的转盘停止转动后,指针最可能停在第 区域.指针停在奇数区域的可能性比停在偶数区域的可能性要 .
10.(1分)观察前三个算式,找规律完成后面的算式。
143×63=9009
143×56=8008
143×49=7007
143×35=
143× =3003
二.选择题(共10小题,满分20分,每小题2分)
11.(2分)某小学共有9个社团,人数最多的社团是42人,人数最少的社团是29人。对这所学校参加社团的总人数进行估计,结果正确的是( )
A.一定小于270人
B.一定大于400人
C.大于200人且小于400人
12.(2分)如图线段图列出的方程正确的是( )
A.x+3x=380 B.3x+20=380
C.x+20×3=380
13.(2分)算式2.6÷0.8的商大致在如图中的位置( )处。
A.a B.b C.c D.d
14.(2分)下列算式的结果在图中的大体位置表示正确的是( )
A.8.5×1.01 B.60.1÷5.9 C.6.1÷0.99
15.(2分)下列哪一句话是错误的( )
A.平行四边形两组对边分别平行
B.梯形有无数条高
C.平行线延长也可能相交
16.(2分)观察图中的3个梯形.它们的面积相比较,( )
A.①最大 B.②最大 C.③最大 D.一样大
17.(2分)5x=0,则方程( )
A.没有解 B.有无数个解
C.只有一个解
18.(2分)有7名同学围坐一圈,张老师有75张卡片,她依次每人每次发一张,直到发完为止,得到多于10张卡片的学生有( )人。
A.5 B.6 C.10
19.(2分)一个平行四边形的底不变,高扩大到原来的4倍,它的面积( )
A.不变 B.扩大到原来的2倍
C.扩大到原来的4倍 D.缩小到原来的
20.(2分)在一条长300米的公路两边种树,每隔3米种一棵。两端都种,一共种( )棵。
A.100 B.101 C.201 D.202
三.计算题(共4小题,满分33分)
21.(8分)列竖式计算下面各题,带*的要写出验算过程。
32.4×13= 20.5×2.6= *1.28×0.35=
27÷36= *9.01÷17= 0.76×1.4≈(结果保留两位小数)
22.(7分)用竖式计算。
1.09×2.3
0.468÷0.65
23.(12分)用简便方法计算。
(1)101×24﹣24 (2)6100÷25÷4 (3)23×46+23×54
24.(6分)解方程。
3×(x+2.1)=10.5
(x﹣3)÷2=7.5
四.操作题(共1小题,满分5分,每小题5分)
25.(5分)三角形ABC的顶点在左边方格中的位置是A(3,6),B(1,2),C(3,0)。
(1)请在方格中画出三角形ABC,并画出三角形ABC向右平移3格后的图形。
(2)在方格中画一个和三角形ABC面积相等的平行四边形。
(3)在方格中画一个梯形,要求面积是三角形ABC的2倍。
五.应用题(共5小题,满分24分)
26.(3分)学校共有620名同学参加大课间录像活动,如果要站成32列,平均每列多少名同学?还剩多少名同学?
27.(4分)加工一批零件,李师傅单独做,需要15天:赵师傅单独做,需要10天。两位师傅合作,多少天能完成任务?
28.(5分)一块近似于平行四边形的草坪,中间有一条1米宽的石子路(如图)。如果铺1平方米的草坪需要18元,铺好这块草坪一共需要多少元?
29.(5分)如图,阴影部分表示铺设人造草坪的区域。人造草坪的面积是多少平方米?(图中单位:米)
30.(7分)某市供电局规定:居民用电高峰时收费为每千瓦时0.55元,低谷时收费为每千瓦时0.35元。某户在3月份共用电120千瓦时,缴纳电费58元。则该用户高峰时的用电量是多少千瓦时?(用方程解答)
安徽省合肥市2025-2026学年五年级上学期期末模拟数学预测卷
参考答案与试题解析
一.填空题(共10小题,满分18分)
1.(2分)8个2.4是 19.2 ,2.4中有8个 0.3 。
【考点】小数乘法;小数除法.
【专题】运算能力.
【答案】19.2,0.3。
【分析】求8个2.4是多少,用2.4乘8进行计算;求2.4中有8个几,用2.4除以8进行计算。
【解答】解:2.4×8=19.2
2.4÷8=0.3
答:8个2.4是19.2,2.4中有8个0.3。
故答案为:19.2,0.3。
【点评】本题主要考查了小数乘法、小数除法的计算,求几个几是多少,用乘法计算;求一个数里面有几个几,用除法计算。
2.(2分)若A×B=45,则(A×3)×B= 135 ,(A×2)×(B×5)= 450 。若A÷B=5……2,则(A×10)÷(B×10)= 5 …… 20 。
【考点】积的变化规律;商不变的规律(被除数和除数同时乘或除以相同不为零的数).
【专题】数据分析观念.
【答案】135;450;5,20。
【分析】一个因数不变,另一个因数乘几或除以几(0除外),积也乘或除以几;两个因数相乘,一个因数乘m或除以m(0除外),另一个因数乘n或除以n(0除外),积就乘mn或除以mn;被除数和除数都乘或除以一个相同的数(0除外),商不变,余数也同时乘或除以一个相同的数(0除外)。据此判断即可。
【解答】解:若A×B=45,则(A×3)×B=45×3=135;
(A×2)×(B×5)=45×(2×5)=450;
若A÷B=5……2,则(A×10)÷(B×10)=5……20。
故答案为:135;450;5,20。
【点评】熟练掌握积的变化规律和商的变化规律是解题的关键。
3.(2分)快快和乐乐在同一个班,乐乐的座位在第2列第5行,记作 (2,5) ;快快的位置在第5列第4行,记作 (5,4) 。
【考点】数对与位置.
【专题】数据分析观念;应用意识.
【答案】(2,5);(5,4)。
【分析】根据利用数对是物体位置的方法,用数对表示物体的位置时,列数在前,行数在后。据此解答。
【解答】解:快快和乐乐在同一个班,乐乐的座位在第2列第5行,记作(2,5);快快的位置在第5列第4行,记作(5,4)。
故答案为:(2,5);(5,4)。
【点评】此题考查的目的是理解掌握利用数对表示物体位置的方法及应用,关键是明确:用数对表示物体的位置时,列数在前,行数在后。
4.(1分)□+□=□×□(□表示同一个数)□= 2 .
【考点】含字母式子的求值.
【专题】运算顺序及法则.
【答案】见试题解答内容
【分析】由题意知,两个数相加的和等于这两个数的乘积,所以是2+2=2×2,□=2据此即可解答.
【解答】解:由分析知:
2+2=2×2,
所以□=2;
故答案为:2.
【点评】此题考查了两个数相加的和等于这两个数的乘积,这个数是2这个特例.
5.(3分)不计算,直接写出下面各题的积或商。
(1)
(2)
【考点】积的变化规律;商的变化规律.
【专题】计算题;运算能力.
【答案】(1)400;1600;800;(2)27;18;9。
【分析】积的变化规律:一个因数不变,另一个因数乘(或除以)几(0除外),积也乘(或除以)相同的数;
商的变化规律:在除法里,被除数和除数同时乘(或除以)相同的数(0除外),商不变。
在除法里,被除数不变,除数乘(或除以)几(0除外),商反而除以(或乘)相同的数。
在除法里,除数不变,被除数乘(或除以)几(0除外),商也随之乘(或除以)相同的数。据此解答即可。
【解答】解:(1)16×25,第一个因数不变,第二个因数除以2,积也除以2,所以:16×25=400;
32×50,第一个因数乘2,第二个因数不变,积也乘2,所以:32×50=1600;
32×25,第一个因数乘2,第二个因数除以2,积不变,所以:16×25=800;
(2)54÷2,被除数不变,除数除以3,商反而乘3,所以:54÷2=27;
108÷6,被除数乘2,除数不变,商也乘2,所以:108÷6=18;
216÷24,被除数和除数同时乘4,商不变,所以:216÷24=9。
【点评】熟练掌握积和商的变化规律是解答本题的关键。
6.(1分)每千克苹果a元,每千克香蕉b元,买5千克苹果要 5a 元,买7千克香蕉要 7b 元,买这两种水果一共花了 5a+7b 元.
【考点】用字母表示数.
【专题】用字母表示数.
【答案】见试题解答内容
【分析】根据单价×数量=总价即可解答,这里要注意字母与数字的乘积,可以省略乘号,数字放在前面,字母放在后面,由此即可解答.
【解答】解:根据题干分析可得:
买5千克苹果要5a元,
买7千克香蕉要7b元,
买这两种水果一共花了5a+7b元.
故答案为:5a;7b;5a+7b.
【点评】此题考查了单价、数量与总价的关系的灵活应用以及字母表示数的写法.
7.(2分)0.363636……的循环节是 36 ,用简便方法记作 0. ,保留三位小数是 0.364 。
【考点】循环小数及其分类;小数的近似数及其求法.
【专题】综合填空题;运算能力.
【答案】36;0.;0.364。
【分析】循环节是指循环小数的小数部分依次不断重复出现的一个或几个数字;从小数点后某一位开始不断地重复出现前一个或一节数字的十进制无限小数,叫做循环小数,循环小数的缩写法是将第一个循环节以后的数字全部略去,而在第一个循环节首末两位上方各添一个小点;根据四舍五入的取近似数的方法可知,保留三位小数,万分位上的数字是6,根据五入法进1即可。
【解答】解:0.363636……的循环节是36,用简便方法记作0.,保留三位小数是0.364。
故答案为:36;0.;0.364。
【点评】本题重点考查了循环小数的循环节、记法及按要求取近似值的方法。
8.(2分)一个三角形的底是6米,高是4米,它的面积是 12 平方米.
【考点】三角形的周长和面积.
【专题】平面图形的认识与计算.
【答案】见试题解答内容
【分析】三角形的面积=底×高÷2,代入数据即可求解.
【解答】解:6×4÷2=12(平方米);
答:这个三角形的面积是12平方米.
故答案为:12.
【点评】此题主要考查三角形的面积的计算方法的灵活应用.
9.(2分)如图所示的转盘停止转动后,指针最可能停在第 2 区域.指针停在奇数区域的可能性比停在偶数区域的可能性要 小 .
【考点】可能性的大小.
【专题】可能性;推理能力.
【答案】见试题解答内容
【分析】把转盘分成大小不等的5个区域,其中第2区域最大,指针最可能停在该区域;在1、2、3、4、5区域中,1、3、5为奇数,2、4为偶数,区域3与区域4相等,很容易看出,奇数区域虽然比偶数区域多1个,但偶数区域占的面积要大于奇数区域占的面积,因此,指针停在奇数区域的可能性比停在偶数区域的可能性要小.
【解答】解:如图
转盘停止转动后,指针最可能停在第2区域.指针停在奇数区域的可能性比停在偶数区域的可能性要小.
故答案为:2,小.
【点评】转盘上哪个区域面积大,指针停在该区域的可能性就大,反之,停在该区域的可能性就小.
10.(1分)观察前三个算式,找规律完成后面的算式。
143×63=9009
143×56=8008
143×49=7007
143×35= 5005
143× 21 =3003
【考点】“式”的规律.
【专题】计算题;运算能力.
【答案】5005;21。
【分析】仔细观察算式可知,前三个算式都有相同的乘数143,另一个乘数都是7的倍数(63是7的9倍,56是7的8倍,49是7的7倍)。乘得的积都是四位数且百位和十位上的数都是0,前面的一个乘数是7的几倍,积的个位和千位上的数就是几。在算式143×35中,35÷7=5,即35是7的5倍,所以143×35=5005。在算式143×=3003中,3003的个位和千位上都是3,7×3=21,所以143×21=3003。
【解答】解:根据分析可知:
143×35=5005
143×21=3003
故答案为:5005;21。
【点评】解答此题的关键是观察所给出的算式,找出算式之间数与数的关系,得出规律,再根据规律解决问题。
二.选择题(共10小题,满分20分,每小题2分)
11.(2分)某小学共有9个社团,人数最多的社团是42人,人数最少的社团是29人。对这所学校参加社团的总人数进行估计,结果正确的是( )
A.一定小于270人
B.一定大于400人
C.大于200人且小于400人
【考点】数的估算.
【专题】整数的认识;运算能力.
【答案】C
【分析】利用人数乘社团的数量,找出取值范围即可,注意利用估算的方法解答。
【解答】解:9×42≈360(人)
9×29≈270(人)
由此可知这所学校参加社团的总人数大于200人且小于400人。
故选:C。
【点评】本题考查了整数乘法的估算方法及应用。
12.(2分)如图线段图列出的方程正确的是( )
A.x+3x=380 B.3x+20=380
C.x+20×3=380
【考点】列方程解应用题(两步需要逆思考).
【专题】应用题;应用意识.
【答案】B
【分析】观察图可知:科普书有x本,文艺书的本数比科普书本数的3倍多20本,是380本,根据倍数关系可知:科普书的本数×3+20=文艺书的本数,由此列出方程求解。
【解答】解:由分析可知,下列线段图列出的方程正确的是:3x+20=380。
故选:B。
【点评】解答此题,首先弄清题意,分清已知与所求,再找出基本数量关系,由此列式或方程解答。
13.(2分)算式2.6÷0.8的商大致在如图中的位置( )处。
A.a B.b C.c D.d
【考点】小数除法.
【专题】运算能力.
【答案】D
【分析】根据小数除法的计算方法计算出2.6÷0.8的商,再在数轴上找到合适的位置即可。
【解答】解:2.6÷0.8=3.25
算式2.6÷0.8的商大致在如图中的位置d处。
故选:D。
【点评】本题主要考查了小数除法的计算以及学生对数轴的认识。
14.(2分)下列算式的结果在图中的大体位置表示正确的是( )
A.8.5×1.01 B.60.1÷5.9 C.6.1÷0.99
【考点】小数除法;小数乘法.
【专题】运算能力.
【答案】C
【分析】观察图形可知,C点表示的数在6到7之间,接近6;点A表示的数在8到9之间,接近8;点B表示的数在9到10之间,接近10;再根据小数乘除法的计算方法,分别求出各项的结果,再与图形中各点表示的数对比即可。
【解答】解:A.8.5×1.01=8.585,点A表示的数在8到9之间,接近8,小于8.5,不符合题意;
B.60.1÷5.9≈10.19,点B表示的数在9到10之间,接近10,不符合题意;
C.6.1÷0.99≈6.16,C点表示的数在6到7之间,接近6,符合题意。
故选:C。
【点评】本题主要考查了小数乘法、小数除法的运算以及学生对数轴的认识。
15.(2分)下列哪一句话是错误的( )
A.平行四边形两组对边分别平行
B.梯形有无数条高
C.平行线延长也可能相交
【考点】梯形的特征及分类;垂直与平行的特征及性质;平行四边形的特征及性质.
【专题】平面图形的认识与计算;数据分析观念.
【答案】C
【分析】A、根据平行四边形的意义,有两组对边分别平行的四边形叫做平行四边形判断;
B、根据梯形的高的含义,在梯形上底上任取一点,过这一点向下底作垂线段即为梯形的高.这样的线段可以作无数条,因而一个梯形能画出无数条高;
C、根据在同一平面内,延长之后永不相交的两条直线叫做平行线判断;据此解答即可。
【解答】解:由分析得出:
A、平行四边形两组对边分别平行说法正确;
B、梯形有无数条高说法正确;
C、平行线延长之后永不相交,所以平行线延长也可能相交说法错误;
故选:C。
【点评】此题主要考查平行和垂直的基本概念的掌握情况,要逐题分析。
16.(2分)观察图中的3个梯形.它们的面积相比较,( )
A.①最大 B.②最大 C.③最大 D.一样大
【考点】梯形的面积;组合图形的面积.
【专题】平面图形的认识与计算;几何直观.
【答案】D
【分析】观察图发现,这三个梯形的高相等,根据梯形的面积=(上底+下底)×高÷2可知,只要比较梯形的上下底的和,即可得出这三个梯形面积之间的关系.
【解答】解:三个梯形的高相等;
①上底与下底的和:3+5=8(个格子)
②上底与下底的和:2+6=8(个格子)
③上底与下底的和:1+7=8(个格子)
三个梯形上下底的和都是8个格子,相等,高也相当,所以这三个梯形的面积一样大.
故选:D.
【点评】熟练掌握梯形的面积公式是解决本题的关键.
17.(2分)5x=0,则方程( )
A.没有解 B.有无数个解
C.只有一个解
【考点】整数方程求解.
【专题】运算能力.
【答案】C
【分析】据等式的性质,在方程两边同时除以5,得出方程的解,据此选择。
【解答】解:5x=0
5x÷5=0÷5
x=0
所以方程5x=0的解只有一个,即x=0。
故选:C。
【点评】此题考查根据等式的性质解方程,即在等式两边同时加上、减去、乘上或除以一个数(0除外),等式的左右两边仍相等;注意等号上下要对齐。
18.(2分)有7名同学围坐一圈,张老师有75张卡片,她依次每人每次发一张,直到发完为止,得到多于10张卡片的学生有( )人。
A.5 B.6 C.10
【考点】有余数的除法应用题.
【专题】简单应用题和一般复合应用题;应用意识.
【答案】A
【分析】把75平均分成7份,求每份是多少,根据单一量=总量÷数量,求出每份是10张,余数是几,就有几个人得到多于10张卡片,即可解答。
【解答】解:75÷7=10(张)……5(张)
答:得到多于10张卡片的学生有5人。
故选:A。
【点评】本题考查的是有余数除法应用题,理解商和余数的意义是解答关键。
19.(2分)一个平行四边形的底不变,高扩大到原来的4倍,它的面积( )
A.不变 B.扩大到原来的2倍
C.扩大到原来的4倍 D.缩小到原来的
【考点】平行四边形的面积.
【专题】平面图形的认识与计算;几何直观;应用意识.
【答案】C
【分析】根据平行四边形的面积公式:S=ah,再根据因数与积的变化规律,一个因数不变,另一个因数扩大几倍,积也扩大相同的倍数.据此解答.
【解答】解:因为平行四边形的面积=底×高,所以一个平行四边形的底不变,高扩大到原来的4倍,它的面积扩大到原来的4倍.
故选:C.
【点评】此题主要考查平行四边形面积公式的灵活运用,因数与积的变化规律的应用.
20.(2分)在一条长300米的公路两边种树,每隔3米种一棵。两端都种,一共种( )棵。
A.100 B.101 C.201 D.202
【考点】植树问题.
【专题】推理能力.
【答案】D
【分析】已知在一条长300米的公路两边种树,每隔3米种一棵,根据“全长÷间距=间隔数”,先求出公路一边种树的间隔数;因为两端都种,那么棵数=间隔数+1,即可求出公路一边种树的棵数,再乘2,即是公路两边种树的棵数。
【解答】解:公路一边种了:
300÷3+1
=100+1
=101(棵)
公路两边一共种:
101×2=202(棵)
答:一共种202棵。
故选:D。
【点评】本题考查植树问题,掌握沿直线上栽树的三种情况:两端都栽时,棵数=间隔数+1;两端都不栽时,棵数=间隔数﹣1;一端栽一端不栽时,棵数=间隔数。
三.计算题(共4小题,满分33分)
21.(8分)列竖式计算下面各题,带*的要写出验算过程。
32.4×13= 20.5×2.6= *1.28×0.35=
27÷36= *9.01÷17= 0.76×1.4≈(结果保留两位小数)
【考点】小数乘法;小数除法.
【专题】运算顺序及法则;运算能力.
【答案】421.2;53.3;0.448;0.75;0.53;1.06。
【分析】小数乘法法则:先把被乘数和乘数都看作整数,按照整数的乘法法则进行计算,求出整数乘法的积,然后,再看被乘数和乘数一共有几位小数,就从积的右边起数出几位,点上小数点。如果小数的末尾出现0时,根据小数的基本性质,要把它去掉。用交换因数的位置再乘一遍进行验算。
当除数是整数时,可以直接按照整数除法的法则进行计算,商的小数点要与被除数的小数点对齐.如果有余数,就在余数的右边补上0,再继续除.商的整数部分或小数部分哪一位不够1时,要写上0,补足位数。
用被除数=商×除数进行验算。
【解答】解:32.4×13=421.2
20.5×2.6=53.3
*1.28×0.35=0.448
27÷36=0.75
*9.01÷17=0.53
0.76×1.4≈1.06
【点评】本题考查了小数乘法、小数除法的笔算及验算。
22.(7分)用竖式计算。
1.09×2.3
0.468÷0.65
【考点】小数乘法;小数除法.
【专题】计算题;运算能力.
【答案】2.507;0.72。
【分析】利用小数乘法,小数除法的计算方法,结合题中算式分别计算即可。
【解答】解:1.09×2.3=2.507
0.468÷0.65=0.72
【点评】本题考查的是小数乘法,小数除法的计算方法。
23.(12分)用简便方法计算。
(1)101×24﹣24 (2)6100÷25÷4 (3)23×46+23×54
【考点】运算定律与简便运算.
【专题】运算能力.
【答案】(1)2400;(2)61;(3)2300。
【分析】(1)根据乘法分配律简算;
(2)根据除法的性质简算;
(3)根据乘法分配律简算。
【解答】解:(1)101×24﹣24
=24×(101﹣1)
=24×100
=2400
(2)6100÷25÷4
=6100÷(25×4)
=6100÷100
=61
(3)23×46+23×54
=23×(46+54)
=23×100
=2300
【点评】完成本题要注意分析式中数据,运用合适的简便方法计算。
24.(6分)解方程。
3×(x+2.1)=10.5
(x﹣3)÷2=7.5
【考点】小数方程求解.
【专题】简易方程;运算能力.
【答案】x=1.4;x=18。
【分析】(1)根据等式的性质,方程两边先同时除以3,再同时减去2.1求解。
(2)根据等式的性质,方程两边先同时乘2,再同时加上3求解。
【解答】解:(1)3×(x+2.1)=10.5
3×(x+2.1)÷3=10.5÷3
x+2.1=3.5
x+2.1﹣2.1=3.5﹣2.1
x=1.4
(2)(x﹣3)÷2=7.5
(x﹣3)÷2×2=7.5×2
x﹣3=15
x﹣3+3=15+3
x=18
【点评】本题考查解方程,解题的关键是掌握等式的性质:方程两边同时加上或减去相同的数,等式仍然成立;方程两边同时乘(或除以)相同的数(0除外),等式仍然成立。
四.操作题(共1小题,满分5分,每小题5分)
25.(5分)三角形ABC的顶点在左边方格中的位置是A(3,6),B(1,2),C(3,0)。
(1)请在方格中画出三角形ABC,并画出三角形ABC向右平移3格后的图形。
(2)在方格中画一个和三角形ABC面积相等的平行四边形。
(3)在方格中画一个梯形,要求面积是三角形ABC的2倍。
【考点】数对与位置;梯形的特征及分类;平行四边形的面积;三角形的周长和面积;作平移后的图形.
【专题】综合题;应用意识.
【答案】(平行四边形和梯形画法不唯一)
【分析】(1)根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行,据此标出点A、点B和点C的位置,再顺次连接各点即可;然后根据作平移图形的方法:先确定要平移图形的关键点,确定平移的方向是朝哪移的,然后确定移动的长度(格子数),最后把各点连接成图;
(2)三角形的面积=底×高÷2,平行四边形的面积=底×高;依据三角形的面积,求出平行四边形的底与高的格数,从而画出平行四边形;
(3)梯形的面积=(上底+下底)×高÷2,依据三角形的面积,求出梯形的上底、下底与高的格数,从而画出梯形。
【解答】解:(1)三角形ABC的顶点A(3,6),B(1,2),C(3,0)三点在方格中的位置,以及三角形ABC向右平移3格后的图形,如下图所示:
(2)6×2÷2
=12÷2
=6
3×2=6
即画一个底为3,高为2的平行四边形即可,如下图所示:
(画法不唯一)
(3)6×2=12
(2+4)×4÷2
=6×4÷2
=24÷2
=12
即画一个上底为2,下底为4,高为4的梯形即可:
(画法不唯一)
【点评】本题考查三角形、平行四边形和梯形的面积,熟记公式是解题的关键,以及平行四边形和梯形的画法、图形的平移。
五.应用题(共5小题,满分24分)
26.(3分)学校共有620名同学参加大课间录像活动,如果要站成32列,平均每列多少名同学?还剩多少名同学?
【考点】有余数的除法应用题.
【专题】应用意识.
【答案】19名;12名。
【分析】用620除以列数,商就是平均每列的同学,余数就是剩余的同学,据此解答。
【解答】解:620÷32=19(名)……12(名)
答:平均每列19名同学,还剩12名同学。
【点评】本题重点考查有余数除法的应用,熟练掌握整数除法的计算方法是解答本题的关键。
27.(4分)加工一批零件,李师傅单独做,需要15天:赵师傅单独做,需要10天。两位师傅合作,多少天能完成任务?
【考点】简单的工程问题.
【专题】工程问题;应用意识.
【答案】6天。
【分析】将这批零件的总数看作单位“1”,李师傅的工作效率就是,赵师傅的工作效率是,再用工作总量“1“除以合作的工作效率和即可求出需要的时间。
【解答】解:1÷()
=1
=6(天)
答:6天能完成任务。
【点评】此题主要考查工作时间、工作效率、工作总量三者之间的数量关系,解答时往往把工作总量看作“1”,再利用它们的数量关系解答。
28.(5分)一块近似于平行四边形的草坪,中间有一条1米宽的石子路(如图)。如果铺1平方米的草坪需要18元,铺好这块草坪一共需要多少元?
【考点】平行四边形的面积.
【专题】平面图形的认识与计算;几何直观;应用意识.
【答案】铺好这块草坪一共需要3078元。
【分析】根据题意可知,草坪中间有一条宽为1米的小路,用整块草坪的底减去1米就是草坪的实际底,根据平行四边形的面积公式:S=ah,把数据代入公式求出草坪的面积,然后用草坪的面积乘每平方米的费用即可。
【解答】解:20﹣1=19(米)
19×9=171(平方米)
171×18=3078(元)
答:铺好这块草坪一共需要3078元。
【点评】此题主要考查平行四边形面积公式的灵活运用,关键是熟记公式。
29.(5分)如图,阴影部分表示铺设人造草坪的区域。人造草坪的面积是多少平方米?(图中单位:米)
【考点】组合图形的面积.
【专题】几何直观.
【答案】1550平方米。
【分析】根据图示,阴影部分的面积等于长方形的面积减去梯形的面积,根据长方形的面积=长×宽,梯形的面积=(上底+下底)×高÷2,解答即可。
【解答】解:60×30﹣(20+30)×10÷2
=1800﹣250
=1550(平方米)
答:人造草坪的面积是1550平方米。
【点评】本题考查了长方形和梯形面积公式的灵活运用,结合题意分析解答即可。
30.(7分)某市供电局规定:居民用电高峰时收费为每千瓦时0.55元,低谷时收费为每千瓦时0.35元。某户在3月份共用电120千瓦时,缴纳电费58元。则该用户高峰时的用电量是多少千瓦时?(用方程解答)
【考点】列方程解应用题(两步需要逆思考);整数、小数复合应用题.
【专题】应用意识.
【答案】80千瓦时。
【分析】设高峰期的用电量为x度,则低谷时用电量为(120﹣x)度,根据等量关系:高峰期的电费+低谷时的电费=58,可列出方程并求解。
【解答】解:设高峰期的用电量为x度,则低谷时用电量为(120﹣x)度。
0.55x+0.35×(120﹣x)=58
0.55x+0.35×120﹣0.35x=58
0.55x+42﹣0.35x=58
0.2x+42=58
0.2x+42﹣42=58﹣42
0.2x=16
0.2x÷0.2=16÷0.2
x=80
答:该用户高峰时的用电量是80千瓦时。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
