第七章 相交线与平行线 综合测试题
图片预览
文档简介
第七章
相交线与平行线
综合测试题
(45分钟
100分)
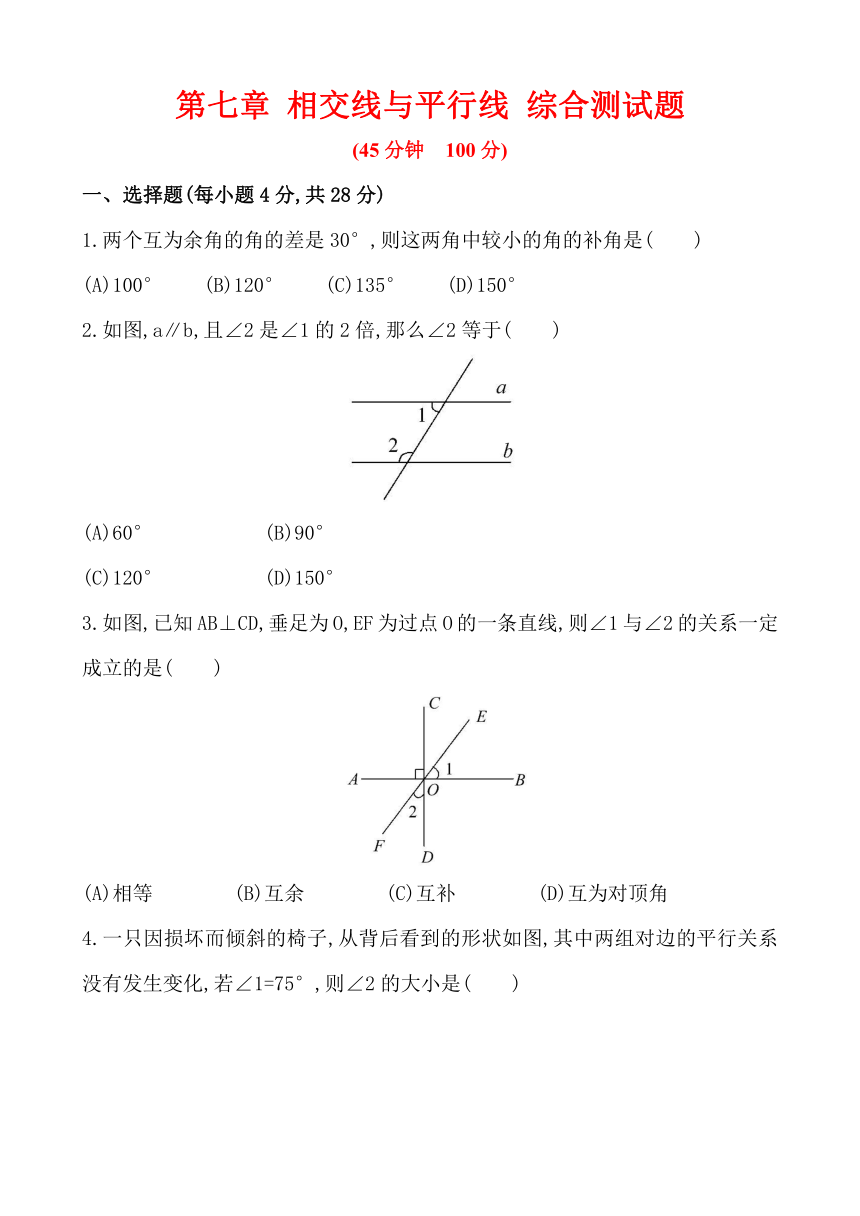
一、选择题(每小题4分,共28分)
1.两个互为余角的角的差是30°,则这两角中较小的角的补角是( )
(A)100°
(B)120°
(C)135°
(D)150°
2.如图,a∥b,且∠2是∠1的2倍,那么∠2等于( )
(A)60°
(B)90°
(C)120°
(D)150°
3.如图,已知AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )
(A)相等
(B)互余
(C)互补
(D)互为对顶角
4.一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的平行关系没有发生变化,若∠1=75°,则∠2的大小是( )
(A)75°
(B)115°
(C)65°
(D)105°
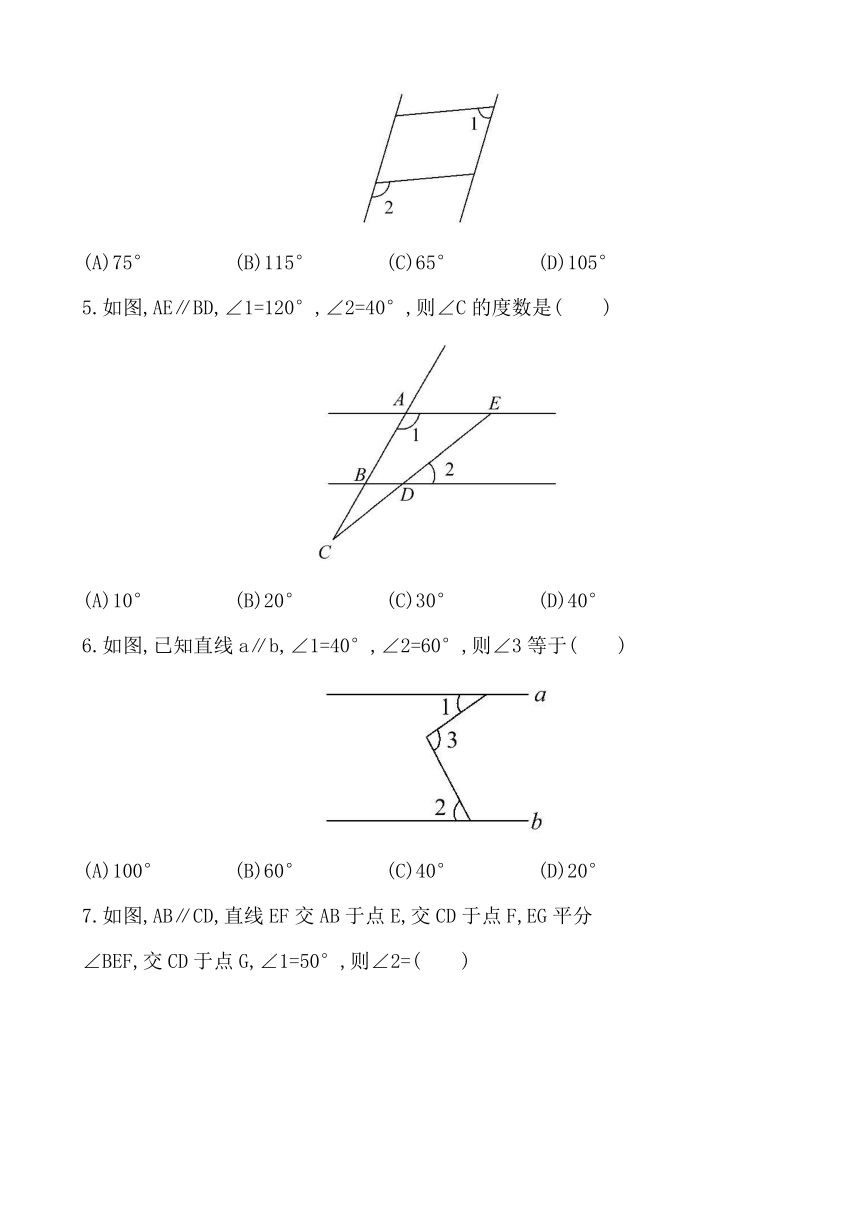
5.如图,AE∥BD,∠1=120°,∠2=40°,则∠C的度数是( )
(A)10°
(B)20°
(C)30°
(D)40°
6.如图,已知直线a∥b,∠1=40°,∠2=60°,则∠3等于( )
(A)100°
(B)60°
(C)40°
(D)20°
7.如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分
∠BEF,交CD于点G,∠1=50°,则∠2=( )
(A)50°
(B)60°
(C)65°
(D)90°
二、填空题(每小题5分,共25分)
8.已知∠AOB=40°,OC平分∠AOB,则∠AOC的补角等于 .
9.已知∠A=40°,则∠A的余角的度数是 .
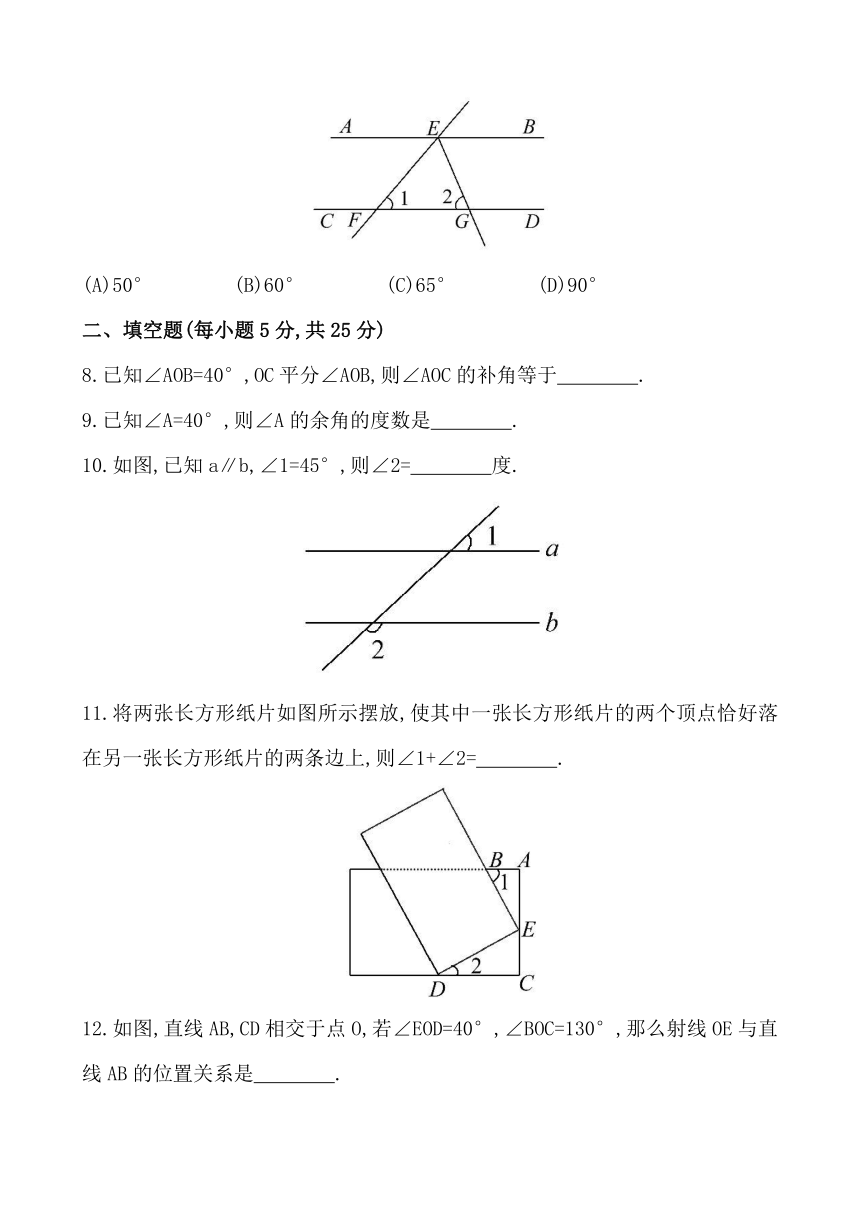
10.如图,已知a∥b,∠1=45°,则∠2= 度.
11.将两张长方形纸片如图所示摆放,使其中一张长方形纸片的两个顶点恰好落在另一张长方形纸片的两条边上,则∠1+∠2= .
12.如图,直线AB,CD相交于点O,若∠EOD=40°,∠BOC=130°,那么射线OE与直线AB的位置关系是 .
三、解答题(共47分)
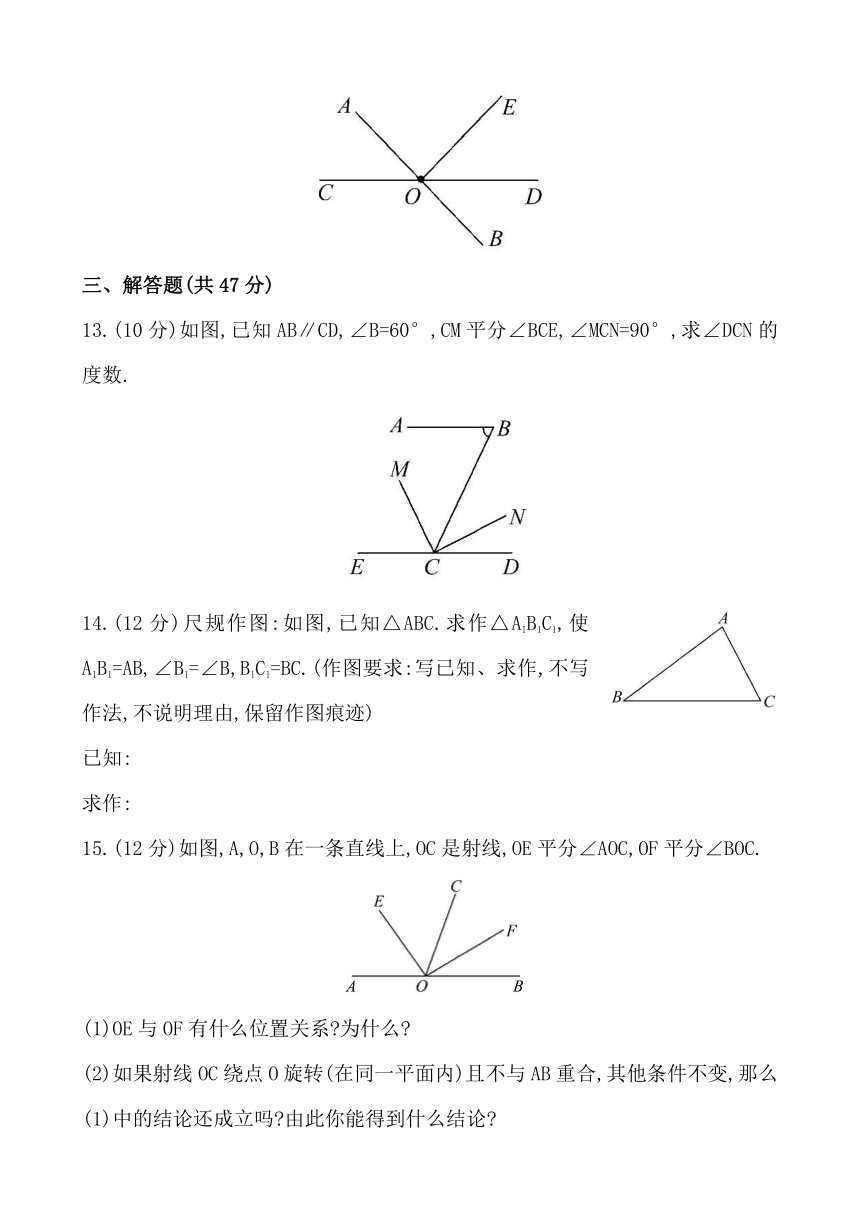
13.(10分)如图,已知AB∥CD,∠B=60°,CM平分∠BCE,∠MCN=90°,求∠DCN的度数.
14.(12分)尺规作图:如图,已知△ABC.求作△A1B1C1,使A1B1=AB,∠B1=∠B,B1C1=BC.(作图要求:写已知、求作,不写作法,不说明理由,保留作图痕迹)
已知:
求作:
15.(12分)如图,A,O,B在一条直线上,OC是射线,OE平分∠AOC,OF平分∠BOC.
(1)OE与OF有什么位置关系 为什么
(2)如果射线OC绕点O旋转(在同一平面内)且不与AB重合,其他条件不变,那么(1)中的结论还成立吗 由此你能得到什么结论
16.(13分)已知:如图,AB∥CD,试解决下列问题:
(1)∠1+∠2= .
(2)∠1+∠2+∠3= .
(3)∠1+∠2+∠3+∠4= .
(4)试探究∠1+∠2+∠3+∠4+…+∠n= .
答案解析
1.【解析】选D.设较小角为x°,则它的余角为(90-x)°,由题意可得90-x-x=30.解得:x=30,所以较小角的补角为180°-30°=150°.
2.【解析】选C.因为a∥b,所以∠2+∠1=180°.又因为∠2是∠1的2倍,所以
3∠1=180°,所以∠1=60°,所以∠2=120°.
3.【解析】选B.因为AB⊥CD,所以∠BOD=90°,所以∠1+∠2=90°,所以∠1与
∠2互余.
4.【解析】选D.因为两组对边分别平行,
所以∠1=∠3=75°,∠2+∠3=180°,
所以∠2=105°.
5.【解析】选B.因为直线AE∥BD,所以∠AEC=∠2=40°.
又因为∠1+∠AEC+∠C=180°,所以∠C=20°.
6.【解析】选A.过∠3的顶点作直线a的平行线,由平行线的性质可得∠3=∠1+∠2=40°+60°=100°.
7.【解析】选C.AB∥CD,∠1=50°,所以∠BEF=130°,EG平分∠BEF,所以∠BEG=
65°,又AB∥CD,所以∠2=∠BEG=65°.
8.【解析】因为OC平分∠AOB,∠AOB=40°,
所以∠AOC=20°,所以其补角为180°-20°=160°.
答案:160°
9.【解析】因为∠A=40°,所以∠A的余角的度数是90°-40°=50°.
答案:50°
10.【解析】因为a∥b,所以∠3=∠1=45°,因为∠3+∠2=180°,所以∠2=135°.
答案:135
11.【解析】如图,过点E作EF∥AB,则EF∥CD,
所以∠3=∠1,∠4=∠2,
所以∠1+∠2=∠3+∠4=90°.
答案:90°
12.【解析】由对顶角相等得∠AOD=∠BOC=130°,又因为∠EOD=40°,所以
∠AOE=130°-40°=90°,所以射线OE与直线AB垂直.
答案:垂直
13.【解析】因为AB∥CD(已知),
所以∠B+∠BCE=180°(两直线平行,同旁内角互补),
∠BCD=∠B=60°(两直线平行,内错角相等),
所以∠BCE=180°-∠B=180°-60°=120°.
又因为CM平分∠BCE(已知),
所以∠BCM=∠BCE=60°(角平分线的性质).
又因为∠MCN=∠BCM+∠BCN=90°,
所以∠BCN=30°,
因为∠BCD=∠BCN+∠DCN=60°,
所以∠DCN=30°.
14.【解析】已知:△ABC.
求作:△A1B1C1,使A1B1=AB,∠B1=∠B,B1C1=BC.
15.【解析】(1)OE⊥OF.
因为∠EOC=
QUOTE
∠AOC,∠COF=
QUOTE
∠BOC,
所以∠EOC+∠COF=
QUOTE
(∠AOC+∠BOC).
因为∠AOC+∠BOC=180°(平角定义),
所以∠EOC+∠COF=
QUOTE
×180°=90°.
所以OE⊥OF.
(2)成立.
邻补角的角平分线互相垂直.
16.【解析】(1)因为AB∥CD,所以∠1+∠2=180°.
(2)过点E作直线EM∥AB,因为AB∥CD,
所以EM∥CD,所以可得∠1+∠2+∠3=360°.
(3)过点E,F分别作直线EM∥AB,FN∥AB,与(2)同理可得EM∥CD∥FN∥AB,所以可得∠1+∠2+∠3+∠4=540°.
(4)同理可得∠1+∠2+∠3+∠4+…+∠n
=(n-1)180°.
相交线与平行线
综合测试题
(45分钟
100分)
一、选择题(每小题4分,共28分)
1.两个互为余角的角的差是30°,则这两角中较小的角的补角是( )
(A)100°
(B)120°
(C)135°
(D)150°
2.如图,a∥b,且∠2是∠1的2倍,那么∠2等于( )
(A)60°
(B)90°
(C)120°
(D)150°
3.如图,已知AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )
(A)相等
(B)互余
(C)互补
(D)互为对顶角
4.一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的平行关系没有发生变化,若∠1=75°,则∠2的大小是( )
(A)75°
(B)115°
(C)65°
(D)105°
5.如图,AE∥BD,∠1=120°,∠2=40°,则∠C的度数是( )
(A)10°
(B)20°
(C)30°
(D)40°
6.如图,已知直线a∥b,∠1=40°,∠2=60°,则∠3等于( )
(A)100°
(B)60°
(C)40°
(D)20°
7.如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分
∠BEF,交CD于点G,∠1=50°,则∠2=( )
(A)50°
(B)60°
(C)65°
(D)90°
二、填空题(每小题5分,共25分)
8.已知∠AOB=40°,OC平分∠AOB,则∠AOC的补角等于 .
9.已知∠A=40°,则∠A的余角的度数是 .
10.如图,已知a∥b,∠1=45°,则∠2= 度.
11.将两张长方形纸片如图所示摆放,使其中一张长方形纸片的两个顶点恰好落在另一张长方形纸片的两条边上,则∠1+∠2= .
12.如图,直线AB,CD相交于点O,若∠EOD=40°,∠BOC=130°,那么射线OE与直线AB的位置关系是 .
三、解答题(共47分)
13.(10分)如图,已知AB∥CD,∠B=60°,CM平分∠BCE,∠MCN=90°,求∠DCN的度数.
14.(12分)尺规作图:如图,已知△ABC.求作△A1B1C1,使A1B1=AB,∠B1=∠B,B1C1=BC.(作图要求:写已知、求作,不写作法,不说明理由,保留作图痕迹)
已知:
求作:
15.(12分)如图,A,O,B在一条直线上,OC是射线,OE平分∠AOC,OF平分∠BOC.
(1)OE与OF有什么位置关系 为什么
(2)如果射线OC绕点O旋转(在同一平面内)且不与AB重合,其他条件不变,那么(1)中的结论还成立吗 由此你能得到什么结论
16.(13分)已知:如图,AB∥CD,试解决下列问题:
(1)∠1+∠2= .
(2)∠1+∠2+∠3= .
(3)∠1+∠2+∠3+∠4= .
(4)试探究∠1+∠2+∠3+∠4+…+∠n= .
答案解析
1.【解析】选D.设较小角为x°,则它的余角为(90-x)°,由题意可得90-x-x=30.解得:x=30,所以较小角的补角为180°-30°=150°.
2.【解析】选C.因为a∥b,所以∠2+∠1=180°.又因为∠2是∠1的2倍,所以
3∠1=180°,所以∠1=60°,所以∠2=120°.
3.【解析】选B.因为AB⊥CD,所以∠BOD=90°,所以∠1+∠2=90°,所以∠1与
∠2互余.
4.【解析】选D.因为两组对边分别平行,
所以∠1=∠3=75°,∠2+∠3=180°,
所以∠2=105°.
5.【解析】选B.因为直线AE∥BD,所以∠AEC=∠2=40°.
又因为∠1+∠AEC+∠C=180°,所以∠C=20°.
6.【解析】选A.过∠3的顶点作直线a的平行线,由平行线的性质可得∠3=∠1+∠2=40°+60°=100°.
7.【解析】选C.AB∥CD,∠1=50°,所以∠BEF=130°,EG平分∠BEF,所以∠BEG=
65°,又AB∥CD,所以∠2=∠BEG=65°.
8.【解析】因为OC平分∠AOB,∠AOB=40°,
所以∠AOC=20°,所以其补角为180°-20°=160°.
答案:160°
9.【解析】因为∠A=40°,所以∠A的余角的度数是90°-40°=50°.
答案:50°
10.【解析】因为a∥b,所以∠3=∠1=45°,因为∠3+∠2=180°,所以∠2=135°.
答案:135
11.【解析】如图,过点E作EF∥AB,则EF∥CD,
所以∠3=∠1,∠4=∠2,
所以∠1+∠2=∠3+∠4=90°.
答案:90°
12.【解析】由对顶角相等得∠AOD=∠BOC=130°,又因为∠EOD=40°,所以
∠AOE=130°-40°=90°,所以射线OE与直线AB垂直.
答案:垂直
13.【解析】因为AB∥CD(已知),
所以∠B+∠BCE=180°(两直线平行,同旁内角互补),
∠BCD=∠B=60°(两直线平行,内错角相等),
所以∠BCE=180°-∠B=180°-60°=120°.
又因为CM平分∠BCE(已知),
所以∠BCM=∠BCE=60°(角平分线的性质).
又因为∠MCN=∠BCM+∠BCN=90°,
所以∠BCN=30°,
因为∠BCD=∠BCN+∠DCN=60°,
所以∠DCN=30°.
14.【解析】已知:△ABC.
求作:△A1B1C1,使A1B1=AB,∠B1=∠B,B1C1=BC.
15.【解析】(1)OE⊥OF.
因为∠EOC=
QUOTE
∠AOC,∠COF=
QUOTE
∠BOC,
所以∠EOC+∠COF=
QUOTE
(∠AOC+∠BOC).
因为∠AOC+∠BOC=180°(平角定义),
所以∠EOC+∠COF=
QUOTE
×180°=90°.
所以OE⊥OF.
(2)成立.
邻补角的角平分线互相垂直.
16.【解析】(1)因为AB∥CD,所以∠1+∠2=180°.
(2)过点E作直线EM∥AB,因为AB∥CD,
所以EM∥CD,所以可得∠1+∠2+∠3=360°.
(3)过点E,F分别作直线EM∥AB,FN∥AB,与(2)同理可得EM∥CD∥FN∥AB,所以可得∠1+∠2+∠3+∠4=540°.
(4)同理可得∠1+∠2+∠3+∠4+…+∠n
=(n-1)180°.
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
