1.1《三角形中的线段和角》小节复习题(含详解)--苏科版八年级数学上册
文档属性
| 名称 | 1.1《三角形中的线段和角》小节复习题(含详解)--苏科版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-06 05:56:46 | ||
图片预览



文档简介
1.1《三角形中的线段和角》小节复习题
题型01 确定三角形的条件
1.以下列各组数为边,能组成三角形的是( )
A. B. C. D.
2.下列长度的线段能组成三角形的是( )
A.2,4,8 B.5,5,10 C.2,10,13 D.3,6,8
3.下列每组数分别是三根小木棒的长度,将它们首尾顺次相接,能摆成三角形的是( )
A.3,4,7 B.6,8,15 C.5,12,13 D.5,5,11
4.将周长为的三角形的三条边依次放在一条直线上,其中所标数据正确的是( )
A. B.
C. D.
题型02 求三角形第三边的取值范围
1.等腰三角形的周长为16厘米,腰长为厘米,底边长为厘米,其中的取值范围是 .
2.已知 ABC的三边长为a、b、c,其中,则边长c的取值范围是 .
3.已知某三角形的三边长分别为,,,其中为正整数,则满足条件的值的和为 .
题型03 根据三角形的三边关系求值
1.已知三角形的两边长分别是和,选一个你喜欢的奇数作第三边,则该三角形的周长是 .
2.一个三角形的两边长分别是2和5,另一边长为偶数,则这个三角形的周长为 .
3.已知 ABC的两边长分别为2和,则能使得第三边长取到10的最小正整数是( )
A.5 B.6 C.7 D.8
4.三角形的两边长分别是、,周长是偶数并且是7的倍数,则第三边的长度是( )
A. B. C. D.
题型04 三角形的三边关系的实际运用
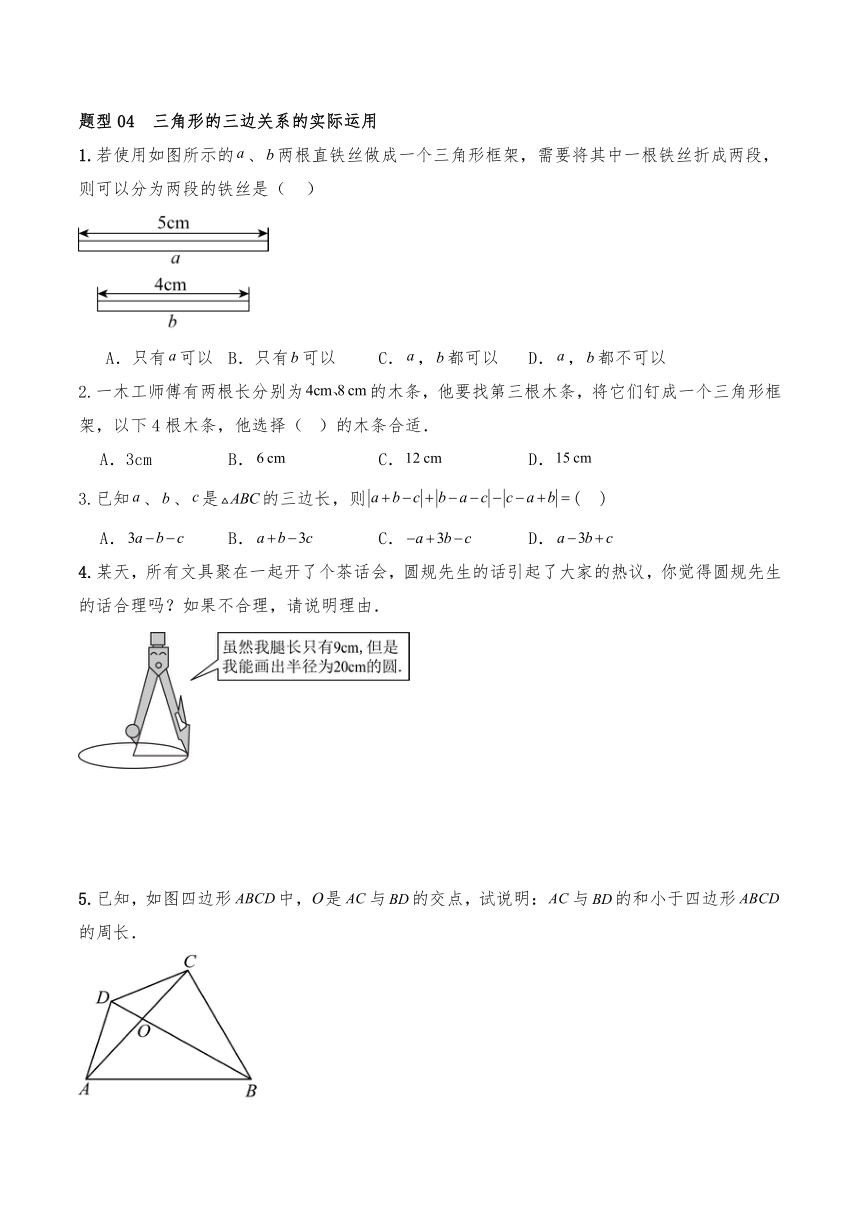
1.若使用如图所示的、两根直铁丝做成一个三角形框架,需要将其中一根铁丝折成两段,则可以分为两段的铁丝是( )
A.只有可以 B.只有可以 C.,都可以 D.,都不可以
2.一木工师傅有两根长分别为的木条,他要找第三根木条,将它们钉成一个三角形框架,以下4根木条,他选择( )的木条合适.
A.3cm B. C. D.
3.已知、、是的三边长,则( )
A. B. C. D.
4.某天,所有文具聚在一起开了个茶话会,圆规先生的话引起了大家的热议,你觉得圆规先生的话合理吗?如果不合理,请说明理由.
5.已知,如图四边形中,是与的交点,试说明:与的和小于四边形的周长.
题型05 中线平分三角形的面积
1.如图,已知 ABC的面积为,分别延长至点,使,延长至点,使,延长至点,使,依次连接,,,则阴影部分的面积为( )
A. B. C. D.
2.如图,是 ABC的中线,是的中线,若 ABC的面积为12,则的面积为( )
A.3 B.4 C.6 D.8
3.如图所示,在 ABC中,D、E、F分别为的中点,且,则的面积等于( )
A. B. C. D.
4.如图,在 ABC中,点D是的中点,连接,点E在上,且,于点F.若,,则 ABC的面积为( )
A.50 B.55 C.60 D.65
5.如图,对面积为的 ABC逐次进行以下操作:第一次操作,分别延长、、至点、、,使得,,,顺次连接、、,得到,记其面积为;第二次操作,分别延长、、至点、、,使得,,,顺次连接、、,得到,记其面积为;…; 按此规律继续下去,可得到 A5B5C5,则其面积为 ( )
A. B. C. D.
题型06 中线中的周长差与边的差
1.如图, ABC中,,,是 ABC的中线,则的周长比的周长大 .
2.如图, ABC的周长是,是边上的中线,,,则与的周长之差为( )
A.2 B.3 C.4 D.6
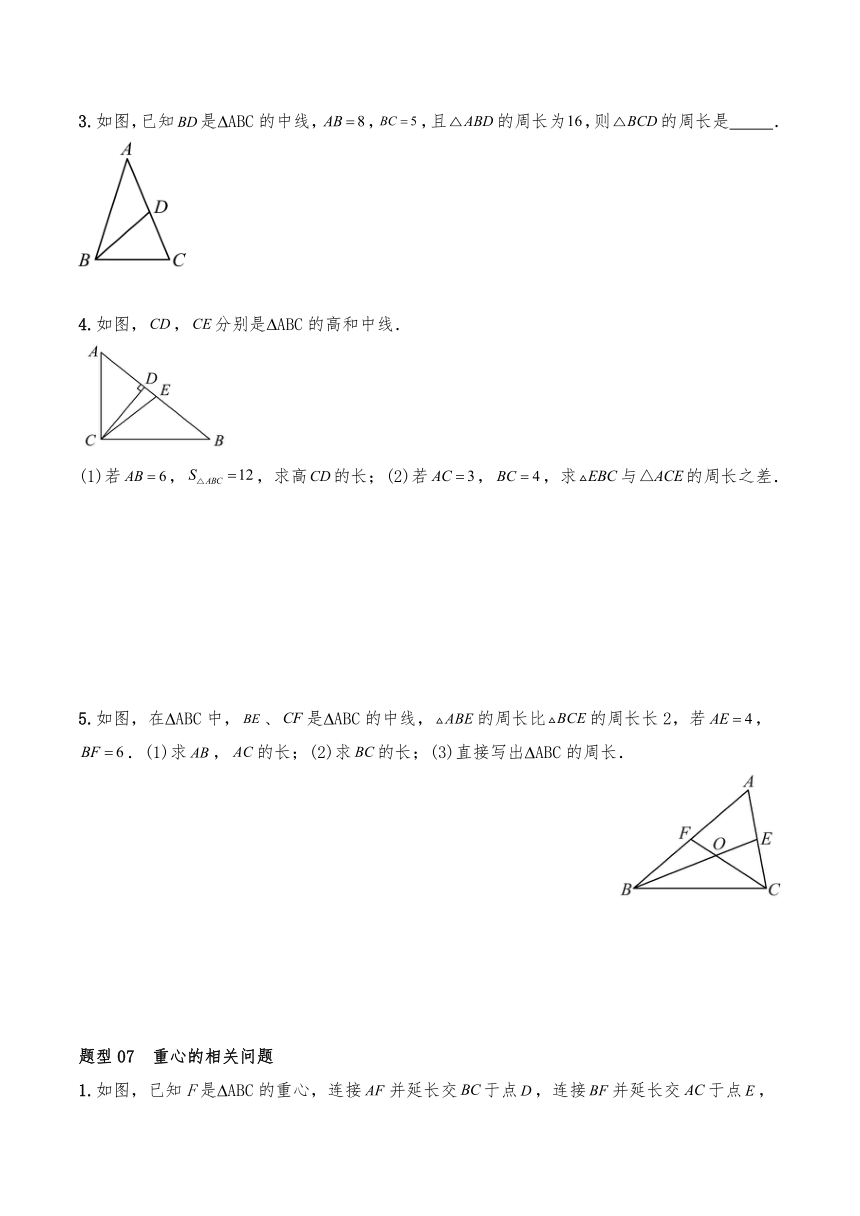
3.如图,已知是 ABC的中线,,,且的周长为,则的周长是 .
4.如图,,分别是 ABC的高和中线.
(1)若,,求高的长;(2)若,,求与的周长之差.
5.如图,在 ABC中,、是 ABC的中线,的周长比的周长长2,若,.(1)求,的长;(2)求的长;(3)直接写出 ABC的周长.
题型07 重心的相关问题
1.如图,已知F是 ABC的重心,连接并延长交于点,连接并延长交于点,记面积为,四边形面积为,则与的大小关系是( )
A. B. C. D.无法确定
2.如图所示的网格由边长相同的小正方形组成,点在小正方形的顶点上,则 ABC的重心是( )
A.点 B.点 C.点 D.点
3.如图,点是 ABC的重心,连接并延长,交边于点.若,则( )
A.2 B. C. D.
4. ABC的顶点都在正方形网格格点(图中网格线的交点)上,每个小正方形边长为1.请借助网格和无刻度直尺按要求作图.
(1)在图①中,作出 ABC的中线;(2)在图②中,作出 ABC的重心,记为点.
5.【发现与探究】三角形的重心
三角形三条中线的交点叫三角形的重心.重心是个物理名词.从效果上看,我们可以认为物体所受重力的合力集中于一点,这一点叫物体的重心.图1中,如果取一块均匀的三角形纸板,用一根细线绳从重心处将三角形提起来,纸板就会处于水平状态.为什么会平衡呢?希望你经过下面的探索过程能得到答案.图2中,是的中线,与等底等高,面积相等,记作.图3中,若三条中线、、交于点,则是的中线,利用上述结论可得:,同理,.
(1)图3中,若设,,,猜想,,之间的数量关系,并证明你的猜想;
(2)由(1)可知被三条中线分成的六个三角形面积 ,如果面积为,用含有的式子表示的面积为 ,: ;
(3)图4中,是重心,点、在的边、上,、交于,,,,求四边形的面积.
题型8画三角形的高线
1.如图,已知,根据下列要求作图并回答问题:
(1)作边上的高;(2)过点作直线的垂线,垂足为;(3)点到直线的距离是线段_______的长度;(4)线段的长度表示点_____到直线_______的距离.(不要求写画法,只需写出结论即可)
2.下列能表示 ABC的边上的高的是( )
A. B. C.D.
3.在 ABC中,作边上的高,正确的是( )
A. B. C. D.
4.如图,已知 ABC,根据下列要求画出图形并回答问题:
(1)作边上的高;(2)过点画的垂线,垂足为;(3)过点画的平行线,交于点;(4)点到直线的距离是线段___________的长度.
题型09 与高线相关的计算
1.如图,在 ABC中,,,垂足分别为,,与交于点,连接并延长交于点若,,,则( )
A. B. C. D.
2.如图,在 ABC中,,,为边上的高,平分,交于点,交于点,则的大小为( )
A. B. C. D.
3.在 ABC中,为边上的高,,,则
4.(1)如图1,在中,,,,,于点D,求的长;
(2)如图2,在 ABC中,,,求 ABC的高与的比;
(3)如图3,在 ABC中,,点,分别在边,上,且,,,垂足分别为点,.若,求的值.
5.【图形定义】有一条高线相等的两个三角形称为等高三角形.
例如:如图①,在 ABC和中,分别是和边上的高线,且,则 ABC和是等高三角形.
【性质探究】如图①,用,分别表示 ABC和的面积.
则,∵,∴.
【性质应用】(1)如图②,D是 ABC的边上的一点.若,则__________;(直接写出答案)
(2)如图③,在 ABC中,D,E分别是和边上的点.若,,,则=__________,=_________;(直接写出答案)
(3)如图③,在 ABC中,D,E分别是和边上的点,若,,,请用含的式子表示的面积.
题型10 与角平分线相关的计算
1.如图,在 ABC中,,点在内部,且到三边的距离相等,则的度数为( )
A. B. C. D.
2.如图,是 ABC的角平分线,是的角平分线,若,则的度数是 .
3.如图,是的平分线,是的平分线,与交于若,,则的度数为 .
4.如图,在中,度,与的平分线交于点,则∠= ;∠与∠的平分线交于点,得∠;……∠与的平分线交于点,得∠.则∠= °
5.如图,在 ABC中,已知,点O为 ABC内一点,且,其中平分,平分,平分,平分平分,平分,…,以此类推,则 , .
题型11 三角形中的“三线”相关角度运算
1.如图,在 ABC中,AD平分交BC于点D,AE是BC边上的高,,则的度数为 .
2.在 ABC中,为的平分线,为边上的高.若,,则 度.
3.如图,是 ABC的角平分线,是 ABC的高,,,点为边上一点,当 BDF为直角三角形时,则的度为 .
4.如图,在 ABC中,平分,交于点,为边上的高.(1)若,,求的度数;(2)在(1)的条件下,求的度数;
(3)若,直接写出、、的关系.
题型12 三角形中的“三线”相关综合运算
1.如图,,,分别是 ABC的高、角平分线、中线,则下列各式中错误的是( )
A. B. C. D.
2.如图,、分别是 ABC的高线和中线.若 ABC的面积为12,,则的长为( )
A.4 B.3 C. D.
3.如图,分别是 ABC的高线、中线,若,则高线长为( )
A.2 B.4 C.6 D.8
4.如图,在 ABC中,,分别是 ABC的中线和高,是的角平分线.(1)若 ABC的面积为,,求的长;(2)若,,求的大小.
参考答案
题型01 确定三角形的条件
1.D
【详解】A.由于,则本选项中的三条线段不能组成三角形,不符合题意;
B.由于,则本选项中的三条线段不能组成三角形,不符合题意;
C.由于,则本选项中的三条线段不能组成三角形,不符合题意;
D.由于,则本选项中的三条线段能组成三角形,符合题意.故选:D.
2.D
【详解】解:A、因为,所以长度为2,4,8的三条线段不能组成三角形;
B、因为,所以长度为5,5,10的三条线段不能组成三角形;
C、因为,所以长度为2,10,13的三条线段不能组成三角形;
D、因为,所以长度为3,6,8的三条线段能组成三角形;故选:D.
3.C
【详解】A、3,4,7,∵,∴3,4,7的三根小木棒首尾顺次相接,不能摆成三角形;
B、6,8,15,∵,∴6,8,15的三根小木棒首尾顺次相接,不能摆成三角形;
C、5,12,13,∵,∴5,12,13的三根小木棒首尾顺次相接,能摆成三角形;
D、5,5,11,∵,∴5,5,11的三根小木棒首尾顺次相接,不能摆成三角形.故选:C.
4.D
【详解】解:A、由,此选项不符合题意;B、由,此选项不符合题意;
C、由,此选项不符合题意;D、由,此选项符合题意;故选:D.
题型02 求三角形第三边的取值范围
1.
【详解】解:依题意,
根据三边关系可得解得: 故答案为:.
2.
【详解】解:∵,,∴;故答案为:.
3.
【详解】解:∵三角形的三边长分别为,,8,
∴,解得:,
∵为正整数,∴的值为,,,,,
∴满足条件的值的和为,故答案为:.
题型03 根据三角形的三边关系求值
1.
【详解】解:三角形的两边长分别是和,设第三边的长为,,即,
为奇数,,该三角形的周长,故答案为:.
2.11或13
【详解】解:根据三角形三边关系可得,即,
∵边长为偶数,∴或,∴当时,三角形的周长为,
当时,三角形的周长为,故答案为:11或13.
3.C
【详解】解:设三角形的第三边长是,
由三角形三边关系定理得:,,
第三边长取到10,,,
能使得第三边长取到10的最小正整数是.故选:C.
4.A
【详解】解:设第三边的长度为,则即,
又因为周长是偶数并且是7的倍数,所以x为偶数,
当时,周长为,不是7的倍数,
但时,周长为,是7的倍数,故选:A.
题型04 三角形的三边关系的实际运用
1.A
【详解】解:三角形两边之和大于第三边,两根长度分别为和的细木条做一个三角形的框架,可以把的细木条分为两截.理由:,满足两边之和大于第三边.故选:A.
2.B
【详解】解:设三角形框架的第三边长为x,根据题意,可得 ,即,
故选项A、C、D不符合题意,选项B符合题意.故选:B.
3.A
【详解】解:、、是的三边的长,,,,
原式.故选:A.
4.解:不合理,理由:由题意得圆规先生的两腿与它所画的圆的一条半径组成一个三角形,设所画的圆的一条半径为,根据三角形三边关系定理得,即,,,即圆规先生不能画出半径为的圆.
5.证明:在中,,
在中,,
在中,,
在 ABC中,,
,
,
,
与的和小于四边形的周长.
题型05 中线平分三角形的面积
1.B
【详解】解:如图,连接、、;
,,,,
,同理可得,, ,
;故选:B
2.A
【详解】解:∵是的 ABC的中线,且 ABC的面积为12,∴,
又∵是的的中线,∴,故选:A.
3.B
【详解】解:,且点是的中点,.
点是的中点,.点为的中点,.故选:B.
4.C
【详解】解:如图,连接.∵点D是的中点,,∴,
∵,∴,
∵,∴,∴,
∵点D是的中点,∴.故选:C.
5.D
【详解】解:如图,连接,过点作于点,过点作于点,
,,,,
,,
,,
,,同理可得:,
,同理可得:,
依此类推:. 故选:D.
题型06 中线中的周长差与边的差
1.
【详解】解:∵是 ABC的中线,∴,
∴的周长的周长,故答案为:.
2.A
【详解】解:的周长为,∴,
∵是边上的中线,∴,则,∴,
∵的周长为,的周长为,
∴,
∴与的周长之差为,故选:A .
3.
【详解】解:是 ABC的中线,,
的周长为,即,,
的周长.故答案为:.
4.(1),,
,解得,高的长为4.
(2)的中线是,,
与的周长之差为:.
5.(1)解:∵分别是边上的中线,∴点分别为的中点.
∵,,∴,.
(2)解:∵的周长比的周长长2,
∴,由(1)得,∴,
(3)解: 由(1)(2)得,,,∴的周长为:.
题型07 重心的相关问题
1.A
【详解】解:∵F是 ABC的重心,∴
∴,∴;故选:A.
2.A
【详解】解:由图可知,直线经过 ABC的边上的中点,直线经过的边上的中点,
∴点是 ABC重心,故选:.
3.C
【详解】解:∵点是 ABC的重心,∴点为的中点,∴,∴,故选:C.
4.(1)解:如图,点为所求作点.
(2)如图,点为所求作点
5.(1)解: 由题意可知,,,
,, ,
,, ,.
(2)由(1)可知被三条中线分成的六个三角形面积相等,每个小三角形的面积是大三角形面积的,所以的面积为.∵∴,即故答案为;相等,; .
(3)解:是的重心,,
,,
.
题型8画三角形的高线
1.(1)解:如下图所示,线段即为边上的高;
(2)解:如下图所示,
(3)解:点到直线的距离是线段的长度,故答案为:;
(4)解:线段的长度表示点到直线的距离,故答案为:,;
2.B
【详解】解:A.不是任何边上的高,故不符合题意;B.是任何边上的高,故符合题意;
C.是任何边上的高,故不符合题意;D.不是任何边上的高,故不符合题意;故选B.
3.D
【详解】解:根据三角形高线的定义,边上的高是过点B向作垂线垂足为E,
纵观各图形,D选项符合高线的定义,故选:D.
4.(1)解:如图所示,过点C作交延长线于D,则即为所求;
(2)解:如图所示,即为所求;
(3)解:如图所示,即为所求;
(4)解:∵,∴,∴点到直线的距离是线段的长度.
题型09 与高线相关的计算
1.B
【详解】解:∵,,与交于点,
∴(三角形三条高所在的直线交于一点),∵,
∵,,,∴,∴,故选B.
2.C
【详解】解:∵,,
∵平分,,
∵为边上的高,,,,故选:C.
3.或
【详解】解:如图1,∵为边上的高,∴,
又∵,∴,∴;
如图2,∵为边上的高,∴,
又∵∴,
∴;故答案为:或.
4.(1)解:,,;
(2)解:,,,;
(3)解:,,,
,,
又,,即.
5.(1)解:∵是等高三角形,∴;故答案为:;
(2)解:∵,,∴,∴;
∵,∴,∴;故答案为:;
(3)解:∵,,∴,∴;
∵,∴,∴;
题型10 与角平分线相关的计算
1.C
【详解】解:点在 ABC内部,且到三边的距离相等,
平分,平分,,,
,,
,,故选:C.
2.
【详解】解:是 ABC的角平分线,,,
是的角平分线,,故答案为:.
3.
【详解】解:如图,连接,,,
,,
是的平分线,是的平分线,
,,,
,故答案为:.
4.
【详解】解:∵是的平分线,是的平分线,∴,,
又∵,,∴,∴,
∵,∴;同理可得,……∴,∴,故答案为:;
5.
【详解】解:,,
,,,
平分,平分,,,
,,
,,,,
同理可得:,,
,,
,,,
归纳类推得:,其中为正整数,
∴,故答案为:;.
题型11 三角形中的“三线”相关角度运算
1.9
【详解】解:∵平分交于点D,于点E,∴,,
∵∴,∴,∵,∴.故答案为:9
2.20或60
【详解】解:∵为边上的高,∴,
∵,∴,分以下两种情况:
如图,当点E在点D左边时,∵,∴,
∵是平分线,∴,
∴;
如图,当点E在点D右边时,∵,∴,
∵是平分线,∴,
∴.故答案为:20或60.
3.或
【详解】解:如图:当时,
∵是 ABC的角平分线,,∴,
∴中,;
如图∶当时,同理可得,
∵,∴,
∴.综上所述:的度数为或.故答案为:或.
4.(1)解:在 ABC中,,,;
又是的平分线,;
(2)解:是边上的高,,
在中,,,,
由(1)知,,,即;
(3)解:,理由如下:
且是的平分线,,
,.
题型12 三角形中的“三线”相关综合运算
1.C
【详解】解:∵,,分别是 ABC的高、角平分线、中线,
∴,,.
结合选项可知,A、B、D选项不符合题意,C选项符合题意;故选:C.
2.D
【详解】解:∵是 ABC的中线, ABC的面积为 12 ,,
∵是 ABC的高线,,∴,则,故选:D.
3.B
【详解】解:∵是 ABC的中线,,∴,
∵是 ABC的高线,∴,即,解得,故选:B.
4.(1)解:是 ABC的中线, ABC的面积为,,,
,,;
(2),,,
是的角平分线,,是 ABC的高,,
,.
题型01 确定三角形的条件
1.以下列各组数为边,能组成三角形的是( )
A. B. C. D.
2.下列长度的线段能组成三角形的是( )
A.2,4,8 B.5,5,10 C.2,10,13 D.3,6,8
3.下列每组数分别是三根小木棒的长度,将它们首尾顺次相接,能摆成三角形的是( )
A.3,4,7 B.6,8,15 C.5,12,13 D.5,5,11
4.将周长为的三角形的三条边依次放在一条直线上,其中所标数据正确的是( )
A. B.
C. D.
题型02 求三角形第三边的取值范围
1.等腰三角形的周长为16厘米,腰长为厘米,底边长为厘米,其中的取值范围是 .
2.已知 ABC的三边长为a、b、c,其中,则边长c的取值范围是 .
3.已知某三角形的三边长分别为,,,其中为正整数,则满足条件的值的和为 .
题型03 根据三角形的三边关系求值
1.已知三角形的两边长分别是和,选一个你喜欢的奇数作第三边,则该三角形的周长是 .
2.一个三角形的两边长分别是2和5,另一边长为偶数,则这个三角形的周长为 .
3.已知 ABC的两边长分别为2和,则能使得第三边长取到10的最小正整数是( )
A.5 B.6 C.7 D.8
4.三角形的两边长分别是、,周长是偶数并且是7的倍数,则第三边的长度是( )
A. B. C. D.
题型04 三角形的三边关系的实际运用
1.若使用如图所示的、两根直铁丝做成一个三角形框架,需要将其中一根铁丝折成两段,则可以分为两段的铁丝是( )
A.只有可以 B.只有可以 C.,都可以 D.,都不可以
2.一木工师傅有两根长分别为的木条,他要找第三根木条,将它们钉成一个三角形框架,以下4根木条,他选择( )的木条合适.
A.3cm B. C. D.
3.已知、、是的三边长,则( )
A. B. C. D.
4.某天,所有文具聚在一起开了个茶话会,圆规先生的话引起了大家的热议,你觉得圆规先生的话合理吗?如果不合理,请说明理由.
5.已知,如图四边形中,是与的交点,试说明:与的和小于四边形的周长.
题型05 中线平分三角形的面积
1.如图,已知 ABC的面积为,分别延长至点,使,延长至点,使,延长至点,使,依次连接,,,则阴影部分的面积为( )
A. B. C. D.
2.如图,是 ABC的中线,是的中线,若 ABC的面积为12,则的面积为( )
A.3 B.4 C.6 D.8
3.如图所示,在 ABC中,D、E、F分别为的中点,且,则的面积等于( )
A. B. C. D.
4.如图,在 ABC中,点D是的中点,连接,点E在上,且,于点F.若,,则 ABC的面积为( )
A.50 B.55 C.60 D.65
5.如图,对面积为的 ABC逐次进行以下操作:第一次操作,分别延长、、至点、、,使得,,,顺次连接、、,得到,记其面积为;第二次操作,分别延长、、至点、、,使得,,,顺次连接、、,得到,记其面积为;…; 按此规律继续下去,可得到 A5B5C5,则其面积为 ( )
A. B. C. D.
题型06 中线中的周长差与边的差
1.如图, ABC中,,,是 ABC的中线,则的周长比的周长大 .
2.如图, ABC的周长是,是边上的中线,,,则与的周长之差为( )
A.2 B.3 C.4 D.6
3.如图,已知是 ABC的中线,,,且的周长为,则的周长是 .
4.如图,,分别是 ABC的高和中线.
(1)若,,求高的长;(2)若,,求与的周长之差.
5.如图,在 ABC中,、是 ABC的中线,的周长比的周长长2,若,.(1)求,的长;(2)求的长;(3)直接写出 ABC的周长.
题型07 重心的相关问题
1.如图,已知F是 ABC的重心,连接并延长交于点,连接并延长交于点,记面积为,四边形面积为,则与的大小关系是( )
A. B. C. D.无法确定
2.如图所示的网格由边长相同的小正方形组成,点在小正方形的顶点上,则 ABC的重心是( )
A.点 B.点 C.点 D.点
3.如图,点是 ABC的重心,连接并延长,交边于点.若,则( )
A.2 B. C. D.
4. ABC的顶点都在正方形网格格点(图中网格线的交点)上,每个小正方形边长为1.请借助网格和无刻度直尺按要求作图.
(1)在图①中,作出 ABC的中线;(2)在图②中,作出 ABC的重心,记为点.
5.【发现与探究】三角形的重心
三角形三条中线的交点叫三角形的重心.重心是个物理名词.从效果上看,我们可以认为物体所受重力的合力集中于一点,这一点叫物体的重心.图1中,如果取一块均匀的三角形纸板,用一根细线绳从重心处将三角形提起来,纸板就会处于水平状态.为什么会平衡呢?希望你经过下面的探索过程能得到答案.图2中,是的中线,与等底等高,面积相等,记作.图3中,若三条中线、、交于点,则是的中线,利用上述结论可得:,同理,.
(1)图3中,若设,,,猜想,,之间的数量关系,并证明你的猜想;
(2)由(1)可知被三条中线分成的六个三角形面积 ,如果面积为,用含有的式子表示的面积为 ,: ;
(3)图4中,是重心,点、在的边、上,、交于,,,,求四边形的面积.
题型8画三角形的高线
1.如图,已知,根据下列要求作图并回答问题:
(1)作边上的高;(2)过点作直线的垂线,垂足为;(3)点到直线的距离是线段_______的长度;(4)线段的长度表示点_____到直线_______的距离.(不要求写画法,只需写出结论即可)
2.下列能表示 ABC的边上的高的是( )
A. B. C.D.
3.在 ABC中,作边上的高,正确的是( )
A. B. C. D.
4.如图,已知 ABC,根据下列要求画出图形并回答问题:
(1)作边上的高;(2)过点画的垂线,垂足为;(3)过点画的平行线,交于点;(4)点到直线的距离是线段___________的长度.
题型09 与高线相关的计算
1.如图,在 ABC中,,,垂足分别为,,与交于点,连接并延长交于点若,,,则( )
A. B. C. D.
2.如图,在 ABC中,,,为边上的高,平分,交于点,交于点,则的大小为( )
A. B. C. D.
3.在 ABC中,为边上的高,,,则
4.(1)如图1,在中,,,,,于点D,求的长;
(2)如图2,在 ABC中,,,求 ABC的高与的比;
(3)如图3,在 ABC中,,点,分别在边,上,且,,,垂足分别为点,.若,求的值.
5.【图形定义】有一条高线相等的两个三角形称为等高三角形.
例如:如图①,在 ABC和中,分别是和边上的高线,且,则 ABC和是等高三角形.
【性质探究】如图①,用,分别表示 ABC和的面积.
则,∵,∴.
【性质应用】(1)如图②,D是 ABC的边上的一点.若,则__________;(直接写出答案)
(2)如图③,在 ABC中,D,E分别是和边上的点.若,,,则=__________,=_________;(直接写出答案)
(3)如图③,在 ABC中,D,E分别是和边上的点,若,,,请用含的式子表示的面积.
题型10 与角平分线相关的计算
1.如图,在 ABC中,,点在内部,且到三边的距离相等,则的度数为( )
A. B. C. D.
2.如图,是 ABC的角平分线,是的角平分线,若,则的度数是 .
3.如图,是的平分线,是的平分线,与交于若,,则的度数为 .
4.如图,在中,度,与的平分线交于点,则∠= ;∠与∠的平分线交于点,得∠;……∠与的平分线交于点,得∠.则∠= °
5.如图,在 ABC中,已知,点O为 ABC内一点,且,其中平分,平分,平分,平分平分,平分,…,以此类推,则 , .
题型11 三角形中的“三线”相关角度运算
1.如图,在 ABC中,AD平分交BC于点D,AE是BC边上的高,,则的度数为 .
2.在 ABC中,为的平分线,为边上的高.若,,则 度.
3.如图,是 ABC的角平分线,是 ABC的高,,,点为边上一点,当 BDF为直角三角形时,则的度为 .
4.如图,在 ABC中,平分,交于点,为边上的高.(1)若,,求的度数;(2)在(1)的条件下,求的度数;
(3)若,直接写出、、的关系.
题型12 三角形中的“三线”相关综合运算
1.如图,,,分别是 ABC的高、角平分线、中线,则下列各式中错误的是( )
A. B. C. D.
2.如图,、分别是 ABC的高线和中线.若 ABC的面积为12,,则的长为( )
A.4 B.3 C. D.
3.如图,分别是 ABC的高线、中线,若,则高线长为( )
A.2 B.4 C.6 D.8
4.如图,在 ABC中,,分别是 ABC的中线和高,是的角平分线.(1)若 ABC的面积为,,求的长;(2)若,,求的大小.
参考答案
题型01 确定三角形的条件
1.D
【详解】A.由于,则本选项中的三条线段不能组成三角形,不符合题意;
B.由于,则本选项中的三条线段不能组成三角形,不符合题意;
C.由于,则本选项中的三条线段不能组成三角形,不符合题意;
D.由于,则本选项中的三条线段能组成三角形,符合题意.故选:D.
2.D
【详解】解:A、因为,所以长度为2,4,8的三条线段不能组成三角形;
B、因为,所以长度为5,5,10的三条线段不能组成三角形;
C、因为,所以长度为2,10,13的三条线段不能组成三角形;
D、因为,所以长度为3,6,8的三条线段能组成三角形;故选:D.
3.C
【详解】A、3,4,7,∵,∴3,4,7的三根小木棒首尾顺次相接,不能摆成三角形;
B、6,8,15,∵,∴6,8,15的三根小木棒首尾顺次相接,不能摆成三角形;
C、5,12,13,∵,∴5,12,13的三根小木棒首尾顺次相接,能摆成三角形;
D、5,5,11,∵,∴5,5,11的三根小木棒首尾顺次相接,不能摆成三角形.故选:C.
4.D
【详解】解:A、由,此选项不符合题意;B、由,此选项不符合题意;
C、由,此选项不符合题意;D、由,此选项符合题意;故选:D.
题型02 求三角形第三边的取值范围
1.
【详解】解:依题意,
根据三边关系可得解得: 故答案为:.
2.
【详解】解:∵,,∴;故答案为:.
3.
【详解】解:∵三角形的三边长分别为,,8,
∴,解得:,
∵为正整数,∴的值为,,,,,
∴满足条件的值的和为,故答案为:.
题型03 根据三角形的三边关系求值
1.
【详解】解:三角形的两边长分别是和,设第三边的长为,,即,
为奇数,,该三角形的周长,故答案为:.
2.11或13
【详解】解:根据三角形三边关系可得,即,
∵边长为偶数,∴或,∴当时,三角形的周长为,
当时,三角形的周长为,故答案为:11或13.
3.C
【详解】解:设三角形的第三边长是,
由三角形三边关系定理得:,,
第三边长取到10,,,
能使得第三边长取到10的最小正整数是.故选:C.
4.A
【详解】解:设第三边的长度为,则即,
又因为周长是偶数并且是7的倍数,所以x为偶数,
当时,周长为,不是7的倍数,
但时,周长为,是7的倍数,故选:A.
题型04 三角形的三边关系的实际运用
1.A
【详解】解:三角形两边之和大于第三边,两根长度分别为和的细木条做一个三角形的框架,可以把的细木条分为两截.理由:,满足两边之和大于第三边.故选:A.
2.B
【详解】解:设三角形框架的第三边长为x,根据题意,可得 ,即,
故选项A、C、D不符合题意,选项B符合题意.故选:B.
3.A
【详解】解:、、是的三边的长,,,,
原式.故选:A.
4.解:不合理,理由:由题意得圆规先生的两腿与它所画的圆的一条半径组成一个三角形,设所画的圆的一条半径为,根据三角形三边关系定理得,即,,,即圆规先生不能画出半径为的圆.
5.证明:在中,,
在中,,
在中,,
在 ABC中,,
,
,
,
与的和小于四边形的周长.
题型05 中线平分三角形的面积
1.B
【详解】解:如图,连接、、;
,,,,
,同理可得,, ,
;故选:B
2.A
【详解】解:∵是的 ABC的中线,且 ABC的面积为12,∴,
又∵是的的中线,∴,故选:A.
3.B
【详解】解:,且点是的中点,.
点是的中点,.点为的中点,.故选:B.
4.C
【详解】解:如图,连接.∵点D是的中点,,∴,
∵,∴,
∵,∴,∴,
∵点D是的中点,∴.故选:C.
5.D
【详解】解:如图,连接,过点作于点,过点作于点,
,,,,
,,
,,
,,同理可得:,
,同理可得:,
依此类推:. 故选:D.
题型06 中线中的周长差与边的差
1.
【详解】解:∵是 ABC的中线,∴,
∴的周长的周长,故答案为:.
2.A
【详解】解:的周长为,∴,
∵是边上的中线,∴,则,∴,
∵的周长为,的周长为,
∴,
∴与的周长之差为,故选:A .
3.
【详解】解:是 ABC的中线,,
的周长为,即,,
的周长.故答案为:.
4.(1),,
,解得,高的长为4.
(2)的中线是,,
与的周长之差为:.
5.(1)解:∵分别是边上的中线,∴点分别为的中点.
∵,,∴,.
(2)解:∵的周长比的周长长2,
∴,由(1)得,∴,
(3)解: 由(1)(2)得,,,∴的周长为:.
题型07 重心的相关问题
1.A
【详解】解:∵F是 ABC的重心,∴
∴,∴;故选:A.
2.A
【详解】解:由图可知,直线经过 ABC的边上的中点,直线经过的边上的中点,
∴点是 ABC重心,故选:.
3.C
【详解】解:∵点是 ABC的重心,∴点为的中点,∴,∴,故选:C.
4.(1)解:如图,点为所求作点.
(2)如图,点为所求作点
5.(1)解: 由题意可知,,,
,, ,
,, ,.
(2)由(1)可知被三条中线分成的六个三角形面积相等,每个小三角形的面积是大三角形面积的,所以的面积为.∵∴,即故答案为;相等,; .
(3)解:是的重心,,
,,
.
题型8画三角形的高线
1.(1)解:如下图所示,线段即为边上的高;
(2)解:如下图所示,
(3)解:点到直线的距离是线段的长度,故答案为:;
(4)解:线段的长度表示点到直线的距离,故答案为:,;
2.B
【详解】解:A.不是任何边上的高,故不符合题意;B.是任何边上的高,故符合题意;
C.是任何边上的高,故不符合题意;D.不是任何边上的高,故不符合题意;故选B.
3.D
【详解】解:根据三角形高线的定义,边上的高是过点B向作垂线垂足为E,
纵观各图形,D选项符合高线的定义,故选:D.
4.(1)解:如图所示,过点C作交延长线于D,则即为所求;
(2)解:如图所示,即为所求;
(3)解:如图所示,即为所求;
(4)解:∵,∴,∴点到直线的距离是线段的长度.
题型09 与高线相关的计算
1.B
【详解】解:∵,,与交于点,
∴(三角形三条高所在的直线交于一点),∵,
∵,,,∴,∴,故选B.
2.C
【详解】解:∵,,
∵平分,,
∵为边上的高,,,,故选:C.
3.或
【详解】解:如图1,∵为边上的高,∴,
又∵,∴,∴;
如图2,∵为边上的高,∴,
又∵∴,
∴;故答案为:或.
4.(1)解:,,;
(2)解:,,,;
(3)解:,,,
,,
又,,即.
5.(1)解:∵是等高三角形,∴;故答案为:;
(2)解:∵,,∴,∴;
∵,∴,∴;故答案为:;
(3)解:∵,,∴,∴;
∵,∴,∴;
题型10 与角平分线相关的计算
1.C
【详解】解:点在 ABC内部,且到三边的距离相等,
平分,平分,,,
,,
,,故选:C.
2.
【详解】解:是 ABC的角平分线,,,
是的角平分线,,故答案为:.
3.
【详解】解:如图,连接,,,
,,
是的平分线,是的平分线,
,,,
,故答案为:.
4.
【详解】解:∵是的平分线,是的平分线,∴,,
又∵,,∴,∴,
∵,∴;同理可得,……∴,∴,故答案为:;
5.
【详解】解:,,
,,,
平分,平分,,,
,,
,,,,
同理可得:,,
,,
,,,
归纳类推得:,其中为正整数,
∴,故答案为:;.
题型11 三角形中的“三线”相关角度运算
1.9
【详解】解:∵平分交于点D,于点E,∴,,
∵∴,∴,∵,∴.故答案为:9
2.20或60
【详解】解:∵为边上的高,∴,
∵,∴,分以下两种情况:
如图,当点E在点D左边时,∵,∴,
∵是平分线,∴,
∴;
如图,当点E在点D右边时,∵,∴,
∵是平分线,∴,
∴.故答案为:20或60.
3.或
【详解】解:如图:当时,
∵是 ABC的角平分线,,∴,
∴中,;
如图∶当时,同理可得,
∵,∴,
∴.综上所述:的度数为或.故答案为:或.
4.(1)解:在 ABC中,,,;
又是的平分线,;
(2)解:是边上的高,,
在中,,,,
由(1)知,,,即;
(3)解:,理由如下:
且是的平分线,,
,.
题型12 三角形中的“三线”相关综合运算
1.C
【详解】解:∵,,分别是 ABC的高、角平分线、中线,
∴,,.
结合选项可知,A、B、D选项不符合题意,C选项符合题意;故选:C.
2.D
【详解】解:∵是 ABC的中线, ABC的面积为 12 ,,
∵是 ABC的高线,,∴,则,故选:D.
3.B
【详解】解:∵是 ABC的中线,,∴,
∵是 ABC的高线,∴,即,解得,故选:B.
4.(1)解:是 ABC的中线, ABC的面积为,,,
,,;
(2),,,
是的角平分线,,是 ABC的高,,
,.
同课章节目录
