第一章《三角形》复习题--七大重要的三角形全等模型(含详解)--苏科版八年级数学上册
文档属性
| 名称 | 第一章《三角形》复习题--七大重要的三角形全等模型(含详解)--苏科版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-06 05:57:18 | ||
图片预览




文档简介
第一章《三角形》复习题--七大重要的三角形全等模型
题型一:倍长中线
1.综合与实践:小明遇到这样一个问题,如图1,中,,,点为的中点,求的取值范围.
小明发现老师讲过的“倍长中线法”可以解决这个问题,所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法,他的做法是:如图2,延长到,使,连接,构造,经过推理和计算使问题得到解决
请回答:(1)小明证明用到的判定定理是:________;(填入你选择的选项字母)
A. B. C. D.
(2)的取值范围是________.
小明还发现:倍长中线法最重要的一点就是延长中线一倍,完成全等三角形模型的构造.
参考小明思考问题的方法,解决问题:
如图3,在正方形中,为边的中点,、分别为,边上的点,若,,,求的长.
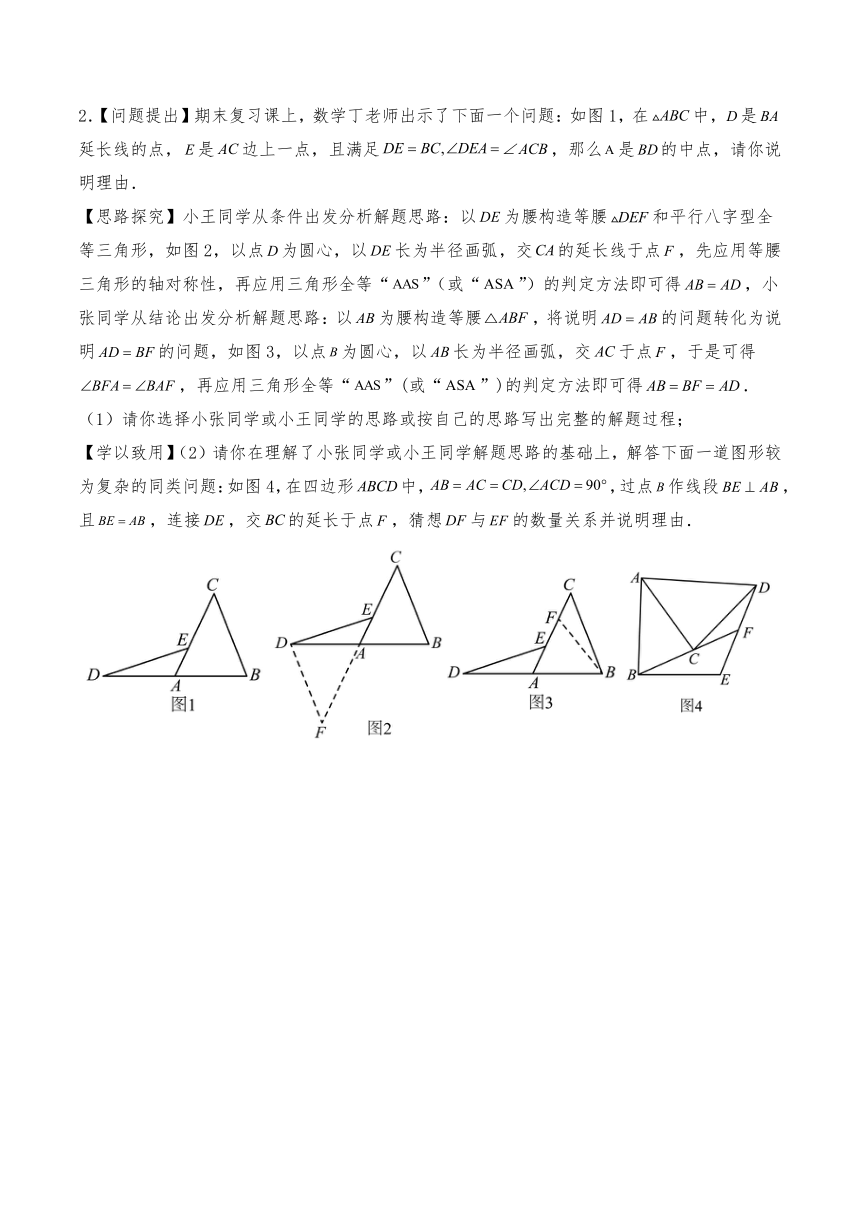
2.【问题提出】期末复习课上,数学丁老师出示了下面一个问题:如图1,在中,是延长线的点,是边上一点,且满足,那么是的中点,请你说明理由.
【思路探究】小王同学从条件出发分析解题思路:以为腰构造等腰和平行八字型全等三角形,如图2,以点为圆心,以长为半径画弧,交的延长线于点,先应用等腰三角形的轴对称性,再应用三角形全等“”(或“”)的判定方法即可得,小张同学从结论出发分析解题思路:以为腰构造等腰,将说明的问题转化为说明的问题,如图3,以点为圆心,以长为半径画弧,交于点,于是可得,再应用三角形全等“”(或“”)的判定方法即可得.
(1)请你选择小张同学或小王同学的思路或按自己的思路写出完整的解题过程;
【学以致用】(2)请你在理解了小张同学或小王同学解题思路的基础上,解答下面一道图形较为复杂的同类问题:如图4,在四边形中,,过点作线段,且,连接,交的延长于点,猜想与的数量关系并说明理由.
3.【问题情境】课外兴趣小组活动时,老师提出了如下问题:
如图①,△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB,依据是 .A.SAS;B. SSS;C. AAS;D. HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
(3)【初步运用】如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AC=BF.求证AE=FE.
4.阅读材料:如图1,在中,D,E分别是边AB,AC的中点,小亮在证明“三角形的中位线平行于第三边,且等于第三边的一半”时,通过延长DE到点F,使,连接CF,证明,再证四边形DBCF是平行四边形即得证.
类比迁移:(1)如图2,AD是的中线,E是AC上的一点,BE交AD于点F,且,求证:.
小亮发现可以类比材料中的思路进行证明.
证明:如图2,延长AD至点M,使,连接MC,……
请根据小亮的思路完成证明过程.
方法运用:(2)如图3,在等边中,D是射线BC上一动点(点D在点C的右侧),连接AD.把线段CD绕点D逆时针旋转120°得到线段DE,F是线段BE的中点,连接DF、CF.请你判断线段DF与AD的数量关系,并给出证明.
5.阅读与思考:下面是小宇同学的数学日记,请仔细阅读,并完成相应的任务.
“倍长中线法”中线是三角形中的重要线段之一,利用中线解决几何问题时,常常采用“倍长中线法”加辅助线. 如图1.在中,平分,且恰好是边的中点.求证:. 证明:如图2,延长至点,使.∵是边的中点 ∴. ∵,,∴(依据).∴. ∵平分,∴,∴,∴,∴.
任务:(1)材料中的“依据”是________.(填选项)
A. B. C. D.
(2)在中,,,则边上的中线长度的取值范围是________.(3)如图3,在四边形中,,平分,且是的中点,,,求的长.
题型二:截长补短模型
6.【方法探究】如图1,在中,平分,,探究,,之间的数量关系;
嘉铭同学通过思考发现,可以通过“截长、补短”两种方法解决问题:
方法1:如图2,在上截取,使得,连接,可以得到全等三角形,进而解决此问题.
方法2:如图3,延长到点,使得 ,连接,可以得到等腰三角形,进而解决此问题.
(1)根据探究,直接写出,,之间的数量关系;
【迁移应用】(2)如图4,在中,D是上一点,,,于,探究,,之间的数量关系,并证明.
【拓展延伸】(3)如图5,为等边三角形,点为延长线上一动点,连接.以为边在上方作等边,点是的中点,连接并延长,交的延长线于点.若,求证:.
7.(1)阅读理解:问题:如图1,在四边形中,对角线平分,.求证:.
思考:“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题.
方法1:在上截取,连接,得到全等三角形,进而解决问题;
方法2:延长到点,使得,连接,得到全等三角形,进而解决问题.
结合图1,在方法1和方法2中任选一种,添加辅助线并完成证明.
(2)问题解决:如图2,在(1)的条件下,连接,当时,探究线段,,之间的数量关系,并说明理由;
(3)问题拓展:如图3,在四边形中,,,过点作,垂足为点,请写出线段、、之间的数量关系.
8.李老师善于通过合适的主题整合教学内容,帮助同学们用整体的、联系的、发展的眼光看问题,形成科学的思维习惯,下面是李老师在“利用角的对称性构造全等模型”主题下设计的问题,请你解答.
(1)【观察发现】①如图1,是 ABC的角平分线,,在上截取,连接,则与的数量关系是__________;
②如图2, ABC的角平分线、相交于点P.当时,线段与的数量关系是__________;
(2)【探究迁移】如图3,在四边形中,,的平分线与的平分线恰好交于边上的点P,试判断与的数量关系,并说明理由.
9.【实际情境】手工课堂上,老师给每个制作小组发放一把花折伞和制作花折伞的材料及工具.同学们认真观察后,组装了花折伞的骨架,粘贴了彩色伞面,制作出精美的花折伞.
【模型建立】(1)如图1,从花折伞中抽象出“伞形图”.,.求证:.
【模型应用】(2)如图2,中,的平分线交于点.请你从以下两个条件:①;②中选择一个作为已知条件,另一个作为结论,并写出结论成立的证明过程.(注:只需选择一种情况作答)
10.阅读材料:截长补短法,是初中数学几何题中一种辅助线的添加方法.截长就是在长边上截取一条线段与某一短边相等,补短是通过在一条短边上延长一条线段与另一长边相等,从而解决问题.依据上述材料,解答下列问题:如图1,在 ABC中,平分,交于点,且,求证:.
(1)为了证明结论“”,小亮在上截取,使得,连接,解答了这个问题,请按照小亮的思路写证明过程;(提示:如果一个三角形有两个角相等,那么这两个角所对的边也相等)
(2)如图2,在四边形中,已知,,,,是的高,,,求的长.
题型三:一线三等角(K字型)模型
11.如图,中,,,为线段上一动点(不与点,重合),连接,作 ,交线段于,以下四个结论:
①;②当为中点时,;③当 ADE为等腰三角形时,;
④当时,.其中正确的结论的个数是( )
A. B. C. D.
12.如图,在中,,,点D为上一点,连接.过点B作于点E,过点C作交的延长线于点F.若,,则的长度为 .
13.(1)已知:如图①,在 ABC中,,,直线m经过点A,直线m,直线m,垂足分别为D,E.求证:.
(2)拓展:如图②,将(1)中的条件改为:在 ABC中,,D,A,E三点都在直线m上,并且有,其中为任意锐角或钝角:那么结论是否仍成立?若成立,请你给出证明;若不成立,请说明理由.
(3)应用,如图③,在 ABC中,是钝角,,,,直线m与的延长线交于点F,若, ABC的面积是15,求与的面积之和.
14.在 ABC中,,,直线经过点,且于,于.
(1)当直线绕点旋转到图1的位置时,求证:①;②;
(2)当直线绕点旋转到图2的位置时,求证:;
(3)当直线绕点旋转到图3的位置时,试问、、具有怎样的等量关系?请写出这个等量关系,并加以证明.
15.(1)如图①,,射线在这个角的内部,点B、C分别在的边、上,且,于点F,于点D.求证: ABD≌ CAF;
(2)如图②,点B、C分别在的边、上,点E、F都在内部的射线上,、分别是、 CAF的外角.已知,且.求证:;
(3)如图③,在 ABC中,,.点D在边上,,点E、F在线段上,.若 ABC的面积为17,求与 BDE的面积之和.
题型四:手拉手模型
16.已知:如图,分别以的边为腰向外作等腰直角、等腰直角,连接相交于点O,连接,①,②,③,④平分,⑤平分,则以上结论正确的有( )
A.①③⑤ B.②③④ C.③④⑤ D.①③④
17.如图1,等边与等边的顶点,,三点在一条直线上,连接交于点,连.(1)求证:;(2)求证:平分;
(3)设,若,直接写出a,b,c之间满足的数量关系.
18.如图,在 ABC中,为锐角,点D为直线上一动点,以为直角边且在的右侧作等腰直角三角形,,.
(1)如果,.①当点D在线段上时,如图1,线段、的位置关系为________,数量关系为________;②当点D在线段的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.(2)如图3,如果,,点D在线段上运动.探究:当多少度时,?请说明理由.
19.已知:△ABC与△BDE都是等腰三角形.BA=BC,BD=BE(AB>BD)且有∠ABC=∠DBE.(1)如图1,如果A、B、D在一直线上,且∠ABC=60°,求证:△BMN是等边三角形;(2)在第(1)问的情况下,直线AE和CD的夹角是 °;
(3)如图2,若A、B、D不在一直线上,但∠ABC=60°的条件不变则直线AE和CD的夹角是 °;
(4)如图3,若∠ACB=60°,直线AE和CD的夹角是 °.
20.【知识背景】我们在第十一章《三角形》中学习了三角形的边与角的性质,在第十二章《全等三角形》中学习了全等三角形的性质和判定,在第十三章《轴对称》中学习了等腰三角形的性质和判定.在一些探究题中经常用以上知识转化角和边,进而解决问题.
(1)【问题初探】如图(1),中,,,点D是BC上一点,连接AD,以AD为一边作 ADE,使,,连接BE,猜想BE和CD有怎样的数量关系,并说明理由.
(2)【类比再探】如图(2),中,,,点M是AB上一点,点D是BC上一点,连接MD,以MD为一边作,使,,连接BE,则______.(直接写出答案,不写过程;需要作辅助线的,请说明辅助线的作法,并在图(2)中作出辅助线)
(3)【方法迁移】如图(3),是等边三角形,点D是BC上一点,连接AD,以AD为一边作等边三角形ADE连接BE,则BD,BE,BC之间有怎样的数量关系?(直接写出答案,不写过程).
(4)【数学思考】如图(4),是等边三角形,点M是AB上一点,点D是BC上一点,连接MD,以MD为一边作等边三角形MDE,连接BE猜想的度数,并说明理由.
题型五:半角模型
21.如图,在等边 ABC中,在边上取两点、,使.若,,,则以、、为边长的三角形的形状为( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.随的值而定
22.如图,梯形ABCD中,AD∥BC,AB = BC = DC,点E、F分别在AD、AB上,且.(1)求证:;(2)连结AC,若,求的度数.
23.已知:正方形中,,绕点顺时针旋转,它的两边分别交(或它们的延长线)于点,,当绕点旋转到时(如图),易证.
(1)当绕点旋转到时(如图),上面的结论还成立吗?说明理由.
(2)当绕点旋转到如图的位置时,线段和之间又有怎样的数量关系?说明理由.
(3)图中,若,,求的面积为 .
24.如图1,已知 ABC是边长为5的等边三角形,以为底边作一个顶角为的等腰三角形.点M,N分别是边与边上的点,并且满足.
(1)尝试探究:要想证明为的平分线,小诚做了如下思考,如图2,延长至点F,使,连接,通过证明______,得到,进而证得______,得证为的平分线;(2)类比延伸:在(1)的思路下求的周长;
(3)拓展迁移:当点D在 ABC内部时,其他条件不变,直接写出的周长.
25.(1)如图①,在四边形中,,E,F分别是边上的点,且.请直接写出线段之间的数量关系: ;
(2)如图②,在四边形中,,E,F分别是边上的点,且.(1)中的结论是否仍然成立?请写出证明过程;
(3)在四边形中,,E,F分别是边所在直线上的点,且.请直接写出线段之间的数量关系: .
题型六:对角互补模型
26.如图,BN为∠MBC的平分线,P为BN上一点,且PD⊥BC于点D,∠APC+∠ABC=180°,给出下列结论:①∠MAP=∠BCP;②PA=PC;③AB+BC=2BD;④四边形BAPC的面积是△PBD面积的2倍,其中结论正确的个数有( )
A.4个 B.3个 C.2个 D.1个
27.小宇和小明一起进行数学游戏:已知,将等腰直角三角板摆放在平面内,使点A在的内部,且两个底角顶点B,C分别放在边上.
(1)如图1,小明摆放,恰好使得,又由于是等腰直角三角形,,从而直接可以判断出点A在的角平分线上.请回答:小明能够直接作出判断的数学依据是______.
(2)如图2,小宇调整了的位置,请判断平分是否仍然成立?若成立,请证明,若不成立,请举出反例.
28.如图,已知∠AOB=120°,在∠AOB的平分线OM上有一点C,将一个60°角的顶点与点C重合,它的两条边分别与直线OA、OB相交于点D、E.
(1)当∠DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OE+OD与OC的数量关系,并说明理由;(2)当∠DCE绕点C旋转到CD与OA不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;(3)当∠DCE绕点C旋转到CD与OA的反向延长线相交时,上述结论是否成立?若成立,请给于证明;若不成立,线段OD、OE与OC之间又有怎样的数量关系?请写出你的猜想,不需证明.
29.在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:BE+CF=AB.(3)如图3,若∠EDF的两边分别交AB、AC的延长线于E、F两点,(2)中的结论还成立吗?如果成立,请证明;如果不成立,请直接写出线段BE、AB、CF之间的数量关系.
30.已知:点是平分线上一点,点在射线上,作,交直线于点,作于点.
(1)观察猜想:如图,当时,写出和的数量关系,并说明理由.(2)探究证明:如图,当时,写出,和之间的等量关系,并说明理由.(3)拓展延伸:如图,当,点在射线的反向延长线上时,请直接写出线段、和之间的数量关系.
题型七:角平分线的全等模型(三类)
31.如图, ABC中,,,,平分,且,则与的面积和是 .
32.如图,在中,,和的平分线、相交于点,交于点,交于点,若已知周长为,,,则长为( )
A. B. C. D.4
33.利用角平分线构造全等三角形是常用的方法,如图,平分.点为上一点,过点作,垂足为,延长交于点,可证得,则,.
【问题提出】(1)如图,在中,平分,于点,若,,通过上述构造全等的办法,求的度数;
【问题探究】(2)如图,在中,,,平分,,垂足在的延长线上,试探究和的数量关系;
【问题解决】(3)如图是一块肥沃的土地,其中边与灌渠相邻,李伯伯想在这块地中划出一块直角三角形土地进行水稻试验,他进行了如下操作:
作的平分线;再过点作交于点
已知米,米,面积为平方米,求划出的的面积.
34.已知:如图,是的平分线,点是上的任意一点.,,垂足分别为点和点.求证:.
分析:图中有两个直角和,只要证明这两个三角形全等,便可证得.
(1)【问题解决】请根据教材分析,结合图①写出证明过程.
(2)【类比探究】如图②,是的平分线,是上任意一点,点M、N分别在、上,连接和,若,求证:.
35.(1)如图1,射线平分,在射线,上分别截取线段.;使;在射线上任取一点D,连接,.则与的数量关系为______.
(2)如图2,在中,,平分,求证:;
(3)如图3,在四边形中,,,,C为边中点,若平分,平分,,求的值.
参考答案
题型一:倍长中线
1.(1)解:如图,延长到,使,连接,点为的中点,,
在和中,,∴ BED≌ CAD(SAS),故答案为:A;
(2)解:∵ BED≌ CAD,,,
,,,
,,故答案为:;
解决问题:如图,延长交的延长线于点H,
四边形是正方形,,为边的中点,,
在和中,,∴ EAG≌ EBH(ASA),,,
∵AG=2,,,,
,,,,
,.
2.解∶(1)小王同学的思路:
如图1,以点为圆心,以长为半径画弧,交的延长线于点,则.所以.
因为,所以.
因为,所以.所以,即是的中点
小张同学的思路:如图2,以点为圆心,以长为半径画弧,交于点,连接,则.
所以,因为,所以.
因为,所以.
所以.所以,即是的中点;
(2)猜想方法1:如图3,以点为圆心,长为半径作弧,交的延长线于点,连接,
则.所以.因为,
所以,.
所以.所以.
又因为,所以.所以.
方法2:如图4,以点为圆心,以长为半径画弧,交于点,连接,
则.所以.
因为,所以.
因为,所以.
所以.所以.
因为,所以.所以.所以.
3.(1)解:在△ADC和△EDB中,,∴△ADC≌△EDB(SAS),故选:A;
(2)解:由(1)得:△ADC≌△EDB,∴AC=BE=6,
在△ABE中,AB BE(3)解:延长AD到M,使AD=DM,连接BM,如图②所示:
∵AD是△ABC中线,∴CD=BD,在△ADC和△MDB中,,
∴△ADC≌△MDB(SAS),∴BM=AC,∠CAD=∠M,
∵AC=BF,∴BM=BF,∴∠M=∠BFM,
∵∠AFE=∠BFM,∴∠BFM=∠CAD=∠M,∴AE=FE;
4.(1)证明:延长AD至M,使,连接MC.
在和∴ CDM中,,∴,∴,,
∵,∴,
∵,∴,∴,∴.
(2)线段DF与AD的数量关系为:.
证明如下:延长DF至点M,使,连接BM、AM,如图2所示:
∵点F为BE的中点,∴
在和中,∵,∴
∴,,∴
∵线段CD绕点D逆时针旋转120°得到线段DE
∴,,∴
∵是等边三角形∵,,
∴
∵,∴
在和中,∵,∴
∴,,∴
∴是等边三角形,∴.
5.(1)解:根据证明过程可得的依据是,故选:A;
(2)解:如图,延长至点,使.连接,
∵是边的中点∴.
∵,,∴.∴.
又,∴即∴.
(3)解:如图,延长,交于点,
∵,即,∴∵点是的中点,∴
又∴∴
∵平分∴∴,
∴∴
题型二:截长补短模型
6.(1)证明:方法一:∵平分,∴,
在和中,,,,
∴∴,,
∵,∴,∴,∴,∴;
方法二:延长到点E,使得,连接,
∴,则,
∵,∴,∵平分,∴,
在和中,,,,
∴,∴,∵,∴;
(2)在上取,连接,∵于,∴,∴,
∵,,∴,
∴,∴;
(3)如图所示,∵,为等边三角形,∴,,
∴∴,
∴,∴,∴,
过作,交于点,∴,
∵是的中点,∴,又,∴,
∴ ,,,而,
,∴,
又∵,∴,∴ , 即.
7.解:(1)方法1:在上截取,连接,
∵BD平分,,
在和中,,,,,
,,,,;
方法2:延长到,使,连接,
∵BD平分,,
在和中,,,,,
,,,,;
(2),,之间的数量关系为.
方法1:理由如下:如图,在上截取,连接,
由(1)知,,
,,,
为等边三角形, ,,
,为等边三角形,,,
,,,.
方法:理由:延长到,使,连接,
由(1)知,,是等边三角形, ,,
,,,
,为等边三角形,,,
,,即,
在和中,,,,
,;
(3)线段、、之间的数量关系为.连接,过点作于点,
,,,
在和中,,,,,
在和中,,,,
,.
8.(1)①∵是的角平分线,∴,
∵,,∴,∴;故答案为:;
②在上取点D,使,连接,,
∵△ABC的角平分线、相交于点P.∴平分,∴,
∵,∴,∴,,
∵,∴,∴,
∴,∴,∴,
∴,∴,
∵,∴,∴,∴;故答案为:;
(2),理由:在上取点E,使,连接,则,
∵,∴,
∵的平分线与的平分线恰好交于边上的点P,∴,,
∵,∴,∴,
∵,∴,∴,∴;
9.解:(1)在和中,∵,,,
∴,∴;
(2)解:选择②为条件,①为结论:如图,在取点N,使,连接,
∵平分,∴,
在和中,∵,,,
∴,∴,,
∵,,∴,∴,
∴,∴;
选择①为条件,②为结论:如图,在取点N,使,连接,
∵平分,∴,在和中,
∵,,,∴,∴,,
∵,∴,∴,
∴,∴,∵,∴;
10.(1)证明:在上截取,使得,连接,平分,∴,
,∴,,,
∵,,是的一个外角,,
,,,,;
(2)解:在上截取,连接,
,,∴,
,,,
,,,,
,,,,
,,,,
,,,的长为14.
题型三:一线三等角(K字型)模型
11.C
【详解】解:①,,
,,,故①正确;
②为中点,,,,,
,,,故②正确;
③,,,为等腰三角形,,,
,;或为等腰三角形,
,,,,故③错误;
④,,,
,,,
,,∴△ABD≌△DCE(ASA),,故④正确,
综上所述正确的有①②④.故选:.
12.3
【详解】解: ∵,∴,
∵,,∴,∴,∴,
在和中:,∴,
∴,∴,故答案为:3.
13.证明:(1)∵直线m,直线m,∴,
∵,∴,∵,∴,
∵在和中,∴,
∴,∴;
(2)结论仍然成立,理由是:∵,
∴,∴,
∵在和中,∴,
∴,∴.
(3)∵,∴,
在和中,,∴,∴,
设△ABC的底边上的高为h,则的底边上的高为h,
∴,,∵,∴,
∵,∴与的面积之和为.
14.(1)证明:①于,于,,
,,,
,;
②,,,;
(2)证明:,
,,,
在和中,,
,,;
(3)解:,理由如下:同(2)可证,
,,.
15.证明:(1)∵,,,∴,
∴,,∴,
在和△CFA中,,∴;
(2)∵,,,,
∴,,
在和△CAF中,,∴△ABE≌△CAF(ASA);
∴,,∴;
(3)∵△ABC的面积为17,,∴的面积是:,
根据解析(2)同理可证,∴,∴.
题型四:手拉手模型
16.D
【详解】解:∵和都是等腰直角三角形,∴,
又∵,∴,
即,∴,∴,①正确;
∵,∴,又∵,
∴,∴,即,③正确;
过点A分别作,垂足为点P,Q.
∵,∴,∴,∴,
∴点A在的平分线上,即平分,④正确.故选:D.
17.(1)证明:∵等边与等边的顶点,,三点在一条直线上,
∴∠ACB=∠DCP=60°,∠BCP=180°,∴∠ACD=180°-∠DCP -∠ACB=60°,
∴,∠ACP=∠DCP+∠ACD=120°,∴,
∵等边,等边,∴,,
在与中,∵,∴,∴.
(2)证明:如图1,过点作交于点,过点作交于点,
∵(1)中已证,又∵,,∴,
∵,,∴平分.
(3),理由如下:如图2,过点作交于点,过点作交于点,在上截取一点,使得,在上截取一点,使得,连接,,
∵,∴,∵,
又∵等边,∴,∴,
∵,∴,即,
∵,∴是等边三角形,∴,,
∵是等边三角形,∴,,∴,
即,在与△CAE中,∵,
∴,∴.∵,,∴,
同法可证,,∵,∴.
∵,,∴,
∵(2)中已证,∴,∴,即.
18.(1)解:①与位置关系是,数量关系是.
理由:,,.
又,,,且.
,,即.故答案为:,;
②都成立,,
在与中,,
,,,即.
(2)解:当时,.
理由:过点A作交的延长线于点G,则,
∵,∴,∴∴,
在与中,,∴,
∴,∴,即.
19.(1)∵∠ABC=∠DBE=60° ∴,
, ∴ ∵BA=BC,BD=BE
和中 ∴∴
和中∴∴∴为等边三角形;
(2)∵∠ABC=∠DBE=60°, BA=BC∴为等边三角形;∴
根据题意,AE和CD相交于点O ∵
∴
∵∴
∴,即直线AE和CD的夹角是故答案为:;
(3)∵∠ABC=∠DBE=60°, BA=BC∴为等边三角形;∴
∵,,∠ABC=∠DBE=60°∴
∵BA=BC,BD=BE 和中 ∴∴
如图,延长,交CD于点O
∴
∵∴
∴,即直线AE和CD的夹角是故答案为:;
(4)∵BA=BC,∴ ∵∠ACB=60°∴∴为等边三角形
∵BD=BE,∠ABC=∠DBE∴
∵, ∴
和中 ∴∴
分别延长CD、AE,相较于点O,如下图:
∴
∵∴
∴,即直线AE和CD的夹角是故答案为:.
20.(1)证明:问题初探:BE=CD.如图(1),∵∠DAE=∠BAC=90°,
∴∠BAE+∠BAD=∠BAD+∠CAD,∴∠BAE=∠CAD,
在△BAE和△CAD中,,∴△BAE≌△CAD(SAS),∴BE=CD;
(2)解:在图(2)中过点M作MF∥AC交BC于点F,
∵,,∴∠ACB=∠ABC=,
∵MF∥AC,∴∠BMF=∠A=90°,∠BFM=∠C=45°,∴MB=MF,
∵∠DME=∠BMF=90°,∴∠BME=∠DMF,
在△BME和△FMD中,,∴△BME≌△FMD(SAS),
∴∠MBE=∠MFD=45°;∴∠EBD=∠MBE+∠ABC=90°.故答案为:90°;
(3)解:BC=BD+BE.如图(3),∵△ABC和△ADE是等边三角形,
∴∠DAE=∠BAC=60°,∴∠BAE+∠BAD=∠BAD+∠CAD=60°,∴∠BAE=∠CAD,
在△BAE和△CAD中,,∴△BAE≌△CAD(SAS),∴BE=CD,∴BC=BD+CD=BD+BE;
(4)拓展创新:∠EBD=120°.理由:在图(4)中过点M作MG∥AC交BC于点G,
如图则∠BMG=∠A=60°,∠BGM=∠C=60°,∴△BMG是等边三角形,∴BM=GM,
∵∠DME=∠BMG=60°,∴∠BME+∠BMD=∠BMD+∠GMD=60°,∴∠BME=∠DMG,
在△BME和△GMD中,,∴△BME≌△GMD(SAS),
∴∠MBE=∠MGB=60°,∴∠EBD=∠MBE+∠MBG=120°.
题型五:半角模型
21.C
【详解】解:如图所示:将绕点顺时针旋转得到,连接,
由旋转性质可知,,,,,
∵△ABC是等边三角形,∴,∵,∴,
∴,∴,
在与中,,∴,∴,
∵,,∴,
∴以、、为边长的三角形的形状为钝角三角形,故选:C.
22.(1)旋转△BCF使BC与CD重合,
∵AD∥BC,AB=DC,即梯形ABCD为等腰梯形,
∴∠A=∠ADC,∠A+∠ABC=180°,∴∠ADC+∠ABC=180°,
由旋转可知:∠ABC=∠CDF′,∴∠ADC+∠CDF′=180°,即∠ADF′为平角,∴A,D,F′共线,
∵∴∠BCF+∠ECD=∠ECF=∠BCD,
∵FC=F′C,EC=EC,∠ECF'=∠BCF+∠DCE=∠ECF,∴△FCE≌△F′CE,∴EF′=EF=DF′+ED,∴BF=EF -ED;
(2)∵AB=BC,∠B=80°,∴∠ACB=50°,由(1)得∠FEC=∠DEC=70°,
又∵AD//BC,∴∠ECB=70°,而∠B=∠BCD=80°,
∴∠DCE=10°,∴∠BCF=30°,∴∠ACF=∠BCA -∠BCF=20°.
23.(1)解:上面的结论还成立,理由如下:
如图,在的延长线上,截取,连接,
在和中, ,∴,∴,,
∵,,∴,∴,∴,
在和中,,∴,∴,
∵,∴;
(2)解:,理由如下:如图,在上截取,连接
在和中,,∴,
∴,,∴ ,即,
∵,∴
在和中,,∴,
∴,∴,∴;
(3)解:∵ ,∴,
∴的面积,∴的面积为,故答案为:.
24.(1)延长至点F,使,连接,
由题意得,,,∴,
∴,∴,
∵,∴,∴,.
∵,,∴,∴,
∵,∴,∴,∴平分.
(2)∵,∴.∵,∴.
∴的周长为:.
(3)延长交于P,延长交于Q,令,连接,
∵是等腰三角形,且,∴,,,
∵△ABC是等边三角形,∴,
∴,,,∴,,
在和中, ,∴ ,∴,,
∵ ,,∴,
在和中, ∴ ,∴,,
∵ ,,∴,∴即,
在和中, ,∴ ,∴.
∴的周长为:.
25.解:(1)如图1,延长到G,使,连接,
∵∴
∴,∴∴.
∵,∴△AEF≌△AEG.∴.
∵.∴;故答案为:;
(2)(1)中的结论仍然成立.
理由是:如图2,延长到G,使,连接
∵,∴
∵∴∴,
∴∴.
∵,∴△AEF≌△AEG.∴.∵.∴;
(3)若如图1,则结论成立,若如图3,则或
证明:在上截取,使,连接.
∵,∴.
∵∴∴
∴.∴
∵,∴△AEF≌△AEG∴.∵∴.同理可得:
∵∴.故答案为:或或.
题型六:对角互补模型
26.A
【详解】解:过点P作PK⊥AB,垂足为点K.∵PK⊥AB,PD⊥BC,∠ABP=∠CBP,∴PK=PD,
在Rt△BPK和Rt△BPD中,,∴Rt△BPK≌Rt△BPD(HL),∴BK=BD,
∵∠APC+∠ABC=180°,且∠ABC+∠KPD=180°,∴∠KPD=∠APC,∴∠APK=∠CPD,故①正确,
在△PAK和△PCD中,,∴△PAK≌△PCD(ASA),∴AK=CD,PA=PC,故②正确,
∴BK﹣AB=BC﹣BD,∴BD﹣AB=BC﹣BD,∴AB+BC=2BD,故③正确,
∵Rt△BPK≌Rt△BPD,△PAK≌△PCD(ASA),∴S△BPK=S△BPD,S△APK=S△PDC,
∴S四边形ABCP=S四边形KBDP=2S△PBD.故④正确.故选A.
27.(1)解:因为,,根据角的内部到角的两边距离相等的点,都在这个角的平分线上,所以点A在的角平分线上
故答案为:角的内部到角的两边距离相等的点,都在这个角的平分线上.
(2)结论:平分仍然成立;
证明:如解图3,过点A作,,∴,
又∵,∴,∴,
又∵,∴,
在和中,∴∴,
又∵,,∴平分,故(1)结论正确.
28.(1)∵OM是∠AOB的角平分线,∴∠AOC=∠BOC=∠AOB=60°,
∵CD⊥OA,∴∠ODC=90°,∴∠OCD=30°,∴∠OCE=∠DCE﹣∠OCD=30°,
在Rt△OCD中,OD=OC,同理:OE=OC,∴OD+OE=OC,
(2)(1)中结论仍然成立,理由:过点C作CF⊥OA于F,CG⊥OB于G,如图,
∴∠OFC=∠OGC=90°,∵∠AOB=120°,∴∠FCG=60°,
同(1)的方法得,OF=OC,OG=OC,∴OF+OG=OC,
∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,∴CF=CG,
∵∠DCE=60°,∠FCG=60°,∴∠DCF=∠ECG,∴△CFD≌△CGE,∴DF=EG,
∴OF=OD+DF=OD+EG,OG=OE﹣EG, ∴OF+OG=OD+EG+OE﹣EG=OD+OE,∴OD+OE=OC;
(3)(1)中结论不成立,结论为:OE﹣OD=OC,理由:过点C作CF⊥OA于F,CG⊥OB于G,如图,
∴∠OFC=∠OGC=90°,∵∠AOB=120°,∴∠FCG=60°,同(1)的方法得,OF=OC,OG=OC,∴OF+OG=OC,
∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,∴CF=CG,
∵∠DCE=60°,∠FCG=60°,∴∠DCF=∠ECG,∴△CFD≌△CGE,
∴DF=EG,∴OF=DF﹣OD=EG﹣OD,OG=OE﹣EG,
∴OF+OG=EG﹣OD+OE﹣EG=OE﹣OD,∴OE﹣OD=OC.
29.解:(1)如图1中,
∵AB=AC,∠A=60°,∴△ABC是等边三角形,∴∠B=∠C=60°,BC=AC=AB=4,
∵点D是线段BC的中点,∴BD=DC=BC=2,∵DF⊥AC,即∠CFD=90°,∴∠CDF=30°,
又∵∠EDF=120°,∴∠EDB=30°,∴∠BED=90°∴BE=BD=1.
(2)如图2中,过点D作DM⊥AB于M,作DN⊥AC于N.
∵∠B=∠C=60°,BD=DC,∠BDM=∠CDN=30°,∴△BDM≌△CDN,∴BM=CN,DM=DN,
又∵∠EDF=120°=∠MDN,∴∠EDM=∠NDF,
又∵∠EMD=∠FND=90°,∴△EDM≌△FDN,∴ME=NF,∴BE+CF=BM+EM+NC﹣FN=2BM=BD=AB.
(3)结论不成立.结论:BE﹣CF=AB.
∵∠B=∠C=60°,BD=DC,∠BDM=∠CDN=30°,∴△BDM≌△CDN,∴BM=CN,DM=DN,
又∵∠EDF=120°=∠MDN,∴∠EDM=∠NDF,
又∵∠EMD=∠FND=90°,∴△EDM≌△FDN,∴ME=NF,∴BE﹣CF=BM+EM﹣(FN﹣CN)=2BM=BD=AB.
30.(1)解:.理由:过点作于点,
∵点在的角平分线上,且于,,∴,,
∵,∴,,∴,
在和中,,∴(),∴.
(2)解:结论:,理由如下:如图,过点作于点,
同(),可证,,∴,
∵,∴,∴,∴,∴.
(3)解:,理由如下:如图,过点作于点,
同(),可证,,∴,
∵,∴,∴,∴,∴.
题型七:角平分线的全等模型(三类)
31.3
【详解】解:如下图,延长交于点,
∵,,,∴,
∵平分,∴,∵,∴,
在和中,,∴,
∴,,∴,∴.故答案为:3.
32.B
【详解】解:如图,在上截取,连接
平分,平分,,
,,,
,,
在和中,,,
,,,
在和中,,,
,,
周长为,,,
,.故选:B.
33.()如图, 延长交于点,由已知可知,∴,
∵,∴;
(),证明如下:如图,延长交于点,则,
∵,∴,∵,∴,
又∵,∴,∴,由已知可知,,∴;
()如图,延长交于,由已知可知,,,∴,
∵,∴,∴.
34.(1)证明:,,,
是的平分线,,
在和中,,,;
(2)证明:如图②,过点作于,于,
是的平分线,,,,
,,,
在和中,,,.
35.(1)证明:射线平分,,
又,,,,故答案为:;
(2)证明:在上截取,连接,如图2所示:
平分,,又,,
,,,,,,
又,,,,,
,;
(3)解:在上取点,使,连接,在上取点,使,连接,如图3所示:
是边的中点,,,
平分,,又,,
,,.同理可证:,
,,,,,
,,,
,是等边三角形,,.
题型一:倍长中线
1.综合与实践:小明遇到这样一个问题,如图1,中,,,点为的中点,求的取值范围.
小明发现老师讲过的“倍长中线法”可以解决这个问题,所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法,他的做法是:如图2,延长到,使,连接,构造,经过推理和计算使问题得到解决
请回答:(1)小明证明用到的判定定理是:________;(填入你选择的选项字母)
A. B. C. D.
(2)的取值范围是________.
小明还发现:倍长中线法最重要的一点就是延长中线一倍,完成全等三角形模型的构造.
参考小明思考问题的方法,解决问题:
如图3,在正方形中,为边的中点,、分别为,边上的点,若,,,求的长.
2.【问题提出】期末复习课上,数学丁老师出示了下面一个问题:如图1,在中,是延长线的点,是边上一点,且满足,那么是的中点,请你说明理由.
【思路探究】小王同学从条件出发分析解题思路:以为腰构造等腰和平行八字型全等三角形,如图2,以点为圆心,以长为半径画弧,交的延长线于点,先应用等腰三角形的轴对称性,再应用三角形全等“”(或“”)的判定方法即可得,小张同学从结论出发分析解题思路:以为腰构造等腰,将说明的问题转化为说明的问题,如图3,以点为圆心,以长为半径画弧,交于点,于是可得,再应用三角形全等“”(或“”)的判定方法即可得.
(1)请你选择小张同学或小王同学的思路或按自己的思路写出完整的解题过程;
【学以致用】(2)请你在理解了小张同学或小王同学解题思路的基础上,解答下面一道图形较为复杂的同类问题:如图4,在四边形中,,过点作线段,且,连接,交的延长于点,猜想与的数量关系并说明理由.
3.【问题情境】课外兴趣小组活动时,老师提出了如下问题:
如图①,△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB,依据是 .A.SAS;B. SSS;C. AAS;D. HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
(3)【初步运用】如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AC=BF.求证AE=FE.
4.阅读材料:如图1,在中,D,E分别是边AB,AC的中点,小亮在证明“三角形的中位线平行于第三边,且等于第三边的一半”时,通过延长DE到点F,使,连接CF,证明,再证四边形DBCF是平行四边形即得证.
类比迁移:(1)如图2,AD是的中线,E是AC上的一点,BE交AD于点F,且,求证:.
小亮发现可以类比材料中的思路进行证明.
证明:如图2,延长AD至点M,使,连接MC,……
请根据小亮的思路完成证明过程.
方法运用:(2)如图3,在等边中,D是射线BC上一动点(点D在点C的右侧),连接AD.把线段CD绕点D逆时针旋转120°得到线段DE,F是线段BE的中点,连接DF、CF.请你判断线段DF与AD的数量关系,并给出证明.
5.阅读与思考:下面是小宇同学的数学日记,请仔细阅读,并完成相应的任务.
“倍长中线法”中线是三角形中的重要线段之一,利用中线解决几何问题时,常常采用“倍长中线法”加辅助线. 如图1.在中,平分,且恰好是边的中点.求证:. 证明:如图2,延长至点,使.∵是边的中点 ∴. ∵,,∴(依据).∴. ∵平分,∴,∴,∴,∴.
任务:(1)材料中的“依据”是________.(填选项)
A. B. C. D.
(2)在中,,,则边上的中线长度的取值范围是________.(3)如图3,在四边形中,,平分,且是的中点,,,求的长.
题型二:截长补短模型
6.【方法探究】如图1,在中,平分,,探究,,之间的数量关系;
嘉铭同学通过思考发现,可以通过“截长、补短”两种方法解决问题:
方法1:如图2,在上截取,使得,连接,可以得到全等三角形,进而解决此问题.
方法2:如图3,延长到点,使得 ,连接,可以得到等腰三角形,进而解决此问题.
(1)根据探究,直接写出,,之间的数量关系;
【迁移应用】(2)如图4,在中,D是上一点,,,于,探究,,之间的数量关系,并证明.
【拓展延伸】(3)如图5,为等边三角形,点为延长线上一动点,连接.以为边在上方作等边,点是的中点,连接并延长,交的延长线于点.若,求证:.
7.(1)阅读理解:问题:如图1,在四边形中,对角线平分,.求证:.
思考:“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题.
方法1:在上截取,连接,得到全等三角形,进而解决问题;
方法2:延长到点,使得,连接,得到全等三角形,进而解决问题.
结合图1,在方法1和方法2中任选一种,添加辅助线并完成证明.
(2)问题解决:如图2,在(1)的条件下,连接,当时,探究线段,,之间的数量关系,并说明理由;
(3)问题拓展:如图3,在四边形中,,,过点作,垂足为点,请写出线段、、之间的数量关系.
8.李老师善于通过合适的主题整合教学内容,帮助同学们用整体的、联系的、发展的眼光看问题,形成科学的思维习惯,下面是李老师在“利用角的对称性构造全等模型”主题下设计的问题,请你解答.
(1)【观察发现】①如图1,是 ABC的角平分线,,在上截取,连接,则与的数量关系是__________;
②如图2, ABC的角平分线、相交于点P.当时,线段与的数量关系是__________;
(2)【探究迁移】如图3,在四边形中,,的平分线与的平分线恰好交于边上的点P,试判断与的数量关系,并说明理由.
9.【实际情境】手工课堂上,老师给每个制作小组发放一把花折伞和制作花折伞的材料及工具.同学们认真观察后,组装了花折伞的骨架,粘贴了彩色伞面,制作出精美的花折伞.
【模型建立】(1)如图1,从花折伞中抽象出“伞形图”.,.求证:.
【模型应用】(2)如图2,中,的平分线交于点.请你从以下两个条件:①;②中选择一个作为已知条件,另一个作为结论,并写出结论成立的证明过程.(注:只需选择一种情况作答)
10.阅读材料:截长补短法,是初中数学几何题中一种辅助线的添加方法.截长就是在长边上截取一条线段与某一短边相等,补短是通过在一条短边上延长一条线段与另一长边相等,从而解决问题.依据上述材料,解答下列问题:如图1,在 ABC中,平分,交于点,且,求证:.
(1)为了证明结论“”,小亮在上截取,使得,连接,解答了这个问题,请按照小亮的思路写证明过程;(提示:如果一个三角形有两个角相等,那么这两个角所对的边也相等)
(2)如图2,在四边形中,已知,,,,是的高,,,求的长.
题型三:一线三等角(K字型)模型
11.如图,中,,,为线段上一动点(不与点,重合),连接,作 ,交线段于,以下四个结论:
①;②当为中点时,;③当 ADE为等腰三角形时,;
④当时,.其中正确的结论的个数是( )
A. B. C. D.
12.如图,在中,,,点D为上一点,连接.过点B作于点E,过点C作交的延长线于点F.若,,则的长度为 .
13.(1)已知:如图①,在 ABC中,,,直线m经过点A,直线m,直线m,垂足分别为D,E.求证:.
(2)拓展:如图②,将(1)中的条件改为:在 ABC中,,D,A,E三点都在直线m上,并且有,其中为任意锐角或钝角:那么结论是否仍成立?若成立,请你给出证明;若不成立,请说明理由.
(3)应用,如图③,在 ABC中,是钝角,,,,直线m与的延长线交于点F,若, ABC的面积是15,求与的面积之和.
14.在 ABC中,,,直线经过点,且于,于.
(1)当直线绕点旋转到图1的位置时,求证:①;②;
(2)当直线绕点旋转到图2的位置时,求证:;
(3)当直线绕点旋转到图3的位置时,试问、、具有怎样的等量关系?请写出这个等量关系,并加以证明.
15.(1)如图①,,射线在这个角的内部,点B、C分别在的边、上,且,于点F,于点D.求证: ABD≌ CAF;
(2)如图②,点B、C分别在的边、上,点E、F都在内部的射线上,、分别是、 CAF的外角.已知,且.求证:;
(3)如图③,在 ABC中,,.点D在边上,,点E、F在线段上,.若 ABC的面积为17,求与 BDE的面积之和.
题型四:手拉手模型
16.已知:如图,分别以的边为腰向外作等腰直角、等腰直角,连接相交于点O,连接,①,②,③,④平分,⑤平分,则以上结论正确的有( )
A.①③⑤ B.②③④ C.③④⑤ D.①③④
17.如图1,等边与等边的顶点,,三点在一条直线上,连接交于点,连.(1)求证:;(2)求证:平分;
(3)设,若,直接写出a,b,c之间满足的数量关系.
18.如图,在 ABC中,为锐角,点D为直线上一动点,以为直角边且在的右侧作等腰直角三角形,,.
(1)如果,.①当点D在线段上时,如图1,线段、的位置关系为________,数量关系为________;②当点D在线段的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.(2)如图3,如果,,点D在线段上运动.探究:当多少度时,?请说明理由.
19.已知:△ABC与△BDE都是等腰三角形.BA=BC,BD=BE(AB>BD)且有∠ABC=∠DBE.(1)如图1,如果A、B、D在一直线上,且∠ABC=60°,求证:△BMN是等边三角形;(2)在第(1)问的情况下,直线AE和CD的夹角是 °;
(3)如图2,若A、B、D不在一直线上,但∠ABC=60°的条件不变则直线AE和CD的夹角是 °;
(4)如图3,若∠ACB=60°,直线AE和CD的夹角是 °.
20.【知识背景】我们在第十一章《三角形》中学习了三角形的边与角的性质,在第十二章《全等三角形》中学习了全等三角形的性质和判定,在第十三章《轴对称》中学习了等腰三角形的性质和判定.在一些探究题中经常用以上知识转化角和边,进而解决问题.
(1)【问题初探】如图(1),中,,,点D是BC上一点,连接AD,以AD为一边作 ADE,使,,连接BE,猜想BE和CD有怎样的数量关系,并说明理由.
(2)【类比再探】如图(2),中,,,点M是AB上一点,点D是BC上一点,连接MD,以MD为一边作,使,,连接BE,则______.(直接写出答案,不写过程;需要作辅助线的,请说明辅助线的作法,并在图(2)中作出辅助线)
(3)【方法迁移】如图(3),是等边三角形,点D是BC上一点,连接AD,以AD为一边作等边三角形ADE连接BE,则BD,BE,BC之间有怎样的数量关系?(直接写出答案,不写过程).
(4)【数学思考】如图(4),是等边三角形,点M是AB上一点,点D是BC上一点,连接MD,以MD为一边作等边三角形MDE,连接BE猜想的度数,并说明理由.
题型五:半角模型
21.如图,在等边 ABC中,在边上取两点、,使.若,,,则以、、为边长的三角形的形状为( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.随的值而定
22.如图,梯形ABCD中,AD∥BC,AB = BC = DC,点E、F分别在AD、AB上,且.(1)求证:;(2)连结AC,若,求的度数.
23.已知:正方形中,,绕点顺时针旋转,它的两边分别交(或它们的延长线)于点,,当绕点旋转到时(如图),易证.
(1)当绕点旋转到时(如图),上面的结论还成立吗?说明理由.
(2)当绕点旋转到如图的位置时,线段和之间又有怎样的数量关系?说明理由.
(3)图中,若,,求的面积为 .
24.如图1,已知 ABC是边长为5的等边三角形,以为底边作一个顶角为的等腰三角形.点M,N分别是边与边上的点,并且满足.
(1)尝试探究:要想证明为的平分线,小诚做了如下思考,如图2,延长至点F,使,连接,通过证明______,得到,进而证得______,得证为的平分线;(2)类比延伸:在(1)的思路下求的周长;
(3)拓展迁移:当点D在 ABC内部时,其他条件不变,直接写出的周长.
25.(1)如图①,在四边形中,,E,F分别是边上的点,且.请直接写出线段之间的数量关系: ;
(2)如图②,在四边形中,,E,F分别是边上的点,且.(1)中的结论是否仍然成立?请写出证明过程;
(3)在四边形中,,E,F分别是边所在直线上的点,且.请直接写出线段之间的数量关系: .
题型六:对角互补模型
26.如图,BN为∠MBC的平分线,P为BN上一点,且PD⊥BC于点D,∠APC+∠ABC=180°,给出下列结论:①∠MAP=∠BCP;②PA=PC;③AB+BC=2BD;④四边形BAPC的面积是△PBD面积的2倍,其中结论正确的个数有( )
A.4个 B.3个 C.2个 D.1个
27.小宇和小明一起进行数学游戏:已知,将等腰直角三角板摆放在平面内,使点A在的内部,且两个底角顶点B,C分别放在边上.
(1)如图1,小明摆放,恰好使得,又由于是等腰直角三角形,,从而直接可以判断出点A在的角平分线上.请回答:小明能够直接作出判断的数学依据是______.
(2)如图2,小宇调整了的位置,请判断平分是否仍然成立?若成立,请证明,若不成立,请举出反例.
28.如图,已知∠AOB=120°,在∠AOB的平分线OM上有一点C,将一个60°角的顶点与点C重合,它的两条边分别与直线OA、OB相交于点D、E.
(1)当∠DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OE+OD与OC的数量关系,并说明理由;(2)当∠DCE绕点C旋转到CD与OA不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;(3)当∠DCE绕点C旋转到CD与OA的反向延长线相交时,上述结论是否成立?若成立,请给于证明;若不成立,线段OD、OE与OC之间又有怎样的数量关系?请写出你的猜想,不需证明.
29.在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:BE+CF=AB.(3)如图3,若∠EDF的两边分别交AB、AC的延长线于E、F两点,(2)中的结论还成立吗?如果成立,请证明;如果不成立,请直接写出线段BE、AB、CF之间的数量关系.
30.已知:点是平分线上一点,点在射线上,作,交直线于点,作于点.
(1)观察猜想:如图,当时,写出和的数量关系,并说明理由.(2)探究证明:如图,当时,写出,和之间的等量关系,并说明理由.(3)拓展延伸:如图,当,点在射线的反向延长线上时,请直接写出线段、和之间的数量关系.
题型七:角平分线的全等模型(三类)
31.如图, ABC中,,,,平分,且,则与的面积和是 .
32.如图,在中,,和的平分线、相交于点,交于点,交于点,若已知周长为,,,则长为( )
A. B. C. D.4
33.利用角平分线构造全等三角形是常用的方法,如图,平分.点为上一点,过点作,垂足为,延长交于点,可证得,则,.
【问题提出】(1)如图,在中,平分,于点,若,,通过上述构造全等的办法,求的度数;
【问题探究】(2)如图,在中,,,平分,,垂足在的延长线上,试探究和的数量关系;
【问题解决】(3)如图是一块肥沃的土地,其中边与灌渠相邻,李伯伯想在这块地中划出一块直角三角形土地进行水稻试验,他进行了如下操作:
作的平分线;再过点作交于点
已知米,米,面积为平方米,求划出的的面积.
34.已知:如图,是的平分线,点是上的任意一点.,,垂足分别为点和点.求证:.
分析:图中有两个直角和,只要证明这两个三角形全等,便可证得.
(1)【问题解决】请根据教材分析,结合图①写出证明过程.
(2)【类比探究】如图②,是的平分线,是上任意一点,点M、N分别在、上,连接和,若,求证:.
35.(1)如图1,射线平分,在射线,上分别截取线段.;使;在射线上任取一点D,连接,.则与的数量关系为______.
(2)如图2,在中,,平分,求证:;
(3)如图3,在四边形中,,,,C为边中点,若平分,平分,,求的值.
参考答案
题型一:倍长中线
1.(1)解:如图,延长到,使,连接,点为的中点,,
在和中,,∴ BED≌ CAD(SAS),故答案为:A;
(2)解:∵ BED≌ CAD,,,
,,,
,,故答案为:;
解决问题:如图,延长交的延长线于点H,
四边形是正方形,,为边的中点,,
在和中,,∴ EAG≌ EBH(ASA),,,
∵AG=2,,,,
,,,,
,.
2.解∶(1)小王同学的思路:
如图1,以点为圆心,以长为半径画弧,交的延长线于点,则.所以.
因为,所以.
因为,所以.所以,即是的中点
小张同学的思路:如图2,以点为圆心,以长为半径画弧,交于点,连接,则.
所以,因为,所以.
因为,所以.
所以.所以,即是的中点;
(2)猜想方法1:如图3,以点为圆心,长为半径作弧,交的延长线于点,连接,
则.所以.因为,
所以,.
所以.所以.
又因为,所以.所以.
方法2:如图4,以点为圆心,以长为半径画弧,交于点,连接,
则.所以.
因为,所以.
因为,所以.
所以.所以.
因为,所以.所以.所以.
3.(1)解:在△ADC和△EDB中,,∴△ADC≌△EDB(SAS),故选:A;
(2)解:由(1)得:△ADC≌△EDB,∴AC=BE=6,
在△ABE中,AB BE
∵AD是△ABC中线,∴CD=BD,在△ADC和△MDB中,,
∴△ADC≌△MDB(SAS),∴BM=AC,∠CAD=∠M,
∵AC=BF,∴BM=BF,∴∠M=∠BFM,
∵∠AFE=∠BFM,∴∠BFM=∠CAD=∠M,∴AE=FE;
4.(1)证明:延长AD至M,使,连接MC.
在和∴ CDM中,,∴,∴,,
∵,∴,
∵,∴,∴,∴.
(2)线段DF与AD的数量关系为:.
证明如下:延长DF至点M,使,连接BM、AM,如图2所示:
∵点F为BE的中点,∴
在和中,∵,∴
∴,,∴
∵线段CD绕点D逆时针旋转120°得到线段DE
∴,,∴
∵是等边三角形∵,,
∴
∵,∴
在和中,∵,∴
∴,,∴
∴是等边三角形,∴.
5.(1)解:根据证明过程可得的依据是,故选:A;
(2)解:如图,延长至点,使.连接,
∵是边的中点∴.
∵,,∴.∴.
又,∴即∴.
(3)解:如图,延长,交于点,
∵,即,∴∵点是的中点,∴
又∴∴
∵平分∴∴,
∴∴
题型二:截长补短模型
6.(1)证明:方法一:∵平分,∴,
在和中,,,,
∴∴,,
∵,∴,∴,∴,∴;
方法二:延长到点E,使得,连接,
∴,则,
∵,∴,∵平分,∴,
在和中,,,,
∴,∴,∵,∴;
(2)在上取,连接,∵于,∴,∴,
∵,,∴,
∴,∴;
(3)如图所示,∵,为等边三角形,∴,,
∴∴,
∴,∴,∴,
过作,交于点,∴,
∵是的中点,∴,又,∴,
∴ ,,,而,
,∴,
又∵,∴,∴ , 即.
7.解:(1)方法1:在上截取,连接,
∵BD平分,,
在和中,,,,,
,,,,;
方法2:延长到,使,连接,
∵BD平分,,
在和中,,,,,
,,,,;
(2),,之间的数量关系为.
方法1:理由如下:如图,在上截取,连接,
由(1)知,,
,,,
为等边三角形, ,,
,为等边三角形,,,
,,,.
方法:理由:延长到,使,连接,
由(1)知,,是等边三角形, ,,
,,,
,为等边三角形,,,
,,即,
在和中,,,,
,;
(3)线段、、之间的数量关系为.连接,过点作于点,
,,,
在和中,,,,,
在和中,,,,
,.
8.(1)①∵是的角平分线,∴,
∵,,∴,∴;故答案为:;
②在上取点D,使,连接,,
∵△ABC的角平分线、相交于点P.∴平分,∴,
∵,∴,∴,,
∵,∴,∴,
∴,∴,∴,
∴,∴,
∵,∴,∴,∴;故答案为:;
(2),理由:在上取点E,使,连接,则,
∵,∴,
∵的平分线与的平分线恰好交于边上的点P,∴,,
∵,∴,∴,
∵,∴,∴,∴;
9.解:(1)在和中,∵,,,
∴,∴;
(2)解:选择②为条件,①为结论:如图,在取点N,使,连接,
∵平分,∴,
在和中,∵,,,
∴,∴,,
∵,,∴,∴,
∴,∴;
选择①为条件,②为结论:如图,在取点N,使,连接,
∵平分,∴,在和中,
∵,,,∴,∴,,
∵,∴,∴,
∴,∴,∵,∴;
10.(1)证明:在上截取,使得,连接,平分,∴,
,∴,,,
∵,,是的一个外角,,
,,,,;
(2)解:在上截取,连接,
,,∴,
,,,
,,,,
,,,,
,,,,
,,,的长为14.
题型三:一线三等角(K字型)模型
11.C
【详解】解:①,,
,,,故①正确;
②为中点,,,,,
,,,故②正确;
③,,,为等腰三角形,,,
,;或为等腰三角形,
,,,,故③错误;
④,,,
,,,
,,∴△ABD≌△DCE(ASA),,故④正确,
综上所述正确的有①②④.故选:.
12.3
【详解】解: ∵,∴,
∵,,∴,∴,∴,
在和中:,∴,
∴,∴,故答案为:3.
13.证明:(1)∵直线m,直线m,∴,
∵,∴,∵,∴,
∵在和中,∴,
∴,∴;
(2)结论仍然成立,理由是:∵,
∴,∴,
∵在和中,∴,
∴,∴.
(3)∵,∴,
在和中,,∴,∴,
设△ABC的底边上的高为h,则的底边上的高为h,
∴,,∵,∴,
∵,∴与的面积之和为.
14.(1)证明:①于,于,,
,,,
,;
②,,,;
(2)证明:,
,,,
在和中,,
,,;
(3)解:,理由如下:同(2)可证,
,,.
15.证明:(1)∵,,,∴,
∴,,∴,
在和△CFA中,,∴;
(2)∵,,,,
∴,,
在和△CAF中,,∴△ABE≌△CAF(ASA);
∴,,∴;
(3)∵△ABC的面积为17,,∴的面积是:,
根据解析(2)同理可证,∴,∴.
题型四:手拉手模型
16.D
【详解】解:∵和都是等腰直角三角形,∴,
又∵,∴,
即,∴,∴,①正确;
∵,∴,又∵,
∴,∴,即,③正确;
过点A分别作,垂足为点P,Q.
∵,∴,∴,∴,
∴点A在的平分线上,即平分,④正确.故选:D.
17.(1)证明:∵等边与等边的顶点,,三点在一条直线上,
∴∠ACB=∠DCP=60°,∠BCP=180°,∴∠ACD=180°-∠DCP -∠ACB=60°,
∴,∠ACP=∠DCP+∠ACD=120°,∴,
∵等边,等边,∴,,
在与中,∵,∴,∴.
(2)证明:如图1,过点作交于点,过点作交于点,
∵(1)中已证,又∵,,∴,
∵,,∴平分.
(3),理由如下:如图2,过点作交于点,过点作交于点,在上截取一点,使得,在上截取一点,使得,连接,,
∵,∴,∵,
又∵等边,∴,∴,
∵,∴,即,
∵,∴是等边三角形,∴,,
∵是等边三角形,∴,,∴,
即,在与△CAE中,∵,
∴,∴.∵,,∴,
同法可证,,∵,∴.
∵,,∴,
∵(2)中已证,∴,∴,即.
18.(1)解:①与位置关系是,数量关系是.
理由:,,.
又,,,且.
,,即.故答案为:,;
②都成立,,
在与中,,
,,,即.
(2)解:当时,.
理由:过点A作交的延长线于点G,则,
∵,∴,∴∴,
在与中,,∴,
∴,∴,即.
19.(1)∵∠ABC=∠DBE=60° ∴,
, ∴ ∵BA=BC,BD=BE
和中 ∴∴
和中∴∴∴为等边三角形;
(2)∵∠ABC=∠DBE=60°, BA=BC∴为等边三角形;∴
根据题意,AE和CD相交于点O ∵
∴
∵∴
∴,即直线AE和CD的夹角是故答案为:;
(3)∵∠ABC=∠DBE=60°, BA=BC∴为等边三角形;∴
∵,,∠ABC=∠DBE=60°∴
∵BA=BC,BD=BE 和中 ∴∴
如图,延长,交CD于点O
∴
∵∴
∴,即直线AE和CD的夹角是故答案为:;
(4)∵BA=BC,∴ ∵∠ACB=60°∴∴为等边三角形
∵BD=BE,∠ABC=∠DBE∴
∵, ∴
和中 ∴∴
分别延长CD、AE,相较于点O,如下图:
∴
∵∴
∴,即直线AE和CD的夹角是故答案为:.
20.(1)证明:问题初探:BE=CD.如图(1),∵∠DAE=∠BAC=90°,
∴∠BAE+∠BAD=∠BAD+∠CAD,∴∠BAE=∠CAD,
在△BAE和△CAD中,,∴△BAE≌△CAD(SAS),∴BE=CD;
(2)解:在图(2)中过点M作MF∥AC交BC于点F,
∵,,∴∠ACB=∠ABC=,
∵MF∥AC,∴∠BMF=∠A=90°,∠BFM=∠C=45°,∴MB=MF,
∵∠DME=∠BMF=90°,∴∠BME=∠DMF,
在△BME和△FMD中,,∴△BME≌△FMD(SAS),
∴∠MBE=∠MFD=45°;∴∠EBD=∠MBE+∠ABC=90°.故答案为:90°;
(3)解:BC=BD+BE.如图(3),∵△ABC和△ADE是等边三角形,
∴∠DAE=∠BAC=60°,∴∠BAE+∠BAD=∠BAD+∠CAD=60°,∴∠BAE=∠CAD,
在△BAE和△CAD中,,∴△BAE≌△CAD(SAS),∴BE=CD,∴BC=BD+CD=BD+BE;
(4)拓展创新:∠EBD=120°.理由:在图(4)中过点M作MG∥AC交BC于点G,
如图则∠BMG=∠A=60°,∠BGM=∠C=60°,∴△BMG是等边三角形,∴BM=GM,
∵∠DME=∠BMG=60°,∴∠BME+∠BMD=∠BMD+∠GMD=60°,∴∠BME=∠DMG,
在△BME和△GMD中,,∴△BME≌△GMD(SAS),
∴∠MBE=∠MGB=60°,∴∠EBD=∠MBE+∠MBG=120°.
题型五:半角模型
21.C
【详解】解:如图所示:将绕点顺时针旋转得到,连接,
由旋转性质可知,,,,,
∵△ABC是等边三角形,∴,∵,∴,
∴,∴,
在与中,,∴,∴,
∵,,∴,
∴以、、为边长的三角形的形状为钝角三角形,故选:C.
22.(1)旋转△BCF使BC与CD重合,
∵AD∥BC,AB=DC,即梯形ABCD为等腰梯形,
∴∠A=∠ADC,∠A+∠ABC=180°,∴∠ADC+∠ABC=180°,
由旋转可知:∠ABC=∠CDF′,∴∠ADC+∠CDF′=180°,即∠ADF′为平角,∴A,D,F′共线,
∵∴∠BCF+∠ECD=∠ECF=∠BCD,
∵FC=F′C,EC=EC,∠ECF'=∠BCF+∠DCE=∠ECF,∴△FCE≌△F′CE,∴EF′=EF=DF′+ED,∴BF=EF -ED;
(2)∵AB=BC,∠B=80°,∴∠ACB=50°,由(1)得∠FEC=∠DEC=70°,
又∵AD//BC,∴∠ECB=70°,而∠B=∠BCD=80°,
∴∠DCE=10°,∴∠BCF=30°,∴∠ACF=∠BCA -∠BCF=20°.
23.(1)解:上面的结论还成立,理由如下:
如图,在的延长线上,截取,连接,
在和中, ,∴,∴,,
∵,,∴,∴,∴,
在和中,,∴,∴,
∵,∴;
(2)解:,理由如下:如图,在上截取,连接
在和中,,∴,
∴,,∴ ,即,
∵,∴
在和中,,∴,
∴,∴,∴;
(3)解:∵ ,∴,
∴的面积,∴的面积为,故答案为:.
24.(1)延长至点F,使,连接,
由题意得,,,∴,
∴,∴,
∵,∴,∴,.
∵,,∴,∴,
∵,∴,∴,∴平分.
(2)∵,∴.∵,∴.
∴的周长为:.
(3)延长交于P,延长交于Q,令,连接,
∵是等腰三角形,且,∴,,,
∵△ABC是等边三角形,∴,
∴,,,∴,,
在和中, ,∴ ,∴,,
∵ ,,∴,
在和中, ∴ ,∴,,
∵ ,,∴,∴即,
在和中, ,∴ ,∴.
∴的周长为:.
25.解:(1)如图1,延长到G,使,连接,
∵∴
∴,∴∴.
∵,∴△AEF≌△AEG.∴.
∵.∴;故答案为:;
(2)(1)中的结论仍然成立.
理由是:如图2,延长到G,使,连接
∵,∴
∵∴∴,
∴∴.
∵,∴△AEF≌△AEG.∴.∵.∴;
(3)若如图1,则结论成立,若如图3,则或
证明:在上截取,使,连接.
∵,∴.
∵∴∴
∴.∴
∵,∴△AEF≌△AEG∴.∵∴.同理可得:
∵∴.故答案为:或或.
题型六:对角互补模型
26.A
【详解】解:过点P作PK⊥AB,垂足为点K.∵PK⊥AB,PD⊥BC,∠ABP=∠CBP,∴PK=PD,
在Rt△BPK和Rt△BPD中,,∴Rt△BPK≌Rt△BPD(HL),∴BK=BD,
∵∠APC+∠ABC=180°,且∠ABC+∠KPD=180°,∴∠KPD=∠APC,∴∠APK=∠CPD,故①正确,
在△PAK和△PCD中,,∴△PAK≌△PCD(ASA),∴AK=CD,PA=PC,故②正确,
∴BK﹣AB=BC﹣BD,∴BD﹣AB=BC﹣BD,∴AB+BC=2BD,故③正确,
∵Rt△BPK≌Rt△BPD,△PAK≌△PCD(ASA),∴S△BPK=S△BPD,S△APK=S△PDC,
∴S四边形ABCP=S四边形KBDP=2S△PBD.故④正确.故选A.
27.(1)解:因为,,根据角的内部到角的两边距离相等的点,都在这个角的平分线上,所以点A在的角平分线上
故答案为:角的内部到角的两边距离相等的点,都在这个角的平分线上.
(2)结论:平分仍然成立;
证明:如解图3,过点A作,,∴,
又∵,∴,∴,
又∵,∴,
在和中,∴∴,
又∵,,∴平分,故(1)结论正确.
28.(1)∵OM是∠AOB的角平分线,∴∠AOC=∠BOC=∠AOB=60°,
∵CD⊥OA,∴∠ODC=90°,∴∠OCD=30°,∴∠OCE=∠DCE﹣∠OCD=30°,
在Rt△OCD中,OD=OC,同理:OE=OC,∴OD+OE=OC,
(2)(1)中结论仍然成立,理由:过点C作CF⊥OA于F,CG⊥OB于G,如图,
∴∠OFC=∠OGC=90°,∵∠AOB=120°,∴∠FCG=60°,
同(1)的方法得,OF=OC,OG=OC,∴OF+OG=OC,
∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,∴CF=CG,
∵∠DCE=60°,∠FCG=60°,∴∠DCF=∠ECG,∴△CFD≌△CGE,∴DF=EG,
∴OF=OD+DF=OD+EG,OG=OE﹣EG, ∴OF+OG=OD+EG+OE﹣EG=OD+OE,∴OD+OE=OC;
(3)(1)中结论不成立,结论为:OE﹣OD=OC,理由:过点C作CF⊥OA于F,CG⊥OB于G,如图,
∴∠OFC=∠OGC=90°,∵∠AOB=120°,∴∠FCG=60°,同(1)的方法得,OF=OC,OG=OC,∴OF+OG=OC,
∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,∴CF=CG,
∵∠DCE=60°,∠FCG=60°,∴∠DCF=∠ECG,∴△CFD≌△CGE,
∴DF=EG,∴OF=DF﹣OD=EG﹣OD,OG=OE﹣EG,
∴OF+OG=EG﹣OD+OE﹣EG=OE﹣OD,∴OE﹣OD=OC.
29.解:(1)如图1中,
∵AB=AC,∠A=60°,∴△ABC是等边三角形,∴∠B=∠C=60°,BC=AC=AB=4,
∵点D是线段BC的中点,∴BD=DC=BC=2,∵DF⊥AC,即∠CFD=90°,∴∠CDF=30°,
又∵∠EDF=120°,∴∠EDB=30°,∴∠BED=90°∴BE=BD=1.
(2)如图2中,过点D作DM⊥AB于M,作DN⊥AC于N.
∵∠B=∠C=60°,BD=DC,∠BDM=∠CDN=30°,∴△BDM≌△CDN,∴BM=CN,DM=DN,
又∵∠EDF=120°=∠MDN,∴∠EDM=∠NDF,
又∵∠EMD=∠FND=90°,∴△EDM≌△FDN,∴ME=NF,∴BE+CF=BM+EM+NC﹣FN=2BM=BD=AB.
(3)结论不成立.结论:BE﹣CF=AB.
∵∠B=∠C=60°,BD=DC,∠BDM=∠CDN=30°,∴△BDM≌△CDN,∴BM=CN,DM=DN,
又∵∠EDF=120°=∠MDN,∴∠EDM=∠NDF,
又∵∠EMD=∠FND=90°,∴△EDM≌△FDN,∴ME=NF,∴BE﹣CF=BM+EM﹣(FN﹣CN)=2BM=BD=AB.
30.(1)解:.理由:过点作于点,
∵点在的角平分线上,且于,,∴,,
∵,∴,,∴,
在和中,,∴(),∴.
(2)解:结论:,理由如下:如图,过点作于点,
同(),可证,,∴,
∵,∴,∴,∴,∴.
(3)解:,理由如下:如图,过点作于点,
同(),可证,,∴,
∵,∴,∴,∴,∴.
题型七:角平分线的全等模型(三类)
31.3
【详解】解:如下图,延长交于点,
∵,,,∴,
∵平分,∴,∵,∴,
在和中,,∴,
∴,,∴,∴.故答案为:3.
32.B
【详解】解:如图,在上截取,连接
平分,平分,,
,,,
,,
在和中,,,
,,,
在和中,,,
,,
周长为,,,
,.故选:B.
33.()如图, 延长交于点,由已知可知,∴,
∵,∴;
(),证明如下:如图,延长交于点,则,
∵,∴,∵,∴,
又∵,∴,∴,由已知可知,,∴;
()如图,延长交于,由已知可知,,,∴,
∵,∴,∴.
34.(1)证明:,,,
是的平分线,,
在和中,,,;
(2)证明:如图②,过点作于,于,
是的平分线,,,,
,,,
在和中,,,.
35.(1)证明:射线平分,,
又,,,,故答案为:;
(2)证明:在上截取,连接,如图2所示:
平分,,又,,
,,,,,,
又,,,,,
,;
(3)解:在上取点,使,连接,在上取点,使,连接,如图3所示:
是边的中点,,,
平分,,又,,
,,.同理可证:,
,,,,,
,,,
,是等边三角形,,.
同课章节目录
