人教版八年级数学上册第13章三角形13.2.1三角形的边 课件(共18张PPT)
文档属性
| 名称 | 人教版八年级数学上册第13章三角形13.2.1三角形的边 课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 21:02:25 | ||
图片预览






文档简介
(共18张PPT)
1.掌握三角形的三边关系.
2.熟悉三角形的稳定性在生活中的应用.
3.运用三角形三边关系解决有关的问题.
运用三角形三边关系解决有关的问题.
掌握三角形的三边关系.
难点
重点
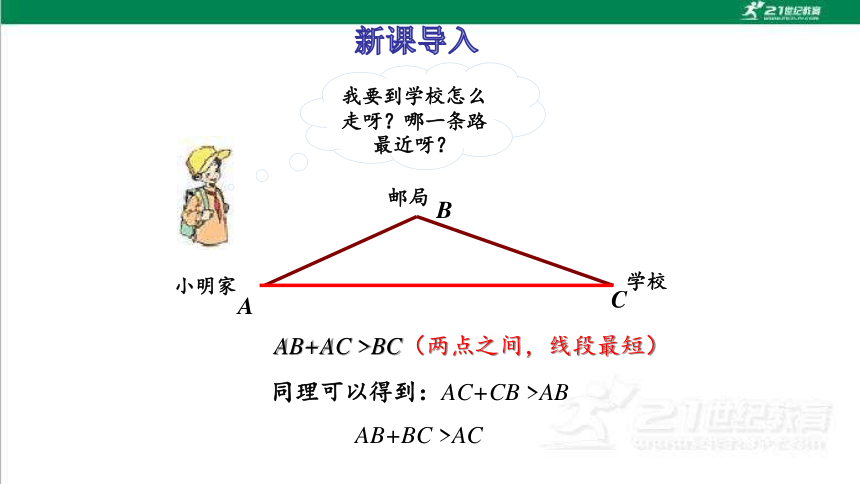
我要到学校怎么走呀?哪一条路最近呀?
邮局
学校
小明家
A
C
B
AB+AC >BC(两点之间,线段最短)
同理可以得到:AC+CB >AB
AB+BC >AC
归纳总结
1.在同一个三角形中,任意两边之和与第三边有什么大小关系
2.在同一个三角形中,任意两边之差与第三边有什么大小关系
3.三角形三边有怎样的不等关系
通过动手实验同学们可以得到哪些结论 理由是什么?
议一议
归纳总结
上面的结论表明了三角形三边之间的关系.反过来,对于三条线段,当它们满足什么条件时,这三条线段能组成三角形?
思考
1.以下列各组线段为边,能组成三角形的是( )
A.1,2,3 B.1,3,5
C.2,3,4 D.2,6,10
C
2.用一条长为18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
(2)能围成有一边的长是4 cm的等腰三角形吗?为什么?
解:(1)设底边长为x cm,则腰长为2x cm,则x+2x+2x=18.解得x=3.6.
所以,三角形三边的长分别为3.6 cm,7.2 cm,7.2 cm.
(2)因为长为4 cm的边可能是腰,也可能是底边,所以需要分情况讨论.①如果4 cm长的边为底边,设腰长为x cm,则4+2x=18.解得x=7.
②如果4 cm长的边为腰,设底边长为y cm,则2×4+y=18.解得y=10.
因为4+4<10,不符合“三角形两边的和大于第三边”,所以不能围成腰长是4 cm的等腰三角形.
由以上讨论可知,可以围成底边长是4 cm的等腰三角形.
3.有两根长度分别为5cm和8cm的木棒,
(1)用长度为2cm的木棒与它们能摆成三角形吗?为什么?长度为13cm的木棒呢?
(2)如果一根木棒能与原来的两根木棒摆成三角形,那么它的长度取值范围是什么?
解:(1)取长度为2cm的木棒时,由于2+5=7<8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.取长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
(2)3cm<第三边<13cm
工程建筑中经常采用三角形的结构,如屋顶钢架(图(1)),其 中的道理是什么?盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条(图(2)). 为什么要这样做呢?
问题探究
如图,将三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
三角形具有稳定性.
不会
归纳总结
4.下列图形中哪些具有稳定性.
具有稳定性
不具有稳定性
不具有稳定性
具有稳定性
不具有稳定性
具有稳定性
5.下列图形中具有稳定性的是( )
A.①②③④ B.①③
C.②④ D.①②③
B
你能举出一些现实生活中的应用了三角形稳定性的例子吗?
三角形
三边关系
原理
两点之间,线段最短
内容
两边之和大于第三边
两边之差小于第三边
应用
稳定性
2.已知三角形两边长分别为4和8,则该三角形第三边的长可能是( )
A.4 B.5 C.12 D.13
B
1.下列长度的三条线段能组成三角形的是( )
A.3,3,6 B.3,5,10 C.4,6,9 D.4,5,9
C
3.如图,桥梁的斜拉钢索是三角形的结构,主要是为了( )
A.节省材料,节约成本
B.保持对称
C.利用三角形的稳定性
D.美观漂亮
C
4.如图所示,建高楼常需要用塔吊来吊建筑材料,而塔吊的上部是三角形结构,这是应用了三角形的哪个性质?答:________.(填“稳定性”或“不稳定性”)
稳定性
1.掌握三角形的三边关系.
2.熟悉三角形的稳定性在生活中的应用.
3.运用三角形三边关系解决有关的问题.
运用三角形三边关系解决有关的问题.
掌握三角形的三边关系.
难点
重点
我要到学校怎么走呀?哪一条路最近呀?
邮局
学校
小明家
A
C
B
AB+AC >BC(两点之间,线段最短)
同理可以得到:AC+CB >AB
AB+BC >AC
归纳总结
1.在同一个三角形中,任意两边之和与第三边有什么大小关系
2.在同一个三角形中,任意两边之差与第三边有什么大小关系
3.三角形三边有怎样的不等关系
通过动手实验同学们可以得到哪些结论 理由是什么?
议一议
归纳总结
上面的结论表明了三角形三边之间的关系.反过来,对于三条线段,当它们满足什么条件时,这三条线段能组成三角形?
思考
1.以下列各组线段为边,能组成三角形的是( )
A.1,2,3 B.1,3,5
C.2,3,4 D.2,6,10
C
2.用一条长为18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
(2)能围成有一边的长是4 cm的等腰三角形吗?为什么?
解:(1)设底边长为x cm,则腰长为2x cm,则x+2x+2x=18.解得x=3.6.
所以,三角形三边的长分别为3.6 cm,7.2 cm,7.2 cm.
(2)因为长为4 cm的边可能是腰,也可能是底边,所以需要分情况讨论.①如果4 cm长的边为底边,设腰长为x cm,则4+2x=18.解得x=7.
②如果4 cm长的边为腰,设底边长为y cm,则2×4+y=18.解得y=10.
因为4+4<10,不符合“三角形两边的和大于第三边”,所以不能围成腰长是4 cm的等腰三角形.
由以上讨论可知,可以围成底边长是4 cm的等腰三角形.
3.有两根长度分别为5cm和8cm的木棒,
(1)用长度为2cm的木棒与它们能摆成三角形吗?为什么?长度为13cm的木棒呢?
(2)如果一根木棒能与原来的两根木棒摆成三角形,那么它的长度取值范围是什么?
解:(1)取长度为2cm的木棒时,由于2+5=7<8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.取长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
(2)3cm<第三边<13cm
工程建筑中经常采用三角形的结构,如屋顶钢架(图(1)),其 中的道理是什么?盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条(图(2)). 为什么要这样做呢?
问题探究
如图,将三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
三角形具有稳定性.
不会
归纳总结
4.下列图形中哪些具有稳定性.
具有稳定性
不具有稳定性
不具有稳定性
具有稳定性
不具有稳定性
具有稳定性
5.下列图形中具有稳定性的是( )
A.①②③④ B.①③
C.②④ D.①②③
B
你能举出一些现实生活中的应用了三角形稳定性的例子吗?
三角形
三边关系
原理
两点之间,线段最短
内容
两边之和大于第三边
两边之差小于第三边
应用
稳定性
2.已知三角形两边长分别为4和8,则该三角形第三边的长可能是( )
A.4 B.5 C.12 D.13
B
1.下列长度的三条线段能组成三角形的是( )
A.3,3,6 B.3,5,10 C.4,6,9 D.4,5,9
C
3.如图,桥梁的斜拉钢索是三角形的结构,主要是为了( )
A.节省材料,节约成本
B.保持对称
C.利用三角形的稳定性
D.美观漂亮
C
4.如图所示,建高楼常需要用塔吊来吊建筑材料,而塔吊的上部是三角形结构,这是应用了三角形的哪个性质?答:________.(填“稳定性”或“不稳定性”)
稳定性
同课章节目录
