人教版八年级数学上册 13.3.2三角形的外角 课件(共18张PPT)
文档属性
| 名称 | 人教版八年级数学上册 13.3.2三角形的外角 课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 14:26:21 | ||
图片预览



文档简介
(共18张PPT)
1.了解三角形的外角的概念.
2.理解三角形的外角性质.
3.熟练掌握并运用三角形外角性质解决实际问题.
理解三角形的外角性质.
熟练掌握并运用三角形的外角性质解决实际问题.
难点
重点
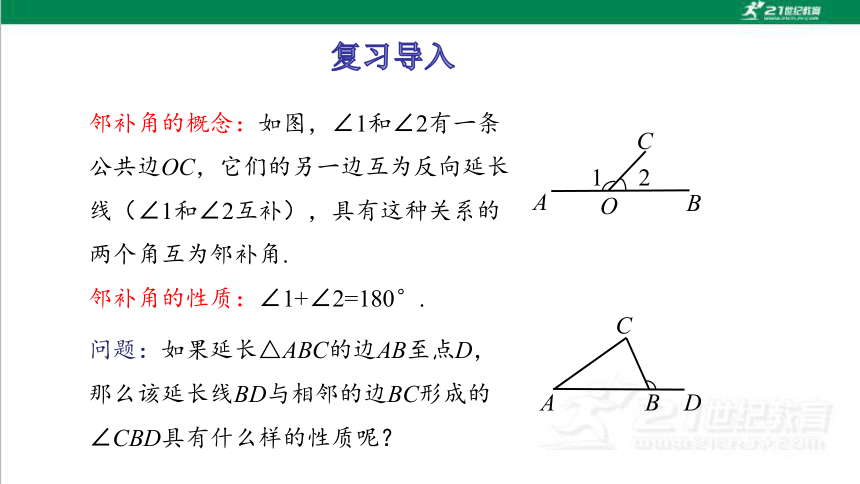
邻补角的概念:如图,∠1和∠2有一条公共边OC,它们的另一边互为反向延长线(∠1和∠2互补),具有这种关系的两个角互为邻补角.
邻补角的性质:∠1+∠2=180°.
C
A
B
O
1
2
问题:如果延长△ABC的边AB至点D,那么该延长线BD与相邻的边BC形成的∠CBD具有什么样的性质呢?
B
C
A
D
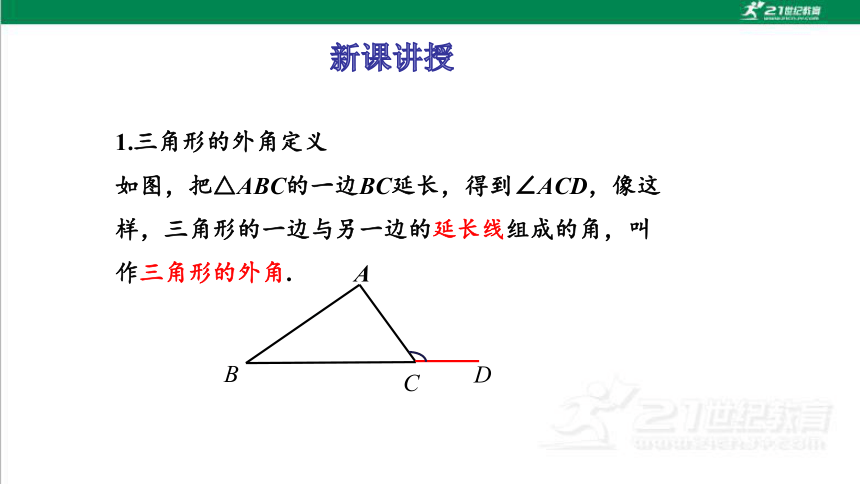
1.三角形的外角定义
如图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫作三角形的外角.
A
C
B
D
问题1:三角形的外角和相邻的内角之间的大小关系?
问题2:三角形的外角具备什么特征?
三角形的外角和相邻的内角之和为180°.
①顶点在三角形的一个顶点上;
②一条边是三角形的一条边;
③另外一条边是三角形某条边的延长线.
A
B
C
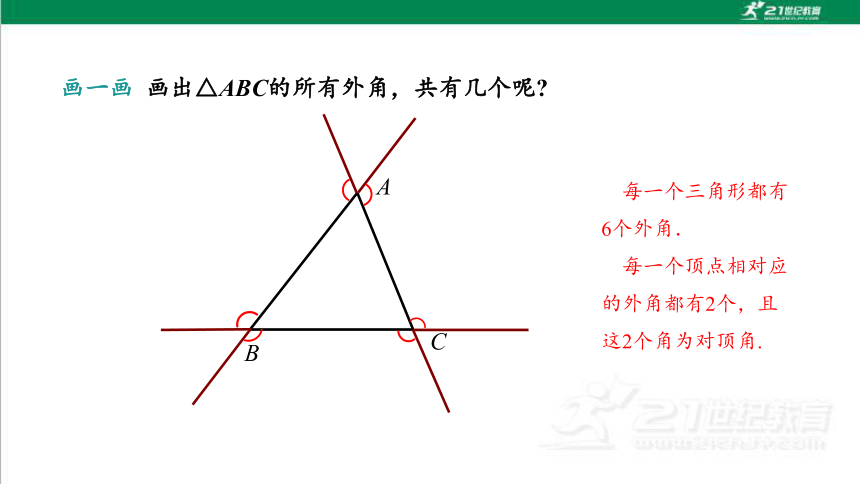
画一画 画出△ABC的所有外角,共有几个呢
每一个三角形都有6个外角.
每一个顶点相对应的外角都有2个,且这2个角为对顶角.
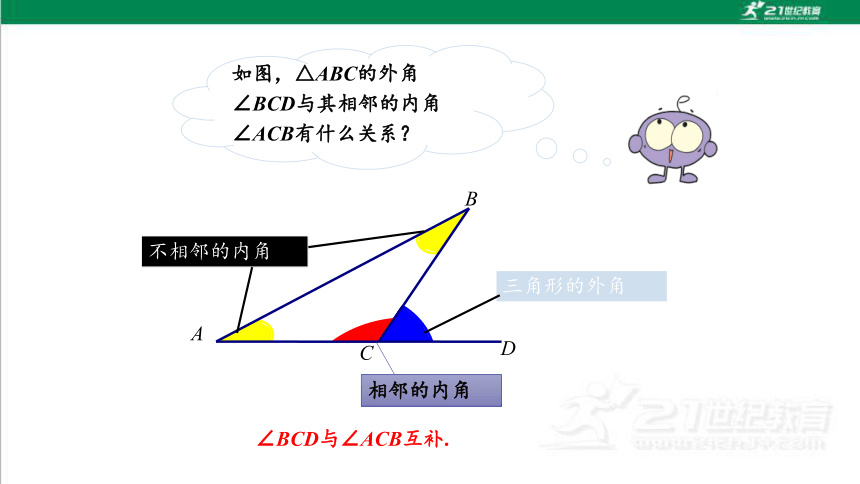
如图,△ABC的外角∠BCD与其相邻的内角∠ACB有什么关系?
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
∠BCD与∠ACB互补.
如图,△ABC的外角∠BCD与其与其不相邻的两内角(∠A,∠B)有什么关系?
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
∵∠A+∠B+∠ACB=180°,∠BCD+∠ACB=180°,
∴∠A+∠B=∠BCD.
D
证明:过C作CE平行于AB,
A
B
C
1
2
∴∠1= ∠B,(两直线平行,同位角相等)
∠2= ∠A ,(两直线平行,内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B.
E
已知:如图,△ABC,求证:∠ACD=∠A+∠B.
验证结论
2.三角形的内角和定理的推论
三角形的外角等于与它不相邻的两个内角的和.
1.图中∠1的大小等于( )
A.40°
B.50°
C.60°
D.70°
D
2.如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )
A.40° B.45° C.50° D.55°
解析:∵∠A=60°,∠B=40°,
∴∠ACD=∠A+∠B=100°.
∵CE平分∠ACD,
∴∠ECD=50°.
A
B
C
D
E
C
3.如图,∠A=42°,∠ABD=28°,∠ACE=18°,求∠BFC的度数.
∵ ∠BEC是△AEC的一个外角,
∴ ∠BEC= ∠A+ ∠ACE,
∵∠A=42°,∠ACE=18°,
∴ ∠BEC=60°.
∵ ∠BFC是△BEF的一个外角,
∴ ∠BFC= ∠ABD+ ∠BEF,
∵ ∠ABD=28° ,∠BEC=60°,
∴ ∠BFC=88°.
解:
F
A
C
D
E
B
4.如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角,它们的和是多少?
解:由三角形的一个外角等于与它不相邻的两个内角的和,得∠BAE=∠2+∠3,∠CBF=∠1+∠3,∠ACD=∠1+∠2.
所以∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3).
由∠1+∠2+∠3=180°,得
∠BAE+∠CBF+∠ACD=2×180°=360°.
三角形的外角
定义
角一边必须是三角形的一边,另一边必须是三角形另一边的延长线
性质
三角形的外角等于与它不相邻的两个内角的和
1.如图,∠A,∠1,∠2的大小关系是( )
A.∠A>∠1>∠2
B.∠2>∠1>∠A
C.∠A>∠2>∠1
D.∠2>∠A>∠1
B
2.如图,AB//CD,∠A=37°, ∠C=63°,那么∠F等于( )
F
A
B
E
C
D
A.26°
B.63°
C.37°
D.60°
A
解:∵∠ADC是△ABD的外角.
3.如图,D是△ABC的BC边上一点,∠B=∠BAD, ∠ADC=80°,∠BAC=70°,求:(1)∠B 的度数;(2)∠C的度数.
在△ABC中,
∠B+∠BAC+∠C=180°,
∠C=180 -40 -70 =70°.
∴∠ADC=∠B+∠BAD=80°.
又∵∠B=∠BAD,
A
B
C
D
1.了解三角形的外角的概念.
2.理解三角形的外角性质.
3.熟练掌握并运用三角形外角性质解决实际问题.
理解三角形的外角性质.
熟练掌握并运用三角形的外角性质解决实际问题.
难点
重点
邻补角的概念:如图,∠1和∠2有一条公共边OC,它们的另一边互为反向延长线(∠1和∠2互补),具有这种关系的两个角互为邻补角.
邻补角的性质:∠1+∠2=180°.
C
A
B
O
1
2
问题:如果延长△ABC的边AB至点D,那么该延长线BD与相邻的边BC形成的∠CBD具有什么样的性质呢?
B
C
A
D
1.三角形的外角定义
如图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫作三角形的外角.
A
C
B
D
问题1:三角形的外角和相邻的内角之间的大小关系?
问题2:三角形的外角具备什么特征?
三角形的外角和相邻的内角之和为180°.
①顶点在三角形的一个顶点上;
②一条边是三角形的一条边;
③另外一条边是三角形某条边的延长线.
A
B
C
画一画 画出△ABC的所有外角,共有几个呢
每一个三角形都有6个外角.
每一个顶点相对应的外角都有2个,且这2个角为对顶角.
如图,△ABC的外角∠BCD与其相邻的内角∠ACB有什么关系?
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
∠BCD与∠ACB互补.
如图,△ABC的外角∠BCD与其与其不相邻的两内角(∠A,∠B)有什么关系?
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
∵∠A+∠B+∠ACB=180°,∠BCD+∠ACB=180°,
∴∠A+∠B=∠BCD.
D
证明:过C作CE平行于AB,
A
B
C
1
2
∴∠1= ∠B,(两直线平行,同位角相等)
∠2= ∠A ,(两直线平行,内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B.
E
已知:如图,△ABC,求证:∠ACD=∠A+∠B.
验证结论
2.三角形的内角和定理的推论
三角形的外角等于与它不相邻的两个内角的和.
1.图中∠1的大小等于( )
A.40°
B.50°
C.60°
D.70°
D
2.如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )
A.40° B.45° C.50° D.55°
解析:∵∠A=60°,∠B=40°,
∴∠ACD=∠A+∠B=100°.
∵CE平分∠ACD,
∴∠ECD=50°.
A
B
C
D
E
C
3.如图,∠A=42°,∠ABD=28°,∠ACE=18°,求∠BFC的度数.
∵ ∠BEC是△AEC的一个外角,
∴ ∠BEC= ∠A+ ∠ACE,
∵∠A=42°,∠ACE=18°,
∴ ∠BEC=60°.
∵ ∠BFC是△BEF的一个外角,
∴ ∠BFC= ∠ABD+ ∠BEF,
∵ ∠ABD=28° ,∠BEC=60°,
∴ ∠BFC=88°.
解:
F
A
C
D
E
B
4.如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角,它们的和是多少?
解:由三角形的一个外角等于与它不相邻的两个内角的和,得∠BAE=∠2+∠3,∠CBF=∠1+∠3,∠ACD=∠1+∠2.
所以∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3).
由∠1+∠2+∠3=180°,得
∠BAE+∠CBF+∠ACD=2×180°=360°.
三角形的外角
定义
角一边必须是三角形的一边,另一边必须是三角形另一边的延长线
性质
三角形的外角等于与它不相邻的两个内角的和
1.如图,∠A,∠1,∠2的大小关系是( )
A.∠A>∠1>∠2
B.∠2>∠1>∠A
C.∠A>∠2>∠1
D.∠2>∠A>∠1
B
2.如图,AB//CD,∠A=37°, ∠C=63°,那么∠F等于( )
F
A
B
E
C
D
A.26°
B.63°
C.37°
D.60°
A
解:∵∠ADC是△ABD的外角.
3.如图,D是△ABC的BC边上一点,∠B=∠BAD, ∠ADC=80°,∠BAC=70°,求:(1)∠B 的度数;(2)∠C的度数.
在△ABC中,
∠B+∠BAC+∠C=180°,
∠C=180 -40 -70 =70°.
∴∠ADC=∠B+∠BAD=80°.
又∵∠B=∠BAD,
A
B
C
D
同课章节目录
