人教版八年级数学上册第14章全等三角形14.2三角形全等的判定第3课时三边证全等 课件(共16张PPT)
文档属性
| 名称 | 人教版八年级数学上册第14章全等三角形14.2三角形全等的判定第3课时三边证全等 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
1.理解并掌握三角形全等判定“边边边”条件的内容.
2.熟练利用“边边边”条件证明两个三角形全等.
3.通过探究判定三角形全等条件的过程,提高分析和解决问题的能力.
理解并掌握三角形全等判定“边边边”条件的内容.
熟练利用“边边边”条件证明两个三角形全等.
难点
重点
当两个三角形满足6个条件中的3个时,有4种情况:
两边一角 SAS√
SSA×
两角一边 AAS√
ASA√
三边 ?
三角 ?
除了SAS、AAS及ASA外,还有其他情况可以判定三角形全等吗?
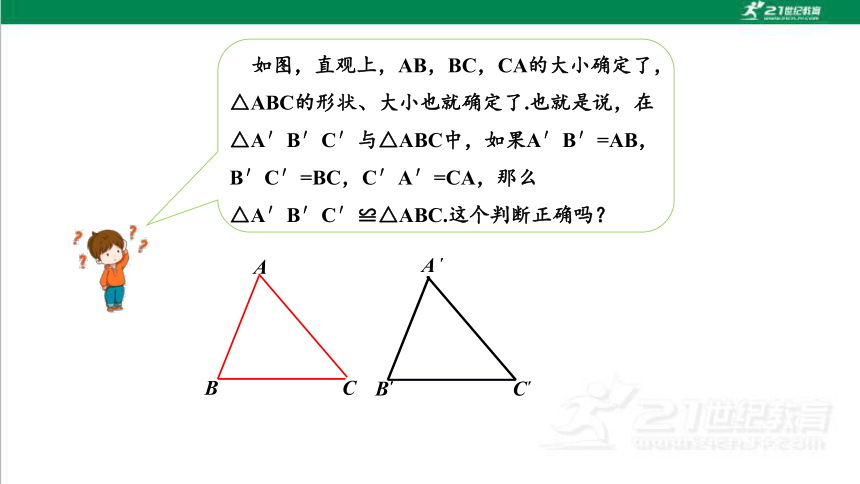
如图,直观上,AB,BC,CA的大小确定了,△ABC的形状、大小也就确定了.也就是说,在△A′B′C′与△ABC中,如果A′B′=AB,B′C′=BC,C′A′=CA,那么△A′B′C′≌△ABC.这个判断正确吗?
A
B
C
A ′
B′
C′
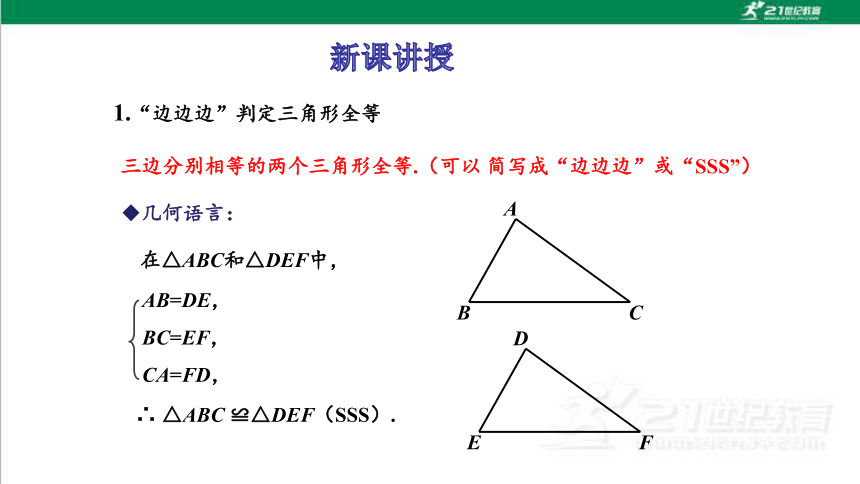
1.“边边边”判定三角形全等
三边分别相等的两个三角形全等.(可以 简写成“边边边”或“SSS”)
A
B
C
D
E
F
在△ABC和△DEF中,
∴ △ABC ≌△DEF(SSS).
AB=DE,
BC=EF,
CA=FD,
几何语言:
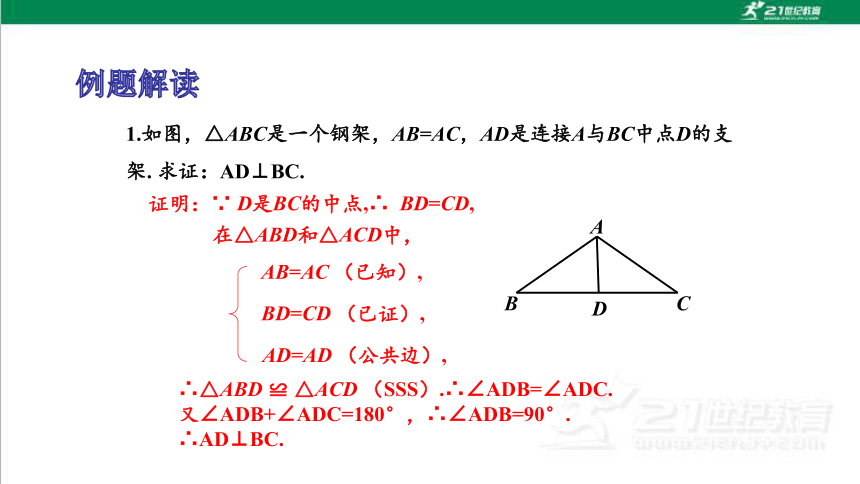
1.如图,△ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架. 求证:AD⊥BC.
D
B
C
A
在△ABD和△ACD中,
AB=AC (已知),
BD=CD (已证),
AD=AD (公共边),
∴△ABD ≌ △ACD (SSS).∴∠ADB=∠ADC.
又∠ADB+∠ADC=180°,∴∠ADB=90°.
∴AD⊥BC.
证明:∵ D是BC的中点,∴ BD=CD,
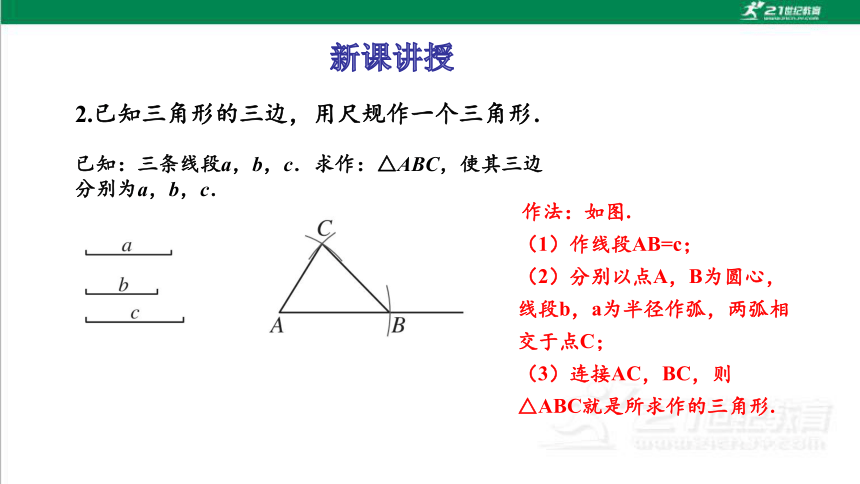
2.已知三角形的三边,用尺规作一个三角形.
已知:三条线段a,b,c.求作:△ABC,使其三边分别为a,b,c.
作法:如图.
(1)作线段AB=c;
(2)分别以点A,B为圆心,线段b,a为半径作弧,两弧相交于点C;
(3)连接AC,BC,则△ABC就是所求作的三角形.
2.工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别截取OM=ON.移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线,为什么?
证明:在△MOC和△NOC中,
∴△MOC≌△NOC(SSS).
∴∠MOC=∠NOC,则OC是∠AOB的平分线.
A
M
C
N
B
O
OM=ON,
OC=OC,
CM=CN,
我们探究完了通过“两边一角”“两角一边”“三边”判定两个三角形全等的情况,还剩下最后一种,即通过“三角”能不能判定两个三角形全等呢?
不能
下图中,DE∥BC,则∠ADE=∠B,∠AED=∠C,又∠A=∠A,但显然△ABC和△ADE不全等.
边边边
三角形全等的判定
边角边
角边角
角角边
边边边
1.如图,下列三角形中,与△ABC全等的是( )
C
2.如图,已知AC=FE,BC=DE,点A,D,B,F 在一条直线上,要利用“SSS”证明△ABC≌△FDE,还可以添加的一个条件是( )
A.AD=FB B.DE=BD
C.BF=DB D.以上都不对
A
3.如图, C是BF的中点,AB=DC,AC=DF.
求证:△ABC ≌ △DCF.
在△ABC 和△DCF中,
AB = DC,
∴ △ABC ≌ △DCF
AC = DF,
BC = CF,
证明:∵C是BF中点,
∴BC=CF.
(SSS).
4.已知:如图 ,AC=FE,AD=FB,BC=DE.
求证:(1)△ABC≌△FDE; (2) ∠C= ∠E.
证明:(1)∵ AD=FB,
∴AB=FD.
在△ABC和△FDE 中,
AC=FE,
BC=DE,
AB=FD,
∴△ABC≌△FDE(SSS).
A
C
E
D
B
F
=
=
。
。
(2)∵ △ABC≌△FDE.
∴ ∠C=∠E.
1.理解并掌握三角形全等判定“边边边”条件的内容.
2.熟练利用“边边边”条件证明两个三角形全等.
3.通过探究判定三角形全等条件的过程,提高分析和解决问题的能力.
理解并掌握三角形全等判定“边边边”条件的内容.
熟练利用“边边边”条件证明两个三角形全等.
难点
重点
当两个三角形满足6个条件中的3个时,有4种情况:
两边一角 SAS√
SSA×
两角一边 AAS√
ASA√
三边 ?
三角 ?
除了SAS、AAS及ASA外,还有其他情况可以判定三角形全等吗?
如图,直观上,AB,BC,CA的大小确定了,△ABC的形状、大小也就确定了.也就是说,在△A′B′C′与△ABC中,如果A′B′=AB,B′C′=BC,C′A′=CA,那么△A′B′C′≌△ABC.这个判断正确吗?
A
B
C
A ′
B′
C′
1.“边边边”判定三角形全等
三边分别相等的两个三角形全等.(可以 简写成“边边边”或“SSS”)
A
B
C
D
E
F
在△ABC和△DEF中,
∴ △ABC ≌△DEF(SSS).
AB=DE,
BC=EF,
CA=FD,
几何语言:
1.如图,△ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架. 求证:AD⊥BC.
D
B
C
A
在△ABD和△ACD中,
AB=AC (已知),
BD=CD (已证),
AD=AD (公共边),
∴△ABD ≌ △ACD (SSS).∴∠ADB=∠ADC.
又∠ADB+∠ADC=180°,∴∠ADB=90°.
∴AD⊥BC.
证明:∵ D是BC的中点,∴ BD=CD,
2.已知三角形的三边,用尺规作一个三角形.
已知:三条线段a,b,c.求作:△ABC,使其三边分别为a,b,c.
作法:如图.
(1)作线段AB=c;
(2)分别以点A,B为圆心,线段b,a为半径作弧,两弧相交于点C;
(3)连接AC,BC,则△ABC就是所求作的三角形.
2.工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别截取OM=ON.移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线,为什么?
证明:在△MOC和△NOC中,
∴△MOC≌△NOC(SSS).
∴∠MOC=∠NOC,则OC是∠AOB的平分线.
A
M
C
N
B
O
OM=ON,
OC=OC,
CM=CN,
我们探究完了通过“两边一角”“两角一边”“三边”判定两个三角形全等的情况,还剩下最后一种,即通过“三角”能不能判定两个三角形全等呢?
不能
下图中,DE∥BC,则∠ADE=∠B,∠AED=∠C,又∠A=∠A,但显然△ABC和△ADE不全等.
边边边
三角形全等的判定
边角边
角边角
角角边
边边边
1.如图,下列三角形中,与△ABC全等的是( )
C
2.如图,已知AC=FE,BC=DE,点A,D,B,F 在一条直线上,要利用“SSS”证明△ABC≌△FDE,还可以添加的一个条件是( )
A.AD=FB B.DE=BD
C.BF=DB D.以上都不对
A
3.如图, C是BF的中点,AB=DC,AC=DF.
求证:△ABC ≌ △DCF.
在△ABC 和△DCF中,
AB = DC,
∴ △ABC ≌ △DCF
AC = DF,
BC = CF,
证明:∵C是BF中点,
∴BC=CF.
(SSS).
4.已知:如图 ,AC=FE,AD=FB,BC=DE.
求证:(1)△ABC≌△FDE; (2) ∠C= ∠E.
证明:(1)∵ AD=FB,
∴AB=FD.
在△ABC和△FDE 中,
AC=FE,
BC=DE,
AB=FD,
∴△ABC≌△FDE(SSS).
A
C
E
D
B
F
=
=
。
。
(2)∵ △ABC≌△FDE.
∴ ∠C=∠E.
同课章节目录
