人教版八年级数学上册第14章全等三角形14.2三角形全等的判定第1课时两边及其夹角证全等 课件(共18张PPT)
文档属性
| 名称 | 人教版八年级数学上册第14章全等三角形14.2三角形全等的判定第1课时两边及其夹角证全等 课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 21:28:05 | ||
图片预览



文档简介
(共18张PPT)
1.理解并掌握三角形全等判定“边角边”条件的内容.
2.会用“边角边”判定方法证明两个三角形全等及进行简单的应用.
3.了解“边边角”不能作为两个三角形全等的条件.
理解并掌握三角形全等判定“边角边”条件的内容.
了解“边边角”不能作为两个三角形全等的条件.
难点
重点
根据全等三角形的定义,如果△ABC与△A′B′C′满足三条边分别相等,三个角分别相等,即
AB=A′B′,BC=B′C′,CA=C′A′,
∠A=∠A′,∠B=∠B′,∠C=∠C′,
就能判断△ABC≌△A′B′C′.
一定要满足三条边分别相等,三个角也分别相等,才能保证两个三角形全等吗?
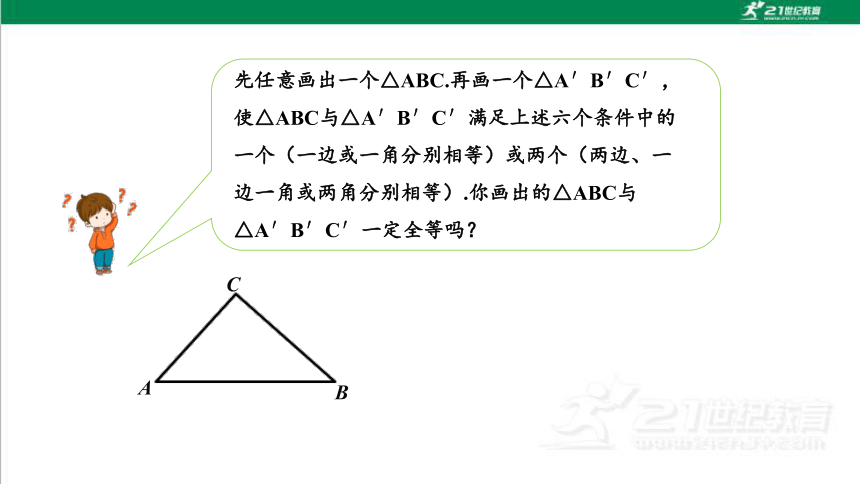
先任意画出一个△ABC.再画一个△A′B′C′,使△ABC与△A′B′C′满足上述六个条件中的一个(一边或一角分别相等)或两个(两边、一边一角或两角分别相等).你画出的△ABC与△A′B′C′一定全等吗?
A
B
C
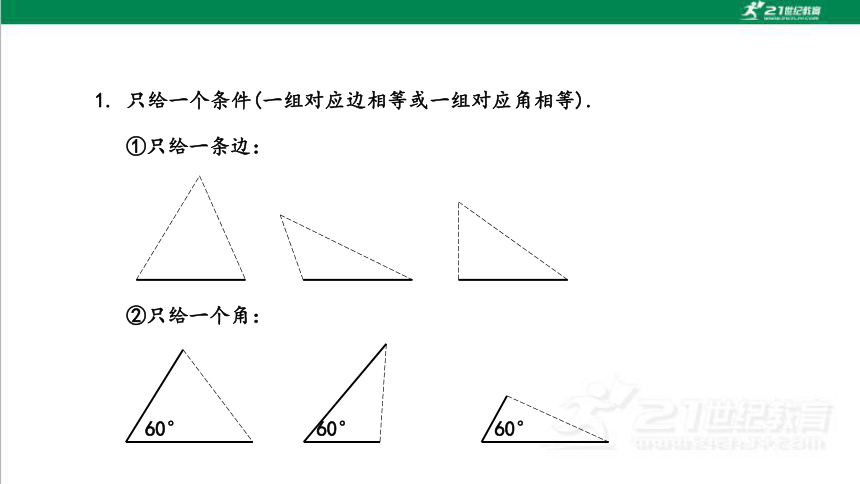
1. 只给一个条件(一组对应边相等或一组对应角相等).
①只给一条边:
②只给一个角:
60°
60°
60°
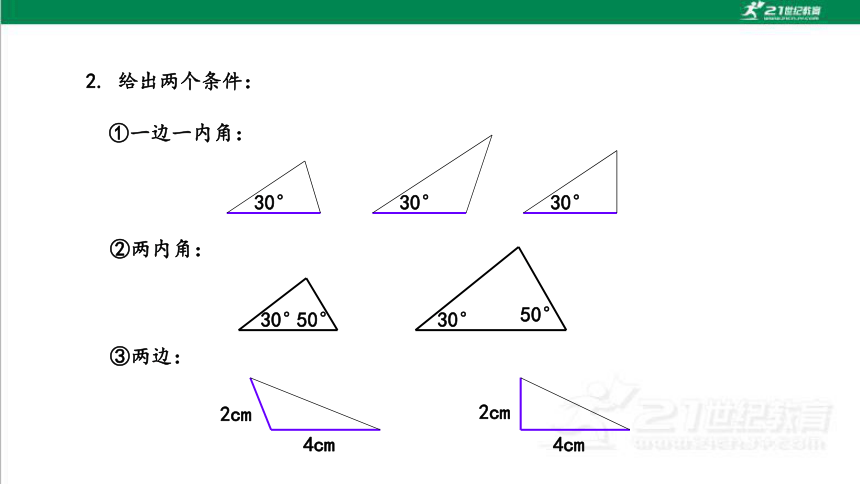
2. 给出两个条件:
①一边一内角:
30°
30°
30°
②两内角:
30°
30°
50°
50°
③两边:
2cm
2cm
4cm
4cm
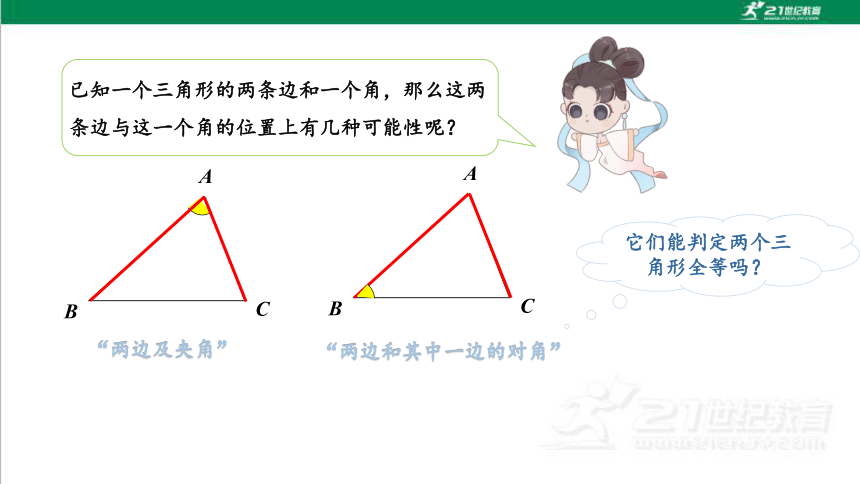
已知一个三角形的两条边和一个角,那么这两条边与这一个角的位置上有几种可能性呢?
A
B
C
A
B
C
它们能判定两个三角形全等吗?
如图,直观上,如果∠A,AB,AC的大小确定了,△ABC的形状、大小也就确定了.也就是说,在△A′B′C′与△ABC中,如果∠A′=∠A,A′B′=AB,A′C′=AC,那么△A′B′C′≌△ABC.这个判断正确吗?
1.“边角边”判定三角形全等
在△ABC 和△DEF中,
∴△ABC ≌△DEF(SAS).
两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”).
几何语言:
AB = DE,
∠A =∠D,
AC =AF ,
A
B
C
D
E
F
必须是两边“夹角”
1.如图,AC=AD,AB平分∠CAD,求证∠C=∠D.
如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC.固定住长木棍,转动短木棍,得到△ABD.这个实验说明了什么?
B
A
C
D
△ABC和△ABD满足AB=AB ,AC=AD,
∠B=∠B,但△ABC与△ABD不全等.
想一想:SSA能否判定两个三角形全等?
2.下列条件中,不能证明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,BC=EF
B.AB=DE,∠A=∠D,AC=DF
C.BC=EF,∠B=∠E,AC=DF
D.BC=EF,∠C=∠F,AC=DF
C
3.如图,点E,F在AC上,AD//BC,AD=CB,AE=CF.
求证:△AFD≌△CEB.
F
A
B
D
C
E
证明:
∵AD//BC,
∴ ∠A=∠C,
∵AE=CF,
在△AFD和△CEB中,
AD=CB,
∠A=∠C,
AF=CE,
∴△AFD≌△CEB(SAS).
∴AE+EF=CF+EF,即AF=CE.
边角边
内容
两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边” 或“SAS”)
注意
“SSA”不能判定三角形全等
1.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增加的条件是( )
A.∠A=∠D B.∠E=∠C
C.∠A=∠C D.∠ABD=∠EBC
D
2.如图,AA′,BB′表示两根长度相同的木条,若O是AA′,BB′的中点,经测量AB=9 cm,则容器的内径A′B′为( )
A.8 cm
B.9 cm
C.10 cm
D.11 cm
B
3.已知:如图, AB=DB,CB=EB,∠1=∠2,求证:∠A=∠D.
证明:∵ ∠1=∠2,
∴∠1+∠DBC=∠2+∠DBC,即∠ABC=∠DBE.
在△ABC和△DBE中,
AB=DB,
∠ABC=∠DBE,
CB=EB,
∴△ABC≌△DBE(SAS).
∴ ∠A=∠D.
1
A
2
C
B
D
E
解:DE=BF,DE//BF.理由如下:
在△ADE和△CBF中,
AD=CB,
∠DAC=∠BCA,
AE=CF,
∴ △ADE≌△CBF(SAS).
∴∠DEA=∠BFC,DE=BF.
∴∠DEC=∠BFE,DE//BF.
4.如图,已知AB=CD,BC=DA,E, F是AC上的两点,且AE=CF,写出DE和BF之间的关系,并证明你的结论.
A
B
D
E
F
C
1.理解并掌握三角形全等判定“边角边”条件的内容.
2.会用“边角边”判定方法证明两个三角形全等及进行简单的应用.
3.了解“边边角”不能作为两个三角形全等的条件.
理解并掌握三角形全等判定“边角边”条件的内容.
了解“边边角”不能作为两个三角形全等的条件.
难点
重点
根据全等三角形的定义,如果△ABC与△A′B′C′满足三条边分别相等,三个角分别相等,即
AB=A′B′,BC=B′C′,CA=C′A′,
∠A=∠A′,∠B=∠B′,∠C=∠C′,
就能判断△ABC≌△A′B′C′.
一定要满足三条边分别相等,三个角也分别相等,才能保证两个三角形全等吗?
先任意画出一个△ABC.再画一个△A′B′C′,使△ABC与△A′B′C′满足上述六个条件中的一个(一边或一角分别相等)或两个(两边、一边一角或两角分别相等).你画出的△ABC与△A′B′C′一定全等吗?
A
B
C
1. 只给一个条件(一组对应边相等或一组对应角相等).
①只给一条边:
②只给一个角:
60°
60°
60°
2. 给出两个条件:
①一边一内角:
30°
30°
30°
②两内角:
30°
30°
50°
50°
③两边:
2cm
2cm
4cm
4cm
已知一个三角形的两条边和一个角,那么这两条边与这一个角的位置上有几种可能性呢?
A
B
C
A
B
C
它们能判定两个三角形全等吗?
如图,直观上,如果∠A,AB,AC的大小确定了,△ABC的形状、大小也就确定了.也就是说,在△A′B′C′与△ABC中,如果∠A′=∠A,A′B′=AB,A′C′=AC,那么△A′B′C′≌△ABC.这个判断正确吗?
1.“边角边”判定三角形全等
在△ABC 和△DEF中,
∴△ABC ≌△DEF(SAS).
两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”).
几何语言:
AB = DE,
∠A =∠D,
AC =AF ,
A
B
C
D
E
F
必须是两边“夹角”
1.如图,AC=AD,AB平分∠CAD,求证∠C=∠D.
如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC.固定住长木棍,转动短木棍,得到△ABD.这个实验说明了什么?
B
A
C
D
△ABC和△ABD满足AB=AB ,AC=AD,
∠B=∠B,但△ABC与△ABD不全等.
想一想:SSA能否判定两个三角形全等?
2.下列条件中,不能证明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,BC=EF
B.AB=DE,∠A=∠D,AC=DF
C.BC=EF,∠B=∠E,AC=DF
D.BC=EF,∠C=∠F,AC=DF
C
3.如图,点E,F在AC上,AD//BC,AD=CB,AE=CF.
求证:△AFD≌△CEB.
F
A
B
D
C
E
证明:
∵AD//BC,
∴ ∠A=∠C,
∵AE=CF,
在△AFD和△CEB中,
AD=CB,
∠A=∠C,
AF=CE,
∴△AFD≌△CEB(SAS).
∴AE+EF=CF+EF,即AF=CE.
边角边
内容
两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边” 或“SAS”)
注意
“SSA”不能判定三角形全等
1.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增加的条件是( )
A.∠A=∠D B.∠E=∠C
C.∠A=∠C D.∠ABD=∠EBC
D
2.如图,AA′,BB′表示两根长度相同的木条,若O是AA′,BB′的中点,经测量AB=9 cm,则容器的内径A′B′为( )
A.8 cm
B.9 cm
C.10 cm
D.11 cm
B
3.已知:如图, AB=DB,CB=EB,∠1=∠2,求证:∠A=∠D.
证明:∵ ∠1=∠2,
∴∠1+∠DBC=∠2+∠DBC,即∠ABC=∠DBE.
在△ABC和△DBE中,
AB=DB,
∠ABC=∠DBE,
CB=EB,
∴△ABC≌△DBE(SAS).
∴ ∠A=∠D.
1
A
2
C
B
D
E
解:DE=BF,DE//BF.理由如下:
在△ADE和△CBF中,
AD=CB,
∠DAC=∠BCA,
AE=CF,
∴ △ADE≌△CBF(SAS).
∴∠DEA=∠BFC,DE=BF.
∴∠DEC=∠BFE,DE//BF.
4.如图,已知AB=CD,BC=DA,E, F是AC上的两点,且AE=CF,写出DE和BF之间的关系,并证明你的结论.
A
B
D
E
F
C
同课章节目录
