人教版八年级数学上册第14章全等三角形14.3角的平分线第2课时角的平分线的判定 课件(共22张PPT)
文档属性
| 名称 | 人教版八年级数学上册第14章全等三角形14.3角的平分线第2课时角的平分线的判定 课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 668.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
1.理解角的平分线判定定理.
2.掌握角的平分线判定定理内容的证明方法并应用其解题.
3.会判断一个点是否在一个角的平分线上.
角的平分线判定定理内容的证明及应用.
角的平分线判定定理的理解.
难点
重点
O
D
P
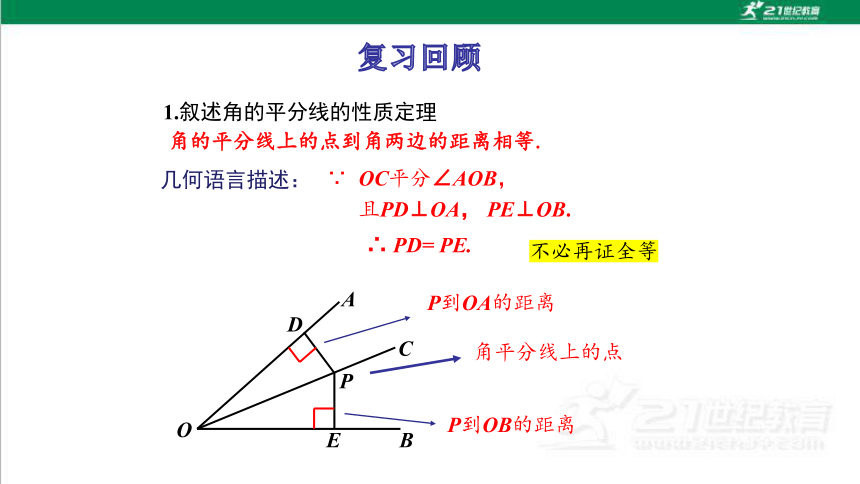
P到OA的距离
P到OB的距离
角平分线上的点
几何语言描述:
∵ OC平分∠AOB,
且PD⊥OA, PE⊥OB.
∴ PD= PE.
A
C
B
角的平分线上的点到角两边的距离相等.
1.叙述角的平分线的性质定理
不必再证全等
E
P
A
O
B
C
D
E
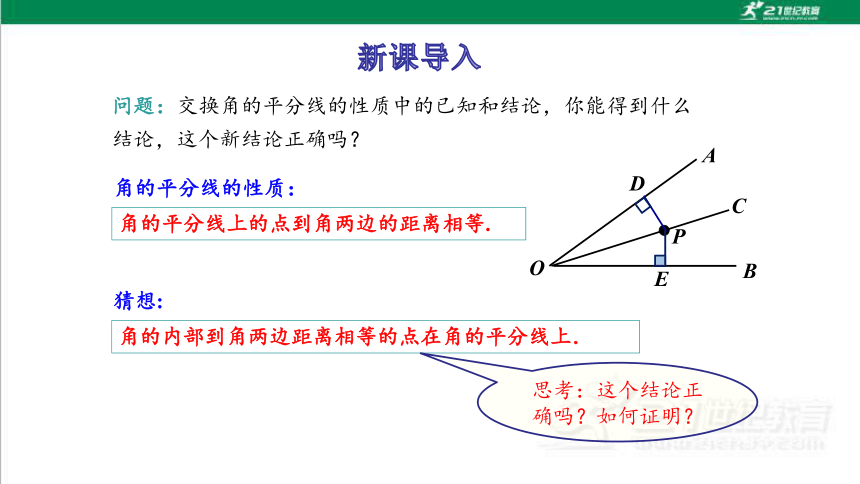
角的内部到角两边距离相等的点在角的平分线上.
问题:交换角的平分线的性质中的已知和结论,你能得到什么结论,这个新结论正确吗?
角的平分线的性质:
角的平分线上的点到角两边的距离相等.
猜想:
思考:这个结论正确吗?如何证明?
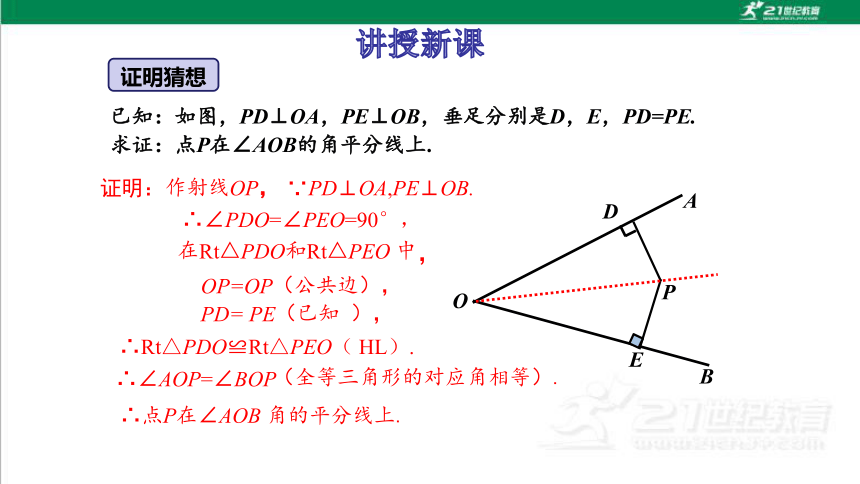
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D,E,PD=PE.求证:点P在∠AOB的角平分线上.
证明:
作射线OP,
∴点P在∠AOB 角的平分线上.
在Rt△PDO和Rt△PEO 中,
(全等三角形的对应角相等).
OP=OP(公共边),
PD= PE(已知 ),
B
A
D
O
P
E
∵PD⊥OA,PE⊥OB.
∴∠PDO=∠PEO=90°,
∴Rt△PDO≌Rt△PEO( HL).
∴∠AOP=∠BOP
证明猜想
判定定理:
角的内部到角两边距离相等的点在角的平分线上.
P
A
O
B
C
D
E
应用时所具备的条件:
(1)位置关系:点在角的内部;
(2)数量关系:该点到角两边距离相等.
定理的作用:判断点是否在角的平分线上.
应用格式:
∵ PD⊥OA,PE⊥OB,PD=PE,
∴点P 在∠AOB的平分线上.
知识点1 角的平分线的判定
1. 使用该判定定理的前提是这个点必须在角的内部.
2. 角的平分线的判定是由两个条件(垂线,线段相等) 得到一个结论( 角平分线).
3. 角的平分线的判定定理是证明两角相等的重要依据, 它比利用三角形全等证两角相等更快捷.
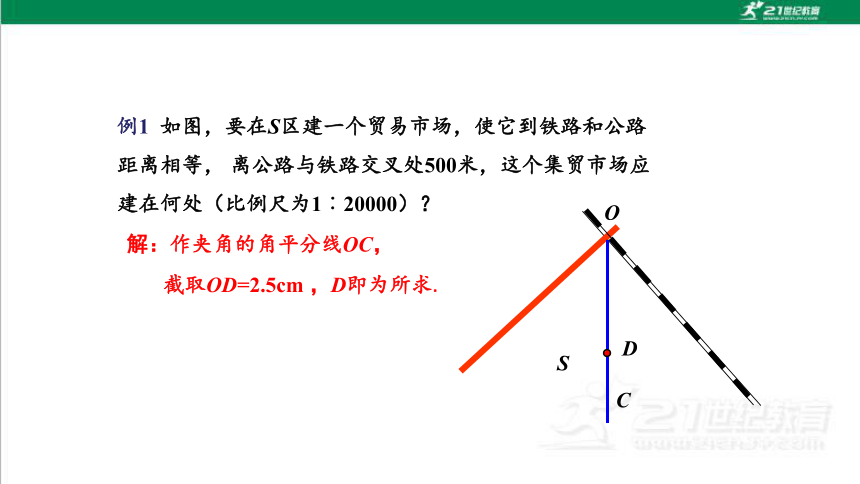
例1 如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500米,这个集贸市场应建在何处(比例尺为1︰20000)?
D
C
S
解:作夹角的角平分线OC,
截取OD=2.5cm ,D即为所求.
O
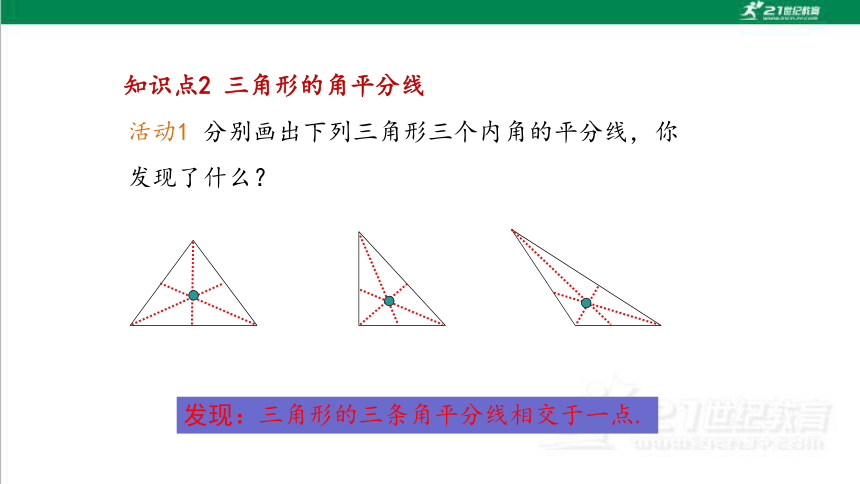
知识点2 三角形的角平分线
活动1 分别画出下列三角形三个内角的平分线,你发现了什么?
发现:三角形的三条角平分线相交于一点.
活动2 分别过交点作三角形三边的垂线,用刻度尺量一量,每组垂线段,你发现了什么?
发现:过交点作三角形三边的垂线段相等.
如何证明这个结论?
例2 已知:如图,△ABC的角平分线BM,CN相交于点P.
求证:
(1)点P到三边AB,BC,CA的距离相等.
(2)△ABC的三条角平分线交于一点.
A
B
C
P
N
M
D
E
F
证明:(1)过点P作PD⊥AB,PE⊥BC,PF⊥CA,垂足分别为D,E,F.
∵BM是△ABC的角平分线,
点P在BM上,
∴PD=PE.同理PE=PF.
∴PD=PE=PF.
即点P到三边AB,BC,CA的距离相等.
(2)由(1)得,点P到边AB,CA的距离相等,
∴点P在∠A的平分线上.
∴△ABC的三条角平分线交于一点.
A
B
C
P
N
M
结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等.
这个交点叫作三角形的内心.
M
E
N
A
B
C
P
O
D
变式1:如图,在Rt△ABC中,∠C=90°,AP平分∠BAC,BD平分∠ABC,AP,BD交于点O,过点O作OM⊥AC,若OM=4,
(1)求点O到△ABC三边的距离和.
温馨提示:不存在垂线段———构造应用
12
解:如图,连接OC.
M
E
N
A
B
C
P
O
D
(2)若△ABC的周长为32,求△ABC的面积.
角平分线
的判定定理
内容
角的内部到角两边距离相等的点在角的平分线上
作用
判断一个点是否在角的平分线上
结论
三角形的角平分线相交于内部一点
1.如图,P是△ABC外部一点,PD⊥AB,交AB的延长线于点D,PE⊥AC,交AC的延长线于点E,PF⊥BC于点F,且PD=PE=PF.关于点P有下列三种说法:
①点P在∠DBC的平分线上;
②点P在∠BCE的平分线上;
③点P在∠BAC的平分线上.
其中说法正确的个数为( )
A.0 B.1 C.2 D.3
D
C
A
E
B
D
F
P
┐
┐
2.如图,在CD上求一点P,使它到边OA,OB的距离相等, 则点P是( )
A.线段CD的中点
B.CD与过点O作CD的垂线的交点
C.CD与∠AOB的平分线的交点
D.以上均不对
C
3.如图,△ABC的三边AB,BC,CA的长分别为40,
50,60,其三条角平分线交于点O,则
S△ABO∶S△BCO∶S△CAO= ______________.
4 ∶5 ∶6
4. 如图,某个居民小区C附近有三条两两相交的道路MN,OA,OB,拟在MN上建造一个大型超市,使得它到OA,OB的距离相等,请确定该超市的位置P.
P
A
O
B
M
N
5. 如图所示,已知△ABC中,PE∥AB交BC于点E,PF∥AC交BC于点F,点P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.
解:AD平分∠BAC.理由如下:
∵D到PE的距离与到PF的距离相等,
∴点D在∠EPF的平分线上.
∴∠1=∠2.
又∵PE∥AB,∴∠1=∠3.
同理,∠2=∠4.
∴∠3=∠4,∴AD平分∠BAC.
A
B
C
E
F
D
(
(
(
(
3
4
1
2
P
6.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
证明:
过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M.
∵点F在∠BCE的平分线上, FG⊥AE, FM⊥BC.
∴FG=FM.
又∵点F在∠CBD的平分线上, FH⊥AD, FM⊥BC,
∴FM=FH,
∴FG=FH.
∴点F在∠DAE的平分线上.
G
H
M
A
B
C
F
E
D
1.理解角的平分线判定定理.
2.掌握角的平分线判定定理内容的证明方法并应用其解题.
3.会判断一个点是否在一个角的平分线上.
角的平分线判定定理内容的证明及应用.
角的平分线判定定理的理解.
难点
重点
O
D
P
P到OA的距离
P到OB的距离
角平分线上的点
几何语言描述:
∵ OC平分∠AOB,
且PD⊥OA, PE⊥OB.
∴ PD= PE.
A
C
B
角的平分线上的点到角两边的距离相等.
1.叙述角的平分线的性质定理
不必再证全等
E
P
A
O
B
C
D
E
角的内部到角两边距离相等的点在角的平分线上.
问题:交换角的平分线的性质中的已知和结论,你能得到什么结论,这个新结论正确吗?
角的平分线的性质:
角的平分线上的点到角两边的距离相等.
猜想:
思考:这个结论正确吗?如何证明?
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D,E,PD=PE.求证:点P在∠AOB的角平分线上.
证明:
作射线OP,
∴点P在∠AOB 角的平分线上.
在Rt△PDO和Rt△PEO 中,
(全等三角形的对应角相等).
OP=OP(公共边),
PD= PE(已知 ),
B
A
D
O
P
E
∵PD⊥OA,PE⊥OB.
∴∠PDO=∠PEO=90°,
∴Rt△PDO≌Rt△PEO( HL).
∴∠AOP=∠BOP
证明猜想
判定定理:
角的内部到角两边距离相等的点在角的平分线上.
P
A
O
B
C
D
E
应用时所具备的条件:
(1)位置关系:点在角的内部;
(2)数量关系:该点到角两边距离相等.
定理的作用:判断点是否在角的平分线上.
应用格式:
∵ PD⊥OA,PE⊥OB,PD=PE,
∴点P 在∠AOB的平分线上.
知识点1 角的平分线的判定
1. 使用该判定定理的前提是这个点必须在角的内部.
2. 角的平分线的判定是由两个条件(垂线,线段相等) 得到一个结论( 角平分线).
3. 角的平分线的判定定理是证明两角相等的重要依据, 它比利用三角形全等证两角相等更快捷.
例1 如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500米,这个集贸市场应建在何处(比例尺为1︰20000)?
D
C
S
解:作夹角的角平分线OC,
截取OD=2.5cm ,D即为所求.
O
知识点2 三角形的角平分线
活动1 分别画出下列三角形三个内角的平分线,你发现了什么?
发现:三角形的三条角平分线相交于一点.
活动2 分别过交点作三角形三边的垂线,用刻度尺量一量,每组垂线段,你发现了什么?
发现:过交点作三角形三边的垂线段相等.
如何证明这个结论?
例2 已知:如图,△ABC的角平分线BM,CN相交于点P.
求证:
(1)点P到三边AB,BC,CA的距离相等.
(2)△ABC的三条角平分线交于一点.
A
B
C
P
N
M
D
E
F
证明:(1)过点P作PD⊥AB,PE⊥BC,PF⊥CA,垂足分别为D,E,F.
∵BM是△ABC的角平分线,
点P在BM上,
∴PD=PE.同理PE=PF.
∴PD=PE=PF.
即点P到三边AB,BC,CA的距离相等.
(2)由(1)得,点P到边AB,CA的距离相等,
∴点P在∠A的平分线上.
∴△ABC的三条角平分线交于一点.
A
B
C
P
N
M
结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等.
这个交点叫作三角形的内心.
M
E
N
A
B
C
P
O
D
变式1:如图,在Rt△ABC中,∠C=90°,AP平分∠BAC,BD平分∠ABC,AP,BD交于点O,过点O作OM⊥AC,若OM=4,
(1)求点O到△ABC三边的距离和.
温馨提示:不存在垂线段———构造应用
12
解:如图,连接OC.
M
E
N
A
B
C
P
O
D
(2)若△ABC的周长为32,求△ABC的面积.
角平分线
的判定定理
内容
角的内部到角两边距离相等的点在角的平分线上
作用
判断一个点是否在角的平分线上
结论
三角形的角平分线相交于内部一点
1.如图,P是△ABC外部一点,PD⊥AB,交AB的延长线于点D,PE⊥AC,交AC的延长线于点E,PF⊥BC于点F,且PD=PE=PF.关于点P有下列三种说法:
①点P在∠DBC的平分线上;
②点P在∠BCE的平分线上;
③点P在∠BAC的平分线上.
其中说法正确的个数为( )
A.0 B.1 C.2 D.3
D
C
A
E
B
D
F
P
┐
┐
2.如图,在CD上求一点P,使它到边OA,OB的距离相等, 则点P是( )
A.线段CD的中点
B.CD与过点O作CD的垂线的交点
C.CD与∠AOB的平分线的交点
D.以上均不对
C
3.如图,△ABC的三边AB,BC,CA的长分别为40,
50,60,其三条角平分线交于点O,则
S△ABO∶S△BCO∶S△CAO= ______________.
4 ∶5 ∶6
4. 如图,某个居民小区C附近有三条两两相交的道路MN,OA,OB,拟在MN上建造一个大型超市,使得它到OA,OB的距离相等,请确定该超市的位置P.
P
A
O
B
M
N
5. 如图所示,已知△ABC中,PE∥AB交BC于点E,PF∥AC交BC于点F,点P是AD上一点,且点D到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.
解:AD平分∠BAC.理由如下:
∵D到PE的距离与到PF的距离相等,
∴点D在∠EPF的平分线上.
∴∠1=∠2.
又∵PE∥AB,∴∠1=∠3.
同理,∠2=∠4.
∴∠3=∠4,∴AD平分∠BAC.
A
B
C
E
F
D
(
(
(
(
3
4
1
2
P
6.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
证明:
过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M.
∵点F在∠BCE的平分线上, FG⊥AE, FM⊥BC.
∴FG=FM.
又∵点F在∠CBD的平分线上, FH⊥AD, FM⊥BC,
∴FM=FH,
∴FG=FH.
∴点F在∠DAE的平分线上.
G
H
M
A
B
C
F
E
D
同课章节目录
