6.2 组合与组合数 课件(共27张PPT)
文档属性
| 名称 | 6.2 组合与组合数 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
6.2.3 组合
第六章 计数原理
1.排列的定义:
一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列(arrangement).
我们把从n个不同元素中取出m(m≤n)个元素的所有不同排列的个数,叫做从n个不同元素中取出m个元素的排列数,用符号 表示.
2.排列数的定义:
3.排列数的计算:
(1)排列数公式(1):
(3)全排列数:
(2)排列数公式(2):
复习回顾
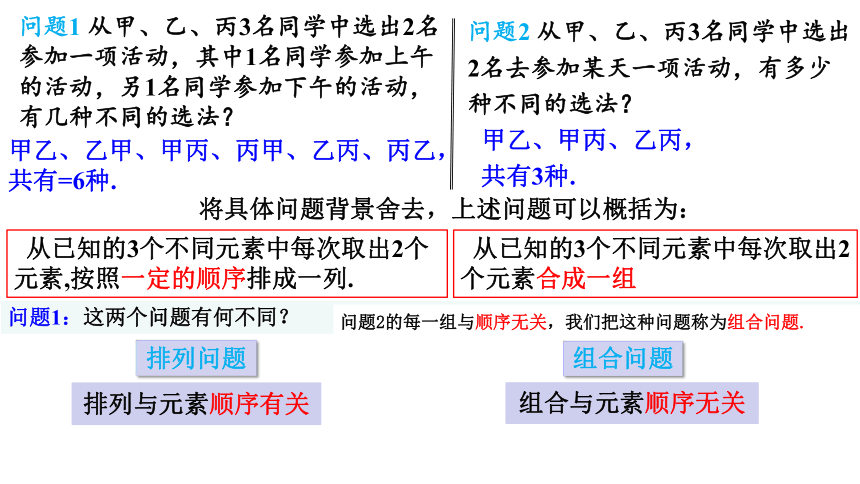
问题1:这两个问题有何不同?
甲乙、乙甲、甲丙、丙甲、乙丙、丙乙,
共有=6种.
甲乙、甲丙、乙丙,
共有3种.
问题2 从甲、乙、丙3名同学中选出2名去参加某天一项活动,有多少种不同的选法?
问题1 从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有几种不同的选法?
将具体问题背景舍去,上述问题可以概括为:
从已知的3个不同元素中每次取出2个元素,按照一定的顺序排成一列.
从已知的3个不同元素中每次取出2个元素合成一组
排列问题
组合问题
组合与元素顺序无关
排列与元素顺序有关
问题2的每一组与顺序无关,我们把这种问题称为组合问题.
一般地,从n个不同元素中取出m(m≤n)个元素作为一组,叫做从n个不同元素中取出m个元素的一个组合(combination).
1.组合定义:
注意:
(1)组合的特点:组合要求n个元素是不同的,取出的m个元素也是不同的,即从n个不同的元素中进行m次不放回地取出.
(2)组合的特性:元素的无序性. 取出的m个元素不讲究顺序,即元素没有位置的要求.
(互异性)
(无序性)
思考:你能说一说排列与组合之间的联系与区别吗?
一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从 n 个不 同元素中取出 m 个元素的一个排列.
组合定义:一般地,从n个不同元素中取出m(m≤n)个元素作为一组,叫做从n个不同元素中取出m个元素的一个组合.
排列定义:
排列、组合的联系与区别:
排列 组合
相同点 不同点
完成事情共分几步
从n个不同元素中取出m个元素
与元素的顺序有关
与元素的顺序无关
第一步、取
第二步、排
仅一步、取
组合
甲乙
甲丙
乙丙
甲乙,乙甲
甲丙,丙甲
乙丙,丙乙
排列
问题1和问题2中“排列”和“组合”的对应关系:
练习 判断下列各事件是排列问题还是组合问题.
从1,2,3,…,9这九个数字中任取3个,组成一个三位数,这样的三位数共有多少个?
(2) 从1,2,3,…,9这九个数字中任取3个,组成一个集合,这样的集合有多
少个?
(1)排列
(2) 组合
变式1 判断下列事件是排列问题还是组合问题.
(1) 从10个人里选3个代表去开会,有多少种选法?
(2) 从10个人里选出3个做不同学科的课代表,有多少种选法?
(3) 有10个车站,则这条铁路线上共需准备多少种车票
(4) 有10个车站,共需要多少种不同的票价?
(5) 设集合A={a,b,c,d,e},则集合A的子集中含有3个元素的有多少个?
(6) 3人去干5种不同的工作,每人干1种,有多少种分工方法?
(7) 把3本相同的书分给5个学生,每人最多得1本,有几种分配方法?
(8) 10人聚会,见面后每两人之间要握手相互问候, 共需握手多少次
(1)组合
(2) 排列
(3) 排列
(4)组合
(5)组合
(6) 排列
(7)组合
(8)组合
从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号 表示.
元素总数
取出元素数
m,n所满足的条件是:
(1) m∈N*,n∈N* ;
(2) m≤n .
例如,从3个不同元素中任取2个元素的组合数为
从4个不同元素中任取3个元素的组合数为
2.组合数的概念:
“一个组合” 是指“从n个不同元素中取出m(m≤n)个元素合成一组”,它不是一个数;
“组合数” 是指“从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数”,
它是一个正整数.
组合与组合数的区别:
典例分析
平面内有A,B,C,D共4个点.
(1) 以其中2个点为端点的有向线段共有多少条
(2) 以其中2个点为端点的线段共有多少条
分析: (1)确定一条有向线段,不仅要确定两个端点,还要考虑它们的顺序,是
排列问题;
(2)确定一条线段,只需确定两个端点,而不需考虑它们的顺序,是组合问题.
(1)一条有向线段的端点要分起点和端点,以平面内4个 点中的两个点为端点的有向线段的条数,就是从4个元素中取出2个元素的排列数,共有
条.
(2) 将(1)中端点相同、方向不同的2条有向线段作为1条线段,就是以平面内4个点中的2个点为端点的线段的条数, 共有如下6条:AB, AC, AD, BC, BD, CD.
思考:利用排列和组合之间的关系,以“元素相同”为标准分类,你能建立起例5(1)中排列和(2)中组合之间的对应关系吗?
进一步地,能否从这种对应关系出发,由排列数求出组合的个数
结论:取出2个元素的组合的个数是排列数的一半.
思考:校门口停放着9辆共享自行车,下面的问题是排列问题,还是组合问题
(1) 从中选3辆,有多少种不同的方法
(2) 从中选3辆给3位同学,有多少种不同的方法
解:
(1) 是组合问题,
(2) 是排列问题,不同的选法有
不同的选法有84种.
这里的n, m∈N*,并且m≤n,这个公式叫做组合数公式.
另外,我们规定
上面的公式还可以写成
3.组合数公式:
组合数公式的阶乘形式
典例分析
解:
计算:
4.组合数的性质:
性质1
证明:
性质2
4.组合数的性质:
课本P25
1. 计算:
课本P25
2. 求证:
典例分析
在100件产品中, 有98件合格品, 2件次品. 从这100件产品中任意抽出3件.
(1)有多少种不同的抽法
(2)抽出的3件中恰好有1件是次品的抽法有多少种
(3)抽出的3件中至少有1件是次品的抽法有多少种
(4)抽出的3件中至多有一件是次品的抽法有多少种
(1) 所有的不同抽法种数,就是从100件产品中抽出3件的组合数,所以抽法种数为
(2) 从2件次品中抽出1件的抽法有 种,从98件合格品中抽出2件的抽法有 种,因此抽出的3件中恰好有1件次品的抽法种数为
例7 在100件产品中, 有98件合格品, 2件次品. 从这100件产品中任意抽出3件.
(1)有多少种不同的抽法
(2)抽出的3件中恰好有1件是次品的抽法有多少种
典例分析
在100件产品中, 有98件合格品, 2件次品. 从这100件产品中任意抽出3件.
(3)抽出的3件中至少有1件是次品的抽法有多少种
(4)抽出的3件中至多有1件是次品的抽法有多少种
抽出的3 件中至少有1件是次品的抽法种数,就是从100件产品中抽出3件的抽法种数减去3件都是合格品的抽法种数,即
从100件产品抽出的3件中至少有1件是次品,包括有1件次品和有2件次品两种情况,因此根据分类加法计数原理,抽出的3件中至少有1件是次品的抽法种数为
典例分析
(3) 解1(直接法):
解2(间接法):
1.有限制条件的组合问题
在100件产品中, 有98件合格品, 2件次品. 从这100件产品中任意抽出3件.
(3)抽出的3件中至少有1件是次品的抽法有多少种
(4)抽出的3件中至多有1件是次品的抽法有多少种
典例分析
从100件产品抽出的3件中至多有1件是次品,包括有0件次品和有1件次品两种情况,因此根据分类加法计数原理,抽出的3件中至多有1件是次品的抽法种数为
(4) 解:
课本P25
3. 有政治、历史、地理、物理、化学、生物这6门学科的学业水平考试成
绩,现要从中选3门考试成绩.
(1) 共有多少种不同的选法
(2) 如果物理和化学恰有1门被选,那么共有多少种不同的选法
(3) 如果物理和化学至少有1门被选,那么共有多少种不同的选法
解:
1.有限制条件的组合问题
补充例题 课外活动小组共12人,其中男生7人、女生5人,并且男、女生各有一名队长.现从中选5人主持某项活动,依下列条件各有多少种选法?
(1)至少有一名队长当选;
(2)至多有两名女生当选;
(3)既要有队长,又要有女生当选.
典例分析
540
546
525
(1)甲、乙、丙三人必须当选;
(2)甲、乙、丙三人不能当选;
(3)甲必须当选,乙、丙不能当选;
(4)甲、乙、丙三人只有一人当选;
(5)甲、乙、丙三人至多2人当选;
(6)甲、乙、丙三人至少1人当选.
4.在一次数学竞赛中,某学校有12人通过了初试,学校要从中选出5人去参加市级培训,在下列条件下,有多少种不同的选法?
课堂练习
有5个男生和3个女生,从中选出4人担任4门不同学科的课代表,求分别符合下列条件的选法数:
(1)有女生但人数必须少于男生;
(2)某女生一定担任语文课代表;
(3)某男生必须包括在内,但不担任数学课代表.
2.先选(取)后排问题
720
210
630
有翻译人员11名,其中5名仅通英语、4名仅通法语,还有2名英、法语皆通.现欲从中选出8名,其中4名译英语,另外4名译法语,一共可列多少张不同的名单?
3.与几何有关的组合问题
5
2
4
(1)平面内有9个点,其中4个点在一条直线上,此外没有3个点在一条直线上,
过这9个点可确定多少条直线?可以作多少个三角形?
=31
(2)空间12个点,其中5个点共面,此外无任何4个点共面,这12个点可确定多
少个不同的平面?
+1=211
课堂练习
=80
6.2.3 组合
第六章 计数原理
1.排列的定义:
一般地,从n个不同元素中取出m(m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列(arrangement).
我们把从n个不同元素中取出m(m≤n)个元素的所有不同排列的个数,叫做从n个不同元素中取出m个元素的排列数,用符号 表示.
2.排列数的定义:
3.排列数的计算:
(1)排列数公式(1):
(3)全排列数:
(2)排列数公式(2):
复习回顾
问题1:这两个问题有何不同?
甲乙、乙甲、甲丙、丙甲、乙丙、丙乙,
共有=6种.
甲乙、甲丙、乙丙,
共有3种.
问题2 从甲、乙、丙3名同学中选出2名去参加某天一项活动,有多少种不同的选法?
问题1 从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有几种不同的选法?
将具体问题背景舍去,上述问题可以概括为:
从已知的3个不同元素中每次取出2个元素,按照一定的顺序排成一列.
从已知的3个不同元素中每次取出2个元素合成一组
排列问题
组合问题
组合与元素顺序无关
排列与元素顺序有关
问题2的每一组与顺序无关,我们把这种问题称为组合问题.
一般地,从n个不同元素中取出m(m≤n)个元素作为一组,叫做从n个不同元素中取出m个元素的一个组合(combination).
1.组合定义:
注意:
(1)组合的特点:组合要求n个元素是不同的,取出的m个元素也是不同的,即从n个不同的元素中进行m次不放回地取出.
(2)组合的特性:元素的无序性. 取出的m个元素不讲究顺序,即元素没有位置的要求.
(互异性)
(无序性)
思考:你能说一说排列与组合之间的联系与区别吗?
一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从 n 个不 同元素中取出 m 个元素的一个排列.
组合定义:一般地,从n个不同元素中取出m(m≤n)个元素作为一组,叫做从n个不同元素中取出m个元素的一个组合.
排列定义:
排列、组合的联系与区别:
排列 组合
相同点 不同点
完成事情共分几步
从n个不同元素中取出m个元素
与元素的顺序有关
与元素的顺序无关
第一步、取
第二步、排
仅一步、取
组合
甲乙
甲丙
乙丙
甲乙,乙甲
甲丙,丙甲
乙丙,丙乙
排列
问题1和问题2中“排列”和“组合”的对应关系:
练习 判断下列各事件是排列问题还是组合问题.
从1,2,3,…,9这九个数字中任取3个,组成一个三位数,这样的三位数共有多少个?
(2) 从1,2,3,…,9这九个数字中任取3个,组成一个集合,这样的集合有多
少个?
(1)排列
(2) 组合
变式1 判断下列事件是排列问题还是组合问题.
(1) 从10个人里选3个代表去开会,有多少种选法?
(2) 从10个人里选出3个做不同学科的课代表,有多少种选法?
(3) 有10个车站,则这条铁路线上共需准备多少种车票
(4) 有10个车站,共需要多少种不同的票价?
(5) 设集合A={a,b,c,d,e},则集合A的子集中含有3个元素的有多少个?
(6) 3人去干5种不同的工作,每人干1种,有多少种分工方法?
(7) 把3本相同的书分给5个学生,每人最多得1本,有几种分配方法?
(8) 10人聚会,见面后每两人之间要握手相互问候, 共需握手多少次
(1)组合
(2) 排列
(3) 排列
(4)组合
(5)组合
(6) 排列
(7)组合
(8)组合
从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号 表示.
元素总数
取出元素数
m,n所满足的条件是:
(1) m∈N*,n∈N* ;
(2) m≤n .
例如,从3个不同元素中任取2个元素的组合数为
从4个不同元素中任取3个元素的组合数为
2.组合数的概念:
“一个组合” 是指“从n个不同元素中取出m(m≤n)个元素合成一组”,它不是一个数;
“组合数” 是指“从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数”,
它是一个正整数.
组合与组合数的区别:
典例分析
平面内有A,B,C,D共4个点.
(1) 以其中2个点为端点的有向线段共有多少条
(2) 以其中2个点为端点的线段共有多少条
分析: (1)确定一条有向线段,不仅要确定两个端点,还要考虑它们的顺序,是
排列问题;
(2)确定一条线段,只需确定两个端点,而不需考虑它们的顺序,是组合问题.
(1)一条有向线段的端点要分起点和端点,以平面内4个 点中的两个点为端点的有向线段的条数,就是从4个元素中取出2个元素的排列数,共有
条.
(2) 将(1)中端点相同、方向不同的2条有向线段作为1条线段,就是以平面内4个点中的2个点为端点的线段的条数, 共有如下6条:AB, AC, AD, BC, BD, CD.
思考:利用排列和组合之间的关系,以“元素相同”为标准分类,你能建立起例5(1)中排列和(2)中组合之间的对应关系吗?
进一步地,能否从这种对应关系出发,由排列数求出组合的个数
结论:取出2个元素的组合的个数是排列数的一半.
思考:校门口停放着9辆共享自行车,下面的问题是排列问题,还是组合问题
(1) 从中选3辆,有多少种不同的方法
(2) 从中选3辆给3位同学,有多少种不同的方法
解:
(1) 是组合问题,
(2) 是排列问题,不同的选法有
不同的选法有84种.
这里的n, m∈N*,并且m≤n,这个公式叫做组合数公式.
另外,我们规定
上面的公式还可以写成
3.组合数公式:
组合数公式的阶乘形式
典例分析
解:
计算:
4.组合数的性质:
性质1
证明:
性质2
4.组合数的性质:
课本P25
1. 计算:
课本P25
2. 求证:
典例分析
在100件产品中, 有98件合格品, 2件次品. 从这100件产品中任意抽出3件.
(1)有多少种不同的抽法
(2)抽出的3件中恰好有1件是次品的抽法有多少种
(3)抽出的3件中至少有1件是次品的抽法有多少种
(4)抽出的3件中至多有一件是次品的抽法有多少种
(1) 所有的不同抽法种数,就是从100件产品中抽出3件的组合数,所以抽法种数为
(2) 从2件次品中抽出1件的抽法有 种,从98件合格品中抽出2件的抽法有 种,因此抽出的3件中恰好有1件次品的抽法种数为
例7 在100件产品中, 有98件合格品, 2件次品. 从这100件产品中任意抽出3件.
(1)有多少种不同的抽法
(2)抽出的3件中恰好有1件是次品的抽法有多少种
典例分析
在100件产品中, 有98件合格品, 2件次品. 从这100件产品中任意抽出3件.
(3)抽出的3件中至少有1件是次品的抽法有多少种
(4)抽出的3件中至多有1件是次品的抽法有多少种
抽出的3 件中至少有1件是次品的抽法种数,就是从100件产品中抽出3件的抽法种数减去3件都是合格品的抽法种数,即
从100件产品抽出的3件中至少有1件是次品,包括有1件次品和有2件次品两种情况,因此根据分类加法计数原理,抽出的3件中至少有1件是次品的抽法种数为
典例分析
(3) 解1(直接法):
解2(间接法):
1.有限制条件的组合问题
在100件产品中, 有98件合格品, 2件次品. 从这100件产品中任意抽出3件.
(3)抽出的3件中至少有1件是次品的抽法有多少种
(4)抽出的3件中至多有1件是次品的抽法有多少种
典例分析
从100件产品抽出的3件中至多有1件是次品,包括有0件次品和有1件次品两种情况,因此根据分类加法计数原理,抽出的3件中至多有1件是次品的抽法种数为
(4) 解:
课本P25
3. 有政治、历史、地理、物理、化学、生物这6门学科的学业水平考试成
绩,现要从中选3门考试成绩.
(1) 共有多少种不同的选法
(2) 如果物理和化学恰有1门被选,那么共有多少种不同的选法
(3) 如果物理和化学至少有1门被选,那么共有多少种不同的选法
解:
1.有限制条件的组合问题
补充例题 课外活动小组共12人,其中男生7人、女生5人,并且男、女生各有一名队长.现从中选5人主持某项活动,依下列条件各有多少种选法?
(1)至少有一名队长当选;
(2)至多有两名女生当选;
(3)既要有队长,又要有女生当选.
典例分析
540
546
525
(1)甲、乙、丙三人必须当选;
(2)甲、乙、丙三人不能当选;
(3)甲必须当选,乙、丙不能当选;
(4)甲、乙、丙三人只有一人当选;
(5)甲、乙、丙三人至多2人当选;
(6)甲、乙、丙三人至少1人当选.
4.在一次数学竞赛中,某学校有12人通过了初试,学校要从中选出5人去参加市级培训,在下列条件下,有多少种不同的选法?
课堂练习
有5个男生和3个女生,从中选出4人担任4门不同学科的课代表,求分别符合下列条件的选法数:
(1)有女生但人数必须少于男生;
(2)某女生一定担任语文课代表;
(3)某男生必须包括在内,但不担任数学课代表.
2.先选(取)后排问题
720
210
630
有翻译人员11名,其中5名仅通英语、4名仅通法语,还有2名英、法语皆通.现欲从中选出8名,其中4名译英语,另外4名译法语,一共可列多少张不同的名单?
3.与几何有关的组合问题
5
2
4
(1)平面内有9个点,其中4个点在一条直线上,此外没有3个点在一条直线上,
过这9个点可确定多少条直线?可以作多少个三角形?
=31
(2)空间12个点,其中5个点共面,此外无任何4个点共面,这12个点可确定多
少个不同的平面?
+1=211
课堂练习
=80
