2024-2025学年暑假复习模拟试卷(含解析)六年级下册数学(苏教版)
文档属性
| 名称 | 2024-2025学年暑假复习模拟试卷(含解析)六年级下册数学(苏教版) |  | |
| 格式 | docx | ||
| 文件大小 | 390.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 22:42:51 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024-2025学年暑假复习模拟试卷(试题)六年级下册数学(苏教版)
一、单选题
1.有等底等高的圆锥形和圆柱形容器各一个,将圆柱形容器装满水倒入圆锥形容器,当水全部倒完时,从圆锥形容器内溢出36.2 mL水。这时,圆锥形容器内有( )mL水。
A.36.2 B.54.3 C.18.1
2.王阿姨家的冰箱,冷藏箱的温度是﹢2℃,冷冻箱的温度是﹣4℃。这个冰箱的冷藏箱与冷冻箱的温度相差( )℃。
A.﹣4 B.2 C.6 D.4
3.为了支援香港抗击疫情,王叔叔准备捐出6箱口罩,口罩的外包装正方体纸箱棱长是10dm,将这些纸箱堆放到墙角处(如图),露在外面的面积是( )dm2。
A.1000 B.1200 C.1300 D.1500
4.暑假里,小辉和小乐一起去参加书法培训,小辉每8天去一次,小乐每6天去一次。8月1日他们同时参加培训后,( )他们会再次相遇。
A.8月9日 B.8月15日 C.8月24日 D.8月25日
5.下面各种关系中,成正比例关系的是( )
A.圆柱的底面积不变,它的体积与高
B.一批货物,运走的吨数与剩下的吨数
C.平行四边形的面积一定,它的底与对应的高
6.爸爸打算乘坐10:00起飞的飞机出差,机场规定,乘客必须提前半小时登机,爸爸最晚要在( )到达登机口。
A.9:30 B.10:05 C.10:30
7.红红从一楼上到三楼用了20秒,照这样计算,她从一楼到六楼要( )。
A.30秒 B.40秒 C.50秒 D.60秒
8.如图,甲摸到白球得1分,乙摸到黑球得1分,在( )箱中摸最公平.
A. B.
C. D.
二、判断题
9.圆锥的体积扩大到原来的3倍,它就变成了圆柱。( )
10.绕直角三角形的任意一条边所在的直线旋转一周都能得到一个圆锥。( )
11.一组不全相等的数的平均数比最大的数要小。( )
12.第一小组的10名学生称体重,最重的为45kg,最轻的为30kg。他们的平均体重可能是35kg。(
)
13.某商品原价200元,现在只花了七折的钱,现价为70元。(
)
14.周长相等的两个圆,面积也相等。( )
15.小维说:和 可以组成一个比例。( )
说理:( )。
16.如果10个零件中有一个次品(次品的质量轻一些),要保证找到次品,至少要称3次。( )
三、填空题
17.一件商品原价200元,现价160元,这件商品打了 折,现价比原价便宜了 %。
18.半径是6dm的半圆,它的周长是 dm ,面积是 dm2。
19.一个长方形的长和宽分别是24cm和9cm,至少用 个这样的长方形才能拼成一个正方形,这个正方形的面积是 cm2。
20.一个密封的长方体玻璃缸装有少量的水,玻璃缸的长宽高分别是40厘米、30厘米、25厘米,把玻璃缸不同的面作底摆放在桌面上,其中水面最低高度是5厘米,水面的高度最高是 厘米。
21.A、B两城的实际距离是40km,如果把它画在一幅比例尺是1:800000的地图上,要画 cm长。
22.(比例尺)在比例尺是1:30000000的地图上,量得甲地到乙地的距离是5.6厘米。一辆汽车按3:2的比例分两天跑完全程,两天跑的路程的差为 千米。
23.从时针指向4点开始,再经过 分钟时针正好与分针重合。
24.有1元、5元、10元的人民币共14张,共计66元,其中1元的比10元的多2张,则1元钞票有 张;5元钞票有 张;10元钞票有 张。
四、计算
25. 直接写得数。
0.6×1.2= 6.2÷0.2= 7.5÷0.25= 1.6×1.6÷1.6=
9÷1.5= 3.9÷1.3= 1.25×7×8= 1.8×0.5=
26.用竖式计算(得数保留两位小数)
(1)2.04×5.22≈
(2)0.926÷2.3≈
27.用你喜欢的方法计算下面各题。
28.解方程。
(1) (2)
五、操作题
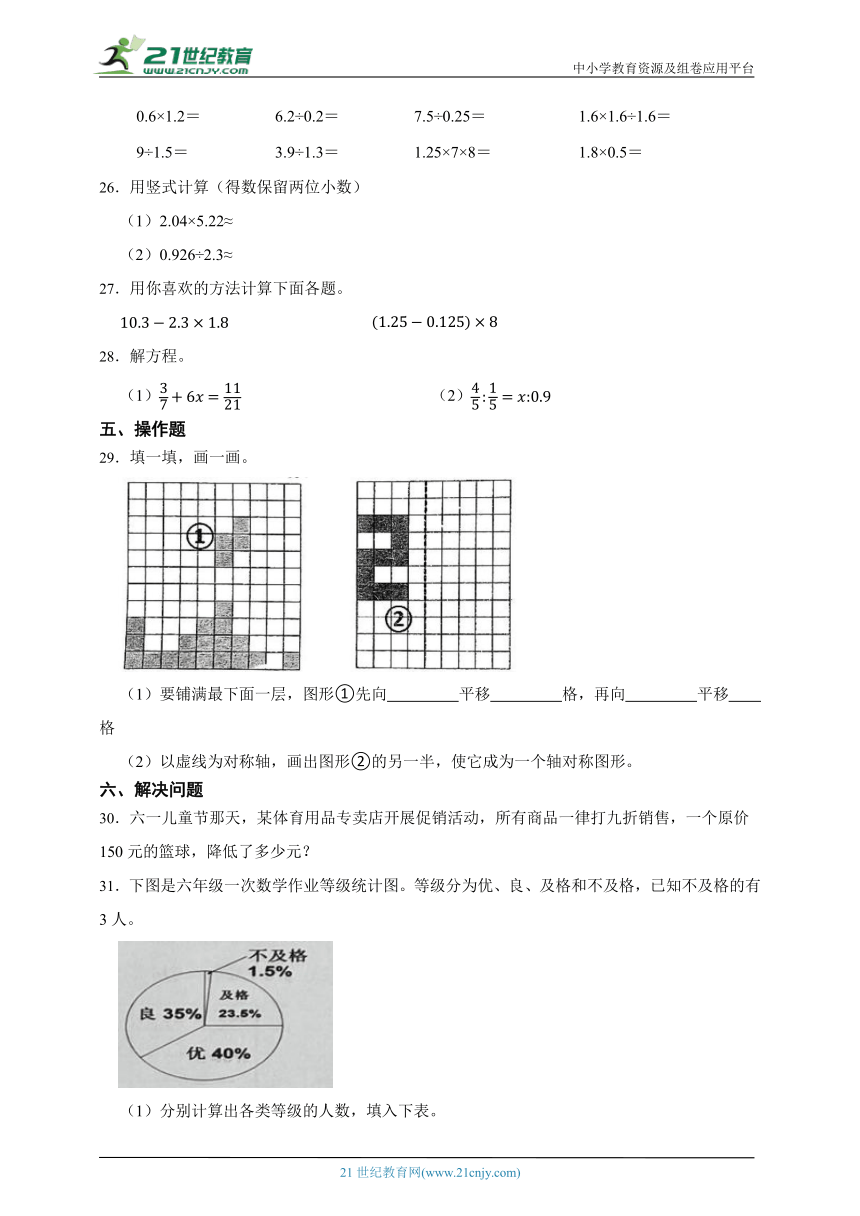
29.填一填,画一画。
(1)要铺满最下面一层,图形①先向 平移 格,再向 平移 格
(2)以虚线为对称轴,画出图形②的另一半,使它成为一个轴对称图形。
六、解决问题
30.六一儿童节那天,某体育用品专卖店开展促销活动,所有商品一律打九折销售,一个原价150元的篮球,降低了多少元?
31.下图是六年级一次数学作业等级统计图。等级分为优、良、及格和不及格,已知不及格的有3人。
(1)分别计算出各类等级的人数,填入下表。
等级 优 良 及格 不及格 合计
人数
(2)等级“良”的人数比等级“优”的人数少百分之几?
(3)请你根据六年级一次数学作业等级统计图提出数学问题并解答
32.一个圆锥形沙堆,底面周长是37.68m,高是5m,用这堆沙在10m宽的公路上铺5cm厚的路面,能铺多长?
33.亮亮爸爸打算自己用钢管制作一个长0.8米,宽0.5米,高1.5米的长方体简易挂衣柜的框架。至少需要多少米的钢管?如果给它做一个没有底面的布罩,至少需要用多少布?
34. 一块长方形的布,长18分米,宽12分米。要把它裁成正方形手绢(没有剩余),至少能裁多少块
35.为了更好地防控新冠疫情,学校每天都要进行消毒工作,84消毒液是常见的消毒剂,常用于地面、污染物表面的消毒。教室消毒常按原液和水1:99比例稀释,现需要把35毫升的消毒液稀释后给六一班的教室消毒,需要配多少毫升水?
36.怎样租船最划算?
37.向水中扔一块石子,水面上会激起一圈圈圆形波纹。假如波纹以0.5米/秒的速度向周围扩散,向水中扔进石子10秒钟后,水面泛起波纹的最大面积是多少?
答案解析部分
1.【答案】C
【解析】【解答】解:36.2÷2=18.1(mL)
故答案为:C。
【分析】 等底等高的圆柱体积是圆锥体积的3倍,等底等高的圆锥形和圆柱形容器各一个,将圆柱形容器装满水倒入圆锥形容器,当水全部倒完时,从圆锥形容器内溢出的水的体积是圆锥体积的2倍。
2.【答案】C
3.【答案】B
【解析】【解答】解:10×10×12
=100×12
=1200(平方分米)。
故答案为:B。
【分析】露在外面的面积=平均每个面的面积×露在外面的面的个数;其中,平均每个面的面积=棱长×棱长。
4.【答案】D
【解析】【解答】解:8和6的最小公倍数是24,所以他们24天后会再次相遇,即8月25日;
故答案为:D。
【分析】下次相遇的时间是8和6的最小公倍数,所以24+1=25,也就是8月25日。
5.【答案】A
【解析】【解答】解:A项:圆柱的体积÷高=圆柱的底面积(一定),圆柱的底面积不变,它的体积与高成正比例;
B项:一批货物,运走的吨数与剩下的吨数,不成比例;
C项:底×高=平行四边形的面积(一定),平行四边形的面积一定,它的底与对应的高成反比例。
故答案为:A。
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量;两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量。
6.【答案】A
【解析】【解答】解:半小时=30分
10时-30分=9时30分。
故答案为:A。
【分析】爸爸最晚到达登机口的时间=飞机起飞的时间-乘客登机提前的时间。
7.【答案】C
【解析】【解答】20÷(3-1)
=20÷2
=10(秒)
10×(6-1)
=10×5
=50(秒)
故答案为:C。
【分析】此题主要考查了植树问题的应用,先求出每上一层楼的时间,从一楼到三楼有(3-1)=2层,用除法求出每上一层用的时间,然后计算出从一楼到六楼需要的时间,据此列式解答。
8.【答案】B
【解析】【解答】解:从图中看出:B箱中黑球个数和白球个数相等,即可能性一样大;最公平;
故选:B.
【分析】A.白球3个,黑球2个,即摸到白球的可能性大,故不公平;
B.白球和黑球个数各占一半,可能性一样大,最公平;
C.白球2个,黑球4个,即摸到黑球的可能性大,故不公平;
D.白球3个,黑球4个,即摸到黑球的可能性大,故不公平.
9.【答案】错误
【解析】【解答】解:当圆锥和圆柱等底等高时,圆柱的体积是圆锥的3倍,但不能说圆锥的体积扩大到原来的3倍,它就变成了圆柱;
故答案为:错误。
【分析】圆柱的体积=底面积×高,圆锥的体积=×底面积×高。
10.【答案】错误
【解析】【解答】解:绕直角三角形的斜边所在直线旋转一周得到两个底面重合的圆锥;
故答案为:错误。
【分析】绕直角三角形的任意一条直角边所在的直线旋转一周都能得到一个圆锥。
11.【答案】正确
【解析】【解答】解:一组不全相等的数的平均数比最大的数要小。原题说法正确。
故答案为:正确。
【分析】平均数是一组数据的平均水平,一组不全相等的数的平均数比最大的数要小,比最小的数要大。
12.【答案】正确
【解析】【解答】解:第一小组的10名学生称体重,最重的为45kg,最轻的为30kg。他们的平均体重可能是35kg,原题干说法正确。
故答案为:正确。
【分析】平均数表示一组数据的平均水平,10名学生称体重,最重的为45kg,最轻的为30kg。他们的平均体重要在30kg到45kg之间,可能是35kg。
13.【答案】错误
【解析】【解答】解:200×70%=140元,所以现价为140元。
故答案为:错误。
【分析】现价=原价×打的折扣数,据此作答即可。
14.【答案】正确
【解析】【解答】解:周长相等的两个圆,面积也相等。
故答案为:正确。
【分析】周长相等的圆的半径相等,半径相等的圆的面积也相等。
15.【答案】√
因为 : 的比值相等,所以它们可以组成一个比例。
【解析】【解答】解:=
=
所以和 可以组成一个比例
故答案为:√,因为 : 的比值相等,所以它们可以组成一个比例。
【分析】表示两个比相等的式子叫做比例,所以只需计算题干给出的两个比的比值,然后看比值是否相等即可。
16.【答案】正确
【解析】【解答】解:把10个零件分为3个、3个、4个,共三组。
第一次:天平两端各放3个,如果平衡次品就在4个中;如果不平衡次品在上升那端的3个中;
第二次:如果次品在3个中,再称1次就能找出次品;如果在4个中,天平两端各放2个,上升那端的2个有一个是次品;
第三次:天平两端各放1个,上升那端的就是次品。
所以至少称3次。原题说法正确。
故答案为:正确。
【分析】找次品时把零件平均分成3份,如果不能平均分成3份,也要使第三份比另外两份少一个或多1个。这样一次就能把次品的范围缩小到最小。
17.【答案】八;20
【解析】【解答】解:160÷200=八折
(200-160)÷200
=40÷200
=20%。
故答案为:八;20。
【分析】这件商品打的折扣=现价÷原价;现价比原价便宜的钱数=(原价-现价) ÷原价。
18.【答案】30.84;56.52
【解析】【解答】解:(3.14+2)×6
=5.14×6
=30.84(分米)
3.14×62÷2
=113.04÷2
=56.52(平方分米)。
故答案为:30.84;56.52。
【分析】半圆的周长=π×半径+半径×2=(π+2)×半径;半圆的面积=π×半径2÷2。
19.【答案】24;5184
【解析】【解答】解:24=3×8;9=3×3;
24和9的最小公倍数是3×3×8=72;
(72÷24)×(72÷9)=3×8=24(个);
72×72=5184(平方厘米)。
故答案为:24;5184。
【分析】24和9的最小公倍数就是拼成的正方形的边长;(正方形的边长÷长方形的长)×(正方形的边长÷长方形的宽)=需要长方形的个数;正方形的边长×正方形的边长=正方形的面积。
20.【答案】8
【解析】【解答】解:水的体积:40×30×5=6000(立方厘米)
水的高度:6000÷(30×25)=8(厘米)
故答案为:8。
【分析】根据题意,要使水面最高,那么就要水体积最大时搭配最小的底面,当水的长为40厘米,宽为30厘米,高为5厘米时体积最大,30厘米和25厘米组成的底面积,据此解答。
21.【答案】5
【解析】【解答】解:40×100000×
=4000000×
=5(厘米)。
故答案为:5。
【分析】先单位换算40千米=4000000厘米,图上距离=实际距离×比例尺。
22.【答案】336
【解析】【解答】解:5.6÷=168000000(厘米)
168000000厘米=1680 千米
1680×=336(千米)
故答案为:336。
【分析】根据实际距离=图上距离÷比例尺计算出甲地到乙地的实际距离,再换算成以千米为单位;接着根据汽车按3:2的比例分两天跑完全程,可知两天跑的路程差为两天跑的路程和的,所以用两地的实际距离乘即可求出两天跑的路程差。
23.【答案】
【解析】【解答】解:时针1小时走1格,分针1小时走12格,从4点开始分针与时针重合所用的时间:
4÷(12-1)=(小时)=(分钟)
故答案为:
【分析】时钟指向4点即时针从12点走到4点共走了4个大格(1小时为一格),所以用4÷(12-1)即可求出经过的时间是多少小时,再换算成分钟即可.
24.【答案】6;4;4
【解析】【解答】把1元的减少2张,现在共有14-2=12(张),总钱数:66-2=64(元);
把1元的和10元的放在一起计算,每张平均面值:(1+10)÷2=5.5(元)
假设都是5元的,则1元的和10元的共有:
(64-12×5)÷(5.5-5)
=4÷0.5
=8(张)
10元的:8÷2=4(张)
1元的:4+2=6(张)
5元的:14-4-6=4(张)
故答案为:6;4;4
【分析】此题属于复杂的鸡兔同笼问题,可以把1元的减少2张,现在总张数是12张,总钱数是64元;然后把1元的与10元的放在一起计算,每张平均面值5..5元;然后运用假设法,假设都是5元的,计算出与64元相差的钱数,用相差的钱数除以(5.5-5)即可求出1元的和10元的共有的张数,除以2就是10元的张数,进而求出1元的和5元的张数即可.
25.【答案】
0.6×1.2=0.72 6.2÷0.2=31 7.5÷0.25=30 1.6×1.6÷1.6=1.6
9÷1.5=6 3.9÷1.3=3 1.25×7×8=70 1.8×0.5=0.9
【解析】【分析】小数乘法法则:先按照整数乘法的计算法则算出积,再看因数中共有几位小数,就从积的右边起数出几位,点上小数点;如果位数不够,就用“0”补足,注意:计算的结果,如果小数末尾有0的,根据小数的基本性质,在小数的末尾去掉零,小数的大小不变;
除数是小数的除法计算法则:先移动除数的小数点,使它变成整数,除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的补“0”),然后按照除数是整数的除法法则进行计算;
一个算式中,只有乘除法,按从左往右的顺序计算。
26.【答案】(1)2.04×5.22≈10.65;
(2)0.926÷2.3≈0.40;
【解析】【分析】小数乘法计算法则:先按照整数乘法的计算法则进行计算,再看因数中有几位小数,积的末尾就有几位小数。
除数是小数的计算方法:①移动除数的小数点,使它变成整数;②看除数原来有几位小数,就把被除数小数点向右移动相同的几位(位数不够时补0);③按照除数是整数的除法进行计算;④商的小数点与被除数的小数点对齐。
保留两位小数,即是对千分位上的数字四舍五入。
27.【答案】解:
【解析】【分析】小数乘法与加减的混合运算,先算乘法,再算加减法;
应用乘法分配律,括号里面的数分别与8相乘,再把所得的积相减。
28.【答案】(1);(2)
29.【答案】(1)右;3;下;6
(2)解:
【解析】【解答】解:(1)要铺满最下面一层,图形①先向右平移3格,再向下平移6格(答案不唯一)。
故答案为:(1)右;3;下;6。
【分析】(1)要铺满最下面一层,并且空格部分在右下角,就要向右、向下平移,然后数出平移的格数;
(2)画轴对称图形的方法是:数出或量出图形的关键点到对称轴的距离,在对称轴的另一侧找出关键点的对应点,按照所给图形的顺序连接各点。
30.【答案】解:150×(1-90%)
=150×10%
=15(元)
答:降低了15元。
【解析】【分析】篮球打折后降低的钱数=篮球的原价×(1-折扣)。
31.【答案】(1)解:如下表
等级 优 良 及格 不及格 合计
人数 80 70 47 3 200
(2)解:(80-70)÷80=12.5%
答: 等级“良”的人数比等级“优”的人数少12.5%。
(3)优和良的人数共多少?
解:80+70=150(人)
答:优和良的人数共有150人。
【解析】【解答】(1)总人数:3÷1.5%=200(人)
优:200×40%=80;良:200×35%=70;及格:200×23.5%=47;不及格:200×1.5%=3;合计:80+70+47+3=200
故答案为:
等级 优 良 及格 不及格 合计
人数 80 70 47 3 200
【分析】(1)由“不及格人数÷不及格占比”求总人数,再用“总人数×各等级占比”算对应人数;
(2)“(优人数-良人数)÷优人数”,计算得出良比优少的百分比;
(3)自问自答题型,建议提出简单问题解答,如:优和良的人数共多少?直接相加优、良人数即可。
32.【答案】解:5厘米=0.05米
37.68÷3.14÷2=6(米)
3.14×6×6×5÷3=565.2÷3=188.4(立方米)
188.4÷10÷0.05=376.8(米)
答:能铺376.8米。
【解析】【分析】圆锥的底面周长÷π÷2=底面半径,π×底面半径的平方×高÷3=圆锥的体积,
圆锥的体积÷长方体的宽÷长方体的高=长方体的长。
33.【答案】解:(0.8+0.5+1.5)×4
=2.8×4
=11.2(米)
(0.8×1.5+0.5×1.5)×2+0.8×0.5
=(1.2+0.75)×2+0.8×0.5
=1.95×2+0.8×0.5
=3.9+0.4
=4.3(平方米)
答:至少需要11.2米的钢管,如果给它做一个没有底面的布罩,至少需要用4.3平方米的布。
【解析】【分析】根据题意可知,钢管的长度就是长方体的棱长总和,长方体的棱长总和=(长+宽+高)×4;
如果给它做一个没有底面的布罩,需要的布的面积=(长×高+宽×高)×2+长×宽,据此列式解答。
34.【答案】解:
18和12的最大公因数是2×3=6
(18÷6)×(12÷6)
=3×2
=6(块)
答:至少能裁6块正方形手绢。
【解析】【分析】先用短除法求出18和12的最大公因数是2×3=6,至少能裁正方形手绢的块数=(长方形布的长÷18和12的最大公因数)×(长方形布的宽÷18和12的最大公因数)。
35.【答案】解:设需要配x毫升水。
35:x=1:99
x=35×99
x=3465
答:需要配3465毫升水。
【解析】【分析】比例关系:35毫升原液:水的容积=1:99,据此列比例;解比例时,根据比例的基本性质把比例化为方程,再根据等式性质解方程;比例的基本性质:比例的两个外项之积等于比例的两个内项之积。
36.【答案】解:①租9条大船,40×9=360(元);
②租8条大船,1条小船,
40×8+30
=320+30
=350(元)
③租7条大船,2条小船,
40×7+30×2
=280+60
=340(元)
360>350>340
答:租7条大船,2条小船最划算。
【解析】【分析】大船人均便宜,所以尽量租大船,先全部租大船,然后减少大船的条数,增加小船的条数,直到每条船刚好坐满,这样的租船方案是最省钱的。
37.【答案】解:0.5×10=5(米)
3.14×(5×5)
=3.14×25
=78.5(平方米)
答:水面泛起波纹的最大面积是78.5平方米。
【解析】【分析】水面泛起波纹的最大面积=π×半径×半径;其中,半径=波纹的速度×时间。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024-2025学年暑假复习模拟试卷(试题)六年级下册数学(苏教版)
一、单选题
1.有等底等高的圆锥形和圆柱形容器各一个,将圆柱形容器装满水倒入圆锥形容器,当水全部倒完时,从圆锥形容器内溢出36.2 mL水。这时,圆锥形容器内有( )mL水。
A.36.2 B.54.3 C.18.1
2.王阿姨家的冰箱,冷藏箱的温度是﹢2℃,冷冻箱的温度是﹣4℃。这个冰箱的冷藏箱与冷冻箱的温度相差( )℃。
A.﹣4 B.2 C.6 D.4
3.为了支援香港抗击疫情,王叔叔准备捐出6箱口罩,口罩的外包装正方体纸箱棱长是10dm,将这些纸箱堆放到墙角处(如图),露在外面的面积是( )dm2。
A.1000 B.1200 C.1300 D.1500
4.暑假里,小辉和小乐一起去参加书法培训,小辉每8天去一次,小乐每6天去一次。8月1日他们同时参加培训后,( )他们会再次相遇。
A.8月9日 B.8月15日 C.8月24日 D.8月25日
5.下面各种关系中,成正比例关系的是( )
A.圆柱的底面积不变,它的体积与高
B.一批货物,运走的吨数与剩下的吨数
C.平行四边形的面积一定,它的底与对应的高
6.爸爸打算乘坐10:00起飞的飞机出差,机场规定,乘客必须提前半小时登机,爸爸最晚要在( )到达登机口。
A.9:30 B.10:05 C.10:30
7.红红从一楼上到三楼用了20秒,照这样计算,她从一楼到六楼要( )。
A.30秒 B.40秒 C.50秒 D.60秒
8.如图,甲摸到白球得1分,乙摸到黑球得1分,在( )箱中摸最公平.
A. B.
C. D.
二、判断题
9.圆锥的体积扩大到原来的3倍,它就变成了圆柱。( )
10.绕直角三角形的任意一条边所在的直线旋转一周都能得到一个圆锥。( )
11.一组不全相等的数的平均数比最大的数要小。( )
12.第一小组的10名学生称体重,最重的为45kg,最轻的为30kg。他们的平均体重可能是35kg。(
)
13.某商品原价200元,现在只花了七折的钱,现价为70元。(
)
14.周长相等的两个圆,面积也相等。( )
15.小维说:和 可以组成一个比例。( )
说理:( )。
16.如果10个零件中有一个次品(次品的质量轻一些),要保证找到次品,至少要称3次。( )
三、填空题
17.一件商品原价200元,现价160元,这件商品打了 折,现价比原价便宜了 %。
18.半径是6dm的半圆,它的周长是 dm ,面积是 dm2。
19.一个长方形的长和宽分别是24cm和9cm,至少用 个这样的长方形才能拼成一个正方形,这个正方形的面积是 cm2。
20.一个密封的长方体玻璃缸装有少量的水,玻璃缸的长宽高分别是40厘米、30厘米、25厘米,把玻璃缸不同的面作底摆放在桌面上,其中水面最低高度是5厘米,水面的高度最高是 厘米。
21.A、B两城的实际距离是40km,如果把它画在一幅比例尺是1:800000的地图上,要画 cm长。
22.(比例尺)在比例尺是1:30000000的地图上,量得甲地到乙地的距离是5.6厘米。一辆汽车按3:2的比例分两天跑完全程,两天跑的路程的差为 千米。
23.从时针指向4点开始,再经过 分钟时针正好与分针重合。
24.有1元、5元、10元的人民币共14张,共计66元,其中1元的比10元的多2张,则1元钞票有 张;5元钞票有 张;10元钞票有 张。
四、计算
25. 直接写得数。
0.6×1.2= 6.2÷0.2= 7.5÷0.25= 1.6×1.6÷1.6=
9÷1.5= 3.9÷1.3= 1.25×7×8= 1.8×0.5=
26.用竖式计算(得数保留两位小数)
(1)2.04×5.22≈
(2)0.926÷2.3≈
27.用你喜欢的方法计算下面各题。
28.解方程。
(1) (2)
五、操作题
29.填一填,画一画。
(1)要铺满最下面一层,图形①先向 平移 格,再向 平移 格
(2)以虚线为对称轴,画出图形②的另一半,使它成为一个轴对称图形。
六、解决问题
30.六一儿童节那天,某体育用品专卖店开展促销活动,所有商品一律打九折销售,一个原价150元的篮球,降低了多少元?
31.下图是六年级一次数学作业等级统计图。等级分为优、良、及格和不及格,已知不及格的有3人。
(1)分别计算出各类等级的人数,填入下表。
等级 优 良 及格 不及格 合计
人数
(2)等级“良”的人数比等级“优”的人数少百分之几?
(3)请你根据六年级一次数学作业等级统计图提出数学问题并解答
32.一个圆锥形沙堆,底面周长是37.68m,高是5m,用这堆沙在10m宽的公路上铺5cm厚的路面,能铺多长?
33.亮亮爸爸打算自己用钢管制作一个长0.8米,宽0.5米,高1.5米的长方体简易挂衣柜的框架。至少需要多少米的钢管?如果给它做一个没有底面的布罩,至少需要用多少布?
34. 一块长方形的布,长18分米,宽12分米。要把它裁成正方形手绢(没有剩余),至少能裁多少块
35.为了更好地防控新冠疫情,学校每天都要进行消毒工作,84消毒液是常见的消毒剂,常用于地面、污染物表面的消毒。教室消毒常按原液和水1:99比例稀释,现需要把35毫升的消毒液稀释后给六一班的教室消毒,需要配多少毫升水?
36.怎样租船最划算?
37.向水中扔一块石子,水面上会激起一圈圈圆形波纹。假如波纹以0.5米/秒的速度向周围扩散,向水中扔进石子10秒钟后,水面泛起波纹的最大面积是多少?
答案解析部分
1.【答案】C
【解析】【解答】解:36.2÷2=18.1(mL)
故答案为:C。
【分析】 等底等高的圆柱体积是圆锥体积的3倍,等底等高的圆锥形和圆柱形容器各一个,将圆柱形容器装满水倒入圆锥形容器,当水全部倒完时,从圆锥形容器内溢出的水的体积是圆锥体积的2倍。
2.【答案】C
3.【答案】B
【解析】【解答】解:10×10×12
=100×12
=1200(平方分米)。
故答案为:B。
【分析】露在外面的面积=平均每个面的面积×露在外面的面的个数;其中,平均每个面的面积=棱长×棱长。
4.【答案】D
【解析】【解答】解:8和6的最小公倍数是24,所以他们24天后会再次相遇,即8月25日;
故答案为:D。
【分析】下次相遇的时间是8和6的最小公倍数,所以24+1=25,也就是8月25日。
5.【答案】A
【解析】【解答】解:A项:圆柱的体积÷高=圆柱的底面积(一定),圆柱的底面积不变,它的体积与高成正比例;
B项:一批货物,运走的吨数与剩下的吨数,不成比例;
C项:底×高=平行四边形的面积(一定),平行四边形的面积一定,它的底与对应的高成反比例。
故答案为:A。
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量;两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量。
6.【答案】A
【解析】【解答】解:半小时=30分
10时-30分=9时30分。
故答案为:A。
【分析】爸爸最晚到达登机口的时间=飞机起飞的时间-乘客登机提前的时间。
7.【答案】C
【解析】【解答】20÷(3-1)
=20÷2
=10(秒)
10×(6-1)
=10×5
=50(秒)
故答案为:C。
【分析】此题主要考查了植树问题的应用,先求出每上一层楼的时间,从一楼到三楼有(3-1)=2层,用除法求出每上一层用的时间,然后计算出从一楼到六楼需要的时间,据此列式解答。
8.【答案】B
【解析】【解答】解:从图中看出:B箱中黑球个数和白球个数相等,即可能性一样大;最公平;
故选:B.
【分析】A.白球3个,黑球2个,即摸到白球的可能性大,故不公平;
B.白球和黑球个数各占一半,可能性一样大,最公平;
C.白球2个,黑球4个,即摸到黑球的可能性大,故不公平;
D.白球3个,黑球4个,即摸到黑球的可能性大,故不公平.
9.【答案】错误
【解析】【解答】解:当圆锥和圆柱等底等高时,圆柱的体积是圆锥的3倍,但不能说圆锥的体积扩大到原来的3倍,它就变成了圆柱;
故答案为:错误。
【分析】圆柱的体积=底面积×高,圆锥的体积=×底面积×高。
10.【答案】错误
【解析】【解答】解:绕直角三角形的斜边所在直线旋转一周得到两个底面重合的圆锥;
故答案为:错误。
【分析】绕直角三角形的任意一条直角边所在的直线旋转一周都能得到一个圆锥。
11.【答案】正确
【解析】【解答】解:一组不全相等的数的平均数比最大的数要小。原题说法正确。
故答案为:正确。
【分析】平均数是一组数据的平均水平,一组不全相等的数的平均数比最大的数要小,比最小的数要大。
12.【答案】正确
【解析】【解答】解:第一小组的10名学生称体重,最重的为45kg,最轻的为30kg。他们的平均体重可能是35kg,原题干说法正确。
故答案为:正确。
【分析】平均数表示一组数据的平均水平,10名学生称体重,最重的为45kg,最轻的为30kg。他们的平均体重要在30kg到45kg之间,可能是35kg。
13.【答案】错误
【解析】【解答】解:200×70%=140元,所以现价为140元。
故答案为:错误。
【分析】现价=原价×打的折扣数,据此作答即可。
14.【答案】正确
【解析】【解答】解:周长相等的两个圆,面积也相等。
故答案为:正确。
【分析】周长相等的圆的半径相等,半径相等的圆的面积也相等。
15.【答案】√
因为 : 的比值相等,所以它们可以组成一个比例。
【解析】【解答】解:=
=
所以和 可以组成一个比例
故答案为:√,因为 : 的比值相等,所以它们可以组成一个比例。
【分析】表示两个比相等的式子叫做比例,所以只需计算题干给出的两个比的比值,然后看比值是否相等即可。
16.【答案】正确
【解析】【解答】解:把10个零件分为3个、3个、4个,共三组。
第一次:天平两端各放3个,如果平衡次品就在4个中;如果不平衡次品在上升那端的3个中;
第二次:如果次品在3个中,再称1次就能找出次品;如果在4个中,天平两端各放2个,上升那端的2个有一个是次品;
第三次:天平两端各放1个,上升那端的就是次品。
所以至少称3次。原题说法正确。
故答案为:正确。
【分析】找次品时把零件平均分成3份,如果不能平均分成3份,也要使第三份比另外两份少一个或多1个。这样一次就能把次品的范围缩小到最小。
17.【答案】八;20
【解析】【解答】解:160÷200=八折
(200-160)÷200
=40÷200
=20%。
故答案为:八;20。
【分析】这件商品打的折扣=现价÷原价;现价比原价便宜的钱数=(原价-现价) ÷原价。
18.【答案】30.84;56.52
【解析】【解答】解:(3.14+2)×6
=5.14×6
=30.84(分米)
3.14×62÷2
=113.04÷2
=56.52(平方分米)。
故答案为:30.84;56.52。
【分析】半圆的周长=π×半径+半径×2=(π+2)×半径;半圆的面积=π×半径2÷2。
19.【答案】24;5184
【解析】【解答】解:24=3×8;9=3×3;
24和9的最小公倍数是3×3×8=72;
(72÷24)×(72÷9)=3×8=24(个);
72×72=5184(平方厘米)。
故答案为:24;5184。
【分析】24和9的最小公倍数就是拼成的正方形的边长;(正方形的边长÷长方形的长)×(正方形的边长÷长方形的宽)=需要长方形的个数;正方形的边长×正方形的边长=正方形的面积。
20.【答案】8
【解析】【解答】解:水的体积:40×30×5=6000(立方厘米)
水的高度:6000÷(30×25)=8(厘米)
故答案为:8。
【分析】根据题意,要使水面最高,那么就要水体积最大时搭配最小的底面,当水的长为40厘米,宽为30厘米,高为5厘米时体积最大,30厘米和25厘米组成的底面积,据此解答。
21.【答案】5
【解析】【解答】解:40×100000×
=4000000×
=5(厘米)。
故答案为:5。
【分析】先单位换算40千米=4000000厘米,图上距离=实际距离×比例尺。
22.【答案】336
【解析】【解答】解:5.6÷=168000000(厘米)
168000000厘米=1680 千米
1680×=336(千米)
故答案为:336。
【分析】根据实际距离=图上距离÷比例尺计算出甲地到乙地的实际距离,再换算成以千米为单位;接着根据汽车按3:2的比例分两天跑完全程,可知两天跑的路程差为两天跑的路程和的,所以用两地的实际距离乘即可求出两天跑的路程差。
23.【答案】
【解析】【解答】解:时针1小时走1格,分针1小时走12格,从4点开始分针与时针重合所用的时间:
4÷(12-1)=(小时)=(分钟)
故答案为:
【分析】时钟指向4点即时针从12点走到4点共走了4个大格(1小时为一格),所以用4÷(12-1)即可求出经过的时间是多少小时,再换算成分钟即可.
24.【答案】6;4;4
【解析】【解答】把1元的减少2张,现在共有14-2=12(张),总钱数:66-2=64(元);
把1元的和10元的放在一起计算,每张平均面值:(1+10)÷2=5.5(元)
假设都是5元的,则1元的和10元的共有:
(64-12×5)÷(5.5-5)
=4÷0.5
=8(张)
10元的:8÷2=4(张)
1元的:4+2=6(张)
5元的:14-4-6=4(张)
故答案为:6;4;4
【分析】此题属于复杂的鸡兔同笼问题,可以把1元的减少2张,现在总张数是12张,总钱数是64元;然后把1元的与10元的放在一起计算,每张平均面值5..5元;然后运用假设法,假设都是5元的,计算出与64元相差的钱数,用相差的钱数除以(5.5-5)即可求出1元的和10元的共有的张数,除以2就是10元的张数,进而求出1元的和5元的张数即可.
25.【答案】
0.6×1.2=0.72 6.2÷0.2=31 7.5÷0.25=30 1.6×1.6÷1.6=1.6
9÷1.5=6 3.9÷1.3=3 1.25×7×8=70 1.8×0.5=0.9
【解析】【分析】小数乘法法则:先按照整数乘法的计算法则算出积,再看因数中共有几位小数,就从积的右边起数出几位,点上小数点;如果位数不够,就用“0”补足,注意:计算的结果,如果小数末尾有0的,根据小数的基本性质,在小数的末尾去掉零,小数的大小不变;
除数是小数的除法计算法则:先移动除数的小数点,使它变成整数,除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的补“0”),然后按照除数是整数的除法法则进行计算;
一个算式中,只有乘除法,按从左往右的顺序计算。
26.【答案】(1)2.04×5.22≈10.65;
(2)0.926÷2.3≈0.40;
【解析】【分析】小数乘法计算法则:先按照整数乘法的计算法则进行计算,再看因数中有几位小数,积的末尾就有几位小数。
除数是小数的计算方法:①移动除数的小数点,使它变成整数;②看除数原来有几位小数,就把被除数小数点向右移动相同的几位(位数不够时补0);③按照除数是整数的除法进行计算;④商的小数点与被除数的小数点对齐。
保留两位小数,即是对千分位上的数字四舍五入。
27.【答案】解:
【解析】【分析】小数乘法与加减的混合运算,先算乘法,再算加减法;
应用乘法分配律,括号里面的数分别与8相乘,再把所得的积相减。
28.【答案】(1);(2)
29.【答案】(1)右;3;下;6
(2)解:
【解析】【解答】解:(1)要铺满最下面一层,图形①先向右平移3格,再向下平移6格(答案不唯一)。
故答案为:(1)右;3;下;6。
【分析】(1)要铺满最下面一层,并且空格部分在右下角,就要向右、向下平移,然后数出平移的格数;
(2)画轴对称图形的方法是:数出或量出图形的关键点到对称轴的距离,在对称轴的另一侧找出关键点的对应点,按照所给图形的顺序连接各点。
30.【答案】解:150×(1-90%)
=150×10%
=15(元)
答:降低了15元。
【解析】【分析】篮球打折后降低的钱数=篮球的原价×(1-折扣)。
31.【答案】(1)解:如下表
等级 优 良 及格 不及格 合计
人数 80 70 47 3 200
(2)解:(80-70)÷80=12.5%
答: 等级“良”的人数比等级“优”的人数少12.5%。
(3)优和良的人数共多少?
解:80+70=150(人)
答:优和良的人数共有150人。
【解析】【解答】(1)总人数:3÷1.5%=200(人)
优:200×40%=80;良:200×35%=70;及格:200×23.5%=47;不及格:200×1.5%=3;合计:80+70+47+3=200
故答案为:
等级 优 良 及格 不及格 合计
人数 80 70 47 3 200
【分析】(1)由“不及格人数÷不及格占比”求总人数,再用“总人数×各等级占比”算对应人数;
(2)“(优人数-良人数)÷优人数”,计算得出良比优少的百分比;
(3)自问自答题型,建议提出简单问题解答,如:优和良的人数共多少?直接相加优、良人数即可。
32.【答案】解:5厘米=0.05米
37.68÷3.14÷2=6(米)
3.14×6×6×5÷3=565.2÷3=188.4(立方米)
188.4÷10÷0.05=376.8(米)
答:能铺376.8米。
【解析】【分析】圆锥的底面周长÷π÷2=底面半径,π×底面半径的平方×高÷3=圆锥的体积,
圆锥的体积÷长方体的宽÷长方体的高=长方体的长。
33.【答案】解:(0.8+0.5+1.5)×4
=2.8×4
=11.2(米)
(0.8×1.5+0.5×1.5)×2+0.8×0.5
=(1.2+0.75)×2+0.8×0.5
=1.95×2+0.8×0.5
=3.9+0.4
=4.3(平方米)
答:至少需要11.2米的钢管,如果给它做一个没有底面的布罩,至少需要用4.3平方米的布。
【解析】【分析】根据题意可知,钢管的长度就是长方体的棱长总和,长方体的棱长总和=(长+宽+高)×4;
如果给它做一个没有底面的布罩,需要的布的面积=(长×高+宽×高)×2+长×宽,据此列式解答。
34.【答案】解:
18和12的最大公因数是2×3=6
(18÷6)×(12÷6)
=3×2
=6(块)
答:至少能裁6块正方形手绢。
【解析】【分析】先用短除法求出18和12的最大公因数是2×3=6,至少能裁正方形手绢的块数=(长方形布的长÷18和12的最大公因数)×(长方形布的宽÷18和12的最大公因数)。
35.【答案】解:设需要配x毫升水。
35:x=1:99
x=35×99
x=3465
答:需要配3465毫升水。
【解析】【分析】比例关系:35毫升原液:水的容积=1:99,据此列比例;解比例时,根据比例的基本性质把比例化为方程,再根据等式性质解方程;比例的基本性质:比例的两个外项之积等于比例的两个内项之积。
36.【答案】解:①租9条大船,40×9=360(元);
②租8条大船,1条小船,
40×8+30
=320+30
=350(元)
③租7条大船,2条小船,
40×7+30×2
=280+60
=340(元)
360>350>340
答:租7条大船,2条小船最划算。
【解析】【分析】大船人均便宜,所以尽量租大船,先全部租大船,然后减少大船的条数,增加小船的条数,直到每条船刚好坐满,这样的租船方案是最省钱的。
37.【答案】解:0.5×10=5(米)
3.14×(5×5)
=3.14×25
=78.5(平方米)
答:水面泛起波纹的最大面积是78.5平方米。
【解析】【分析】水面泛起波纹的最大面积=π×半径×半径;其中,半径=波纹的速度×时间。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
