6.1 第1课时平均数与众数 教案(表格式)2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 6.1 第1课时平均数与众数 教案(表格式)2025-2026学年数学北师大版(2024)八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 129.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 00:00:00 | ||
图片预览


文档简介
第1课时 平均数与众数
课标摘录 1.理解平均数、众数的意义,能计算平均数、众数,知道它们是对数据集中趋势的描述。 2.能解释数据分析的结果,能根据结果作出简单的判断和预测,并能进行交流。 3.体会数据分析的重要性,形成数据观念,发展模型观念。
素养目标 1.理解算术平均数、众数的概念,会求一组数据的算术平均数和众数。 2.经历用平均数描述数据集中趋势的过程,发展数据分析观念。 3.通过使用平均数和众数解决实际问题,让学生体会数学与生活的密切联系。
教学重难点 重点:能求算术平均数和众数。 难点:能熟练求出一组数据的算术平均数和众数。
教学策略 为了帮助学生更好地理解概念、掌握计算方法并能够灵活应用,设计了以下教学策略。通过四人射击训练成绩引入概念,激发兴趣,利用图表、动画展示数据分布,帮助学生理解概念,该策略注重概念理解、实际应用和学生的主动参与,旨在提高教学效果。
情境导入 小松鼠对小马说:这条河平均水深1米,太危险了。小马说:我的身高已经长到1米5了,上一次都轻松过河了,这次就更没有问题了。 请问小马过河有危险吗
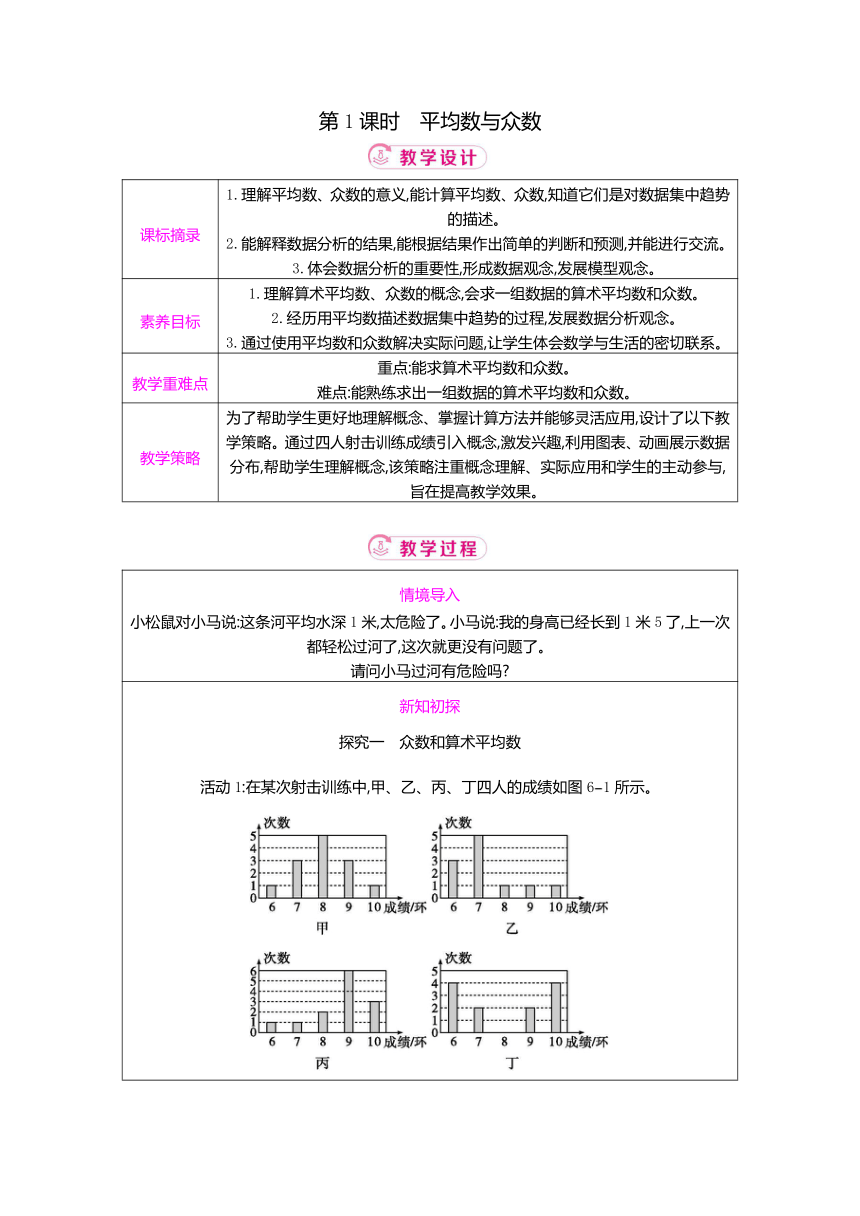
新知初探 探究一 众数和算术平均数 活动1:在某次射击训练中,甲、乙、丙、丁四人的成绩如图61所示。 图61
问题: (1)观察统计图,甲的哪个射击成绩出现次数最多 其他选手呢 (2)不计算,请你尝试判断谁的射击成绩最好。你是怎么判断的 (3)算一算,验证你的判断是否正确。 学生活动:学生先独立思考,计算出平均数,然后再小组交流。各小组之间竞争回答,答对的加分,给予鼓励。 预设学生答案:(1)甲8环射击成绩出现次数最多,乙7环射击成绩出现次数最多,丙9环射击成绩出现次数最多,丁6、10环射击成绩出现次数最多。 (2)观察统计图,丙的射击成绩中9环和10环的次数相对较多,且成绩分布相对集中在较高环数,所以初步判断丙的射击成绩最好。 (3)经过计算甲和丁的平均射击成绩是8环,乙的平均射击成绩小于8环,丙的平均射击成绩约为8.7环,所以丙的射击成绩最好。 归纳总结:一组数据中出现次数最多的那个数据叫作这组数据的众数(mode)。例如,甲射击成绩的众数是8环,丁射击成绩的众数是6环和10环。 一组数据中所有数据之和除以这组数据的个数,就得到这组数据的算术平均数(mean),简称平均数。平均数是刻画一组数据集中趋势的一项指标,反映了一组数据的“中心”。 一般地,对于n个数x1,x2,…,xn,我们把(x1+x2+…+xn)叫作这n个数的算术平均数,简称平均数,记为。 活动2:思考·交流 问题: (1)一组数据的平均数一定在这组数据中吗 (2)如果甲又射击一次,意外脱靶,成绩为0环,那么这时甲的平均成绩会发生什么变化 (3)在某些比赛评分时,常常去掉一个最高分和一个最低分,然后计算平均成绩,你能说说这样做的好处吗 与同伴进行交流。 预设学生答案: (1)一组数据的平均数不一定在这组数据中。 (2)甲的平均成绩会降低,因为加入了一个数值为0的极端值,拉低了整体的总和,在数据个数增加的情况下,平均成绩变小。 (3)去掉最高分和最低分能减少异常评分对最终成绩的过度影响,使成绩更能反映选手的真实水平。 意图说明 通过让学生分组探究,竞争回答问题,进一步探索出算术平均数的概念,激发学生的积极性,让学生体会算术平均数的现实意义。
探究二 平均数、众数的应用 活动3:某店铺一种商品10天的销售量及顾客对店铺的评分如图62和图63所示。 图62 图63 (1)请你计算这种商品10天的平均销售量。 (2)顾客对店铺评分的众数是多少 顾客对店铺评分的平均数呢 解:(1)根据平均数计算公式可得: (121+138+156+148+152+141+128+130+125+122)÷10=136.1(件) 所以,这种商品10天的平均销售量是136.1件。 (2)从图63可知,评分为3分的人数为836人,占比83.6 %,人数最多。所以,顾客对店铺评分的众数是3分。 由图63可知,评1分的有10人,评2分的有32人,评3分的有836人,评4分的有101人,评5分的有21人。总人数为10+32+836+101+21=1 000(人),根据算术平均数公式可得: (1×10+2×32+3×836+4×101+5×21)÷1 000 =(10+64+2 508+404+105)÷1 000 =3 091÷1 000 =3.091(分) 所以,顾客对店铺评分的平均数是3.091分。 活动4:回顾·反思 从统计图中获取众数、平均数,你有哪些经验 意图说明 让学生理解众数和算术平均数的概念,能熟练计算出一组数据的众数和算术平均数,探究众数和算术平均数在实际生活中的应用。
当堂达标
课堂小结
板书设计 平均数与众数 1.众数的概念 2.算术平均数的概念 3.算术平均数的计算
教学反思
课标摘录 1.理解平均数、众数的意义,能计算平均数、众数,知道它们是对数据集中趋势的描述。 2.能解释数据分析的结果,能根据结果作出简单的判断和预测,并能进行交流。 3.体会数据分析的重要性,形成数据观念,发展模型观念。
素养目标 1.理解算术平均数、众数的概念,会求一组数据的算术平均数和众数。 2.经历用平均数描述数据集中趋势的过程,发展数据分析观念。 3.通过使用平均数和众数解决实际问题,让学生体会数学与生活的密切联系。
教学重难点 重点:能求算术平均数和众数。 难点:能熟练求出一组数据的算术平均数和众数。
教学策略 为了帮助学生更好地理解概念、掌握计算方法并能够灵活应用,设计了以下教学策略。通过四人射击训练成绩引入概念,激发兴趣,利用图表、动画展示数据分布,帮助学生理解概念,该策略注重概念理解、实际应用和学生的主动参与,旨在提高教学效果。
情境导入 小松鼠对小马说:这条河平均水深1米,太危险了。小马说:我的身高已经长到1米5了,上一次都轻松过河了,这次就更没有问题了。 请问小马过河有危险吗
新知初探 探究一 众数和算术平均数 活动1:在某次射击训练中,甲、乙、丙、丁四人的成绩如图61所示。 图61
问题: (1)观察统计图,甲的哪个射击成绩出现次数最多 其他选手呢 (2)不计算,请你尝试判断谁的射击成绩最好。你是怎么判断的 (3)算一算,验证你的判断是否正确。 学生活动:学生先独立思考,计算出平均数,然后再小组交流。各小组之间竞争回答,答对的加分,给予鼓励。 预设学生答案:(1)甲8环射击成绩出现次数最多,乙7环射击成绩出现次数最多,丙9环射击成绩出现次数最多,丁6、10环射击成绩出现次数最多。 (2)观察统计图,丙的射击成绩中9环和10环的次数相对较多,且成绩分布相对集中在较高环数,所以初步判断丙的射击成绩最好。 (3)经过计算甲和丁的平均射击成绩是8环,乙的平均射击成绩小于8环,丙的平均射击成绩约为8.7环,所以丙的射击成绩最好。 归纳总结:一组数据中出现次数最多的那个数据叫作这组数据的众数(mode)。例如,甲射击成绩的众数是8环,丁射击成绩的众数是6环和10环。 一组数据中所有数据之和除以这组数据的个数,就得到这组数据的算术平均数(mean),简称平均数。平均数是刻画一组数据集中趋势的一项指标,反映了一组数据的“中心”。 一般地,对于n个数x1,x2,…,xn,我们把(x1+x2+…+xn)叫作这n个数的算术平均数,简称平均数,记为。 活动2:思考·交流 问题: (1)一组数据的平均数一定在这组数据中吗 (2)如果甲又射击一次,意外脱靶,成绩为0环,那么这时甲的平均成绩会发生什么变化 (3)在某些比赛评分时,常常去掉一个最高分和一个最低分,然后计算平均成绩,你能说说这样做的好处吗 与同伴进行交流。 预设学生答案: (1)一组数据的平均数不一定在这组数据中。 (2)甲的平均成绩会降低,因为加入了一个数值为0的极端值,拉低了整体的总和,在数据个数增加的情况下,平均成绩变小。 (3)去掉最高分和最低分能减少异常评分对最终成绩的过度影响,使成绩更能反映选手的真实水平。 意图说明 通过让学生分组探究,竞争回答问题,进一步探索出算术平均数的概念,激发学生的积极性,让学生体会算术平均数的现实意义。
探究二 平均数、众数的应用 活动3:某店铺一种商品10天的销售量及顾客对店铺的评分如图62和图63所示。 图62 图63 (1)请你计算这种商品10天的平均销售量。 (2)顾客对店铺评分的众数是多少 顾客对店铺评分的平均数呢 解:(1)根据平均数计算公式可得: (121+138+156+148+152+141+128+130+125+122)÷10=136.1(件) 所以,这种商品10天的平均销售量是136.1件。 (2)从图63可知,评分为3分的人数为836人,占比83.6 %,人数最多。所以,顾客对店铺评分的众数是3分。 由图63可知,评1分的有10人,评2分的有32人,评3分的有836人,评4分的有101人,评5分的有21人。总人数为10+32+836+101+21=1 000(人),根据算术平均数公式可得: (1×10+2×32+3×836+4×101+5×21)÷1 000 =(10+64+2 508+404+105)÷1 000 =3 091÷1 000 =3.091(分) 所以,顾客对店铺评分的平均数是3.091分。 活动4:回顾·反思 从统计图中获取众数、平均数,你有哪些经验 意图说明 让学生理解众数和算术平均数的概念,能熟练计算出一组数据的众数和算术平均数,探究众数和算术平均数在实际生活中的应用。
当堂达标
课堂小结
板书设计 平均数与众数 1.众数的概念 2.算术平均数的概念 3.算术平均数的计算
教学反思
同课章节目录
